期末经典题型检测卷-2023-2024学年数学九年级上册苏科版(含解析)
文档属性
| 名称 | 期末经典题型检测卷-2023-2024学年数学九年级上册苏科版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末经典题型检测卷-2023-2024学年数学九年级上册苏科版
一、单选题
1.下列方程一定是一元二次方程的是( )
A. B.
C. D.
2.若关于x的一元二次方程的一个根是,则m的值为( )
A. B.1 C. D.2
3.在一次体育测试中,嘉琪所在小组人的成绩分别是:,,,,..则这人体育测试成绩的中位数是( )
A.47 B.48 C. D.49
4.下列命题中,真命题的个数是( )
①圆的每一条直径都是它的对称轴;②平分弦的直径必定垂直于这条弦;③在同圆或等圆中,相等的圆心角所对的弧相等;④在同圆中,相等的弦所对的弧相等.
A.4个 B.3个 C.2个 D.1个
5.参加足球联赛的每两队之间都进行两场比赛,共要比赛场,设共有个队参加比赛,则下列方程符合题意的是( )
A. B.
C. D.
6.如图,是的直径,垂直于弦于点D,的延长线交于点E.若,,则的长是( )
A.1 B. C.2 D.4
7.如图,在中,弦的长,圆心到的距离是,那么的半径是( )
A. B. C. D.
8.如图,、、是上的三点,并且,点是圆上的一个动点点不与点、、重合,连接、,则的度数是( )
A. B. C.或 D.或
二、填空题
9.一元二次方程的根的情况是 .
10.若圆锥的底面圆半径为2,母线长为5,则该圆锥的侧面积是 .
11.圆周率是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对有过深入的研究.目前,超级计算机已计算出的小数部分超过31.4万亿位.有学者发现,这10个数字出现的频率趋于稳定接近相同,从的小数部分随机取出一个数字,估计数字是6的概率为 .
12.已知关于x的一元二次方程的两根为,则 .
13.在方差计算公式中,可以看出的值为 .
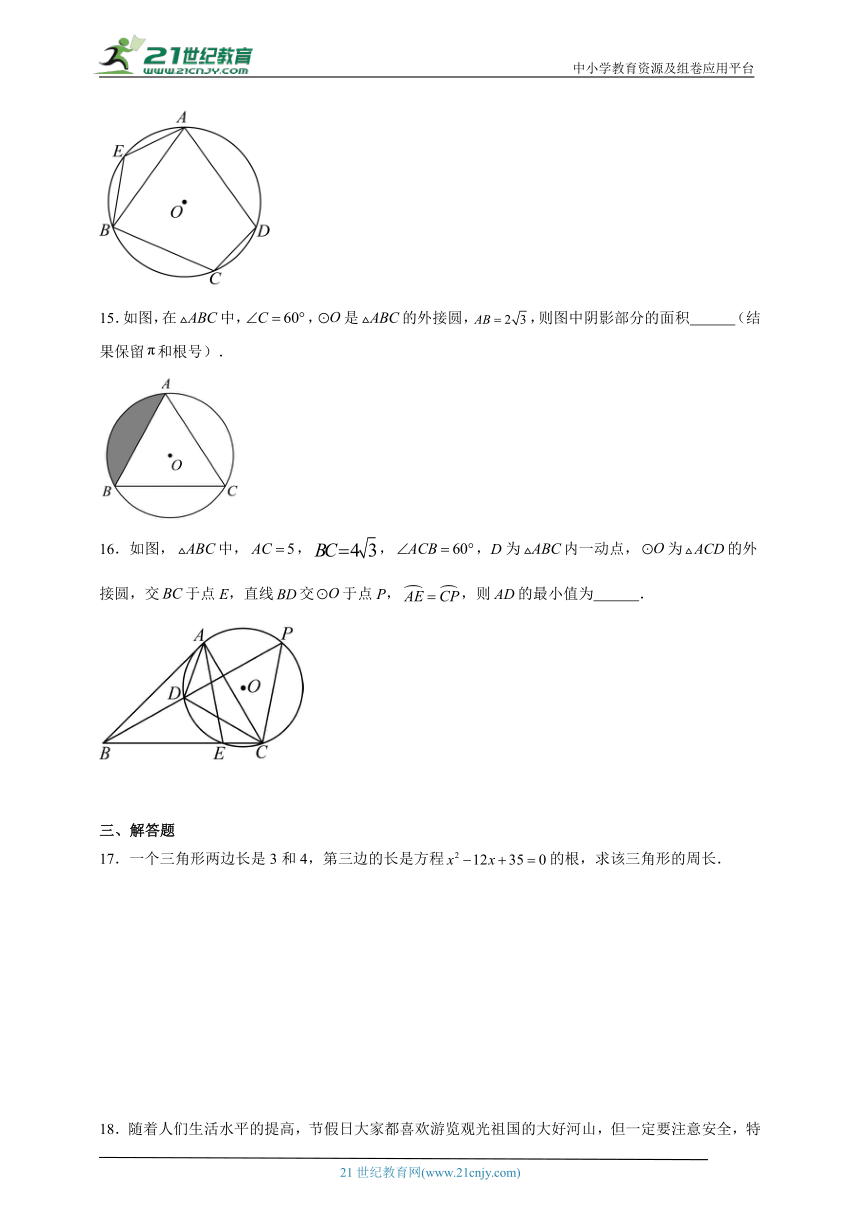
14.如图,在的内接四边形中,,点E在上,则 .
15.如图,在中,,是的外接圆,,则图中阴影部分的面积 (结果保留和根号).
16.如图,中,,,,D为内一动点,为的外接圆,交于点E,直线交于点P,,则的最小值为 .
三、解答题
17.一个三角形两边长是3和4,第三边的长是方程的根,求该三角形的周长.
18.随着人们生活水平的提高,节假日大家都喜欢游览观光祖国的大好河山,但一定要注意安全,特别要防止病毒的传染.我们利用学过的数学知识来解决一个关于病毒传染的问题:一个游客在旅游时,因不意防范,患上了流感,回家后,经两轮传染后有81人患上了流感,那么平均一个人传染了几个人?经过三轮传染后共有多少人患上了流感?
19.某餐饮店开拓线上团购业务,于今年五月底上线团购券,六月份销售了256张,七、八月份该团购券十分畅销,销售量持续走高,在售价不变的基础上,八月份的销售量达到400张,求七、八月份该团购券销售量的月平均增长率.
20.广州的白云山、越秀山、莲花山和大夫山被誉为广州四大名山,不仅风景秀美而且有丰厚的历史底蕴,是广州市民喜欢游玩之地.小明、小丽两家人决定周末去游玩,并用抽卡片的方式从白云山、越秀山、莲花山和大夫山(分别记为、、、)选出一个景点.他们准备了张不透明的卡片,正面分别写上、、和.卡片除正面字母不同外其余均相同.
(1)小明随机抽取一张卡片,则抽取到卡片的概率是_______;
(2)小明随机抽取一张卡片后,放回洗匀,小丽再随机抽取一张卡片,请用列或画树状图的方法求他们都抽取到同一地点的概率.
21.如图,在平面直角坐标系中,的三个顶点的坐标分别为,,.将绕点顺时针旋转,得到,
(1)画出,并直接写出点的坐标为 .
(2)求出旋转过程中边扫过的面积.
22.如图,在中,,以为直径的交于点,,垂足为.
(1)求证:是的切线;
(2)若,,求的长.
23.如图①,点、、在上,且,是弧上的一点,(点不与点、重合),连接、、,在上截取,连接.若,解答下列问题:
(1)求证:是等边三角形;
(2)求证:是等边三角形;
(3)如图②,若点和圆心重合,,则的长为 .
参考答案:
1.C
【分析】本题主要考查了一元二次方程的定义;只含有一个未知数,且未知数的最高次数是2的整式方程叫做一元二次方程.一元二次方程有三个特点:只含有一个未知数;未知数的最高次数是2;是整式方程.
【详解】解:A. 是二元一次方程,故本选项不符合题意;
B. 当时,不是一元二次方程,故本选项不符合题意;
C. 是一元二次方程,故本选项符合题意
D. 是分式方程,故本选项不符合题意;
故选:C.
2.B
【分析】根据一元二次方程的根的定义把方程根代入,得到关于m的方程,解方程即可得到m的值.此题考查了一元二次方程,熟练掌握一元二次方程根的定义是解题的关键.
【详解】解:∵关于x的一元二次方程的一个根是,
∴,
解得,
故选:B
3.B
【分析】本题考查了中位数的知识,解答本题的关键是掌握中位数的定义,注意在求解前观察:数据是否按大小顺序排列.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数,由此计算即可.
【详解】解:将这组数据从小到大排序后,这组数据的中间两个数为,,
这组数据的中位数为.
故选:B.
4.D
【分析】本题考查判断命题的真假,圆的对称性,垂径定理,圆周角定理.掌握相关知识点,是解题的关键.
【详解】解:①圆的每一条直径所在的直线都是它的对称轴;故①是假命题;
②平分弦(不是直径)的直径必定垂直于这条弦;故②是假命题;
③在同圆或等圆中,相等的圆心角所对的弧相等;故③是真命题;
④在同圆中,一弦对两弧,所以相等的弦所对的弧不一定相等,故④是假命题;
故选D.
5.D
【分析】本题考查了一元二次方程的应用,熟练掌握每两队之间都进行两场比赛的意义是解题的关键.
【详解】根据题意,得,
故选D.
6.C
【分析】本题主要考查了垂径定理,勾股定理,圆周角定理,由垂径定理得到,设,则,由勾股定理得,解方程求出,由是的直径,得到,,则.
【详解】解:∵,
∴,,
设,则,
在中,由勾股定理得,
∴,
解得,
∵是的直径,
∴,
∴,
故选C.
7.B
【分析】本题考查了勾股定理与垂径定理;根据图形可得,在中,勾股定理,即可求解.
【详解】解:∵弦的长,圆心到的距离是,
∴,
在中,,
故选:B.
8.D
【分析】本题考查了圆周角定理,圆内接四边形对角互补;根据同弧所对的圆周角相等以及圆内接四边形对角互补即可求解.
【详解】解:如图所示,
当在上时,,
当在上时,,
故选:D.
9.有两个不相等的实数根
【分析】此题考查了一元二次方程根的判别式.求根的判别式,进而得出答案.
【详解】解:∵,
∴一元二次方程有两个不相等的实数根
故答案为:有两个不相等的实数根.
10.
【分析】此题主要考查了圆锥侧面积公式,根据圆锥的底面半径为2,母线长为5,直接利用圆锥的侧面积公式求出它的侧面积即可.
【详解】解:根据圆锥侧面积公式:,
故答案为:.
11.
【分析】本题考查了利用频率估计概率,掌握大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率是解题的关键.
从的小数部分随机取出一个数字共有10种等可能的结果,其中出现数字6的只有1种结果,利用概率公式求解即可.
【详解】解:∵随着小数部分位数的增加,这10个数字出现的频率趋于稳定接近相同,
∴从的小数部分随机取出一个数字共有10种等可能的结果,其中出现数字2的只有1种结果,
∴P(数字是6).
故答案为:.
12.
【分析】本题主要考查了一元二次方程根与系数的关系,对于一元二次方程,若是该方程的两个实数根,则,据此求出,再代值计算即可.
【详解】解:∵关于x的一元二次方程的两根为,
∴,
∴,
故答案为:.
13.
【分析】本题考查了方差与平均数的计算,由方差的计算可得这组数据的平均数,然后利用平均数的计算方法即可求解,掌握方差的计算公式是解题的关键.
【详解】解:由题意可得,这组数据共个数,且它们的平均数是,
∴,
故答案为:.
14.126
【分析】本题考查了圆内接四边形的性质:圆内接四边形的对角互补.等腰三角形的性质和三角形内角和定理.先根据圆内接四边形的性质计算出,再根据等腰三角形的性质和三角形内角和定理计算出,然后再根据圆内接四边形的性质可得的度数.
【详解】解:连接,
在的内接四边形中,,
,
,
,
,
,
∵四边形为圆的内接四边形,
,
.
故答案为:126.
15.
【分析】本题考查了圆周角定理、含角的直角三角形的性质、勾股定理、垂径定理、扇形面积公式,连接,,作于,由圆周角定理可得,从而得出,由含角的直角三角形的性质可得,由垂径定理可得,由勾股定计算出,,最后根据进行计算即可,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】解:如图,连接,,作于,
,
,
,
,
,
,
,,
,
,
,,
,
故答案为:.
16.
【分析】本题主要考查了三角形的外接圆,圆周角定理,等腰三角形的性质,勾股定理,三角形的三边关系,解题的关键是证明出,分析出D在以为弦,的圆弧上运动;再根据A、D、M三点共线时,最小即可求解
【详解】解:,
点D在以为弦,的圆弧上运动,如图所示,设D点运动的圆弧圆心为M,取优弧上一点N,
连接,
则
是等腰三角形,
当A、D、M三点共线时,最小,
此时,
故答案为:.
17.
【分析】本题主要考查了解一元二次方程,构成三角形的条件,先利用因式分解法解方程求出方程的两个根,再根据构成三角形的条件确定出第三边的长,最后根据三角形周长计算公式求解即可.
【详解】解:解方程得:或,
∵,
∴第三边长为5时能构成三角形,第三边长为7时不能构成三角形,
∴该三角形的周长为.
18.平均一个人传染了8个人,经过三轮传染后共有729人患上了流感
【分析】本题考查了一元二次方程的应用,关键是根据题意列方程求解.设平均一人传染了x人,根据有一人患了流感,经过两轮传染后共有81人患了流感,列方程求出x的值,进而表示出经过三轮传染后患上流感的人数.
【详解】解:设平均一人传染了x人,
,
解得(不符合题意,舍去)
经过三轮传染后患上流感的人数为:(人),
答:平均一个人传染了8个人,经过三轮传染后共有729人患上了流感.
19.七、八月份该团购券销售量的月平均增长率为.
【分析】本题考查一元二次方程的实际应用.设七、八月份该团购券销售量的月平均增长率为.根据六月份销售量乘以等于八月份的销售量,列出方程求解即可.
【详解】解:设七、八月份该团购券销售量的月平均增长率为.
根据题意,得,
解得(不符合题意,舍去).
答:七、八月份该团购券销售量的月平均增长率为.
20.(1);
(2).
【分析】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
(1)直接根据概率公式求解即可;
(2)画树状图展示所有16种等可能的结果数,找出小明与小亮抽到同一卡片的结果数,然后根据概率公式计算.
【详解】(1)解:小明抽到A卡片的概率是;
(2)解:画树状图为:
共有16种等可能的结果数,其中小明与小丽抽到同一卡片的结果数为4,
所以小明与小丽抽到同一地点的概率.
21.(1)
(2)
【分析】本题考查了旋转的性质、坐标与图形、三角形全等的判定与性质、勾股定理、扇形面积的计算,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)根据旋转的性质作出即可,由旋转的性质可得,,作轴于,轴于,则,证明得到,,由,,得出,,,从而得出,,,即可得到答案;
(2)作轴于,轴于 ,由,,结合勾股定理可得,,由旋转的性质可得,,则,再根据,进行计算即可.
【详解】(1)解:如图,即为所作,
,
由旋转的性质可得,,
作轴于,轴于,则,
,,
,
,
,,
,,
,,,
,,
,
,
故答案为:;
(2)解:如图,作轴于,轴于 ,
,
,,,
,,,,
,
,,
由旋转的性质可得,,
,
由图可得:旋转过程中边扫过的面积为:
.
22.(1)见解析
(2)
【分析】(1)连接,则,所以,由,得,则,所以,则,即可证明是的切线;
(2)连接,由是的直径,得,由30度角的性质可求出,根据勾股定理求出,然后再由30度角的性质即可求解.
【详解】(1)如图,连接.
,.
.
.
.
,
.
是的半径,
是的切线.
(2)如图,连接.
是的直径,
.
,,
,.
在中,.
.
【点睛】此题考查等腰三角形的性质,平行线的判定与性质,切线的判定定理,圆周角定理,30度角所对的直角边等于斜边的一半,以及勾股定理等知识,正确作出辅助线是解题的关键.
23.(1)证明见解析
(2)证明见解析
(3)
【分析】本题考查了圆的综合题:熟练掌握圆周角定理和等边三角形的判定与性质;会运用三角形全等证明线段相等或角相等;会运用含的直角三角形三边的关系进行几何计算.(1)如图①,根据圆周角定理得到,然后根据等边三角形的判定方法即可证明;(2)如图①,由是等边三角形得,再利用“”证明,得到,,接着证明,即可证明;(3)如图②,由为直径,得,再利用,则;由于是等边三角形,则,然后在中根据含的直角三角形三边的关系可计算出的长.
【详解】(1)证明:如图①
,
而,
是等边三角形;
(2)证明:如图①
是等边三角形,
,
在和中,
,
(),
,
,
,
即,
是等边三角形;
(3)如图②,点和圆心重合,即为直径,
,
是等边三角形,
,
,
是等边三角形,
,
在中,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末经典题型检测卷-2023-2024学年数学九年级上册苏科版
一、单选题
1.下列方程一定是一元二次方程的是( )
A. B.
C. D.
2.若关于x的一元二次方程的一个根是,则m的值为( )
A. B.1 C. D.2
3.在一次体育测试中,嘉琪所在小组人的成绩分别是:,,,,..则这人体育测试成绩的中位数是( )
A.47 B.48 C. D.49
4.下列命题中,真命题的个数是( )
①圆的每一条直径都是它的对称轴;②平分弦的直径必定垂直于这条弦;③在同圆或等圆中,相等的圆心角所对的弧相等;④在同圆中,相等的弦所对的弧相等.
A.4个 B.3个 C.2个 D.1个
5.参加足球联赛的每两队之间都进行两场比赛,共要比赛场,设共有个队参加比赛,则下列方程符合题意的是( )
A. B.
C. D.
6.如图,是的直径,垂直于弦于点D,的延长线交于点E.若,,则的长是( )
A.1 B. C.2 D.4
7.如图,在中,弦的长,圆心到的距离是,那么的半径是( )
A. B. C. D.
8.如图,、、是上的三点,并且,点是圆上的一个动点点不与点、、重合,连接、,则的度数是( )
A. B. C.或 D.或
二、填空题
9.一元二次方程的根的情况是 .
10.若圆锥的底面圆半径为2,母线长为5,则该圆锥的侧面积是 .
11.圆周率是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对有过深入的研究.目前,超级计算机已计算出的小数部分超过31.4万亿位.有学者发现,这10个数字出现的频率趋于稳定接近相同,从的小数部分随机取出一个数字,估计数字是6的概率为 .
12.已知关于x的一元二次方程的两根为,则 .
13.在方差计算公式中,可以看出的值为 .
14.如图,在的内接四边形中,,点E在上,则 .
15.如图,在中,,是的外接圆,,则图中阴影部分的面积 (结果保留和根号).
16.如图,中,,,,D为内一动点,为的外接圆,交于点E,直线交于点P,,则的最小值为 .
三、解答题
17.一个三角形两边长是3和4,第三边的长是方程的根,求该三角形的周长.
18.随着人们生活水平的提高,节假日大家都喜欢游览观光祖国的大好河山,但一定要注意安全,特别要防止病毒的传染.我们利用学过的数学知识来解决一个关于病毒传染的问题:一个游客在旅游时,因不意防范,患上了流感,回家后,经两轮传染后有81人患上了流感,那么平均一个人传染了几个人?经过三轮传染后共有多少人患上了流感?
19.某餐饮店开拓线上团购业务,于今年五月底上线团购券,六月份销售了256张,七、八月份该团购券十分畅销,销售量持续走高,在售价不变的基础上,八月份的销售量达到400张,求七、八月份该团购券销售量的月平均增长率.
20.广州的白云山、越秀山、莲花山和大夫山被誉为广州四大名山,不仅风景秀美而且有丰厚的历史底蕴,是广州市民喜欢游玩之地.小明、小丽两家人决定周末去游玩,并用抽卡片的方式从白云山、越秀山、莲花山和大夫山(分别记为、、、)选出一个景点.他们准备了张不透明的卡片,正面分别写上、、和.卡片除正面字母不同外其余均相同.
(1)小明随机抽取一张卡片,则抽取到卡片的概率是_______;
(2)小明随机抽取一张卡片后,放回洗匀,小丽再随机抽取一张卡片,请用列或画树状图的方法求他们都抽取到同一地点的概率.
21.如图,在平面直角坐标系中,的三个顶点的坐标分别为,,.将绕点顺时针旋转,得到,
(1)画出,并直接写出点的坐标为 .
(2)求出旋转过程中边扫过的面积.
22.如图,在中,,以为直径的交于点,,垂足为.
(1)求证:是的切线;
(2)若,,求的长.
23.如图①,点、、在上,且,是弧上的一点,(点不与点、重合),连接、、,在上截取,连接.若,解答下列问题:
(1)求证:是等边三角形;
(2)求证:是等边三角形;
(3)如图②,若点和圆心重合,,则的长为 .
参考答案:
1.C
【分析】本题主要考查了一元二次方程的定义;只含有一个未知数,且未知数的最高次数是2的整式方程叫做一元二次方程.一元二次方程有三个特点:只含有一个未知数;未知数的最高次数是2;是整式方程.
【详解】解:A. 是二元一次方程,故本选项不符合题意;
B. 当时,不是一元二次方程,故本选项不符合题意;
C. 是一元二次方程,故本选项符合题意
D. 是分式方程,故本选项不符合题意;
故选:C.
2.B
【分析】根据一元二次方程的根的定义把方程根代入,得到关于m的方程,解方程即可得到m的值.此题考查了一元二次方程,熟练掌握一元二次方程根的定义是解题的关键.
【详解】解:∵关于x的一元二次方程的一个根是,
∴,
解得,
故选:B
3.B
【分析】本题考查了中位数的知识,解答本题的关键是掌握中位数的定义,注意在求解前观察:数据是否按大小顺序排列.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数,由此计算即可.
【详解】解:将这组数据从小到大排序后,这组数据的中间两个数为,,
这组数据的中位数为.
故选:B.
4.D
【分析】本题考查判断命题的真假,圆的对称性,垂径定理,圆周角定理.掌握相关知识点,是解题的关键.
【详解】解:①圆的每一条直径所在的直线都是它的对称轴;故①是假命题;
②平分弦(不是直径)的直径必定垂直于这条弦;故②是假命题;
③在同圆或等圆中,相等的圆心角所对的弧相等;故③是真命题;
④在同圆中,一弦对两弧,所以相等的弦所对的弧不一定相等,故④是假命题;
故选D.
5.D
【分析】本题考查了一元二次方程的应用,熟练掌握每两队之间都进行两场比赛的意义是解题的关键.
【详解】根据题意,得,
故选D.
6.C
【分析】本题主要考查了垂径定理,勾股定理,圆周角定理,由垂径定理得到,设,则,由勾股定理得,解方程求出,由是的直径,得到,,则.
【详解】解:∵,
∴,,
设,则,
在中,由勾股定理得,
∴,
解得,
∵是的直径,
∴,
∴,
故选C.
7.B
【分析】本题考查了勾股定理与垂径定理;根据图形可得,在中,勾股定理,即可求解.
【详解】解:∵弦的长,圆心到的距离是,
∴,
在中,,
故选:B.
8.D
【分析】本题考查了圆周角定理,圆内接四边形对角互补;根据同弧所对的圆周角相等以及圆内接四边形对角互补即可求解.
【详解】解:如图所示,
当在上时,,
当在上时,,
故选:D.
9.有两个不相等的实数根
【分析】此题考查了一元二次方程根的判别式.求根的判别式,进而得出答案.
【详解】解:∵,
∴一元二次方程有两个不相等的实数根
故答案为:有两个不相等的实数根.
10.
【分析】此题主要考查了圆锥侧面积公式,根据圆锥的底面半径为2,母线长为5,直接利用圆锥的侧面积公式求出它的侧面积即可.
【详解】解:根据圆锥侧面积公式:,
故答案为:.
11.
【分析】本题考查了利用频率估计概率,掌握大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率是解题的关键.
从的小数部分随机取出一个数字共有10种等可能的结果,其中出现数字6的只有1种结果,利用概率公式求解即可.
【详解】解:∵随着小数部分位数的增加,这10个数字出现的频率趋于稳定接近相同,
∴从的小数部分随机取出一个数字共有10种等可能的结果,其中出现数字2的只有1种结果,
∴P(数字是6).
故答案为:.
12.
【分析】本题主要考查了一元二次方程根与系数的关系,对于一元二次方程,若是该方程的两个实数根,则,据此求出,再代值计算即可.
【详解】解:∵关于x的一元二次方程的两根为,
∴,
∴,
故答案为:.
13.
【分析】本题考查了方差与平均数的计算,由方差的计算可得这组数据的平均数,然后利用平均数的计算方法即可求解,掌握方差的计算公式是解题的关键.
【详解】解:由题意可得,这组数据共个数,且它们的平均数是,
∴,
故答案为:.
14.126
【分析】本题考查了圆内接四边形的性质:圆内接四边形的对角互补.等腰三角形的性质和三角形内角和定理.先根据圆内接四边形的性质计算出,再根据等腰三角形的性质和三角形内角和定理计算出,然后再根据圆内接四边形的性质可得的度数.
【详解】解:连接,
在的内接四边形中,,
,
,
,
,
,
∵四边形为圆的内接四边形,
,
.
故答案为:126.
15.
【分析】本题考查了圆周角定理、含角的直角三角形的性质、勾股定理、垂径定理、扇形面积公式,连接,,作于,由圆周角定理可得,从而得出,由含角的直角三角形的性质可得,由垂径定理可得,由勾股定计算出,,最后根据进行计算即可,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】解:如图,连接,,作于,
,
,
,
,
,
,
,,
,
,
,,
,
故答案为:.
16.
【分析】本题主要考查了三角形的外接圆,圆周角定理,等腰三角形的性质,勾股定理,三角形的三边关系,解题的关键是证明出,分析出D在以为弦,的圆弧上运动;再根据A、D、M三点共线时,最小即可求解
【详解】解:,
点D在以为弦,的圆弧上运动,如图所示,设D点运动的圆弧圆心为M,取优弧上一点N,
连接,
则
是等腰三角形,
当A、D、M三点共线时,最小,
此时,
故答案为:.
17.
【分析】本题主要考查了解一元二次方程,构成三角形的条件,先利用因式分解法解方程求出方程的两个根,再根据构成三角形的条件确定出第三边的长,最后根据三角形周长计算公式求解即可.
【详解】解:解方程得:或,
∵,
∴第三边长为5时能构成三角形,第三边长为7时不能构成三角形,
∴该三角形的周长为.
18.平均一个人传染了8个人,经过三轮传染后共有729人患上了流感
【分析】本题考查了一元二次方程的应用,关键是根据题意列方程求解.设平均一人传染了x人,根据有一人患了流感,经过两轮传染后共有81人患了流感,列方程求出x的值,进而表示出经过三轮传染后患上流感的人数.
【详解】解:设平均一人传染了x人,
,
解得(不符合题意,舍去)
经过三轮传染后患上流感的人数为:(人),
答:平均一个人传染了8个人,经过三轮传染后共有729人患上了流感.
19.七、八月份该团购券销售量的月平均增长率为.
【分析】本题考查一元二次方程的实际应用.设七、八月份该团购券销售量的月平均增长率为.根据六月份销售量乘以等于八月份的销售量,列出方程求解即可.
【详解】解:设七、八月份该团购券销售量的月平均增长率为.
根据题意,得,
解得(不符合题意,舍去).
答:七、八月份该团购券销售量的月平均增长率为.
20.(1);
(2).
【分析】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
(1)直接根据概率公式求解即可;
(2)画树状图展示所有16种等可能的结果数,找出小明与小亮抽到同一卡片的结果数,然后根据概率公式计算.
【详解】(1)解:小明抽到A卡片的概率是;
(2)解:画树状图为:
共有16种等可能的结果数,其中小明与小丽抽到同一卡片的结果数为4,
所以小明与小丽抽到同一地点的概率.
21.(1)
(2)
【分析】本题考查了旋转的性质、坐标与图形、三角形全等的判定与性质、勾股定理、扇形面积的计算,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)根据旋转的性质作出即可,由旋转的性质可得,,作轴于,轴于,则,证明得到,,由,,得出,,,从而得出,,,即可得到答案;
(2)作轴于,轴于 ,由,,结合勾股定理可得,,由旋转的性质可得,,则,再根据,进行计算即可.
【详解】(1)解:如图,即为所作,
,
由旋转的性质可得,,
作轴于,轴于,则,
,,
,
,
,,
,,
,,,
,,
,
,
故答案为:;
(2)解:如图,作轴于,轴于 ,
,
,,,
,,,,
,
,,
由旋转的性质可得,,
,
由图可得:旋转过程中边扫过的面积为:
.
22.(1)见解析
(2)
【分析】(1)连接,则,所以,由,得,则,所以,则,即可证明是的切线;
(2)连接,由是的直径,得,由30度角的性质可求出,根据勾股定理求出,然后再由30度角的性质即可求解.
【详解】(1)如图,连接.
,.
.
.
.
,
.
是的半径,
是的切线.
(2)如图,连接.
是的直径,
.
,,
,.
在中,.
.
【点睛】此题考查等腰三角形的性质,平行线的判定与性质,切线的判定定理,圆周角定理,30度角所对的直角边等于斜边的一半,以及勾股定理等知识,正确作出辅助线是解题的关键.
23.(1)证明见解析
(2)证明见解析
(3)
【分析】本题考查了圆的综合题:熟练掌握圆周角定理和等边三角形的判定与性质;会运用三角形全等证明线段相等或角相等;会运用含的直角三角形三边的关系进行几何计算.(1)如图①,根据圆周角定理得到,然后根据等边三角形的判定方法即可证明;(2)如图①,由是等边三角形得,再利用“”证明,得到,,接着证明,即可证明;(3)如图②,由为直径,得,再利用,则;由于是等边三角形,则,然后在中根据含的直角三角形三边的关系可计算出的长.
【详解】(1)证明:如图①
,
而,
是等边三角形;
(2)证明:如图①
是等边三角形,
,
在和中,
,
(),
,
,
,
即,
是等边三角形;
(3)如图②,点和圆心重合,即为直径,
,
是等边三角形,
,
,
是等边三角形,
,
在中,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
