期末经典题型练习卷2023-2024学年数学九年级上册苏科版(含解析)
文档属性
| 名称 | 期末经典题型练习卷2023-2024学年数学九年级上册苏科版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 14:24:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末经典题型练习卷2023-2024学年数学九年级上册苏科版
一、单选题
1.现有4根木棒,长度分别为、、、,从中任取三根木棒,能够组成三角形的概率是( )
A. B. C. D.
2.某超市招聘收银员一名,对四名申请人进行了三项素质测试.四名候选人的素质测试成绩如下表.公司根据实际需要,对计算机、语言、商品知识三项测试成绩分别赋予权4,3,2后录用最高分,这四人中将被录用的是( )
素质测试 测试成绩
小赵 小钱 小孙 小李
计算机
语言
商品知识
A.小赵 B.小钱 C.小孙 D.小李
3.如图中的数轴可以度量图中圆的直径,则此直径是()
A. B. C. D.
4.已知是方程的一个根,则另一个根的值是( )
A. B.1 C. D.2
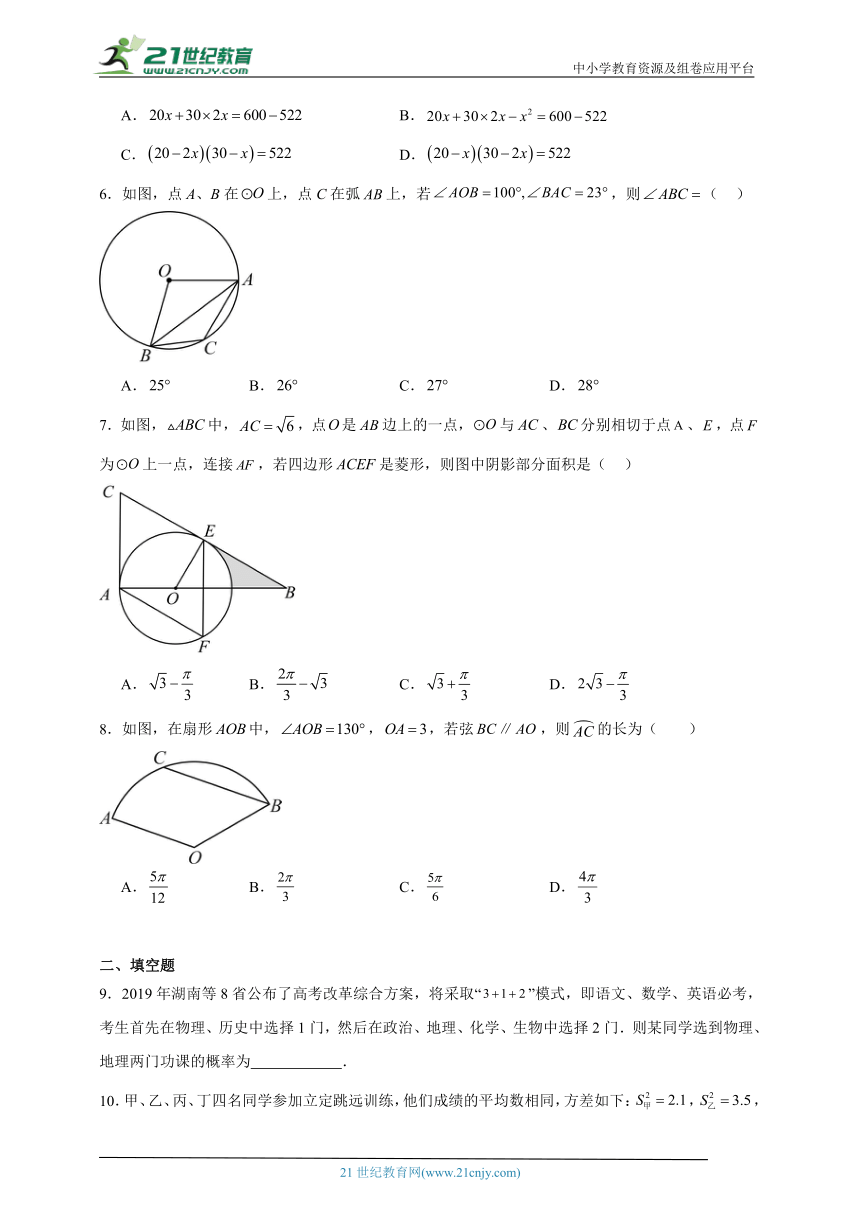
5.如图,在一块长,宽的矩形苗圃基地上修建两横一纵三条等宽的道路,剩余空地种植花苗,设道路的宽为,若种植花苗的面积为,依题意列方程为( )
A. B.
C. D.
6.如图,点A、B在上,点C在弧上,若,则( )
A. B. C. D.
7.如图,中,,点是边上的一点,与、分别相切于点、,点为上一点,连接,若四边形是菱形,则图中阴影部分面积是( )
A. B. C. D.
8.如图,在扇形中,,,若弦,则的长为( )
A. B. C. D.
二、填空题
9.2019年湖南等8省公布了高考改革综合方案,将采取“”模式,即语文、数学、英语必考,考生首先在物理、历史中选择1门,然后在政治、地理、化学、生物中选择2门.则某同学选到物理、地理两门功课的概率为 .
10.甲、乙、丙、丁四名同学参加立定跳远训练,他们成绩的平均数相同,方差如下:,,,,则成绩最稳定的同学是 .(填写甲或乙或丙或丁)
11.为了弘扬传统文化,某校举行了“书香校园,师生共读”演讲比赛,下表是小红在演讲比赛中的得分情况(单位:分),评分时,对服装、普通话、主题、演讲技巧四项赋权,则小红的综合得分是 .
选手 服装 普通话 主题 演讲技巧
小红 85 70 80 85
12.已知,是一元二次方程的两个实数根,则的值为 .
13.如果关于x的一元二次方程有两个实数根,且其中一个根为另外一个根的2倍,则称这样的方程为“倍根方程”,若关于x的方程是倍根方程.则p,q需满足 .
14.对于一元二次方程,下列说法:
①若方程有一根,则;
②若,则;
③若方程的两个根是,那么方程的两个根为;
④若c是方程的一个根,则一定有成立.
其中正确的是 .(填序号)
15.如图,在中,弧弧,,点在上,连接,则 .
16.如图,是的切线,切点为A,,,则的半径长为
17.如图,四边形内接于,、的延长线相交于点E,、的延长线相交于点F.若,,则的度数为 .
18.如图,点A是半圆上的一个三等分点,点是的中点,是直径上一动点,的半径是2,则的最小值为 .
三、解答题
19.按要求解方程
(1)用配方法解方程;
(2)用公式法解方程;
(3)用因式分解法解方程.
20.在一个不透明的口袋里分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全样,正面分别写有数字6、7、8的卡片,现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
(2)小红和小莉做游戏,制定了两个游戏规则,规则1:若两次摸出的数字,至少有一次是“6”,小红赢,否则,小莉赢;规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢,否则,小莉赢.小红想要在游戏中获胜,她会选择哪一条规则,并说明理由.
21.为弘扬向善、为善优秀品质,助力爱心公益事业,我校组织“人间自有真情在,爱心助力暖人心”慈善捐款活动,八年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况,统计结果如图①和图②所示.
(1)本次共抽查了________人;并补全上面条形统计图;
(2)本次抽查学生捐款的中位数为________;众数为________;
(3)全校有八年级学生1100人,估计捐款金额超过15元(不含15元)的有多少人?
22.已知关于的一元二次方程
(1)求证:无论取何值,方程都有两个不相等的实数解;
(2)设方程的两个实数解分别为,且满足,求实数的值.
23.年亚运会在杭州顺利召开,亚运会吉祥物莲莲爆红。
(1)据统计某莲莲玩偶在某电商平台月份的销售量是万件,月份的销售量是万件,问月平均增长率是多少?
(2)市场调查发现,某实体店莲莲玩偶的进价为每件元,若售价为每件元,每天能销售件,售价每降价元,每天可多售出件,为了推广宣传,商家决定降价促销,同时尽量减少库存,若使销售莲莲玩偶每天获利元,则售价应降低多少元?
24.如图,已知是的直径,点是上一点,连接,点为的中点,连接交于点.
(1)求证:.
(2)若,,求BC长.
25.已知,在半圆中,直径,点、在半圆上运动,(点、可以与A、两点重合),弦.
(1)如图1,当时,求证;
(2)如图2,若时,求图中阴影部分(弦、直径、弧围成的图形)的面积;
(3)如图3,取的中点M,点C从点A开始运动到点D与点B重合时结束,在整个运动过程中:
①点M到的距离的最大值是______;
②直接写出点M的运动路径长______.
26.如图,在,,的平分线交于点,过点作直线的垂线交于点,是的外接圆.
(1)求证:是的切线;
(2)过点作于点,求证:平分;
(3)求证:.
参考答案:
1.C
【分析】本题主要考查了概率公式,解决问题的关键是根据三角形三边之间的关系与概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
【详解】解:有四根木棒,长度分别为、、、,
从中任取三根木棒,共有4种等可能出现的结果:、、;、、;、、;、、;
根据三角形两边之和大于第三边可知,、、不能组成三角形,
则能组成三角形的有3种,
∴能够组成三角形的概率为.
故选:C.
2.B
【分析】本题考查加权平均数,利用各项乘以各项权数,除以总权数即可得到答案;
【详解】解:由题意可得,
小赵:,
小钱:,
小孙:,
小李:,
∵,
∴小钱被录用,
故选:B.
3.B
【分析】本题考查了圆的切线及数轴的定义,根据“数轴上两点的距离等于右边的数减去左边的数”即可得到答案.
【详解】解:图中圆的直径为,
故选:B.
4.D
【分析】此题考查了一元二次方程的根与系数的关系,为一元二次方程的两根,则,,根据两个乘积已知,再除以已知的根即可得到另一个根,据此解答
【详解】解:∵方程两个根的乘以等于 ,
∴另一个根是
故选:D
5.C
【分析】本题考查了由实际问题抽象出一元二次方程,设道路的宽为,则种植花苗的部分可合成长,宽的矩形,根据种植花苗的面积为,即可得出关于x的一元二次方程,此题得解.
【详解】解:设道路的宽为,则种植花苗的部分可合成长,宽的矩形,
依题意得:,
故选:C.
6.C
【分析】题目主要考查圆周角定理及圆内接四边求角度,三角形内角和定理,根据题意得出弧所对的圆周角的度数为:,然后确定,再由三角形内角和定理即可求解,熟练掌握圆周角定理及内接四边形的性质是解题关键.
【详解】解:∵,
∴弧所对的圆周角的度数为:,
∴,
∵,
,
故选:C.
7.A
【分析】本题考查的是切线的性质,菱形的性质、扇形面积计算、圆周角定理,掌握圆的切线垂直于经过切点的半径、弧长公式是解题的关键.根据菱形的性质得到,根据圆周角定理得到,根据切线的性质得到,求出,根据直角三角形的性质、扇形面积公式计算,得到答案.
【详解】解:∵四边形是菱形,
∴,
由圆周角定理得:,
∵与、分别相切于点、,
∴,
∴,
,
,
,,
,
,,
,
,
故选:A.
8.C
【分析】本题考查平行线的性质,等腰三角形的性质,熟练掌握平行线的性质与等边对等角的等腰三角形的性质是解题的关键.
先根据平行线的性质求得,,再由等腰三角形的性质,即可求解.
【详解】解:连接,如图,
∵,
∴,,
∵,
∴,
∵,
∴,
∴,
∴的长.
故选:C.
9.
【分析】本题考查画树状图或列表法求概率.画出树状图分析出所有可能的结果数和选到物理、地理两门功课数,然后用概率公式计算即可.
【详解】解:物理、历史、政治、地理、化学、生物分别用字母A、B、C、D、E、F表示,
画树状图如图,
所有可能的选择结果共有24种,选择A、D(即物理、地理)两门功课的有6种,
所以某同学选到物理、地理两门功课的概率为.
故答案为:.
10.丁
【分析】本题考查根据方差判断稳定性,方差越小,成绩越稳定,由此可解.
【详解】解:甲、乙、丙、丁成绩的平均数相同,,
成绩最稳定的同学是丁,
故答案为:丁.
11.80
【分析】此题考查加权平均数,已知各项的权重,利用加权平均法可以求出小红得综合成绩.
【详解】小红的综合成绩为:(分);
故答案为:80.
12.5
【分析】根据一元二次方程根与系数的关系直接进行求解即可.本题考查一元二次方程根与系数的关系和完全平方公式,熟练掌握根与系数的关系是解题的关键.
【详解】解:∵a,b是一元二次方程的两个实数根,
∴
.
故答案为:5.
13.2
【分析】本题考查了一元二次方程的根与系数的关系,熟练掌握一元二次方程的根与系数的关系是解题关键.设关于的一元二次方程的两个根分别为,再利用一元二次方程的根与系数的关系求解即可得.
【详解】解:由题意,设关于的一元二次方程的两个根分别为,
则,且,
由①得:,
将代入②得:,
则,
故答案为:2.
14.①②③
【分析】本题考查一元二次方程的解,根的判别式,分别根据一元二次方程的解,根的判别式判断即可.
【详解】解:①若方程有一根,则,故正确;
②若,则可知方程有一个根为,
则,故正确;
③若方程的两个根是,
则或4,
所以方程的两个根为,故正确;
④若c是方程的一个根,
则,
当时,则一定有成立,故错误.
所以其中正确的是①②③.
故答案为:①②③.
15./20度
【分析】本题考查了同圆中等弧所对的圆心角相等,圆周角定理.熟练掌握圆周角定理是解题的关键.
如图,连接,则,根据圆周角定理求解即可.
【详解】解:如图,连接,
∵,
∴,
∵,
∴,
故答案为:.
16.2
【分析】本题考查切线性质、含30度角的直角三角形的性质,关键是掌握切线性质.先利用切线性质得到,再利用直角三角形中,30度角所对的直角边等于斜边的一半求解即可.
【详解】解:∵是的切线,切点为A,
∴,即,
∵,,
∴,
故答案为:2.
17./46度
【分析】本题考查了圆内接四边形的性质,三角形的外角性质.先两次根据三角形的外角定理,得,再根据圆内接四边形的性质,得,即可得出结果.
【详解】解:∵ 是的外角,
∴,
∵是的外角,
∴,
∴,
∵四边形内接于,
∴,
∴,
∴.
故答案为:.
18.
【分析】本题主要考查了圆心角的性质,轴对称的性质,勾股定理,解题的关键是作点A关于的对称点,连接交于P,则点P即是所求作的点,根据勾股定理求出结果即可.
【详解】解:如图,作点A关于的对称点,连接交于P,则点P即是所求作的点,
根据轴对称的性质可知,,
∴,
∵两点之间线段最短,
∴ 此时最小,即最小,
∴的最小值为的长,
∵A是半圆上一个三等分点,
∴,
又∵点B是的中点,
∴,
∴,
在中,由勾股定理得:
,
∴的最小值是.
故答案为:.
19.(1)
(2),
(3),
【分析】本题主要考查解一元二次方程,熟练掌握解一元二次方程的方法是解题的关键.
(1)利用配方法解方程即可;
(2)利用公式法解方程即可;
(3)利用因式分解法解方程即可.
【详解】(1)解:
;
(2)解:
,;
(3)解:
,.
20.(1)画树状图见解析,共有9种可能,分别是,,,,,,,,
(2)小红要想在游戏中获胜,她应该选择规则1
【分析】本题考查了列表法与树状图法,利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式计算事件或事件的概率,是解决问题的关键.
(1)利用列表法或者画出树状图,然后写出所有的可能情况即可.
(2)分别求出“至少有一次是“6””和“卡片上的数字是球上数字的整数倍”的概率,小红选择自己获胜的概率比小莉获胜的概率大的一种规则即可在游戏中获胜.
【详解】(1)解:画树状图如下:
∴共有9种可能,分别是,,,,,,,,.
(2)规则1:由(1)可知,至少有一次是“6”的情况有5种,
∴小红赢的概率是(至少有一次是“6”),小莉赢的概率是.
∵,
∴此规则小红获胜的概率大.
规则2:卡片上的数字是球上数字的整数倍的有:,,,共4种情况,
∴小红赢的概率是(卡片上的数字是球上数字的整数倍),小莉赢的概率是.
∵,
∴此规则小莉获胜的概率大.
∴小红要想在游戏中获胜,她应该选择规则1.
21.(1)50,补图见解析
(2)15,15
(3)220人
【分析】本题考查扇形统计图,条形统计图,中位数、众数以及样本估计总体,
(1)从两个统计图中可知,样本中“捐款为5元”的学生有8人,占调查人数的,根据频率可求出答案;
(2)根据众数、中位数的定义进行计算即可;
(3)求出样本捐款金额超过15元(不含15元)的所占百分比,估计总体中捐款金额超过15元(不含15元)人数.
【详解】(1)解: (人,
“捐款为15元”的学生有(人,补全条形统计图如下:
(2)学生捐款金额出现次数最多的是15元,共出现18次,因此捐款金额的众数是15元,
将这50名学生捐款金额从小到大排列处在中间位置的两个数都是15元,因此中位数是15元,
故答案为:15,15;
(3)捐款金额超过15元(不含15元)的人数(人),
所以全校八年级学生为1100名,捐款金额超过15元(不含15元)的人数为220人,
22.(1)见解析
(2)或
【分析】本题主要考查一元二次方程的判别式以及根与系数的关系,熟练掌握根与系数的关系是解题的关键.
(1)根据根的判别式证明即可;
(2)由根与系数的关系求出的值即可得到答案.
【详解】(1)证明:由题意化简得
无论取和值,总有,
故无论取何值,方程都有两个不相等的实数解;
(2)解:由根与系数的关系,得,
,
,
,
,
解得.
23.(1)
(2)
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)设月平均增长率是,利用月份的销售量月份的销售量(月平均增长率),即可得出关于的一元二次方程,解之取其正值即可;
(2)设售价应降低元,则每件的销售利润为元,每天的销售量为件,利用每天的利润每件的销售利润日销售量,即可得出关于的一元二次方程,再结合要尽量减少库存,即可求解.
【详解】(1)设月平均增长率是,
根据题意得:,
解得:,(不符合题意,舍去),
月平均增长率是;
(2)设售价应降低元,则每件的销售利润为元,每天的销售量为件,
依据题意得:,
即,
解得:,,
要尽量减少库存,
,
售价应降低元.
24.(1)证明见解析
(2)
【分析】本题考查了圆周角定理,垂径定理,勾股定理,圆心角、弧、弦的关系,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)由圆周角定理可得,由点为的中点得出,从而得到,即可得证;
(2)由垂径定理可得,设半径为,在中,由勾股定理得,,求出半径,得出,最后由勾股定理进行计算即可.
【详解】(1)证明:是的直径,
∴,
∵点为的中点,
∴,
∴,
∴;
(2)解:∵,,
∴,
设半径为,在中,由勾股定理得,,
解得:,
∴,
∵,
∴.
25.(1)见解析
(2)图中阴影部分的面积为;
(3)①;②
【分析】(1)由可得,从而由可证明;
(2)过D作于H,由,可得,即知,,故,即得;
(3)①连接,过M作于E,根据直径,弦,可得是等边三角形,而M是的中点,即知,即得当最大时,最小,而是等边三角形,即可得点M到的距离的最小值是;
②根据,知M的轨迹是以O为圆心,为半径的弧,当C与A重合时,,即可得,故点M的运动路径长为.
【详解】(1)证明:∵,
∴,
∵,
∴,即,
在和中,
,
∴;
(2)解:过D作于H,如图:
∵半圆O中,直径,
∴,
∵,
∴,
∴,
∴,,
∴;
答:阴影部分面积是;
(3)解:①连接,过M作于E,如图:
∵直径,弦,
∴,
∴是等边三角形,
∵M是的中点,
∴,
∴,
∴,
∴当最大时,最小,
而当C与A重合(或D与B重合)时,最大,如图:
∵是等边三角形,M是的中点,
∴,
∴,
即点M到的距离的最小值是,
故答案为:;
②如图,
由①知:,M的轨迹是以O为圆心,为半径的弧,
当C与A重合时,,
同理,当D与B重合时,,
∴,
∴点M的运动路径长为,
故答案为:.
【点睛】本题考查圆的综合应用,涉及全等三角形的判定,圆的性质及圆中的相关计算,解题的关键是掌握M点的轨迹是以O为圆心,为半径的弧.
26.(1)见解析
(2)见解析
(3)见解析
【分析】本题主要考查了角平分线的定义,平行线的性质与判定,圆切线的判定,直径所对的圆周角是直角,等腰三角形的性质等等,解题的关键在于能够熟练掌握相关知识进行求解.
(1)如图,连接,由,得到,则是圆O的直径,可以推出,由平分,得到,则 ,可证,由此即可证明;
(2)由,,推出,再由,,即可得到,则平分.
(3)连结DE,先根据AAS证明,再由全等三角形的对应边相等即可得出.
【详解】(1)解:如图,连接.
,
是圆的直径,
,
平分,
,
,
,
是的切线.
(2)解:∵,
∴,
∵,
∴,
∴,
∴平分.
(3)解:如图,连结.
是的平分线,于,于,
.
,,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末经典题型练习卷2023-2024学年数学九年级上册苏科版
一、单选题
1.现有4根木棒,长度分别为、、、,从中任取三根木棒,能够组成三角形的概率是( )
A. B. C. D.
2.某超市招聘收银员一名,对四名申请人进行了三项素质测试.四名候选人的素质测试成绩如下表.公司根据实际需要,对计算机、语言、商品知识三项测试成绩分别赋予权4,3,2后录用最高分,这四人中将被录用的是( )
素质测试 测试成绩
小赵 小钱 小孙 小李
计算机
语言
商品知识
A.小赵 B.小钱 C.小孙 D.小李
3.如图中的数轴可以度量图中圆的直径,则此直径是()
A. B. C. D.
4.已知是方程的一个根,则另一个根的值是( )
A. B.1 C. D.2
5.如图,在一块长,宽的矩形苗圃基地上修建两横一纵三条等宽的道路,剩余空地种植花苗,设道路的宽为,若种植花苗的面积为,依题意列方程为( )
A. B.
C. D.
6.如图,点A、B在上,点C在弧上,若,则( )
A. B. C. D.
7.如图,中,,点是边上的一点,与、分别相切于点、,点为上一点,连接,若四边形是菱形,则图中阴影部分面积是( )
A. B. C. D.
8.如图,在扇形中,,,若弦,则的长为( )
A. B. C. D.
二、填空题
9.2019年湖南等8省公布了高考改革综合方案,将采取“”模式,即语文、数学、英语必考,考生首先在物理、历史中选择1门,然后在政治、地理、化学、生物中选择2门.则某同学选到物理、地理两门功课的概率为 .
10.甲、乙、丙、丁四名同学参加立定跳远训练,他们成绩的平均数相同,方差如下:,,,,则成绩最稳定的同学是 .(填写甲或乙或丙或丁)
11.为了弘扬传统文化,某校举行了“书香校园,师生共读”演讲比赛,下表是小红在演讲比赛中的得分情况(单位:分),评分时,对服装、普通话、主题、演讲技巧四项赋权,则小红的综合得分是 .
选手 服装 普通话 主题 演讲技巧
小红 85 70 80 85
12.已知,是一元二次方程的两个实数根,则的值为 .
13.如果关于x的一元二次方程有两个实数根,且其中一个根为另外一个根的2倍,则称这样的方程为“倍根方程”,若关于x的方程是倍根方程.则p,q需满足 .
14.对于一元二次方程,下列说法:
①若方程有一根,则;
②若,则;
③若方程的两个根是,那么方程的两个根为;
④若c是方程的一个根,则一定有成立.
其中正确的是 .(填序号)
15.如图,在中,弧弧,,点在上,连接,则 .
16.如图,是的切线,切点为A,,,则的半径长为
17.如图,四边形内接于,、的延长线相交于点E,、的延长线相交于点F.若,,则的度数为 .
18.如图,点A是半圆上的一个三等分点,点是的中点,是直径上一动点,的半径是2,则的最小值为 .
三、解答题
19.按要求解方程
(1)用配方法解方程;
(2)用公式法解方程;
(3)用因式分解法解方程.
20.在一个不透明的口袋里分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全样,正面分别写有数字6、7、8的卡片,现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
(2)小红和小莉做游戏,制定了两个游戏规则,规则1:若两次摸出的数字,至少有一次是“6”,小红赢,否则,小莉赢;规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢,否则,小莉赢.小红想要在游戏中获胜,她会选择哪一条规则,并说明理由.
21.为弘扬向善、为善优秀品质,助力爱心公益事业,我校组织“人间自有真情在,爱心助力暖人心”慈善捐款活动,八年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况,统计结果如图①和图②所示.
(1)本次共抽查了________人;并补全上面条形统计图;
(2)本次抽查学生捐款的中位数为________;众数为________;
(3)全校有八年级学生1100人,估计捐款金额超过15元(不含15元)的有多少人?
22.已知关于的一元二次方程
(1)求证:无论取何值,方程都有两个不相等的实数解;
(2)设方程的两个实数解分别为,且满足,求实数的值.
23.年亚运会在杭州顺利召开,亚运会吉祥物莲莲爆红。
(1)据统计某莲莲玩偶在某电商平台月份的销售量是万件,月份的销售量是万件,问月平均增长率是多少?
(2)市场调查发现,某实体店莲莲玩偶的进价为每件元,若售价为每件元,每天能销售件,售价每降价元,每天可多售出件,为了推广宣传,商家决定降价促销,同时尽量减少库存,若使销售莲莲玩偶每天获利元,则售价应降低多少元?
24.如图,已知是的直径,点是上一点,连接,点为的中点,连接交于点.
(1)求证:.
(2)若,,求BC长.
25.已知,在半圆中,直径,点、在半圆上运动,(点、可以与A、两点重合),弦.
(1)如图1,当时,求证;
(2)如图2,若时,求图中阴影部分(弦、直径、弧围成的图形)的面积;
(3)如图3,取的中点M,点C从点A开始运动到点D与点B重合时结束,在整个运动过程中:
①点M到的距离的最大值是______;
②直接写出点M的运动路径长______.
26.如图,在,,的平分线交于点,过点作直线的垂线交于点,是的外接圆.
(1)求证:是的切线;
(2)过点作于点,求证:平分;
(3)求证:.
参考答案:
1.C
【分析】本题主要考查了概率公式,解决问题的关键是根据三角形三边之间的关系与概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
【详解】解:有四根木棒,长度分别为、、、,
从中任取三根木棒,共有4种等可能出现的结果:、、;、、;、、;、、;
根据三角形两边之和大于第三边可知,、、不能组成三角形,
则能组成三角形的有3种,
∴能够组成三角形的概率为.
故选:C.
2.B
【分析】本题考查加权平均数,利用各项乘以各项权数,除以总权数即可得到答案;
【详解】解:由题意可得,
小赵:,
小钱:,
小孙:,
小李:,
∵,
∴小钱被录用,
故选:B.
3.B
【分析】本题考查了圆的切线及数轴的定义,根据“数轴上两点的距离等于右边的数减去左边的数”即可得到答案.
【详解】解:图中圆的直径为,
故选:B.
4.D
【分析】此题考查了一元二次方程的根与系数的关系,为一元二次方程的两根,则,,根据两个乘积已知,再除以已知的根即可得到另一个根,据此解答
【详解】解:∵方程两个根的乘以等于 ,
∴另一个根是
故选:D
5.C
【分析】本题考查了由实际问题抽象出一元二次方程,设道路的宽为,则种植花苗的部分可合成长,宽的矩形,根据种植花苗的面积为,即可得出关于x的一元二次方程,此题得解.
【详解】解:设道路的宽为,则种植花苗的部分可合成长,宽的矩形,
依题意得:,
故选:C.
6.C
【分析】题目主要考查圆周角定理及圆内接四边求角度,三角形内角和定理,根据题意得出弧所对的圆周角的度数为:,然后确定,再由三角形内角和定理即可求解,熟练掌握圆周角定理及内接四边形的性质是解题关键.
【详解】解:∵,
∴弧所对的圆周角的度数为:,
∴,
∵,
,
故选:C.
7.A
【分析】本题考查的是切线的性质,菱形的性质、扇形面积计算、圆周角定理,掌握圆的切线垂直于经过切点的半径、弧长公式是解题的关键.根据菱形的性质得到,根据圆周角定理得到,根据切线的性质得到,求出,根据直角三角形的性质、扇形面积公式计算,得到答案.
【详解】解:∵四边形是菱形,
∴,
由圆周角定理得:,
∵与、分别相切于点、,
∴,
∴,
,
,
,,
,
,,
,
,
故选:A.
8.C
【分析】本题考查平行线的性质,等腰三角形的性质,熟练掌握平行线的性质与等边对等角的等腰三角形的性质是解题的关键.
先根据平行线的性质求得,,再由等腰三角形的性质,即可求解.
【详解】解:连接,如图,
∵,
∴,,
∵,
∴,
∵,
∴,
∴,
∴的长.
故选:C.
9.
【分析】本题考查画树状图或列表法求概率.画出树状图分析出所有可能的结果数和选到物理、地理两门功课数,然后用概率公式计算即可.
【详解】解:物理、历史、政治、地理、化学、生物分别用字母A、B、C、D、E、F表示,
画树状图如图,
所有可能的选择结果共有24种,选择A、D(即物理、地理)两门功课的有6种,
所以某同学选到物理、地理两门功课的概率为.
故答案为:.
10.丁
【分析】本题考查根据方差判断稳定性,方差越小,成绩越稳定,由此可解.
【详解】解:甲、乙、丙、丁成绩的平均数相同,,
成绩最稳定的同学是丁,
故答案为:丁.
11.80
【分析】此题考查加权平均数,已知各项的权重,利用加权平均法可以求出小红得综合成绩.
【详解】小红的综合成绩为:(分);
故答案为:80.
12.5
【分析】根据一元二次方程根与系数的关系直接进行求解即可.本题考查一元二次方程根与系数的关系和完全平方公式,熟练掌握根与系数的关系是解题的关键.
【详解】解:∵a,b是一元二次方程的两个实数根,
∴
.
故答案为:5.
13.2
【分析】本题考查了一元二次方程的根与系数的关系,熟练掌握一元二次方程的根与系数的关系是解题关键.设关于的一元二次方程的两个根分别为,再利用一元二次方程的根与系数的关系求解即可得.
【详解】解:由题意,设关于的一元二次方程的两个根分别为,
则,且,
由①得:,
将代入②得:,
则,
故答案为:2.
14.①②③
【分析】本题考查一元二次方程的解,根的判别式,分别根据一元二次方程的解,根的判别式判断即可.
【详解】解:①若方程有一根,则,故正确;
②若,则可知方程有一个根为,
则,故正确;
③若方程的两个根是,
则或4,
所以方程的两个根为,故正确;
④若c是方程的一个根,
则,
当时,则一定有成立,故错误.
所以其中正确的是①②③.
故答案为:①②③.
15./20度
【分析】本题考查了同圆中等弧所对的圆心角相等,圆周角定理.熟练掌握圆周角定理是解题的关键.
如图,连接,则,根据圆周角定理求解即可.
【详解】解:如图,连接,
∵,
∴,
∵,
∴,
故答案为:.
16.2
【分析】本题考查切线性质、含30度角的直角三角形的性质,关键是掌握切线性质.先利用切线性质得到,再利用直角三角形中,30度角所对的直角边等于斜边的一半求解即可.
【详解】解:∵是的切线,切点为A,
∴,即,
∵,,
∴,
故答案为:2.
17./46度
【分析】本题考查了圆内接四边形的性质,三角形的外角性质.先两次根据三角形的外角定理,得,再根据圆内接四边形的性质,得,即可得出结果.
【详解】解:∵ 是的外角,
∴,
∵是的外角,
∴,
∴,
∵四边形内接于,
∴,
∴,
∴.
故答案为:.
18.
【分析】本题主要考查了圆心角的性质,轴对称的性质,勾股定理,解题的关键是作点A关于的对称点,连接交于P,则点P即是所求作的点,根据勾股定理求出结果即可.
【详解】解:如图,作点A关于的对称点,连接交于P,则点P即是所求作的点,
根据轴对称的性质可知,,
∴,
∵两点之间线段最短,
∴ 此时最小,即最小,
∴的最小值为的长,
∵A是半圆上一个三等分点,
∴,
又∵点B是的中点,
∴,
∴,
在中,由勾股定理得:
,
∴的最小值是.
故答案为:.
19.(1)
(2),
(3),
【分析】本题主要考查解一元二次方程,熟练掌握解一元二次方程的方法是解题的关键.
(1)利用配方法解方程即可;
(2)利用公式法解方程即可;
(3)利用因式分解法解方程即可.
【详解】(1)解:
;
(2)解:
,;
(3)解:
,.
20.(1)画树状图见解析,共有9种可能,分别是,,,,,,,,
(2)小红要想在游戏中获胜,她应该选择规则1
【分析】本题考查了列表法与树状图法,利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式计算事件或事件的概率,是解决问题的关键.
(1)利用列表法或者画出树状图,然后写出所有的可能情况即可.
(2)分别求出“至少有一次是“6””和“卡片上的数字是球上数字的整数倍”的概率,小红选择自己获胜的概率比小莉获胜的概率大的一种规则即可在游戏中获胜.
【详解】(1)解:画树状图如下:
∴共有9种可能,分别是,,,,,,,,.
(2)规则1:由(1)可知,至少有一次是“6”的情况有5种,
∴小红赢的概率是(至少有一次是“6”),小莉赢的概率是.
∵,
∴此规则小红获胜的概率大.
规则2:卡片上的数字是球上数字的整数倍的有:,,,共4种情况,
∴小红赢的概率是(卡片上的数字是球上数字的整数倍),小莉赢的概率是.
∵,
∴此规则小莉获胜的概率大.
∴小红要想在游戏中获胜,她应该选择规则1.
21.(1)50,补图见解析
(2)15,15
(3)220人
【分析】本题考查扇形统计图,条形统计图,中位数、众数以及样本估计总体,
(1)从两个统计图中可知,样本中“捐款为5元”的学生有8人,占调查人数的,根据频率可求出答案;
(2)根据众数、中位数的定义进行计算即可;
(3)求出样本捐款金额超过15元(不含15元)的所占百分比,估计总体中捐款金额超过15元(不含15元)人数.
【详解】(1)解: (人,
“捐款为15元”的学生有(人,补全条形统计图如下:
(2)学生捐款金额出现次数最多的是15元,共出现18次,因此捐款金额的众数是15元,
将这50名学生捐款金额从小到大排列处在中间位置的两个数都是15元,因此中位数是15元,
故答案为:15,15;
(3)捐款金额超过15元(不含15元)的人数(人),
所以全校八年级学生为1100名,捐款金额超过15元(不含15元)的人数为220人,
22.(1)见解析
(2)或
【分析】本题主要考查一元二次方程的判别式以及根与系数的关系,熟练掌握根与系数的关系是解题的关键.
(1)根据根的判别式证明即可;
(2)由根与系数的关系求出的值即可得到答案.
【详解】(1)证明:由题意化简得
无论取和值,总有,
故无论取何值,方程都有两个不相等的实数解;
(2)解:由根与系数的关系,得,
,
,
,
,
解得.
23.(1)
(2)
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)设月平均增长率是,利用月份的销售量月份的销售量(月平均增长率),即可得出关于的一元二次方程,解之取其正值即可;
(2)设售价应降低元,则每件的销售利润为元,每天的销售量为件,利用每天的利润每件的销售利润日销售量,即可得出关于的一元二次方程,再结合要尽量减少库存,即可求解.
【详解】(1)设月平均增长率是,
根据题意得:,
解得:,(不符合题意,舍去),
月平均增长率是;
(2)设售价应降低元,则每件的销售利润为元,每天的销售量为件,
依据题意得:,
即,
解得:,,
要尽量减少库存,
,
售价应降低元.
24.(1)证明见解析
(2)
【分析】本题考查了圆周角定理,垂径定理,勾股定理,圆心角、弧、弦的关系,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)由圆周角定理可得,由点为的中点得出,从而得到,即可得证;
(2)由垂径定理可得,设半径为,在中,由勾股定理得,,求出半径,得出,最后由勾股定理进行计算即可.
【详解】(1)证明:是的直径,
∴,
∵点为的中点,
∴,
∴,
∴;
(2)解:∵,,
∴,
设半径为,在中,由勾股定理得,,
解得:,
∴,
∵,
∴.
25.(1)见解析
(2)图中阴影部分的面积为;
(3)①;②
【分析】(1)由可得,从而由可证明;
(2)过D作于H,由,可得,即知,,故,即得;
(3)①连接,过M作于E,根据直径,弦,可得是等边三角形,而M是的中点,即知,即得当最大时,最小,而是等边三角形,即可得点M到的距离的最小值是;
②根据,知M的轨迹是以O为圆心,为半径的弧,当C与A重合时,,即可得,故点M的运动路径长为.
【详解】(1)证明:∵,
∴,
∵,
∴,即,
在和中,
,
∴;
(2)解:过D作于H,如图:
∵半圆O中,直径,
∴,
∵,
∴,
∴,
∴,,
∴;
答:阴影部分面积是;
(3)解:①连接,过M作于E,如图:
∵直径,弦,
∴,
∴是等边三角形,
∵M是的中点,
∴,
∴,
∴,
∴当最大时,最小,
而当C与A重合(或D与B重合)时,最大,如图:
∵是等边三角形,M是的中点,
∴,
∴,
即点M到的距离的最小值是,
故答案为:;
②如图,
由①知:,M的轨迹是以O为圆心,为半径的弧,
当C与A重合时,,
同理,当D与B重合时,,
∴,
∴点M的运动路径长为,
故答案为:.
【点睛】本题考查圆的综合应用,涉及全等三角形的判定,圆的性质及圆中的相关计算,解题的关键是掌握M点的轨迹是以O为圆心,为半径的弧.
26.(1)见解析
(2)见解析
(3)见解析
【分析】本题主要考查了角平分线的定义,平行线的性质与判定,圆切线的判定,直径所对的圆周角是直角,等腰三角形的性质等等,解题的关键在于能够熟练掌握相关知识进行求解.
(1)如图,连接,由,得到,则是圆O的直径,可以推出,由平分,得到,则 ,可证,由此即可证明;
(2)由,,推出,再由,,即可得到,则平分.
(3)连结DE,先根据AAS证明,再由全等三角形的对应边相等即可得出.
【详解】(1)解:如图,连接.
,
是圆的直径,
,
平分,
,
,
,
是的切线.
(2)解:∵,
∴,
∵,
∴,
∴,
∴平分.
(3)解:如图,连结.
是的平分线,于,于,
.
,,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
