第九章 不等式与不等式组 章末复习 讲练课件 74张PPT 2023-2024学年人教版数学七年级下册
文档属性
| 名称 | 第九章 不等式与不等式组 章末复习 讲练课件 74张PPT 2023-2024学年人教版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 08:09:42 | ||
图片预览










文档简介
(共74张PPT)
第九章 不等式与不等式组
第10课 不等式与不等式组章末复习
数学(RJ版) 七年级下册
>
>
>
<
<
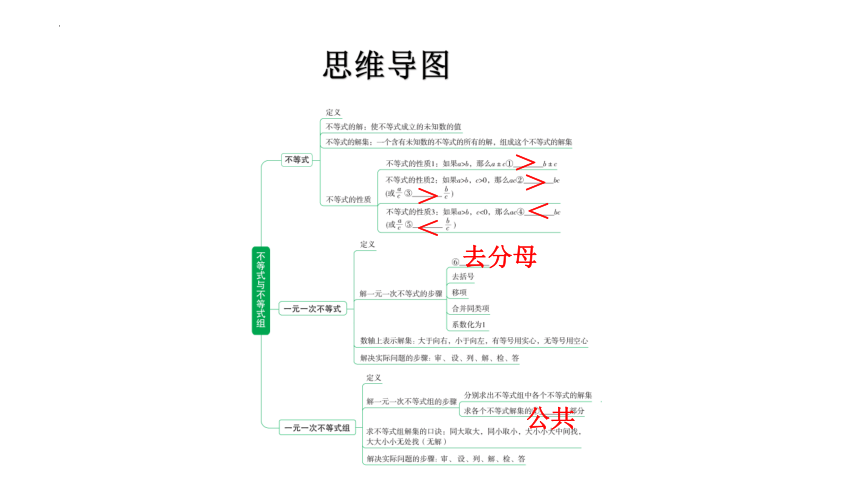
去分母
公共
思维导图
不等式的性质
1. 若a>b,则下列不等式变形不一定成立的是( B )
A. a-1>b-1 B. ac2>bc2
C. -a<-b D. >
B
高频考点
2. 【教材P120习题T6改编】设a>b,用“<”或“>”填空:
(1)2a+5 2b+5;
(2)- a-1 - b-1.
>
<
3. 若不等式(m+2)x>m+2的解集是x<1,则m的取值范围是
( D )
A. m>0 B. m<0
C. m>-2 D. m<-2
D
解一元一次不等式(组)
4. 不等式2x+3≥1的解集在数轴上表示为( C )
A. B.
C. D.
C
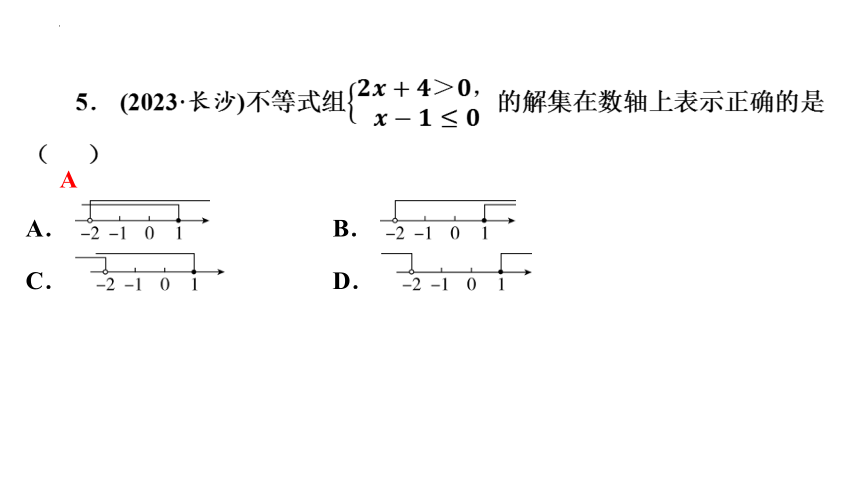
5. (2023·长沙)不等式组的解集在数轴上表示正确的是
( A )
A. B.
C. D.
A
6. 解不等式2(x+1)-1≥4x+2,并将其解集在数轴上表示出来.
解:去括号,得2x+2-1≥4x+2.
移项、合并同类项,得-2x≥1.
系数化为1,得x≤- .
不等式的解集在数轴上表示如图所示.
7. 解不等式组:
解:解不等式①,得x<6.
解不等式②,得x≥-7.
不等式①和②的解集在数轴上表示如图所示.
∴不等式组的解集是-7≤x<6.
8. 不等式组的最小整数解是 .
3
一元一次不等式(组)的应用
9. 小明用30元购买铅笔和签字笔,已知铅笔和签字笔的单价分别是
2元和5元,他买了2支铅笔后,最多还能买几支签字笔?设小明还能买x
支签字笔,则下列不等关系正确的是( D )
A. 5×2+2x≥30 B. 5×2+2x≤30
C. 2×2+5x≥30 D. 2×2+5x≤30
D
10. (2023·广东)某商品进价4元,标价5元出售,商家准备打折销
售,但其利润率不能少于10%,则最多可打 折.
11. (2023·深圳市期中)安排学生住宿,若每间住3人,则还有13人无
房可住;若每间住6人,则还有一间不空也不满.则宿舍的房间数量可能
为 .
8.8
5或6
12. (2023·黄冈)创建文明城市,构建美好家园.为提高垃圾分类意
识,幸福社区决定采购A,B两种型号的新型垃圾桶.若购买3个A型垃圾
桶和4个B型垃圾桶共需要580元,购买6个A型垃圾桶和5个B型垃圾桶共
需要860元.
(1)求两种型号垃圾桶的单价;
解:(1)设A,B两种型号垃圾桶的单价分别为x元和y元.
由题意,得解得
答:A,B两种型号垃圾桶的单价分别为60元和100元.
(2)若需购买A,B两种型号的垃圾桶共200个,总费用不超过15 000
元,至少需购买A型垃圾桶多少个?
解:(2)设购买A型垃圾桶a个,则购买B型垃圾桶(200-a)个.
由题意,得60a+100(200-a)≤15 000.解得a≥125.
答:至少需购买A型垃圾桶125个.
1. 若(m-2)xm2-3-2≥7是关于x的一元一次不等式,则m= .
-2
综合提升
2. 下列不等式变形中,一定正确的是( C )
A. 若ac>bc,则a>b
B. 若a>b,则a|m|>b|m|
C. 若a|c|>b|c|,则a>b
D. 若m>n,则->-
C
3. 用求差法比较大小,就是根据两数之差是正数、负数或0,判断
两数大小关系的方法.若a>b,m小关系为( C )
A. PB. P=Q
C. P>Q
D. P与Q的大小不确定
C
4. 不等式2x-1A. 1个 B. 2个 C. 3个 D. 4个
A
5. 已知关于x的不等式组的解集为x≥15,则所有满
足条件的正整数a的值之和是 .
【解析】解 >x+a,得x>2a+5.解 ≤-3,得x≥15.
∵不等式组的解集为x≥15,∴2a+5<15.解得a<5.
∵a是正整数,∴a可取1,2,3,4.
∴所有满足条件的正整数a的值之和为1+2+3+4=10.
10
6. 解不等式组:并求出它的整数解.
解:解不等式①,得x≤2.
解不等式②,得x>-1.
∴不等式组的解集为-1∴不等式组的整数解为0,1,2.
7. 已知关于x,y的方程组的解都为正数.
(1)求a的取值范围;
解:(1)解方程组得
∵该方程组的解都是正数,∴
∴a>1.
(2)已知a+b=4,且b>0,z=2a-3b,求z的取值范围.
解:(2)∵a+b=4,∴a=4-b.
∴解得0<b<3.
∴z=2a-3b=2(4-b)-3b=8-5b.
∵-15<-5b<0,∴-7<8-5b<8.
∴z的取值范围是-7<z<8.
8. (2023·广安)“广安盐皮蛋”是小平故里的名优特产,某超市销售
A,B两种品牌的盐皮蛋,若购买9箱A种盐皮蛋和6箱B种盐皮蛋共需390
元;若购买5箱A种盐皮蛋和8箱B种盐皮蛋共需310元.
(1)A种盐皮蛋、B种盐皮蛋每箱价格分别是多少元?
解:(1)设A种盐皮蛋每箱价格是x元,B种盐皮蛋每箱价格是y元.
由题意,得解得
答:A种盐皮蛋每箱价格是30元,B种盐皮蛋每箱价格是20元.
(2)若某公司购买A,B两种盐皮蛋共30箱,且A种的数量至少比B种
的数量多5箱,又不超过B种的2倍,怎样购买才能使总费用最少?并求出
最少费用.
(2)设购买A种盐皮蛋m箱,则购买B种盐皮蛋(30-m)箱.
由题意,得解得 ≤m≤20.
∵m为正整数,∴m所有可能的取值为18,19,20.
①当m=18时,30-m=12,购买总费用为30×18+20×12=780(元);
②当m=19时,30-m=11,购买总费用为30×19+20×11=790(元);
③当m=20时,30-m=10,购买总费用为30×20+20×10=800(元).
∵780<790<800,
∴购买A种盐皮蛋18箱,B种盐皮蛋12箱才能使总费用最少,最少费用为780元.
误用不等式的性质
1. 如果a>b,c<0,那么下列不等式成立的是( D )
A. a+c>b B. a+cC. ac-1>bc-1 D. a(c-1)【易错点拨】解题的关键是熟练运用不等式的性质.因为c<0,所以c-
1<-1<0.
D
易错点拨
未知数因数含有字母时忘记讨论因数的符号
2. 对于习题“若a>b,c为实数,则ac2 bc2.”下面是两位同学的解
法,你认为 (填“琪琪”或“嘉嘉”)的解法正确.
琪琪的解法 解析:∵c2>0,∴在
a>b的两边都乘c2,不
等号的方向不变,得
ac2>bc2. 答案:> 嘉嘉的解法
解析:对c2的取值分类讨论.当c2=0时,在a>b
的两边都乘c2,得ac2=bc2;当c2>0时,在a>b
的两边都乘c2,不等号的方向不变,得ac2>bc2.
综上所述,ac2≥bc2.
答案:≥
嘉嘉
【易错点拨】不等式中的未知数因数含有字母时,应先讨论因数是大于
0、等于0或小于0.
在数轴上表示不等式(组)的解集时出错
3. 不等式组的解集在数轴上可表示为( A )
A.
B.
C.
D.
A
【易错点拨】利用不等式的解集在数轴上表示的方法是>,≥向右画;
<,≤向左画.实心是包含等号,空心是不含等号.
去分母时,忽视分数线的括号作用
4. 解不等式 - ≥-1,并把解集在数轴上表示出来.
解:去分母,得2(x-1)-(3x+2)≥-4.
去括号,得2x-2-3x-2≥-4.
移项、合并同类项,得-x≥0.
系数化为1,得x≤0.
不等式的解集在数轴上表示如图所示.
【易错点拨】此题去分母时3x+2容易忘加括号.解不等式时,要注意
分子的整体性,不可忽视分数线的括号作用,特别是去分母时,若分子
是多项式,则必须先添括号,再进行计算.
根据不等式组的解集确定字母的取值范围时出错
5. 若不等式组的解集为x<1,则a的取值范围为 .
6. 若关于x的不等式组无解,则常数b的取值范围是( B )
a≤-1
B
A. b>-3 B. b≥-3 C. b≤-3 D. b<-3
【易错点拨】求出不等式组的解集后,确定字母的取值范围时易遗漏端
点值.
1. 下列式子:①3>0;②4 x +3 y >0;③ x =3;④ x -1≠5;⑤ x +
2<3.其中是不等式的有( C )
A. 2个 B. 3个 C. 4个 D. 5个
C
课堂练习
2. 若 x > y ,则下列式子错误的是( D )
A. x-2>y-2 B. >
C. -2x<-2y D. 1-x>1-y
D
3. 不等式组的解集在数轴上表示为( B )
A. B.
C. D.
B
4. 不等式2 x -1≤5的正整数解的个数有 个.
5. 若关于 x 的不等式3 x -2 a <-2的解集如图所示,则 a = .
3
-2
6. 解不等式: ≤1- .
解:去分母,得2( x +1)≤6-( x -14).
去括号,得2 x +2≤6- x +14.
移项,得2 x + x ≤6+14-2.
合并同类项,得3 x ≤18.
系数化为1,得 x ≤6.
7. 解不等式组:
解:解不等式①,得 x ≥-3.
解不等式②,得 x <1.
∴不等式组的解集为-3≤ x <1.
8. 已知关于 x , y 的方程组的解满足不等式 x
- y >2,则 m 的取值范围为 .
9. 若不等式组的解集为3≤ x ≤4,则 a + b = .
m <-1
1
10. 某市正在创建“全国文明城市”,育才学校拟举办“创文知
识”抢答赛,欲购买 A , B 两种奖品以鼓励抢答者.若购买 A 种20件, B
种15件,则共需380元;若购买 A 种15件, B 种10件,则共需280元.
(1) A , B 两种奖品每件各多少元?
解:(1)设 A 种奖品每件 x 元, B 种奖品每件 y 元.
根据题意,得解得
答: A 种奖品每件16元, B 种奖品每件4元.
(2)现要购买 A , B 两种奖品共100件.
①若购买金额不超过900元,则 A 种奖品最多购买多少件?
(2)①设 A 种奖品购买 a 件,则 B 种奖品购买(100- a )件.
根据题意,得16 a +4(100- a )≤900.解得 a ≤ .
∵ a 为整数,∴ a ≤41.
答: A 种奖品最多购买41件.
②若购买金额不低于860元且不超过900元,则有哪几种购买方案?
②设 A 种奖品购买 b 件,则 B 种奖品购买(100- b )件.
根据题意,得860≤16 b +4(100- b )≤900.解得 ≤ b ≤ .
∵ b 为整数,∴ b 的取值可以是39,40,41.
此时100- b 分别为61,60,59.
∴共有三种购买方案.
方案1: A 种奖品购买39件, B 种奖品购买61件;
方案2: A 种奖品购买40件, B 种奖品购买60件;
方案3: A 种奖品购买41件, B 种奖品购买59件.
不等式的相关概念
1. 给出下列各式:①-3<0;② a + b ;③ x =5;(④ ) - xy + y
2;⑤ x +2> y -7;⑥ a ≠3.其中不等式的个数是( C )
A. 5 B. 4 C. 3 D. 2
C
考点训练
2. 若2 x 2 m -1-8>5是一元一次不等式,则 m 的值为 .
3. 下列不等式中,4,5,6都是它的解的是( B )
A. 2x+1>10 B. 2x+1≥9
C. x+5≤10 D. 3-x>-2
1
B
不等式的性质
4. 若 a > b ,则下列不等式错误的是( C )
A. a+2>b+2 B. a-3>b-3
C. -4a>-4b D. a>b
C
5. 若 x > y ,则8-5 x 8-5 y .(填“>”“<”或“=”)
6. 由不等式 a > b 得到 am < bm 的条件是 m 0.(填“>”“<”或
“=”)
<
<
7. 下列判断不正确的是( C )
A. 若a>b,则-4a<-4b
B. 若2a>3a,则a<0
C. 若a>b,则ac2>bc2
D. 若ac2>bc2,则a>b
C
解一元一次不等式(组)
8. 不等式3 x <6的解集在数轴上表示正确的是( B )
A. B.
C. D.
B
9. 不等式组的解集为 .
10. 已知关于 x 的不等式组则 x 的整数解的和为 .
-3< x ≤1
0
11. 解下列不等式:
(1)6 x -6≤2( x +3);
解:去括号,得6 x -6≤2 x +6.
移项,得6 x -2 x ≤6+6.
合并同类项,得4 x ≤12.
系数化为1,得 x ≤3.
(2) -1< .
解:去分母,得 x +5-8<4(3 x +2).
去括号,得 x +5-8<12 x +8.
移项,得 x -12 x <8+8-5.
合并同类项,得-11 x <11.
系数化为1,得 x >-1.
12. 解不等式组:并把解集在数轴上表示出来.
解:
解不等式①,得 x ≥-1.
解不等式②,得 x <2.
∴不等式组的解集为-1≤ x <2.
不等式组的解集在数轴上表示如图所示.
一元一次不等式(组)的应用
13. 太原古县城2023年(第二届)万人徒步活动于4月22日正式启动,
此次大会以“重走古晋阳·再踏新征程”为主题,全程5 500米,整个行程
环绕太原古县城,途经多个景点.某天,王爷爷为熟悉活动路线,他沿
活动路线先以60米/分钟的平均速度行走了半小时,路过某景点后,加快
了速度.若王爷爷走完全程的时间少于80分钟,则他后半程的平均速度 x
(米/分钟)满足的不等式为( A )
A
A. 60×30+(80-30)x>5 500 B. 60×30+(80-30)x≥5 500
C. 60×30+(80-30)x<5 500 D. 60×30+(80-30)x≤5 500
14. 七(3)班组织数学文化知识竞赛,共设20道选择题,各题分值相
同,答对一题得5分,不答得1分,答错扣2分.在前10道题中,孙华同学
答对8题,1题放弃不答,1题答错,若后面10题都作答,孙华同学的得分
不低于79分,则他至少要再答对( D )
A. 6题 B. 7题
C. 8题 D. 9题
D
15. 某公司组织员工去公园划船,报名人数不足50人,在安排乘船
时发现,每只船坐6人,就剩下18人无船可乘;每只船坐10人,其余的船
坐满后有一只船不空也不满,参加划船的员工共有( A )
A. 48人 B. 45人 C. 44人 D. 42人
A
16. 在罗定市创建广东省县级文明城市活动中,某小区积极响应,
决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,已知购买1个温馨提
示牌和2个垃圾箱共需350元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元;
解:(1)设温馨提示牌的单价是 x 元,垃圾箱的单价是 y 元.
根据题意,得解得
答:温馨提示牌的单价是50元,垃圾箱的单价是150元.
(2)如果需要购买温馨提示牌和垃圾箱共100个,且费用不超过10 000
元,问:最多购买垃圾箱多少个?
解:(2)设购买 m 个垃圾箱,则购买(100- m )个温馨提示牌.
根据题意,得150 m +50(100- m )≤10 000.解得 m ≤50.
因为 m 为正整数,所以 m 的最大整数值为50.
答:最多购买垃圾箱50个.
17. 若 a > b ,则下列式子中一定成立的是( D )
A. a-2C. -a>-b D. >
D
核心考题
18. 当 x 时,式子2 x +4的值为负数.
<-2
19. 不等式6-4 x ≥3 x -8的非负整数解有( B )
A. 2个 B. 3个
C. 4个 D. 5个
B
20. 不等式组的解集在数轴上表示为( A )
A.
B.
C.
D.
A
21. 不等式组的整数解的个数是( B )
A. 1 B. 2 C. 3 D. 4
B
22. 若关于 x 的不等式组的解集是 x > a ,则( B )
A. a>2 B. a≥2
C. a<2 D. a≤2
B
23. 某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到
敬老院慰问老人.如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果
分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1
盒.这个敬老院的老人最少有( B )
A. 29人 B. 30人 C. 31人 D. 32人
B
24. 解不等式 -1≤ ,并把解集在数轴上表示出来.
解:去分母,得 x -1-6≤3 x .
移项、合并同类项,得-2 x ≤7.
系数化为1,得 x ≥- .
不等式的解集在数轴上表示如图所示.
25. 解不等式组:并在数轴上表示解集.
解:解不等式①,得 x ≥-1.
解不等式②,得 x <2.
∴不等式组的解集为-1≤ x <2.
不等式组的解集在数轴上表示如图所示.
26. x 取哪些整数值时,不等式 x +3>6与2 x -1≤10都成立?
解:解不等式 x +3>6,得 x >3.
解不等式2 x -1≤10,得 x ≤5.5.
∴3< x ≤5.5.
∴满足条件的整数有4,5.
27. 沙棘是一种耐旱、固沙的植物,被广泛用于水土保持.某市地
处沙漠边沿,为了防止土地荒漠化,该市原计划2011年到2021年每年种
植30公顷沙棘,2018年之前都按原计划种植,后来的年种植量比原计划
增加了,且后来的种植总面积不低于前几年的种植总面积,后来的年种
植量至少比原计划增加多少公顷?
解:设后来的年种植量为 x 公顷.
依题意,得4 x ≥7×30.解得 x ≥52.5.
∴后来的年种植量至少为52.5公顷.
∴52.5-30=22.5(公顷).
答:后来的年种植量至少比原计划增加22.5公顷.
28. 已知方程组的解满足 x 为非正数, y 为
负数.
(1)求 m 的取值范围;
解:(1)解方程组得
∵方程组的解满足 x 为非正数, y 为负数,∴
解得- < m ≤2.
∴ m 的取值范围为- < m ≤2.
(2)化简:| m -3|-| m +2|;
(3)在第(1)小题的取值范围内,当 m 为何整数时,不等式(2 m -1) x <2
m -1的解集为 x >1
(2)∵- < m ≤2,∴ m -3<0, m +2>0.
∴| m -3|-| m +2|=-( m -3)-( m +2)=-2 m +1.
(3)∵不等式(2 m -1) x <2 m -1的解集为 x >1,∴2 m -1<0.
解得 m < .∴- < m < .
∵ m 为整数,∴ m =0.
∴ m 可取的整数值为0.
29. 为了丰富学生的课余生活,某校计划购买足球和篮球给同学们
活动使用,若购买1个足球和2个篮球需用220元;若购买2个足球和1个篮
球需用230元.
(1)求购买一个足球和一个篮球各多少元;
解:(1)设购买一个足球需 x 元,购买一个篮球需 y 元.
依题意,得解得
答:购买一个足球需80元,一个篮球需70元.
(2)如果购买足球和篮球共75个,且购买足球的数量不低于篮球数量
的1.4倍,求最多可购买多少个篮球?
(2)设购买篮球 m 个,则购买足球(75- m )个.
根据题意,得75- m ≥1.4 m .解得 m ≤31.25.
∵ m 为整数,∴ m 最大取31.
答:最多可购买31个篮球.
(3)学校根据实际情况,在(2)的前提下,要求购买的总费用不超过5
700元,请问有哪几种购买方案?哪种方案最省钱?
(3)根据题意,得70 m +80(75- m )≤5 700.解得 m ≥30.
由(2),得 m ≤31.25.∴30≤ m ≤31.25.
∵ m 为正整数,∴ m 可取30,31.
∴有两种购买方案:
方案一:购买篮球30个,购买足球45个;
方案二:购买篮球31个,购买足球44个.
∴方案一的总费用为30×70+45×80=5 700(元);
方案二的总费用为31×70+44×80=5 690(元).
∵5 690<5 700,∴方案二最省钱.
第九章 不等式与不等式组
第10课 不等式与不等式组章末复习
数学(RJ版) 七年级下册
>
>
>
<
<
去分母
公共
思维导图
不等式的性质
1. 若a>b,则下列不等式变形不一定成立的是( B )
A. a-1>b-1 B. ac2>bc2
C. -a<-b D. >
B
高频考点
2. 【教材P120习题T6改编】设a>b,用“<”或“>”填空:
(1)2a+5 2b+5;
(2)- a-1 - b-1.
>
<
3. 若不等式(m+2)x>m+2的解集是x<1,则m的取值范围是
( D )
A. m>0 B. m<0
C. m>-2 D. m<-2
D
解一元一次不等式(组)
4. 不等式2x+3≥1的解集在数轴上表示为( C )
A. B.
C. D.
C
5. (2023·长沙)不等式组的解集在数轴上表示正确的是
( A )
A. B.
C. D.
A
6. 解不等式2(x+1)-1≥4x+2,并将其解集在数轴上表示出来.
解:去括号,得2x+2-1≥4x+2.
移项、合并同类项,得-2x≥1.
系数化为1,得x≤- .
不等式的解集在数轴上表示如图所示.
7. 解不等式组:
解:解不等式①,得x<6.
解不等式②,得x≥-7.
不等式①和②的解集在数轴上表示如图所示.
∴不等式组的解集是-7≤x<6.
8. 不等式组的最小整数解是 .
3
一元一次不等式(组)的应用
9. 小明用30元购买铅笔和签字笔,已知铅笔和签字笔的单价分别是
2元和5元,他买了2支铅笔后,最多还能买几支签字笔?设小明还能买x
支签字笔,则下列不等关系正确的是( D )
A. 5×2+2x≥30 B. 5×2+2x≤30
C. 2×2+5x≥30 D. 2×2+5x≤30
D
10. (2023·广东)某商品进价4元,标价5元出售,商家准备打折销
售,但其利润率不能少于10%,则最多可打 折.
11. (2023·深圳市期中)安排学生住宿,若每间住3人,则还有13人无
房可住;若每间住6人,则还有一间不空也不满.则宿舍的房间数量可能
为 .
8.8
5或6
12. (2023·黄冈)创建文明城市,构建美好家园.为提高垃圾分类意
识,幸福社区决定采购A,B两种型号的新型垃圾桶.若购买3个A型垃圾
桶和4个B型垃圾桶共需要580元,购买6个A型垃圾桶和5个B型垃圾桶共
需要860元.
(1)求两种型号垃圾桶的单价;
解:(1)设A,B两种型号垃圾桶的单价分别为x元和y元.
由题意,得解得
答:A,B两种型号垃圾桶的单价分别为60元和100元.
(2)若需购买A,B两种型号的垃圾桶共200个,总费用不超过15 000
元,至少需购买A型垃圾桶多少个?
解:(2)设购买A型垃圾桶a个,则购买B型垃圾桶(200-a)个.
由题意,得60a+100(200-a)≤15 000.解得a≥125.
答:至少需购买A型垃圾桶125个.
1. 若(m-2)xm2-3-2≥7是关于x的一元一次不等式,则m= .
-2
综合提升
2. 下列不等式变形中,一定正确的是( C )
A. 若ac>bc,则a>b
B. 若a>b,则a|m|>b|m|
C. 若a|c|>b|c|,则a>b
D. 若m>n,则->-
C
3. 用求差法比较大小,就是根据两数之差是正数、负数或0,判断
两数大小关系的方法.若a>b,m
A. P
C. P>Q
D. P与Q的大小不确定
C
4. 不等式2x-1
A
5. 已知关于x的不等式组的解集为x≥15,则所有满
足条件的正整数a的值之和是 .
【解析】解 >x+a,得x>2a+5.解 ≤-3,得x≥15.
∵不等式组的解集为x≥15,∴2a+5<15.解得a<5.
∵a是正整数,∴a可取1,2,3,4.
∴所有满足条件的正整数a的值之和为1+2+3+4=10.
10
6. 解不等式组:并求出它的整数解.
解:解不等式①,得x≤2.
解不等式②,得x>-1.
∴不等式组的解集为-1
7. 已知关于x,y的方程组的解都为正数.
(1)求a的取值范围;
解:(1)解方程组得
∵该方程组的解都是正数,∴
∴a>1.
(2)已知a+b=4,且b>0,z=2a-3b,求z的取值范围.
解:(2)∵a+b=4,∴a=4-b.
∴解得0<b<3.
∴z=2a-3b=2(4-b)-3b=8-5b.
∵-15<-5b<0,∴-7<8-5b<8.
∴z的取值范围是-7<z<8.
8. (2023·广安)“广安盐皮蛋”是小平故里的名优特产,某超市销售
A,B两种品牌的盐皮蛋,若购买9箱A种盐皮蛋和6箱B种盐皮蛋共需390
元;若购买5箱A种盐皮蛋和8箱B种盐皮蛋共需310元.
(1)A种盐皮蛋、B种盐皮蛋每箱价格分别是多少元?
解:(1)设A种盐皮蛋每箱价格是x元,B种盐皮蛋每箱价格是y元.
由题意,得解得
答:A种盐皮蛋每箱价格是30元,B种盐皮蛋每箱价格是20元.
(2)若某公司购买A,B两种盐皮蛋共30箱,且A种的数量至少比B种
的数量多5箱,又不超过B种的2倍,怎样购买才能使总费用最少?并求出
最少费用.
(2)设购买A种盐皮蛋m箱,则购买B种盐皮蛋(30-m)箱.
由题意,得解得 ≤m≤20.
∵m为正整数,∴m所有可能的取值为18,19,20.
①当m=18时,30-m=12,购买总费用为30×18+20×12=780(元);
②当m=19时,30-m=11,购买总费用为30×19+20×11=790(元);
③当m=20时,30-m=10,购买总费用为30×20+20×10=800(元).
∵780<790<800,
∴购买A种盐皮蛋18箱,B种盐皮蛋12箱才能使总费用最少,最少费用为780元.
误用不等式的性质
1. 如果a>b,c<0,那么下列不等式成立的是( D )
A. a+c>b B. a+c
1<-1<0.
D
易错点拨
未知数因数含有字母时忘记讨论因数的符号
2. 对于习题“若a>b,c为实数,则ac2 bc2.”下面是两位同学的解
法,你认为 (填“琪琪”或“嘉嘉”)的解法正确.
琪琪的解法 解析:∵c2>0,∴在
a>b的两边都乘c2,不
等号的方向不变,得
ac2>bc2. 答案:> 嘉嘉的解法
解析:对c2的取值分类讨论.当c2=0时,在a>b
的两边都乘c2,得ac2=bc2;当c2>0时,在a>b
的两边都乘c2,不等号的方向不变,得ac2>bc2.
综上所述,ac2≥bc2.
答案:≥
嘉嘉
【易错点拨】不等式中的未知数因数含有字母时,应先讨论因数是大于
0、等于0或小于0.
在数轴上表示不等式(组)的解集时出错
3. 不等式组的解集在数轴上可表示为( A )
A.
B.
C.
D.
A
【易错点拨】利用不等式的解集在数轴上表示的方法是>,≥向右画;
<,≤向左画.实心是包含等号,空心是不含等号.
去分母时,忽视分数线的括号作用
4. 解不等式 - ≥-1,并把解集在数轴上表示出来.
解:去分母,得2(x-1)-(3x+2)≥-4.
去括号,得2x-2-3x-2≥-4.
移项、合并同类项,得-x≥0.
系数化为1,得x≤0.
不等式的解集在数轴上表示如图所示.
【易错点拨】此题去分母时3x+2容易忘加括号.解不等式时,要注意
分子的整体性,不可忽视分数线的括号作用,特别是去分母时,若分子
是多项式,则必须先添括号,再进行计算.
根据不等式组的解集确定字母的取值范围时出错
5. 若不等式组的解集为x<1,则a的取值范围为 .
6. 若关于x的不等式组无解,则常数b的取值范围是( B )
a≤-1
B
A. b>-3 B. b≥-3 C. b≤-3 D. b<-3
【易错点拨】求出不等式组的解集后,确定字母的取值范围时易遗漏端
点值.
1. 下列式子:①3>0;②4 x +3 y >0;③ x =3;④ x -1≠5;⑤ x +
2<3.其中是不等式的有( C )
A. 2个 B. 3个 C. 4个 D. 5个
C
课堂练习
2. 若 x > y ,则下列式子错误的是( D )
A. x-2>y-2 B. >
C. -2x<-2y D. 1-x>1-y
D
3. 不等式组的解集在数轴上表示为( B )
A. B.
C. D.
B
4. 不等式2 x -1≤5的正整数解的个数有 个.
5. 若关于 x 的不等式3 x -2 a <-2的解集如图所示,则 a = .
3
-2
6. 解不等式: ≤1- .
解:去分母,得2( x +1)≤6-( x -14).
去括号,得2 x +2≤6- x +14.
移项,得2 x + x ≤6+14-2.
合并同类项,得3 x ≤18.
系数化为1,得 x ≤6.
7. 解不等式组:
解:解不等式①,得 x ≥-3.
解不等式②,得 x <1.
∴不等式组的解集为-3≤ x <1.
8. 已知关于 x , y 的方程组的解满足不等式 x
- y >2,则 m 的取值范围为 .
9. 若不等式组的解集为3≤ x ≤4,则 a + b = .
m <-1
1
10. 某市正在创建“全国文明城市”,育才学校拟举办“创文知
识”抢答赛,欲购买 A , B 两种奖品以鼓励抢答者.若购买 A 种20件, B
种15件,则共需380元;若购买 A 种15件, B 种10件,则共需280元.
(1) A , B 两种奖品每件各多少元?
解:(1)设 A 种奖品每件 x 元, B 种奖品每件 y 元.
根据题意,得解得
答: A 种奖品每件16元, B 种奖品每件4元.
(2)现要购买 A , B 两种奖品共100件.
①若购买金额不超过900元,则 A 种奖品最多购买多少件?
(2)①设 A 种奖品购买 a 件,则 B 种奖品购买(100- a )件.
根据题意,得16 a +4(100- a )≤900.解得 a ≤ .
∵ a 为整数,∴ a ≤41.
答: A 种奖品最多购买41件.
②若购买金额不低于860元且不超过900元,则有哪几种购买方案?
②设 A 种奖品购买 b 件,则 B 种奖品购买(100- b )件.
根据题意,得860≤16 b +4(100- b )≤900.解得 ≤ b ≤ .
∵ b 为整数,∴ b 的取值可以是39,40,41.
此时100- b 分别为61,60,59.
∴共有三种购买方案.
方案1: A 种奖品购买39件, B 种奖品购买61件;
方案2: A 种奖品购买40件, B 种奖品购买60件;
方案3: A 种奖品购买41件, B 种奖品购买59件.
不等式的相关概念
1. 给出下列各式:①-3<0;② a + b ;③ x =5;(④ ) - xy + y
2;⑤ x +2> y -7;⑥ a ≠3.其中不等式的个数是( C )
A. 5 B. 4 C. 3 D. 2
C
考点训练
2. 若2 x 2 m -1-8>5是一元一次不等式,则 m 的值为 .
3. 下列不等式中,4,5,6都是它的解的是( B )
A. 2x+1>10 B. 2x+1≥9
C. x+5≤10 D. 3-x>-2
1
B
不等式的性质
4. 若 a > b ,则下列不等式错误的是( C )
A. a+2>b+2 B. a-3>b-3
C. -4a>-4b D. a>b
C
5. 若 x > y ,则8-5 x 8-5 y .(填“>”“<”或“=”)
6. 由不等式 a > b 得到 am < bm 的条件是 m 0.(填“>”“<”或
“=”)
<
<
7. 下列判断不正确的是( C )
A. 若a>b,则-4a<-4b
B. 若2a>3a,则a<0
C. 若a>b,则ac2>bc2
D. 若ac2>bc2,则a>b
C
解一元一次不等式(组)
8. 不等式3 x <6的解集在数轴上表示正确的是( B )
A. B.
C. D.
B
9. 不等式组的解集为 .
10. 已知关于 x 的不等式组则 x 的整数解的和为 .
-3< x ≤1
0
11. 解下列不等式:
(1)6 x -6≤2( x +3);
解:去括号,得6 x -6≤2 x +6.
移项,得6 x -2 x ≤6+6.
合并同类项,得4 x ≤12.
系数化为1,得 x ≤3.
(2) -1< .
解:去分母,得 x +5-8<4(3 x +2).
去括号,得 x +5-8<12 x +8.
移项,得 x -12 x <8+8-5.
合并同类项,得-11 x <11.
系数化为1,得 x >-1.
12. 解不等式组:并把解集在数轴上表示出来.
解:
解不等式①,得 x ≥-1.
解不等式②,得 x <2.
∴不等式组的解集为-1≤ x <2.
不等式组的解集在数轴上表示如图所示.
一元一次不等式(组)的应用
13. 太原古县城2023年(第二届)万人徒步活动于4月22日正式启动,
此次大会以“重走古晋阳·再踏新征程”为主题,全程5 500米,整个行程
环绕太原古县城,途经多个景点.某天,王爷爷为熟悉活动路线,他沿
活动路线先以60米/分钟的平均速度行走了半小时,路过某景点后,加快
了速度.若王爷爷走完全程的时间少于80分钟,则他后半程的平均速度 x
(米/分钟)满足的不等式为( A )
A
A. 60×30+(80-30)x>5 500 B. 60×30+(80-30)x≥5 500
C. 60×30+(80-30)x<5 500 D. 60×30+(80-30)x≤5 500
14. 七(3)班组织数学文化知识竞赛,共设20道选择题,各题分值相
同,答对一题得5分,不答得1分,答错扣2分.在前10道题中,孙华同学
答对8题,1题放弃不答,1题答错,若后面10题都作答,孙华同学的得分
不低于79分,则他至少要再答对( D )
A. 6题 B. 7题
C. 8题 D. 9题
D
15. 某公司组织员工去公园划船,报名人数不足50人,在安排乘船
时发现,每只船坐6人,就剩下18人无船可乘;每只船坐10人,其余的船
坐满后有一只船不空也不满,参加划船的员工共有( A )
A. 48人 B. 45人 C. 44人 D. 42人
A
16. 在罗定市创建广东省县级文明城市活动中,某小区积极响应,
决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,已知购买1个温馨提
示牌和2个垃圾箱共需350元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元;
解:(1)设温馨提示牌的单价是 x 元,垃圾箱的单价是 y 元.
根据题意,得解得
答:温馨提示牌的单价是50元,垃圾箱的单价是150元.
(2)如果需要购买温馨提示牌和垃圾箱共100个,且费用不超过10 000
元,问:最多购买垃圾箱多少个?
解:(2)设购买 m 个垃圾箱,则购买(100- m )个温馨提示牌.
根据题意,得150 m +50(100- m )≤10 000.解得 m ≤50.
因为 m 为正整数,所以 m 的最大整数值为50.
答:最多购买垃圾箱50个.
17. 若 a > b ,则下列式子中一定成立的是( D )
A. a-2
D
核心考题
18. 当 x 时,式子2 x +4的值为负数.
<-2
19. 不等式6-4 x ≥3 x -8的非负整数解有( B )
A. 2个 B. 3个
C. 4个 D. 5个
B
20. 不等式组的解集在数轴上表示为( A )
A.
B.
C.
D.
A
21. 不等式组的整数解的个数是( B )
A. 1 B. 2 C. 3 D. 4
B
22. 若关于 x 的不等式组的解集是 x > a ,则( B )
A. a>2 B. a≥2
C. a<2 D. a≤2
B
23. 某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到
敬老院慰问老人.如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果
分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1
盒.这个敬老院的老人最少有( B )
A. 29人 B. 30人 C. 31人 D. 32人
B
24. 解不等式 -1≤ ,并把解集在数轴上表示出来.
解:去分母,得 x -1-6≤3 x .
移项、合并同类项,得-2 x ≤7.
系数化为1,得 x ≥- .
不等式的解集在数轴上表示如图所示.
25. 解不等式组:并在数轴上表示解集.
解:解不等式①,得 x ≥-1.
解不等式②,得 x <2.
∴不等式组的解集为-1≤ x <2.
不等式组的解集在数轴上表示如图所示.
26. x 取哪些整数值时,不等式 x +3>6与2 x -1≤10都成立?
解:解不等式 x +3>6,得 x >3.
解不等式2 x -1≤10,得 x ≤5.5.
∴3< x ≤5.5.
∴满足条件的整数有4,5.
27. 沙棘是一种耐旱、固沙的植物,被广泛用于水土保持.某市地
处沙漠边沿,为了防止土地荒漠化,该市原计划2011年到2021年每年种
植30公顷沙棘,2018年之前都按原计划种植,后来的年种植量比原计划
增加了,且后来的种植总面积不低于前几年的种植总面积,后来的年种
植量至少比原计划增加多少公顷?
解:设后来的年种植量为 x 公顷.
依题意,得4 x ≥7×30.解得 x ≥52.5.
∴后来的年种植量至少为52.5公顷.
∴52.5-30=22.5(公顷).
答:后来的年种植量至少比原计划增加22.5公顷.
28. 已知方程组的解满足 x 为非正数, y 为
负数.
(1)求 m 的取值范围;
解:(1)解方程组得
∵方程组的解满足 x 为非正数, y 为负数,∴
解得- < m ≤2.
∴ m 的取值范围为- < m ≤2.
(2)化简:| m -3|-| m +2|;
(3)在第(1)小题的取值范围内,当 m 为何整数时,不等式(2 m -1) x <2
m -1的解集为 x >1
(2)∵- < m ≤2,∴ m -3<0, m +2>0.
∴| m -3|-| m +2|=-( m -3)-( m +2)=-2 m +1.
(3)∵不等式(2 m -1) x <2 m -1的解集为 x >1,∴2 m -1<0.
解得 m < .∴- < m < .
∵ m 为整数,∴ m =0.
∴ m 可取的整数值为0.
29. 为了丰富学生的课余生活,某校计划购买足球和篮球给同学们
活动使用,若购买1个足球和2个篮球需用220元;若购买2个足球和1个篮
球需用230元.
(1)求购买一个足球和一个篮球各多少元;
解:(1)设购买一个足球需 x 元,购买一个篮球需 y 元.
依题意,得解得
答:购买一个足球需80元,一个篮球需70元.
(2)如果购买足球和篮球共75个,且购买足球的数量不低于篮球数量
的1.4倍,求最多可购买多少个篮球?
(2)设购买篮球 m 个,则购买足球(75- m )个.
根据题意,得75- m ≥1.4 m .解得 m ≤31.25.
∵ m 为整数,∴ m 最大取31.
答:最多可购买31个篮球.
(3)学校根据实际情况,在(2)的前提下,要求购买的总费用不超过5
700元,请问有哪几种购买方案?哪种方案最省钱?
(3)根据题意,得70 m +80(75- m )≤5 700.解得 m ≥30.
由(2),得 m ≤31.25.∴30≤ m ≤31.25.
∵ m 为正整数,∴ m 可取30,31.
∴有两种购买方案:
方案一:购买篮球30个,购买足球45个;
方案二:购买篮球31个,购买足球44个.
∴方案一的总费用为30×70+45×80=5 700(元);
方案二的总费用为31×70+44×80=5 690(元).
∵5 690<5 700,∴方案二最省钱.
