9.3一元一次不等式组的解法(2) 讲练课件 23张PPT 2023-2024学年人教版数学七年级下册
文档属性
| 名称 | 9.3一元一次不等式组的解法(2) 讲练课件 23张PPT 2023-2024学年人教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 779.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第九章 不等式与不等式组
第8课 一元一次不等式组的解法(2)
数学(RJ版) 七年级下册
解较复杂的一元一次不等式组
例1 解不等式组:并把解集在数轴上表示出来.
解:解不等式①,得x>3.
解不等式②,得x≥1.
∴不等式组的解集是x>3.
不等式组的解集在数轴上表示如图所示.
新课学习
1. 解不等式组:并在数轴上表示解集.
解:解不等式①,得x≤2.
解不等式②,得x>-1.
∴不等式组的解集为-1不等式组的解集在数轴上表示如图.
例2 解不等式组:并写出该不等式组的非负
整数解.
解:解不等式①,得x≤1.
解不等式②,得x< .
∴不等式组的解集为x≤1.
∴不等式组的非负整数解为0,1.
2. 解不等式组:并写出它的所有整数解.
解:解不等式①,得x<3.
解不等式②,得x≥-1.
∴不等式组的解集为-1≤x<3.
∴不等式组的整数解为-1,0,1,2.
一元一次不等式组的应用
例3 当x取哪些整数时,不等式5x+1>3(x+1)与 x-5≤3- x都
成立?
解:依题意,得
解不等式①,得x>1.解不等式②,得x≤4.
∴不等式组的解集为1∴x可取的整数值是2,3,4.
3. 当x取哪些整数时,-2≤ +1<3成立?
解:依题意,得
解不等式①,得x≥-4.解不等式②,得x< .
∴不等式组的解集为-4≤x< .
∴x可取的整数值是-4,-3,-2,-1,0,1,2,3.
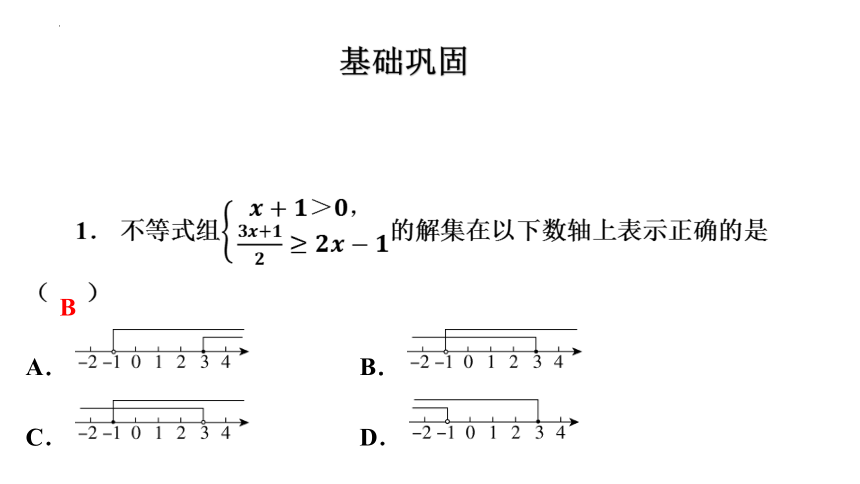
1. 不等式组的解集在以下数轴上表示正确的是
( B )
A. B.
C. D.
B
基础巩固
2. 不等式组的整数解为 2,3 .
2,3
3. 解不等式组:并把解集在数轴上表示
出来.
解:解不等式①,得x>-3.
解不等式②,得x≤2.
∴不等式组的解集为-3不等式组的解集在数轴上表示如图所示.
4. 当x取哪些整数值时,不等式4(x-0.3)<0.5x+5.8与3+x> x+1
都成立?
解:解不等式4(x-0.3)<0.5x+5.8,得x<2.
解不等式3+x> x+1,得x>-4.
∴两个不等式的公共解集为-4<x<2.
∴x可取的整数值是-3,-2,-1,0,1.
5. 一题多问 解不等式组:
(1)当a=1时,请完成下列问题:
(ⅰ)解不等式①,得 x≤1 ;
(ⅱ)解不等式②,得 x>-2 ;
(ⅲ)将不等式①和②的解集在数轴上表示出来;
x≤1
x>-2
(ⅳ)原不等式组的解集为 -2<x≤1 ;
(ⅴ)满足原不等式组的整数解的和为 0 .
解:(1)(ⅲ)将不等式①和②的解集在数轴上表示如图所示.
-2<x≤1
0
(2)若该不等式组的解集为-3<x≤1,则a的值为 .
(3)若该不等式组无解,则a的取值范围为 a≤0 .
(4)【拓展延伸】若该不等式组有且只有4个整数解,求a的取值范
围.
(4)解不等式①,得x≤1.解不等式②,得x>1-3a.
a≤0
∵该不等式组有且只有4个整数解,即1,0,-1,-2,
∴-3≤1-3a<-2.解得1<a≤ .
∴a的取值范围为1<a≤ .
本课复习
1. 解不等式组:并把它的解集表示在数
轴上.
解:解不等式5 x -2>3( x +1),得 x > .
解不等式 x -1≤7- x ,得 x ≤4.
∴不等式组的解集为 < x ≤4.
不等式组的解集表示在数轴上如图.
2. 解不等式组:并把它的解集表示在
数轴上.
解:解不等式2(2 x -1)≤3(1+ x ),得 x ≤5.
解不等式 < x - ,得 x >-1.
∴不等式组的解集为-1< x ≤5.
不等式组的解集表示在数轴上如图.
循环复习
3. 小颖同学准备用26元买笔和笔记本,已知一支笔2元,一本笔记
本3元,他买了5本笔记本,最多还能买多少支笔?设他还能买 x 支笔,则
列出的不等式为( A )
A. 2x+3×5≤26 B. 2x+3×5≥26
C. 3x+2×5≤26 D. 3x+2×5≥26
A
1. 某不等式组的解集在数轴上表示如下,则它的整数解是
.
2. 如果式子7 x -5与-3 x +2的值都小于1,那么 x 的取值范围是
.
-1,
0,1
< x <
课堂练习
3. 一元一次不等式组的解集中,整数解的个数是
( C )
A. 4 B. 5 C. 6 D. 7
C
4. 解不等式组:
解:解不等式①,得 x >1.
解不等式②,得 x <2.
∴不等式组的解集为1< x <2.
5. 解不等式组请结合题意填空,完成本题
的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来;
x ≥-2
x <1
(4)所以原不等式组的解集为 ;
(5)原不等式组的整数解为 .
-2≤ x <1
-2,-1,0
6. 当 x 取哪些整数时,-2≤ <2成立?
解:原不等式组可变形为
解不等式①,得 x ≥- .解不等式②,得 x < .
∴原不等式组的解集为- ≤ x < .
∴ x 可取的整数值为-3,-2,-1,0,1,2.
7. (2023·聊城)若不等式组的解集为 x ≥ m ,则 m 的取
值范围是 .
m ≥-1
8. 已知关于 x , y 的方程组的解满足 x <1, y
<2,求满足条件的 m 的整数值.
解:
①+②,得2 x =-2 m -2.解得 x =- m -1.
①-②,得4 y =6 m -8.解得 y = .
∵ x <1, y <2,∴解得-2< m < .
∴ m 的整数值为-1,0,1,2.
第九章 不等式与不等式组
第8课 一元一次不等式组的解法(2)
数学(RJ版) 七年级下册
解较复杂的一元一次不等式组
例1 解不等式组:并把解集在数轴上表示出来.
解:解不等式①,得x>3.
解不等式②,得x≥1.
∴不等式组的解集是x>3.
不等式组的解集在数轴上表示如图所示.
新课学习
1. 解不等式组:并在数轴上表示解集.
解:解不等式①,得x≤2.
解不等式②,得x>-1.
∴不等式组的解集为-1
例2 解不等式组:并写出该不等式组的非负
整数解.
解:解不等式①,得x≤1.
解不等式②,得x< .
∴不等式组的解集为x≤1.
∴不等式组的非负整数解为0,1.
2. 解不等式组:并写出它的所有整数解.
解:解不等式①,得x<3.
解不等式②,得x≥-1.
∴不等式组的解集为-1≤x<3.
∴不等式组的整数解为-1,0,1,2.
一元一次不等式组的应用
例3 当x取哪些整数时,不等式5x+1>3(x+1)与 x-5≤3- x都
成立?
解:依题意,得
解不等式①,得x>1.解不等式②,得x≤4.
∴不等式组的解集为1
3. 当x取哪些整数时,-2≤ +1<3成立?
解:依题意,得
解不等式①,得x≥-4.解不等式②,得x< .
∴不等式组的解集为-4≤x< .
∴x可取的整数值是-4,-3,-2,-1,0,1,2,3.
1. 不等式组的解集在以下数轴上表示正确的是
( B )
A. B.
C. D.
B
基础巩固
2. 不等式组的整数解为 2,3 .
2,3
3. 解不等式组:并把解集在数轴上表示
出来.
解:解不等式①,得x>-3.
解不等式②,得x≤2.
∴不等式组的解集为-3
4. 当x取哪些整数值时,不等式4(x-0.3)<0.5x+5.8与3+x> x+1
都成立?
解:解不等式4(x-0.3)<0.5x+5.8,得x<2.
解不等式3+x> x+1,得x>-4.
∴两个不等式的公共解集为-4<x<2.
∴x可取的整数值是-3,-2,-1,0,1.
5. 一题多问 解不等式组:
(1)当a=1时,请完成下列问题:
(ⅰ)解不等式①,得 x≤1 ;
(ⅱ)解不等式②,得 x>-2 ;
(ⅲ)将不等式①和②的解集在数轴上表示出来;
x≤1
x>-2
(ⅳ)原不等式组的解集为 -2<x≤1 ;
(ⅴ)满足原不等式组的整数解的和为 0 .
解:(1)(ⅲ)将不等式①和②的解集在数轴上表示如图所示.
-2<x≤1
0
(2)若该不等式组的解集为-3<x≤1,则a的值为 .
(3)若该不等式组无解,则a的取值范围为 a≤0 .
(4)【拓展延伸】若该不等式组有且只有4个整数解,求a的取值范
围.
(4)解不等式①,得x≤1.解不等式②,得x>1-3a.
a≤0
∵该不等式组有且只有4个整数解,即1,0,-1,-2,
∴-3≤1-3a<-2.解得1<a≤ .
∴a的取值范围为1<a≤ .
本课复习
1. 解不等式组:并把它的解集表示在数
轴上.
解:解不等式5 x -2>3( x +1),得 x > .
解不等式 x -1≤7- x ,得 x ≤4.
∴不等式组的解集为 < x ≤4.
不等式组的解集表示在数轴上如图.
2. 解不等式组:并把它的解集表示在
数轴上.
解:解不等式2(2 x -1)≤3(1+ x ),得 x ≤5.
解不等式 < x - ,得 x >-1.
∴不等式组的解集为-1< x ≤5.
不等式组的解集表示在数轴上如图.
循环复习
3. 小颖同学准备用26元买笔和笔记本,已知一支笔2元,一本笔记
本3元,他买了5本笔记本,最多还能买多少支笔?设他还能买 x 支笔,则
列出的不等式为( A )
A. 2x+3×5≤26 B. 2x+3×5≥26
C. 3x+2×5≤26 D. 3x+2×5≥26
A
1. 某不等式组的解集在数轴上表示如下,则它的整数解是
.
2. 如果式子7 x -5与-3 x +2的值都小于1,那么 x 的取值范围是
.
-1,
0,1
< x <
课堂练习
3. 一元一次不等式组的解集中,整数解的个数是
( C )
A. 4 B. 5 C. 6 D. 7
C
4. 解不等式组:
解:解不等式①,得 x >1.
解不等式②,得 x <2.
∴不等式组的解集为1< x <2.
5. 解不等式组请结合题意填空,完成本题
的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来;
x ≥-2
x <1
(4)所以原不等式组的解集为 ;
(5)原不等式组的整数解为 .
-2≤ x <1
-2,-1,0
6. 当 x 取哪些整数时,-2≤ <2成立?
解:原不等式组可变形为
解不等式①,得 x ≥- .解不等式②,得 x < .
∴原不等式组的解集为- ≤ x < .
∴ x 可取的整数值为-3,-2,-1,0,1,2.
7. (2023·聊城)若不等式组的解集为 x ≥ m ,则 m 的取
值范围是 .
m ≥-1
8. 已知关于 x , y 的方程组的解满足 x <1, y
<2,求满足条件的 m 的整数值.
解:
①+②,得2 x =-2 m -2.解得 x =- m -1.
①-②,得4 y =6 m -8.解得 y = .
∵ x <1, y <2,∴解得-2< m < .
∴ m 的整数值为-1,0,1,2.
