2024年中考数学专题练习 圆(含答案)
文档属性
| 名称 | 2024年中考数学专题练习 圆(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 265.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 08:29:05 | ||
图片预览


文档简介
2024年中考数学专题练习——圆
一、单选题
1.一条弦分圆周为5:7,这条弦所对的圆周角为( )
A.75° B.105° C.60°或120° D.75°或105°
2.如图,AB是⊙O的直径, = = ,∠COD=34°,则∠AEO的度数是( )
A.51° B.56° C.68° D.78°
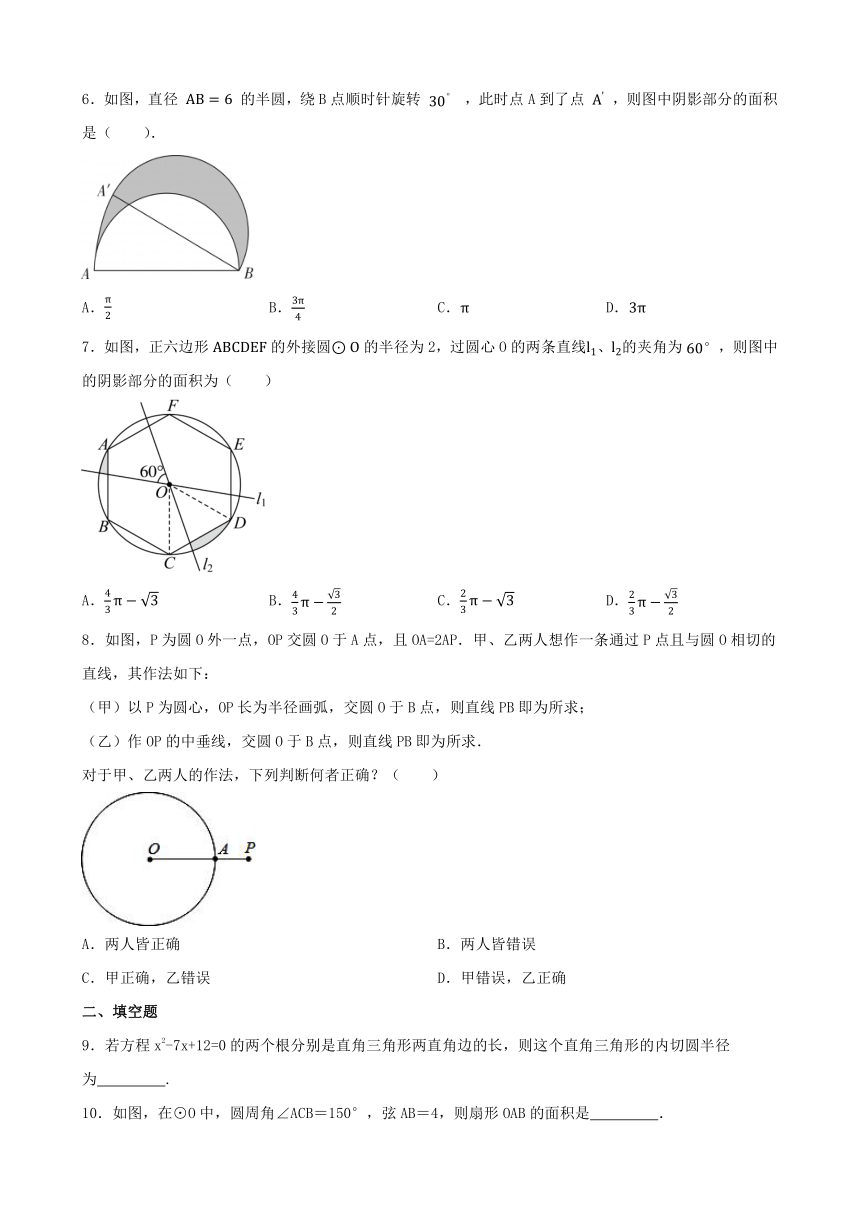
3.如图,△ABC中,∠A=90°,BC=2cm,分别以点B、C为圆心的两个等圆相外切,求两个图中两个阴影扇形的面积之和( )
A.4π B. C.π D.2π
4.如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE= ,CE=1.则 的长是( )
A. B. C. D.
5.如图,CD是圆O的直径,AB是圆O的弦,且CD=10,AB=8,若 于点E,则OE的长为( )
A.3 B.4 C.5 D.6
6.如图,直径 的半圆,绕B点顺时针旋转 ,此时点A到了点 ,则图中阴影部分的面积是( ).
A. B. C. D.
7.如图,正六边形的外接圆的半径为2,过圆心O的两条直线、的夹角为,则图中的阴影部分的面积为( )
A. B. C. D.
8.如图,P为圆O外一点,OP交圆O于A点,且OA=2AP.甲、乙两人想作一条通过P点且与圆O相切的直线,其作法如下:
(甲)以P为圆心,OP长为半径画弧,交圆O于B点,则直线PB即为所求;
(乙)作OP的中垂线,交圆O于B点,则直线PB即为所求.
对于甲、乙两人的作法,下列判断何者正确?( )
A.两人皆正确 B.两人皆错误
C.甲正确,乙错误 D.甲错误,乙正确
二、填空题
9.若方程x2-7x+12=0的两个根分别是直角三角形两直角边的长,则这个直角三角形的内切圆半径为 .
10.如图,在⊙O中,圆周角∠ACB=150°,弦AB=4,则扇形OAB的面积是 .
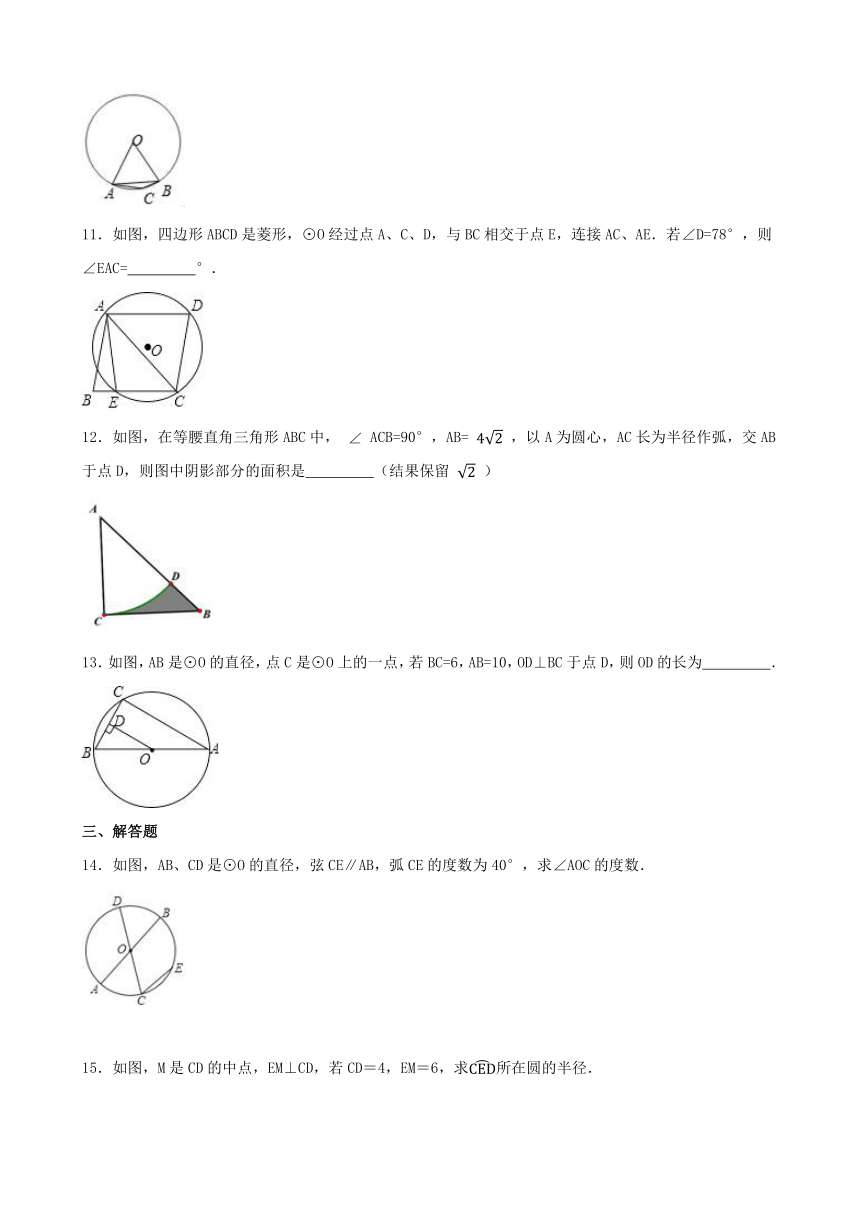
11.如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=78°,则∠EAC= °.
12.如图,在等腰直角三角形ABC中, ACB=90°,AB= ,以A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分的面积是 (结果保留 )
13.如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为 .
三、解答题
14.如图,AB、CD是⊙O的直径,弦CE∥AB,弧CE的度数为40°,求∠AOC的度数.
15.如图,M是CD的中点,EM⊥CD,若CD=4,EM=6,求所在圆的半径.
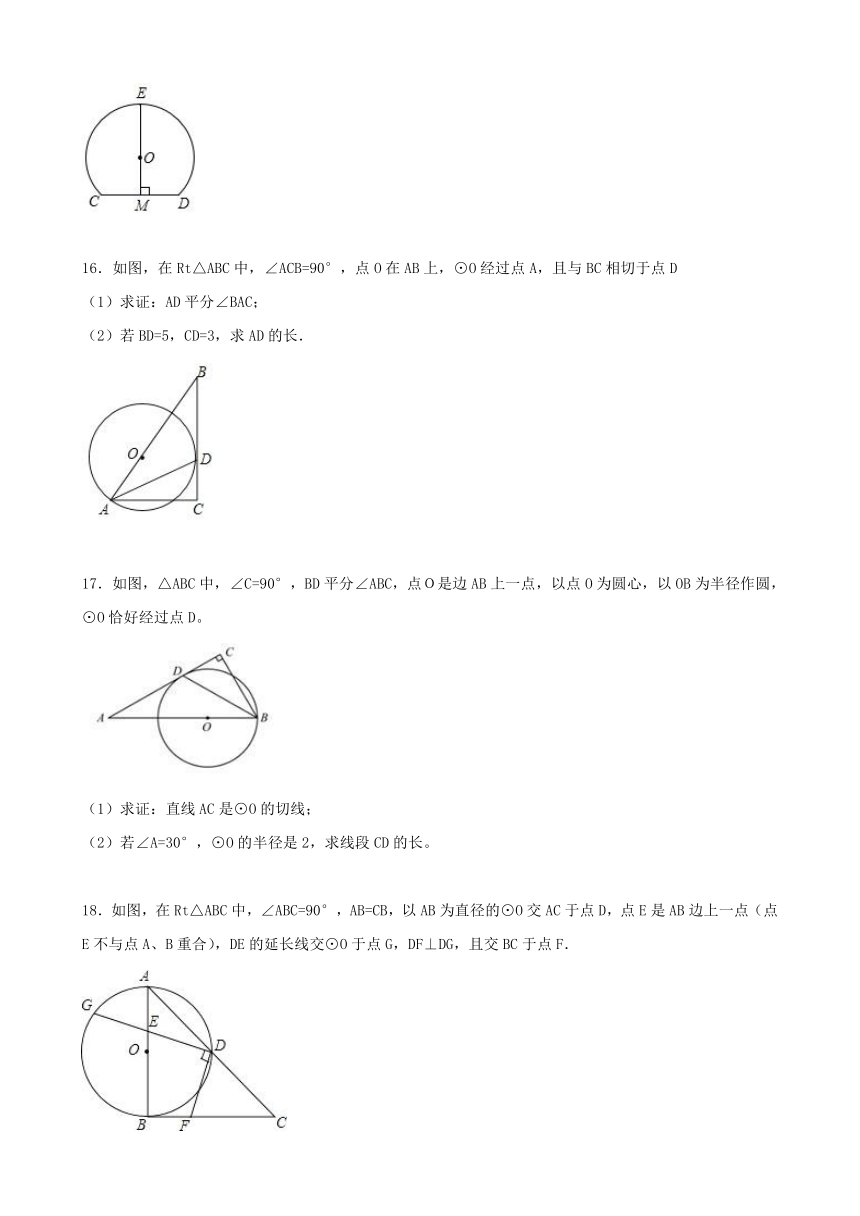
16.如图,在Rt△ABC中,∠ACB=90°,点O在AB上,⊙O经过点A,且与BC相切于点D
(1)求证:AD平分∠BAC;
(2)若BD=5,CD=3,求AD的长.
17.如图,△ABC中,∠C=90°,BD平分∠ABC,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好经过点D。
(1)求证:直线AC是⊙O的切线;
(2)若∠A=30°,⊙O的半径是2,求线段CD的长。
18.如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
答案
1.D
2.A
3.B
4.B
5.A
6.D
7.C
8.B
9.1
10.
11.27
12.
13.4
14.解:连接OE,如图,
∵弧CE的度数为40°,
∴∠COE=40°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣40°)÷2=70°,
∵弦CE∥AB,
∴∠AOC=∠OCE=70°.
15.解:连接OC,
∵M是CD的中点,EM⊥CD,
∴EM过⊙O的圆心点O, CM=CD=2 ,
设半径为x,
∵EM=6,
∴OM=EM-OE=6-x,
在Rt△OCM中,OM2+CM2=OC2, 即(6-x)2+22=x2,
解得:x=.
∴所在圆的半径为.
16.(1)证明:如图,连接OD,
∵BC为圆O的切线,
∴OD⊥CB,
∵AC⊥CB,
∴OD∥AC,
∴∠CAD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠CAD=∠OAD,
∴AD平分∠BAC;
(2)解:作ED⊥AB于E,
∵AD平分∠BAC,
∴DE=DC=3,
在Rt△BDE中,BD=5,DE=3,
根据勾股定理得:BE=4,
∵∠ABC=∠DBE,∠C=∠BED=90°,
∴△ABC∽△DBE,
∴=,即=,
∴AB=10,
∴AE=AB﹣BE=10﹣4=6,
在Rt△ADE中,AD===3.
17.(1)证明:连接OD。
∵BD平分∠ABC,
∴∠DBC=∠DBA,
∵OD=OB,
∴∠ODB=∠DBA,
∴∠ODB=∠DBC
∴OD∥BC,
∴∠ODA=∠C=90°,
∴直线AC是⊙O的切线;
(2)在Rt△ADO中,∠A=30°
∴AO=2DO=4,
∴AB=4+2=6,
∴BC=3,
在Rt△BCD中,
∠ABC=90°-30°=60°
∴∠DBC=∠DBA=30°,
设DC=x,则DB=2x,
∵DC2+BC2=BD ,
∴x2+9=4x2,解之得,x=
∴CD=
18.(1)证明:连接BD,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠A=∠C=45°,
∵AB为圆O的直径,
∴∠ADB=90°,即BD⊥AC,
∴AD=DC=BD= AC,∠CBD=∠C=45°,
∴∠A=∠FBD,
∵DF⊥DG,
∴∠FDG=90°,
∴∠FDB+∠BDG=90°,
∵∠EDA+∠BDG=90°,
∴∠EDA=∠FDB,
在△AED和△BFD中,
,
∴△AED≌△BFD(ASA),
∴AE=BF
(2)证明:连接EF,BG,
∵△AED≌△BFD,
∴DE=DF,
∵∠EDF=90°,
∴△EDF是等腰直角三角形,
∴∠DEF=45°,
∵∠G=∠A=45°,
∴∠G=∠DEF,
∴GB∥EF;
(3)∵AE=BF,AE=1,
∴BF=1,
在Rt△EBF中,∠EBF=90°,
∴根据勾股定理得:EF2=EB2+BF2,
∵EB=2,BF=1,
∴EF= = ,
∵△DEF为等腰直角三角形,∠EDF=90°,
∴cos∠DEF= ,
∵EF= ,
∴DE= × = ,
∵∠G=∠A,∠GEB=∠AED,
∴△GEB∽△AED,
∴ ,即GE ED=AE EB,
∴ GE=2,即GE= ,
则GD=GE+ED=
一、单选题
1.一条弦分圆周为5:7,这条弦所对的圆周角为( )
A.75° B.105° C.60°或120° D.75°或105°
2.如图,AB是⊙O的直径, = = ,∠COD=34°,则∠AEO的度数是( )
A.51° B.56° C.68° D.78°
3.如图,△ABC中,∠A=90°,BC=2cm,分别以点B、C为圆心的两个等圆相外切,求两个图中两个阴影扇形的面积之和( )
A.4π B. C.π D.2π
4.如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE= ,CE=1.则 的长是( )
A. B. C. D.
5.如图,CD是圆O的直径,AB是圆O的弦,且CD=10,AB=8,若 于点E,则OE的长为( )
A.3 B.4 C.5 D.6
6.如图,直径 的半圆,绕B点顺时针旋转 ,此时点A到了点 ,则图中阴影部分的面积是( ).
A. B. C. D.
7.如图,正六边形的外接圆的半径为2,过圆心O的两条直线、的夹角为,则图中的阴影部分的面积为( )
A. B. C. D.
8.如图,P为圆O外一点,OP交圆O于A点,且OA=2AP.甲、乙两人想作一条通过P点且与圆O相切的直线,其作法如下:
(甲)以P为圆心,OP长为半径画弧,交圆O于B点,则直线PB即为所求;
(乙)作OP的中垂线,交圆O于B点,则直线PB即为所求.
对于甲、乙两人的作法,下列判断何者正确?( )
A.两人皆正确 B.两人皆错误
C.甲正确,乙错误 D.甲错误,乙正确
二、填空题
9.若方程x2-7x+12=0的两个根分别是直角三角形两直角边的长,则这个直角三角形的内切圆半径为 .
10.如图,在⊙O中,圆周角∠ACB=150°,弦AB=4,则扇形OAB的面积是 .
11.如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=78°,则∠EAC= °.
12.如图,在等腰直角三角形ABC中, ACB=90°,AB= ,以A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分的面积是 (结果保留 )
13.如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为 .
三、解答题
14.如图,AB、CD是⊙O的直径,弦CE∥AB,弧CE的度数为40°,求∠AOC的度数.
15.如图,M是CD的中点,EM⊥CD,若CD=4,EM=6,求所在圆的半径.
16.如图,在Rt△ABC中,∠ACB=90°,点O在AB上,⊙O经过点A,且与BC相切于点D
(1)求证:AD平分∠BAC;
(2)若BD=5,CD=3,求AD的长.
17.如图,△ABC中,∠C=90°,BD平分∠ABC,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好经过点D。
(1)求证:直线AC是⊙O的切线;
(2)若∠A=30°,⊙O的半径是2,求线段CD的长。
18.如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
答案
1.D
2.A
3.B
4.B
5.A
6.D
7.C
8.B
9.1
10.
11.27
12.
13.4
14.解:连接OE,如图,
∵弧CE的度数为40°,
∴∠COE=40°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣40°)÷2=70°,
∵弦CE∥AB,
∴∠AOC=∠OCE=70°.
15.解:连接OC,
∵M是CD的中点,EM⊥CD,
∴EM过⊙O的圆心点O, CM=CD=2 ,
设半径为x,
∵EM=6,
∴OM=EM-OE=6-x,
在Rt△OCM中,OM2+CM2=OC2, 即(6-x)2+22=x2,
解得:x=.
∴所在圆的半径为.
16.(1)证明:如图,连接OD,
∵BC为圆O的切线,
∴OD⊥CB,
∵AC⊥CB,
∴OD∥AC,
∴∠CAD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠CAD=∠OAD,
∴AD平分∠BAC;
(2)解:作ED⊥AB于E,
∵AD平分∠BAC,
∴DE=DC=3,
在Rt△BDE中,BD=5,DE=3,
根据勾股定理得:BE=4,
∵∠ABC=∠DBE,∠C=∠BED=90°,
∴△ABC∽△DBE,
∴=,即=,
∴AB=10,
∴AE=AB﹣BE=10﹣4=6,
在Rt△ADE中,AD===3.
17.(1)证明:连接OD。
∵BD平分∠ABC,
∴∠DBC=∠DBA,
∵OD=OB,
∴∠ODB=∠DBA,
∴∠ODB=∠DBC
∴OD∥BC,
∴∠ODA=∠C=90°,
∴直线AC是⊙O的切线;
(2)在Rt△ADO中,∠A=30°
∴AO=2DO=4,
∴AB=4+2=6,
∴BC=3,
在Rt△BCD中,
∠ABC=90°-30°=60°
∴∠DBC=∠DBA=30°,
设DC=x,则DB=2x,
∵DC2+BC2=BD ,
∴x2+9=4x2,解之得,x=
∴CD=
18.(1)证明:连接BD,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠A=∠C=45°,
∵AB为圆O的直径,
∴∠ADB=90°,即BD⊥AC,
∴AD=DC=BD= AC,∠CBD=∠C=45°,
∴∠A=∠FBD,
∵DF⊥DG,
∴∠FDG=90°,
∴∠FDB+∠BDG=90°,
∵∠EDA+∠BDG=90°,
∴∠EDA=∠FDB,
在△AED和△BFD中,
,
∴△AED≌△BFD(ASA),
∴AE=BF
(2)证明:连接EF,BG,
∵△AED≌△BFD,
∴DE=DF,
∵∠EDF=90°,
∴△EDF是等腰直角三角形,
∴∠DEF=45°,
∵∠G=∠A=45°,
∴∠G=∠DEF,
∴GB∥EF;
(3)∵AE=BF,AE=1,
∴BF=1,
在Rt△EBF中,∠EBF=90°,
∴根据勾股定理得:EF2=EB2+BF2,
∵EB=2,BF=1,
∴EF= = ,
∵△DEF为等腰直角三角形,∠EDF=90°,
∴cos∠DEF= ,
∵EF= ,
∴DE= × = ,
∵∠G=∠A,∠GEB=∠AED,
∴△GEB∽△AED,
∴ ,即GE ED=AE EB,
∴ GE=2,即GE= ,
则GD=GE+ED=
同课章节目录
