2024年中考数学一轮复习综合练习题:相似三角形(含解析)
文档属性
| 名称 | 2024年中考数学一轮复习综合练习题:相似三角形(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 527.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 00:00:00 | ||
图片预览



文档简介
2024年中考数学一轮复习综合练习题:相似三角形
一、单选题
1.已知 ,那么下列等式一定成立的是( )
A.x=2,y=3 B. C. D.
2.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D、E、F,AC与DF相交于点H,且AH=2,HB=1,BC=5,则 =( )
A. B.2 C. D.
3.如图, ∥ ∥ ,直线 , 与 ∥ ∥ 分别交于点A、B、C和点D、E、F,若AB∶BC=2∶3,EF=6,则DF的长是( )
A.8 B.9 C.4 D.10
4.下列所给条件中,不能使△ABC与△A’B’C’相似的是( )
A.AB=AC, A'B'=A'C',∠A=∠A'
B.∠A=40°,∠B=80°,∠A'=40°,∠C'=60°
C.,∠B=∠B'
D.,∠A=∠A'
5.已知△ABC∽△DEF,面积比为9:4,则△ABC与△DEF的对应边之比为( )
A.3:4 B.2:3 C.9:16 D.3:2
6.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③AE⊥EF;④△ADF∽△ECF,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
7.下列命题中:①任意两个等腰三角形都相似;②任意两个等边三角形都相似;③任意两个直角三角形都相似;④任意两个等腰直角三角形都相似;正确的是( )
A.①③ B.①④ C.②④ D.③④
8.如图,在中,点、分别在边、上,,已知,,则的长是( )
A. B. C. D.
9.如图,△ABC∽△A′B′C′,AD 和 A′D′分别是△ABC 和△A′B′C′的高,若 AD=2,A′D′=3,则△ABC 与△A′B′C′的面积的比为( )
A.4:9 B.9:4 C.2:3 D.3:2
10.如图,点O为正方形ABCD对角线BD的中点,BE平分∠DBC交DC于点E,延长BC到点F,使 ,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下五个结论中① ;② ;③ ;④ ,正确结论有( )
A.1 B.2 C.3 D.4
二、填空题
11.如图中两三角形相似,则x= .
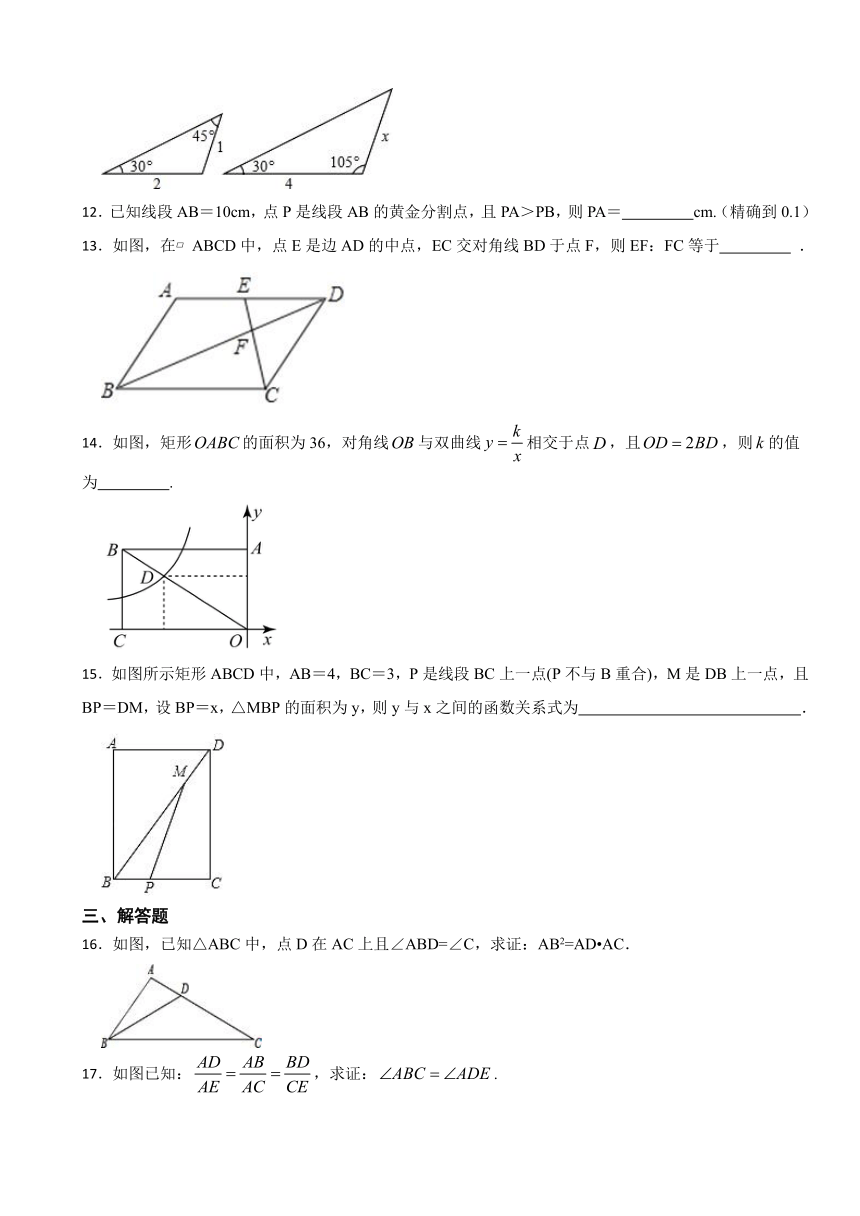
12.已知线段AB=10cm,点P是线段AB的黄金分割点,且PA>PB,则PA= cm.(精确到0.1)
13.如图,在 ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于 .
14.如图,矩形的面积为36,对角线与双曲线相交于点,且,则的值为 .
15.如图所示矩形ABCD中,AB=4,BC=3,P是线段BC上一点(P不与B重合),M是DB上一点,且BP=DM,设BP=x,△MBP的面积为y,则y与x之间的函数关系式为 .
三、解答题
16.如图,已知△ABC中,点D在AC上且∠ABD=∠C,求证:AB2=AD AC.
17.如图已知:,求证:.
18.如图,中有内接正方形DEFG,DE在BC边上,顶点G、F分别在AB、AC边上,,垂足为H,交GF于I.求证:.
19.如图1,在矩形ABCD中,AC与BD交于点O,E为AD上一点,CE与BD交于点F.
(1)若AE=CE,BD⊥CE,①求∠DEC的度数.②如图2,连接AF,当BC=3时,求AF的值.
(2)设(0<k<1),记△CBF的面积为S1,四边形ABFE的面积为S2,求的最大值.
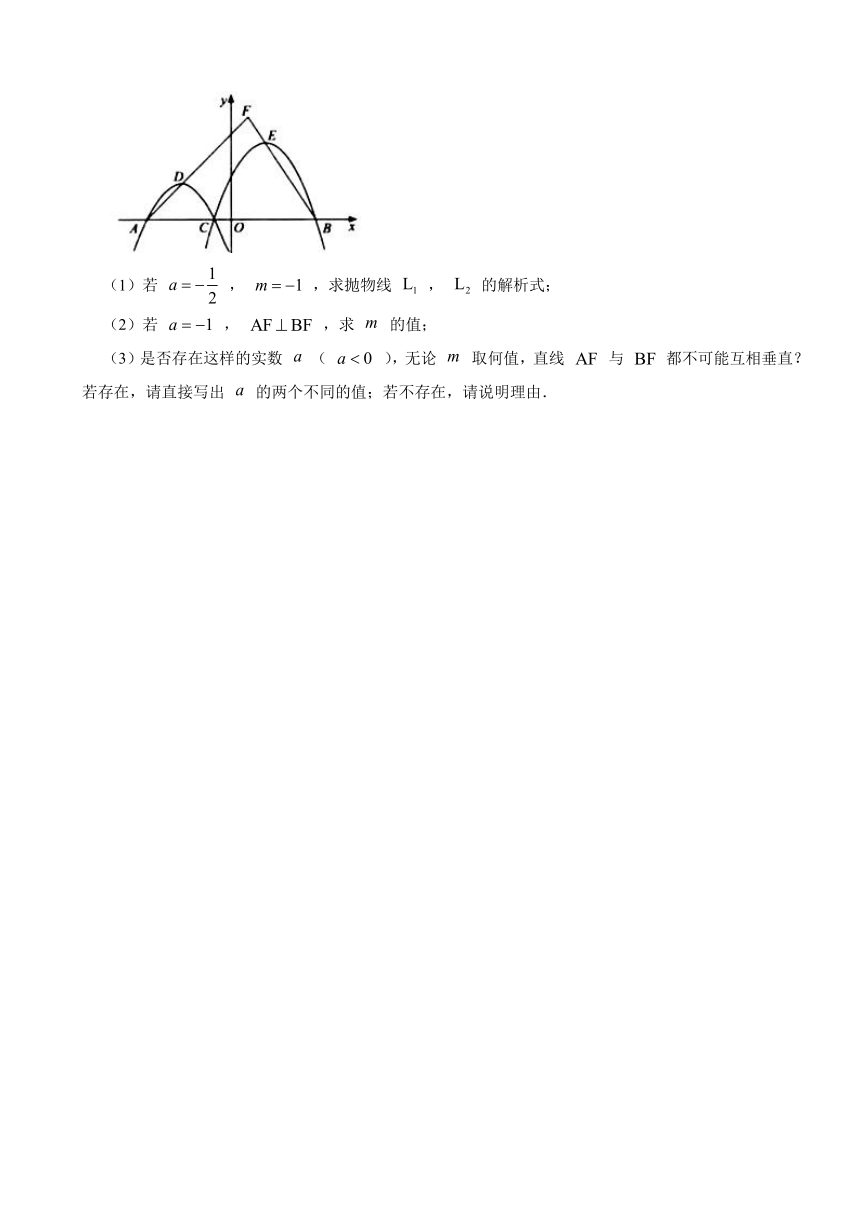
20.如图,在平面直角坐标系 中,已知 , 两点的坐标分别为 , , 是线段 上一点(与 , 点不重合),抛物线 ( )经过点 , ,顶点为 ,抛物线 ( )经过点 , ,顶点为 , , 的延长线相交于点 .
(1)若 , ,求抛物线 , 的解析式;
(2)若 , ,求 的值;
(3)是否存在这样的实数 ( ),无论 取何值,直线 与 都不可能互相垂直?若存在,请直接写出 的两个不同的值;若不存在,请说明理由.
答案解析部分
1.【答案】A
【解析】【解答】A,x=2,y=3时, ,符合题意;
B, 可得3y=2x,不符合题意;
C,当y=0时, 无意义,不符合题意;
D, 可得3x=-2y,不符合题意.
故答案为:A.
【分析】(1)当x=2,y=3时,计算可得左右两边都等于6,所以x=2,y=3时,等式3x=2y一定成立;
(2)将乘积式化为比例式得,;
(3)将乘积式化为比例式得,,但当y=0时,分式无意义;
(4)将等式移项得:3x-2y=0.
2.【答案】A
【解析】【解答】解:∵AH=2,HB=1,
∴AB=AH+BH=3,
∵l1∥l2∥l3,
∴ = = .
故答案为:A.
【分析】根据平行线分线段成比例定理“两条直线被一组平行线所截,截得的对应线段的长度成比例”可列比例式求解.
3.【答案】D
【解析】【解答】解:∵l1∥l2∥l3,
∴ ,
又∵ ,EF=6,
∴ ,
解得:DE=4,
∴DF=DE+EF=10.
故答案为:D.
【分析】根据“平行线分线段成比例定理”列出比例式,结合已知条件进行解答即可.
4.【答案】D
【解析】【分析】根据相似三角形的判定定理即可作出判断.
【解答】A、根据两个角对应相等的两个三角形相似可以判断,选项错误;
B、根据两对应边的比相等,夹角相等的两个三角形相似即可判断,故选项错误;
C、根据两对应边的比相等,夹角相等的两个三角形相似即可判断,故选项错误;
D、根据根据两对应边的比相等,且一边的对角相等的两个三角形不一定相似即可判断,故选项正确.
故选D.
5.【答案】D
【解析】【解答】解:∵△ABC∽△DEF,面积比为9:4,
∴△ABC与△DEF的对应边之比3:2.
故答案为:D.
【分析】由相似三角形的性质:相似比等于其面积比的算术平方根,代入数值即可.
6.【答案】B
【解析】【解答】解:∵在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,
设CF=x,则CD=4x,
∴DF=3x,BE=EC=2x,
∴ AB:EC=BE:CF=2:1.
∵∠B=∠C=90°,
∴△ABE∽△ECF,
∴AB:EC=AE:EF,∠AEB=∠EFC.
∵BE=CE,
∴AB:AE=BE:EF,
∵∠FEC+∠EFC=90°,∠AEB=∠EFC,
∴∠AEB+∠FEC=90°,
∴∠AEF=∠B=90°,
∴△ABE∽△AEF,AE⊥EF,
∴②③正确.
故答案为:B.
【分析】设CF=x,得AB=BC=CD=4x,DF=3x,BE=EC=2x,BE=AB,AB:EC=BE:CF=2:1,得△ABE∽△ECF,得AB:EC=AE:EF,∠AEB=∠EFC,从而得∠AEB+∠FEC=90°,AB:AE=BE:EF,得出AE⊥EF,△ABE∽△AEF,即可得出②③正确.
7.【答案】C
【解析】【解答】解:①不符合题意,因为没有说明角或边相等的条件,故不一定相似;
②符合题意,因为等边三个角都相等,故两三角形相似;
③不符合题意,只知道一个直角相等,不符合相似三角形判定的条件,故不一定相似;
④符合题意,因为其三对角均相等,符合相似三角形的判定条件,故相似;
所以②④符合题意,
故答案为:C.
【分析】根据相似三角形的判定方法逐一判断即可.
8.【答案】A
【解析】【解答】解:∵,
∴,
∴
∵ ,
∴
∴
故答案为:A.
【分析】根据,得到,再根据已知条件得到:进而求出的长.
9.【答案】A
【解析】【解答】解:∵AD和A′D′分别是△ABC和△A′B′C′的高,若AD=2,A′D′=3,
∴其相似比为2:3,
∴△ABC与△A′B′C′的面积的比为4:9;
故答案为:A.
【分析】根据相似三角形的性质可直接得出结论.
10.【答案】B
【解析】【解答】解:∵四边形ABCD是正方形,
.
∵BE平分∠DBC,
,
.
在 和 中,
,
.
,
,
.
在 和 中,
,
,
∴点H是DF的中点,
∴ ,故①正确;
,
,故②错误;
,
.
,
,故③错误;
,
,
,
.
,
,
,
,故④正确;
综上所述,正确的有①,④,
故答案为:B.
【分析】根据正方形的性质得出BC=CD,利用SAS证明△BCE≌△DC,得出∠EBC=∠CDF,∠BEC=∠CFD=675° ,然后利用ASA证明△DBH≌△HBF,得出DH=HF,即H是DF的中点则可判断①;根据等腰三角形的性质和三角形内角和定理求出∠CHF的度数,即可判断②;通过 ,得出BF与BC之间的关系,结合三角形中位线的性质得出CF = 2GH,再等量代换即可判断③;根据等腰直角三角形的性质及角度之间的关系证明△BHF∽△FHE,最后利用相似三角形的性质列比例式即可判断④.
11.【答案】2
【解析】【解答】解:由图形可得 = ,
解得x=2.
故答案为:2.
【分析】相似三角形的对应边与对应角相等,求出x的值。
12.【答案】6.2
【解析】【解答】解:∵点P是线段AB的黄金分割点,且AP>PB,∴AP= AB≈6.18(cm).
故答案为:6.18.
【分析】根据黄金分割的定义得出,较长线段是较短线段与整个线段的比例中项列出方程,求解即可.
13.【答案】1:2
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△DEF∽△DCF,
∴,
∵点E是边AD的中点,
∴DE=AE=BC,
∴=.
故答案为:1:2.
【分析】利用平行四边形的性质得出AD∥BC,AD=BC,进而得出△DEF∽△DCF,再利用相似三角形的判定与性质得出答案.
14.【答案】-16
【解析】【解答】解:如图,连接,过点D作于E,
∵矩形的面积为36,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵双曲线图象过点D,
∴,
又∵双曲线图象在第二象限,
∴,
∴,
故答案为:-16.
【分析】连接CD,过点D作DE⊥CO于E,根据矩形的面积可得S△BCO=18,根据等高的三角形面积之比等于对应底边的比可求出△CDO的面积,证明△ODE∽△OBC,根据相似三角形的性质可求出△DEO的面积,然后结合反比例函数系数k的几何意义就可求出k的值.
15.【答案】y=﹣ x2+2x(0<x≤3)
【解析】【解答】解:过点M作ME⊥AD,垂足为点E,延长EM交BC于点F,如图所示.
∵四边形ABCD为矩形,
∴AD=BC=3,∠A=90°.
在Rt△ABD中,AB=4,AD=3,
∴BD= =5.
∵ME⊥AD,
∴∠DEM=∠A=90°.
又∵∠EDM=∠ADB,
∴△DEM∽△DAB,
∴
∴EM= = x,
∴MF=AB﹣EM=(4﹣ x),
∴y= BP MF=﹣ x2+2x.
故答案为:y=﹣ x2+2x(0<x≤3).
【分析】过点M作ME⊥AD,垂足为点E,延长EM交BC于点F,由矩形的性质可得出AD=BC=3,∠A=90°,在Rt△ABD中,利用勾股定理可求出BD的长,由ME⊥AD,可得出∠DEM=∠A=90°,结合∠EDM=∠ADB,可得出△DEM∽△DAB,利用相似三角形的性质可用含x的代数式表示出EM,进而可得出MF的长,再利用三角形的面积公式即可得出y关于x的函数关系式.
16.【答案】解∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,
∴ ,
∴AB2=AD AC.
【解析】【分析】首先判断出△ABD∽△ACB,然后根据相似三角形对应边成比例得出,然后将比例式改为等积式即可。
17.【答案】证明:∵,
∴△ABD∽△ACE,
∴∠BAD=∠CAE,
∴∠DAE=∠BAC,
∵,
∴△ABC∽△ADE,
∴∠ABC=∠ADE.
【解析】【分析】由,可证得△ABD∽△ACE,继而可得∠DAE=∠BAC,即可证得△ABC∽△ADE,继而证得结论.
18.【答案】证明:∵四边形DEFG是正方形
∴,
∴
∴
∴
∴
∵
∴
【解析】【分析】利用相似三角形的判定与性质证明求解即可。
19.【答案】(1)解:①,
即,
②过点F作于点,
在Rt中,,
,
在Rt中,,
,
,
在Rt中,,
,
,
,
;
(2)设,
,
,
,
,
∵
∴
∵
∴∠FHD=90°
∴∠FHD=∠BAD,
又∵∠FDH=∠BDA,
∴
∴
∴
∴
∴
∴
当时,的最大值为.
【解析】【分析】(1) ① 先利用等腰三角形的性质得到,再根据矩形的性质可得,,进而得到,然后通过计算得.
② 作,利用直角三角形、的性质得到,,进而得到,再通过直角三角形的性质得到FH、DH的长度,然后由勾股定理计算出AF的长度.
(2)设,根据相似三角形的性质可得,故,又由可得,再根据得,故,从而得,因此,故当时,的最大值为.
20.【答案】(1)解:依题可得:
解得 :
所以抛物线L1的解析式为y=-x2-x-2.
同理,
解得 :
所以抛物线L2的解析式为y= -x2+x+2.
(2)解:如图,过点D作DG⊥x轴于点G,过点E作EH⊥x轴于点H.依题可得:解得∴抛物线L1的解析式为y=-x2+(m-4)x+4m.∴点D的坐标为(-,).∴DG==,AG=.同理可得,抛物线L2的解析式为y=-x2+(m+4)x-4mEH== ,BH=.∵AF⊥BF,DG⊥x轴,EH⊥x轴∴∠AFB=∠AGD=∠EHB=90°∴∠ADG=∠ABF=90°-∠BAF∴△ADG∽△EBH∴=.∴=∴m=2或m=-2.
(3)解:存在,例如a=-,a=-.
【解析】【分析】(1)把a、m代入得到已知点,把点代入函数解析式构成方程组,根据待定系数法可求出函数解析式.
(2)如图,过点D作DG⊥x轴于点G,过点E作EH⊥x轴于点H,把a=-1代入函数解析式,然后结合(m,0)和(-4,0)代入可解出函数解析式L1,然后分别求出D点坐标,得到DG,AG的长,同理得到L2;求得EH,BH的长,再根据三角形相似的判定与性质构造方程求解即可.
(3)根据前面的解答,直接写出即可.
一、单选题
1.已知 ,那么下列等式一定成立的是( )
A.x=2,y=3 B. C. D.
2.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D、E、F,AC与DF相交于点H,且AH=2,HB=1,BC=5,则 =( )
A. B.2 C. D.
3.如图, ∥ ∥ ,直线 , 与 ∥ ∥ 分别交于点A、B、C和点D、E、F,若AB∶BC=2∶3,EF=6,则DF的长是( )
A.8 B.9 C.4 D.10
4.下列所给条件中,不能使△ABC与△A’B’C’相似的是( )
A.AB=AC, A'B'=A'C',∠A=∠A'
B.∠A=40°,∠B=80°,∠A'=40°,∠C'=60°
C.,∠B=∠B'
D.,∠A=∠A'
5.已知△ABC∽△DEF,面积比为9:4,则△ABC与△DEF的对应边之比为( )
A.3:4 B.2:3 C.9:16 D.3:2
6.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③AE⊥EF;④△ADF∽△ECF,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
7.下列命题中:①任意两个等腰三角形都相似;②任意两个等边三角形都相似;③任意两个直角三角形都相似;④任意两个等腰直角三角形都相似;正确的是( )
A.①③ B.①④ C.②④ D.③④
8.如图,在中,点、分别在边、上,,已知,,则的长是( )
A. B. C. D.
9.如图,△ABC∽△A′B′C′,AD 和 A′D′分别是△ABC 和△A′B′C′的高,若 AD=2,A′D′=3,则△ABC 与△A′B′C′的面积的比为( )
A.4:9 B.9:4 C.2:3 D.3:2
10.如图,点O为正方形ABCD对角线BD的中点,BE平分∠DBC交DC于点E,延长BC到点F,使 ,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下五个结论中① ;② ;③ ;④ ,正确结论有( )
A.1 B.2 C.3 D.4
二、填空题
11.如图中两三角形相似,则x= .
12.已知线段AB=10cm,点P是线段AB的黄金分割点,且PA>PB,则PA= cm.(精确到0.1)
13.如图,在 ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于 .
14.如图,矩形的面积为36,对角线与双曲线相交于点,且,则的值为 .
15.如图所示矩形ABCD中,AB=4,BC=3,P是线段BC上一点(P不与B重合),M是DB上一点,且BP=DM,设BP=x,△MBP的面积为y,则y与x之间的函数关系式为 .
三、解答题
16.如图,已知△ABC中,点D在AC上且∠ABD=∠C,求证:AB2=AD AC.
17.如图已知:,求证:.
18.如图,中有内接正方形DEFG,DE在BC边上,顶点G、F分别在AB、AC边上,,垂足为H,交GF于I.求证:.
19.如图1,在矩形ABCD中,AC与BD交于点O,E为AD上一点,CE与BD交于点F.
(1)若AE=CE,BD⊥CE,①求∠DEC的度数.②如图2,连接AF,当BC=3时,求AF的值.
(2)设(0<k<1),记△CBF的面积为S1,四边形ABFE的面积为S2,求的最大值.
20.如图,在平面直角坐标系 中,已知 , 两点的坐标分别为 , , 是线段 上一点(与 , 点不重合),抛物线 ( )经过点 , ,顶点为 ,抛物线 ( )经过点 , ,顶点为 , , 的延长线相交于点 .
(1)若 , ,求抛物线 , 的解析式;
(2)若 , ,求 的值;
(3)是否存在这样的实数 ( ),无论 取何值,直线 与 都不可能互相垂直?若存在,请直接写出 的两个不同的值;若不存在,请说明理由.
答案解析部分
1.【答案】A
【解析】【解答】A,x=2,y=3时, ,符合题意;
B, 可得3y=2x,不符合题意;
C,当y=0时, 无意义,不符合题意;
D, 可得3x=-2y,不符合题意.
故答案为:A.
【分析】(1)当x=2,y=3时,计算可得左右两边都等于6,所以x=2,y=3时,等式3x=2y一定成立;
(2)将乘积式化为比例式得,;
(3)将乘积式化为比例式得,,但当y=0时,分式无意义;
(4)将等式移项得:3x-2y=0.
2.【答案】A
【解析】【解答】解:∵AH=2,HB=1,
∴AB=AH+BH=3,
∵l1∥l2∥l3,
∴ = = .
故答案为:A.
【分析】根据平行线分线段成比例定理“两条直线被一组平行线所截,截得的对应线段的长度成比例”可列比例式求解.
3.【答案】D
【解析】【解答】解:∵l1∥l2∥l3,
∴ ,
又∵ ,EF=6,
∴ ,
解得:DE=4,
∴DF=DE+EF=10.
故答案为:D.
【分析】根据“平行线分线段成比例定理”列出比例式,结合已知条件进行解答即可.
4.【答案】D
【解析】【分析】根据相似三角形的判定定理即可作出判断.
【解答】A、根据两个角对应相等的两个三角形相似可以判断,选项错误;
B、根据两对应边的比相等,夹角相等的两个三角形相似即可判断,故选项错误;
C、根据两对应边的比相等,夹角相等的两个三角形相似即可判断,故选项错误;
D、根据根据两对应边的比相等,且一边的对角相等的两个三角形不一定相似即可判断,故选项正确.
故选D.
5.【答案】D
【解析】【解答】解:∵△ABC∽△DEF,面积比为9:4,
∴△ABC与△DEF的对应边之比3:2.
故答案为:D.
【分析】由相似三角形的性质:相似比等于其面积比的算术平方根,代入数值即可.
6.【答案】B
【解析】【解答】解:∵在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,
设CF=x,则CD=4x,
∴DF=3x,BE=EC=2x,
∴ AB:EC=BE:CF=2:1.
∵∠B=∠C=90°,
∴△ABE∽△ECF,
∴AB:EC=AE:EF,∠AEB=∠EFC.
∵BE=CE,
∴AB:AE=BE:EF,
∵∠FEC+∠EFC=90°,∠AEB=∠EFC,
∴∠AEB+∠FEC=90°,
∴∠AEF=∠B=90°,
∴△ABE∽△AEF,AE⊥EF,
∴②③正确.
故答案为:B.
【分析】设CF=x,得AB=BC=CD=4x,DF=3x,BE=EC=2x,BE=AB,AB:EC=BE:CF=2:1,得△ABE∽△ECF,得AB:EC=AE:EF,∠AEB=∠EFC,从而得∠AEB+∠FEC=90°,AB:AE=BE:EF,得出AE⊥EF,△ABE∽△AEF,即可得出②③正确.
7.【答案】C
【解析】【解答】解:①不符合题意,因为没有说明角或边相等的条件,故不一定相似;
②符合题意,因为等边三个角都相等,故两三角形相似;
③不符合题意,只知道一个直角相等,不符合相似三角形判定的条件,故不一定相似;
④符合题意,因为其三对角均相等,符合相似三角形的判定条件,故相似;
所以②④符合题意,
故答案为:C.
【分析】根据相似三角形的判定方法逐一判断即可.
8.【答案】A
【解析】【解答】解:∵,
∴,
∴
∵ ,
∴
∴
故答案为:A.
【分析】根据,得到,再根据已知条件得到:进而求出的长.
9.【答案】A
【解析】【解答】解:∵AD和A′D′分别是△ABC和△A′B′C′的高,若AD=2,A′D′=3,
∴其相似比为2:3,
∴△ABC与△A′B′C′的面积的比为4:9;
故答案为:A.
【分析】根据相似三角形的性质可直接得出结论.
10.【答案】B
【解析】【解答】解:∵四边形ABCD是正方形,
.
∵BE平分∠DBC,
,
.
在 和 中,
,
.
,
,
.
在 和 中,
,
,
∴点H是DF的中点,
∴ ,故①正确;
,
,故②错误;
,
.
,
,故③错误;
,
,
,
.
,
,
,
,故④正确;
综上所述,正确的有①,④,
故答案为:B.
【分析】根据正方形的性质得出BC=CD,利用SAS证明△BCE≌△DC,得出∠EBC=∠CDF,∠BEC=∠CFD=675° ,然后利用ASA证明△DBH≌△HBF,得出DH=HF,即H是DF的中点则可判断①;根据等腰三角形的性质和三角形内角和定理求出∠CHF的度数,即可判断②;通过 ,得出BF与BC之间的关系,结合三角形中位线的性质得出CF = 2GH,再等量代换即可判断③;根据等腰直角三角形的性质及角度之间的关系证明△BHF∽△FHE,最后利用相似三角形的性质列比例式即可判断④.
11.【答案】2
【解析】【解答】解:由图形可得 = ,
解得x=2.
故答案为:2.
【分析】相似三角形的对应边与对应角相等,求出x的值。
12.【答案】6.2
【解析】【解答】解:∵点P是线段AB的黄金分割点,且AP>PB,∴AP= AB≈6.18(cm).
故答案为:6.18.
【分析】根据黄金分割的定义得出,较长线段是较短线段与整个线段的比例中项列出方程,求解即可.
13.【答案】1:2
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△DEF∽△DCF,
∴,
∵点E是边AD的中点,
∴DE=AE=BC,
∴=.
故答案为:1:2.
【分析】利用平行四边形的性质得出AD∥BC,AD=BC,进而得出△DEF∽△DCF,再利用相似三角形的判定与性质得出答案.
14.【答案】-16
【解析】【解答】解:如图,连接,过点D作于E,
∵矩形的面积为36,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵双曲线图象过点D,
∴,
又∵双曲线图象在第二象限,
∴,
∴,
故答案为:-16.
【分析】连接CD,过点D作DE⊥CO于E,根据矩形的面积可得S△BCO=18,根据等高的三角形面积之比等于对应底边的比可求出△CDO的面积,证明△ODE∽△OBC,根据相似三角形的性质可求出△DEO的面积,然后结合反比例函数系数k的几何意义就可求出k的值.
15.【答案】y=﹣ x2+2x(0<x≤3)
【解析】【解答】解:过点M作ME⊥AD,垂足为点E,延长EM交BC于点F,如图所示.
∵四边形ABCD为矩形,
∴AD=BC=3,∠A=90°.
在Rt△ABD中,AB=4,AD=3,
∴BD= =5.
∵ME⊥AD,
∴∠DEM=∠A=90°.
又∵∠EDM=∠ADB,
∴△DEM∽△DAB,
∴
∴EM= = x,
∴MF=AB﹣EM=(4﹣ x),
∴y= BP MF=﹣ x2+2x.
故答案为:y=﹣ x2+2x(0<x≤3).
【分析】过点M作ME⊥AD,垂足为点E,延长EM交BC于点F,由矩形的性质可得出AD=BC=3,∠A=90°,在Rt△ABD中,利用勾股定理可求出BD的长,由ME⊥AD,可得出∠DEM=∠A=90°,结合∠EDM=∠ADB,可得出△DEM∽△DAB,利用相似三角形的性质可用含x的代数式表示出EM,进而可得出MF的长,再利用三角形的面积公式即可得出y关于x的函数关系式.
16.【答案】解∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,
∴ ,
∴AB2=AD AC.
【解析】【分析】首先判断出△ABD∽△ACB,然后根据相似三角形对应边成比例得出,然后将比例式改为等积式即可。
17.【答案】证明:∵,
∴△ABD∽△ACE,
∴∠BAD=∠CAE,
∴∠DAE=∠BAC,
∵,
∴△ABC∽△ADE,
∴∠ABC=∠ADE.
【解析】【分析】由,可证得△ABD∽△ACE,继而可得∠DAE=∠BAC,即可证得△ABC∽△ADE,继而证得结论.
18.【答案】证明:∵四边形DEFG是正方形
∴,
∴
∴
∴
∴
∵
∴
【解析】【分析】利用相似三角形的判定与性质证明求解即可。
19.【答案】(1)解:①,
即,
②过点F作于点,
在Rt中,,
,
在Rt中,,
,
,
在Rt中,,
,
,
,
;
(2)设,
,
,
,
,
∵
∴
∵
∴∠FHD=90°
∴∠FHD=∠BAD,
又∵∠FDH=∠BDA,
∴
∴
∴
∴
∴
∴
当时,的最大值为.
【解析】【分析】(1) ① 先利用等腰三角形的性质得到,再根据矩形的性质可得,,进而得到,然后通过计算得.
② 作,利用直角三角形、的性质得到,,进而得到,再通过直角三角形的性质得到FH、DH的长度,然后由勾股定理计算出AF的长度.
(2)设,根据相似三角形的性质可得,故,又由可得,再根据得,故,从而得,因此,故当时,的最大值为.
20.【答案】(1)解:依题可得:
解得 :
所以抛物线L1的解析式为y=-x2-x-2.
同理,
解得 :
所以抛物线L2的解析式为y= -x2+x+2.
(2)解:如图,过点D作DG⊥x轴于点G,过点E作EH⊥x轴于点H.依题可得:解得∴抛物线L1的解析式为y=-x2+(m-4)x+4m.∴点D的坐标为(-,).∴DG==,AG=.同理可得,抛物线L2的解析式为y=-x2+(m+4)x-4mEH== ,BH=.∵AF⊥BF,DG⊥x轴,EH⊥x轴∴∠AFB=∠AGD=∠EHB=90°∴∠ADG=∠ABF=90°-∠BAF∴△ADG∽△EBH∴=.∴=∴m=2或m=-2.
(3)解:存在,例如a=-,a=-.
【解析】【分析】(1)把a、m代入得到已知点,把点代入函数解析式构成方程组,根据待定系数法可求出函数解析式.
(2)如图,过点D作DG⊥x轴于点G,过点E作EH⊥x轴于点H,把a=-1代入函数解析式,然后结合(m,0)和(-4,0)代入可解出函数解析式L1,然后分别求出D点坐标,得到DG,AG的长,同理得到L2;求得EH,BH的长,再根据三角形相似的判定与性质构造方程求解即可.
(3)根据前面的解答,直接写出即可.
同课章节目录
