2023年中考数学高频考点专题练习-一次函数与一元一次不等式的综合(含答案)
文档属性
| 名称 | 2023年中考数学高频考点专题练习-一次函数与一元一次不等式的综合(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 457.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 00:00:00 | ||
图片预览





文档简介
2023年中考数学高频考点专题练习-一次函数与一元一次不等式的综合
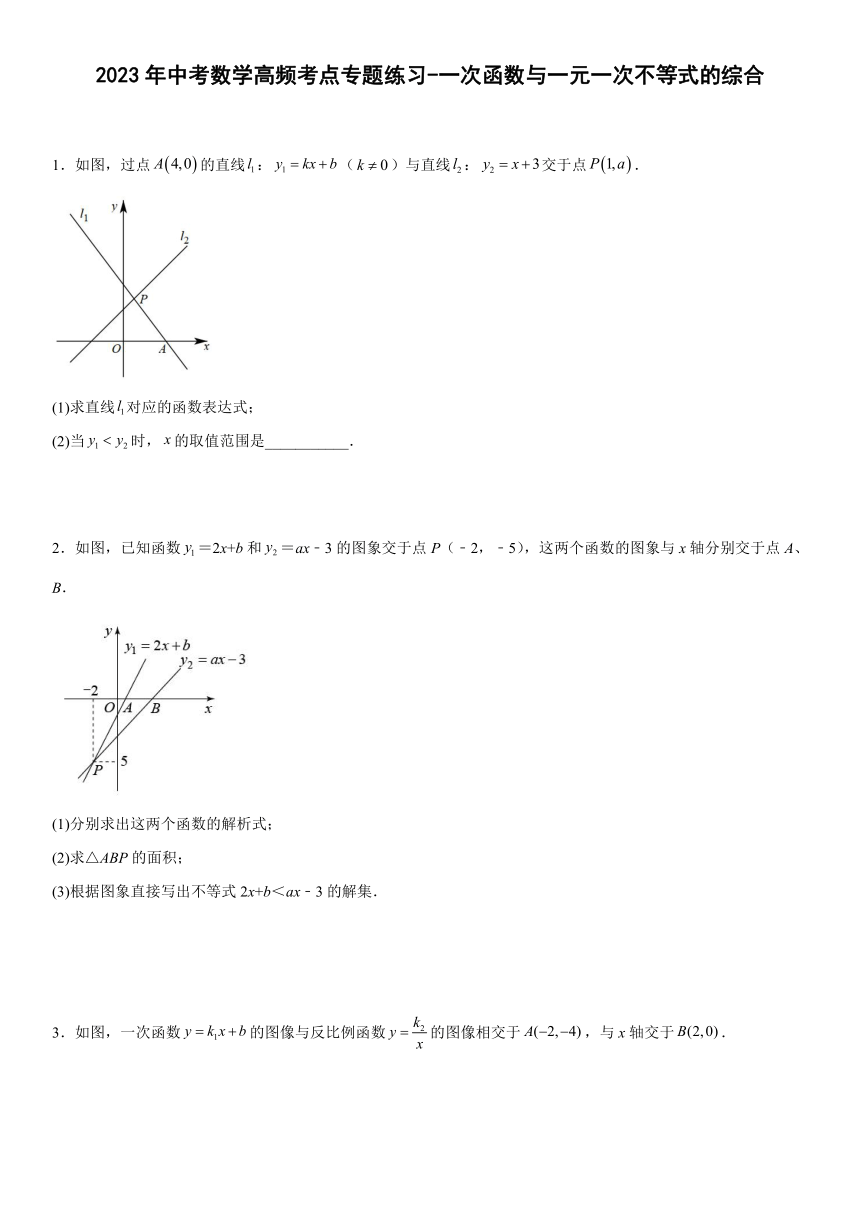
1.如图,过点的直线:()与直线:交于点.
(1)求直线对应的函数表达式;
(2)当时,的取值范围是___________.
2.如图,已知函数=2x+b和=ax﹣3的图象交于点P(﹣2,﹣5),这两个函数的图象与x轴分别交于点A、B.
(1)分别求出这两个函数的解析式;
(2)求△ABP的面积;
(3)根据图象直接写出不等式2x+b<ax﹣3的解集.
3.如图,一次函数的图像与反比例函数的图像相交于,与x轴交于.
(1)求反比例函数和一次函数的解析式,并在网格中画出反比例函数和一次函数的图像;
(2)连接,求的面积;
(3)根据图像,直接写出不等式的解集.
4.已知一次函数和反比例函数()的图像分别都过 两点.
(1)分别求出一次函数和反比例函数的解析式,并在给出的直角坐标系中直接画出一次函数和反比例函数的图像;
(2)已知点C是点B关于y轴的对称点,连接,求的面积:
(3)根据图像,直接写出满足的x的取值范围.
5.如图,直线y1=x+1交x轴、y轴于点A、B,直线y2=﹣2x+4交x、y轴于点C、D,两直线交于点E.
(1)求点E的坐标;
(2)求ACE的面积;
(3)根据图象直接回答:当x为何值时,y1<y2?
6.如图,在平面直角坐标系中,直线与x轴、y轴分别交于点A、B,点P也在直线上,已知点.
(1)求的长;
(2)若的面积与的面积相等,求点P的坐标;
(3)设直线与直线交点的横坐标为m,若,直接写出b的取值范围.
7.如图,在直角坐标系xOy中,直线经过点,直线与交于点,与y轴交于点B,点A关于x轴对称的点在直线上.
(1)求直线的函数表达式;
(2)连接AB,求的面积;
(3)过点作x轴的垂线,分别交,于点M,N,若M,N两点间的距离不小于5,直接写出n的取值范围.
8.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)请直接写出不等式kx+b﹣3x>0的解集;
(3)若点D在y=3x上,且满足S△BCD=2S△BOC,求点D的坐标.
9.如图,在平面直角坐标系中,点A,B的坐标分别为,,直线l的表达式为:.
(1)当时,直线l与x轴的交点的坐标是__________;
(2)嘉嘉发现:直线l恒过一点,请你通过计算找出这点;
(3)若线段AB与直线l有交点,请直接写出k的取值范围.
10.如图,函数和的图象相交于点.
(1)求m,a的值;
(2)根据图象,直接写出不等式的解集.
11.已知函数y=2x+m﹣3.
(1)若函数图象经过原点,求m的值.
(2)m为何值时,函数图象与y轴的交点在x轴的下方?
(3)若函数的图象平行直线y=(m﹣1)x﹣3,求m的值.
12.在数学学习中,及时对知识进行归纳和整理是完善知识结构的重要方法.善于学习的小明在学习了二元一次方程组、一元一次不等式和一次函数后,把相关知识归纳整理如下:
一次函数与方程的关系: (1)一次函数的解析式就是一个二元一次方程; (2)点的横坐标是方程①的解; (3)点的坐标中的,的值是方程组②的解. 一次函数与不等式的关系: (1)函数的函数值大于时,自变量的取值范围是不等式③的解集; (2)函数的函数值小于时,自变量的取值范围时不等式④的解集.
(1)请根据以上方框中的内容在下面数字序号后写出相应的结论:
①______;②______;③______;④______.
(2)若点,,的坐标分别为、、,则方程的解为______;
不等式的解集为______;
不等式的解集为______;
不等式组的解集为______.
13.如图,直线与x轴、y轴分别交于点A,B,直线经过点D(3,0),与直线交于点C(m,3).
(1)求直线CD的解析式;
(2)根据图象,直接写出关于x的不等式的解集;
(3)现有一点P在直线AB上,过点P作PQy轴交直线CD于点Q.若线段PQ的长为5,求点P的坐标.
14.如图所示,直线和直线相交于点A,点A的坐标为(1,n).
(1)求直线的解析式;
(2)当时,直接写出的取值范围.
15.如图,反比例函数(,)的图象与直线交于和,该函数关于x轴对称后的图象经过点.
(1)求和的解析式及m值;
(2)根据图象直接写出时x的取值范围;
(3)点M是x轴上一动点,求当取得最大值时M的坐标.
16.已知一次函数 y=-x+2.
(1)求这个函数的图像与两条坐标轴的交点坐标;
(2)在平面直角坐标系中画出这个函数的图像;
(3)结合函数图像回答问题:
①当 x>0 时,y 的取值范围是 ;
②当 y<0 时,x 的取值范围是 .
17.如图,在平面直角坐标系中,一次函数的图象与轴,轴分别交于,两点,与正比例函数的图象交于点,点的纵坐标为4.
(1)求,,三点的坐标;
(2)若动点在射线上运动,当的面积是的面积的时,求点的坐标;
(3)若点在的内部(不包括边界),请直接写出的取值范围.
参考答案:
1.(1)
(2)
2.(1),;
(2)
(3)
3.(1),,
(2)4
(3)或
4.(1),
(2)5
(3)或
5.(1)E(1,2)
(2)3
(3)
6.(1)
(2)点P的坐标为或
(3)
7.(1)
(2)
(3)或
8.(1),
(2)不等式kx+b﹣3x>0的解集为
(3)点D的坐标为:或
9.(1)
(2)
(3)
10.(1),
(2)>
11.(1)
(2)
(3)
12.(1);;;
(2);;;
13.(1)
(2)
(3)点P的坐标为(,7)或(,-1)
14.(1)
(2)
15.(1),,
(2)或
(3)
16.(1)这个函数的图像与坐标轴的交点为(0,2),(2,0);
(2)见解析
(3)①y<2;②x>2
17.(1)点的坐标是,点的坐标是点的坐标是
(2)点的坐标是,
(3)
1.如图,过点的直线:()与直线:交于点.
(1)求直线对应的函数表达式;
(2)当时,的取值范围是___________.
2.如图,已知函数=2x+b和=ax﹣3的图象交于点P(﹣2,﹣5),这两个函数的图象与x轴分别交于点A、B.
(1)分别求出这两个函数的解析式;
(2)求△ABP的面积;
(3)根据图象直接写出不等式2x+b<ax﹣3的解集.
3.如图,一次函数的图像与反比例函数的图像相交于,与x轴交于.
(1)求反比例函数和一次函数的解析式,并在网格中画出反比例函数和一次函数的图像;
(2)连接,求的面积;
(3)根据图像,直接写出不等式的解集.
4.已知一次函数和反比例函数()的图像分别都过 两点.
(1)分别求出一次函数和反比例函数的解析式,并在给出的直角坐标系中直接画出一次函数和反比例函数的图像;
(2)已知点C是点B关于y轴的对称点,连接,求的面积:
(3)根据图像,直接写出满足的x的取值范围.
5.如图,直线y1=x+1交x轴、y轴于点A、B,直线y2=﹣2x+4交x、y轴于点C、D,两直线交于点E.
(1)求点E的坐标;
(2)求ACE的面积;
(3)根据图象直接回答:当x为何值时,y1<y2?
6.如图,在平面直角坐标系中,直线与x轴、y轴分别交于点A、B,点P也在直线上,已知点.
(1)求的长;
(2)若的面积与的面积相等,求点P的坐标;
(3)设直线与直线交点的横坐标为m,若,直接写出b的取值范围.
7.如图,在直角坐标系xOy中,直线经过点,直线与交于点,与y轴交于点B,点A关于x轴对称的点在直线上.
(1)求直线的函数表达式;
(2)连接AB,求的面积;
(3)过点作x轴的垂线,分别交,于点M,N,若M,N两点间的距离不小于5,直接写出n的取值范围.
8.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)请直接写出不等式kx+b﹣3x>0的解集;
(3)若点D在y=3x上,且满足S△BCD=2S△BOC,求点D的坐标.
9.如图,在平面直角坐标系中,点A,B的坐标分别为,,直线l的表达式为:.
(1)当时,直线l与x轴的交点的坐标是__________;
(2)嘉嘉发现:直线l恒过一点,请你通过计算找出这点;
(3)若线段AB与直线l有交点,请直接写出k的取值范围.
10.如图,函数和的图象相交于点.
(1)求m,a的值;
(2)根据图象,直接写出不等式的解集.
11.已知函数y=2x+m﹣3.
(1)若函数图象经过原点,求m的值.
(2)m为何值时,函数图象与y轴的交点在x轴的下方?
(3)若函数的图象平行直线y=(m﹣1)x﹣3,求m的值.
12.在数学学习中,及时对知识进行归纳和整理是完善知识结构的重要方法.善于学习的小明在学习了二元一次方程组、一元一次不等式和一次函数后,把相关知识归纳整理如下:
一次函数与方程的关系: (1)一次函数的解析式就是一个二元一次方程; (2)点的横坐标是方程①的解; (3)点的坐标中的,的值是方程组②的解. 一次函数与不等式的关系: (1)函数的函数值大于时,自变量的取值范围是不等式③的解集; (2)函数的函数值小于时,自变量的取值范围时不等式④的解集.
(1)请根据以上方框中的内容在下面数字序号后写出相应的结论:
①______;②______;③______;④______.
(2)若点,,的坐标分别为、、,则方程的解为______;
不等式的解集为______;
不等式的解集为______;
不等式组的解集为______.
13.如图,直线与x轴、y轴分别交于点A,B,直线经过点D(3,0),与直线交于点C(m,3).
(1)求直线CD的解析式;
(2)根据图象,直接写出关于x的不等式的解集;
(3)现有一点P在直线AB上,过点P作PQy轴交直线CD于点Q.若线段PQ的长为5,求点P的坐标.
14.如图所示,直线和直线相交于点A,点A的坐标为(1,n).
(1)求直线的解析式;
(2)当时,直接写出的取值范围.
15.如图,反比例函数(,)的图象与直线交于和,该函数关于x轴对称后的图象经过点.
(1)求和的解析式及m值;
(2)根据图象直接写出时x的取值范围;
(3)点M是x轴上一动点,求当取得最大值时M的坐标.
16.已知一次函数 y=-x+2.
(1)求这个函数的图像与两条坐标轴的交点坐标;
(2)在平面直角坐标系中画出这个函数的图像;
(3)结合函数图像回答问题:
①当 x>0 时,y 的取值范围是 ;
②当 y<0 时,x 的取值范围是 .
17.如图,在平面直角坐标系中,一次函数的图象与轴,轴分别交于,两点,与正比例函数的图象交于点,点的纵坐标为4.
(1)求,,三点的坐标;
(2)若动点在射线上运动,当的面积是的面积的时,求点的坐标;
(3)若点在的内部(不包括边界),请直接写出的取值范围.
参考答案:
1.(1)
(2)
2.(1),;
(2)
(3)
3.(1),,
(2)4
(3)或
4.(1),
(2)5
(3)或
5.(1)E(1,2)
(2)3
(3)
6.(1)
(2)点P的坐标为或
(3)
7.(1)
(2)
(3)或
8.(1),
(2)不等式kx+b﹣3x>0的解集为
(3)点D的坐标为:或
9.(1)
(2)
(3)
10.(1),
(2)>
11.(1)
(2)
(3)
12.(1);;;
(2);;;
13.(1)
(2)
(3)点P的坐标为(,7)或(,-1)
14.(1)
(2)
15.(1),,
(2)或
(3)
16.(1)这个函数的图像与坐标轴的交点为(0,2),(2,0);
(2)见解析
(3)①y<2;②x>2
17.(1)点的坐标是,点的坐标是点的坐标是
(2)点的坐标是,
(3)
同课章节目录
