2023年浙江省中考·数学冲刺 思维课第4讲 开放型问题(无答案)
文档属性
| 名称 | 2023年浙江省中考·数学冲刺 思维课第4讲 开放型问题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 489.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 09:50:35 | ||
图片预览


文档简介
讲次 标题 课程内容 知识章节 等级 难度星级
中考冲刺第4讲 开放型问题 模块一:条件开放型 中考冲刺 4级 ★★★★☆
模块二:结论开放型
模块三:方法开放型
(1)如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是 .(只填一个即可)
(2)写出一个在三视图中俯视图与主视图完全相同的几何体 .
(3)如图,菱形ABCD中,对角线AC、BD相交于点O,不添加任何辅助线,请添加一个条件 ,使四边形ABCD是正方形(填一个即可).
【练习1】如图,AB,CD相交于点E,且AB=CD,试添加一个条件使得△ADE≌△CBE.现给出如下五个条件:①∠A=∠C;②∠B=∠D;③AE=CE;④BE=DE;⑤AD=CB.其中符合要求有( )
A. 2个 B. 3个 C. 4个 D. 5个
先化简:,再用一个你最喜欢的数代替计算结果.
【练习2】先化简,然后从的范围内选择一个合适的整数作为x的值代入求值.
已知一个函数,当时,函数值y随着x的增大而减小,请写出这个函数关系式__________.
【练习3】对于两个二次函数,,满足.当时,二次函数的函数值为5,且二次函数有最小值3.请写出两个符合题意的二次函数的解析式__________ (要求:写出的解析式的对称轴不能相同).
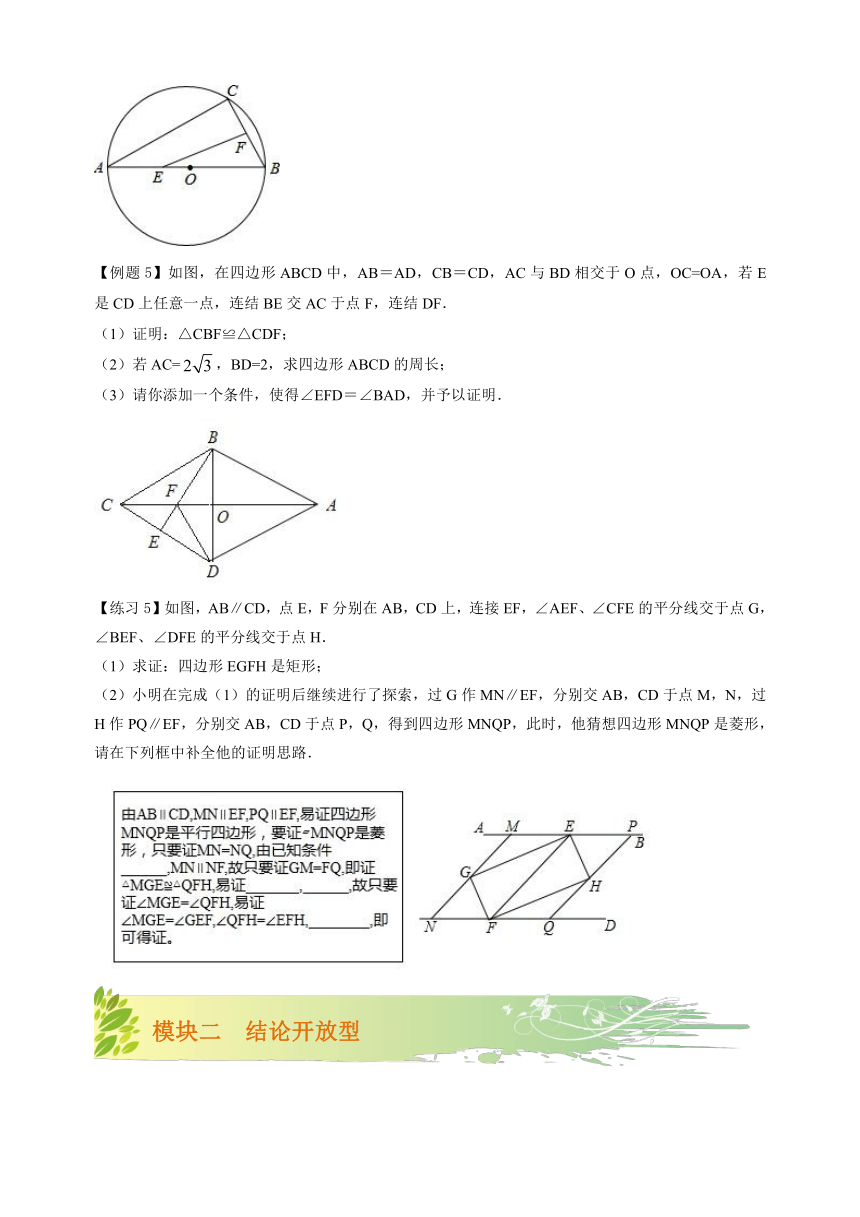
如图,AB是⊙O的弦,OC⊥AB于C,连接OA、OB,点P是半径OB上任意一点,连接AP.若OA=5cm,OC=3cm,则AP的长度可能是 6
cm(写出一个符合条件的数值即可)
【练习4】如图,AB是⊙O的直径,弦BC=4cm,F是弦BC的中点,∠ABC=60°.若动点E以1cm/s的速度从A点出发在AB上沿着A→B→A运动,设运动时间为t(s)(0≤t<16),连接EF,当t为______时,△BEF是直角三角形。4s
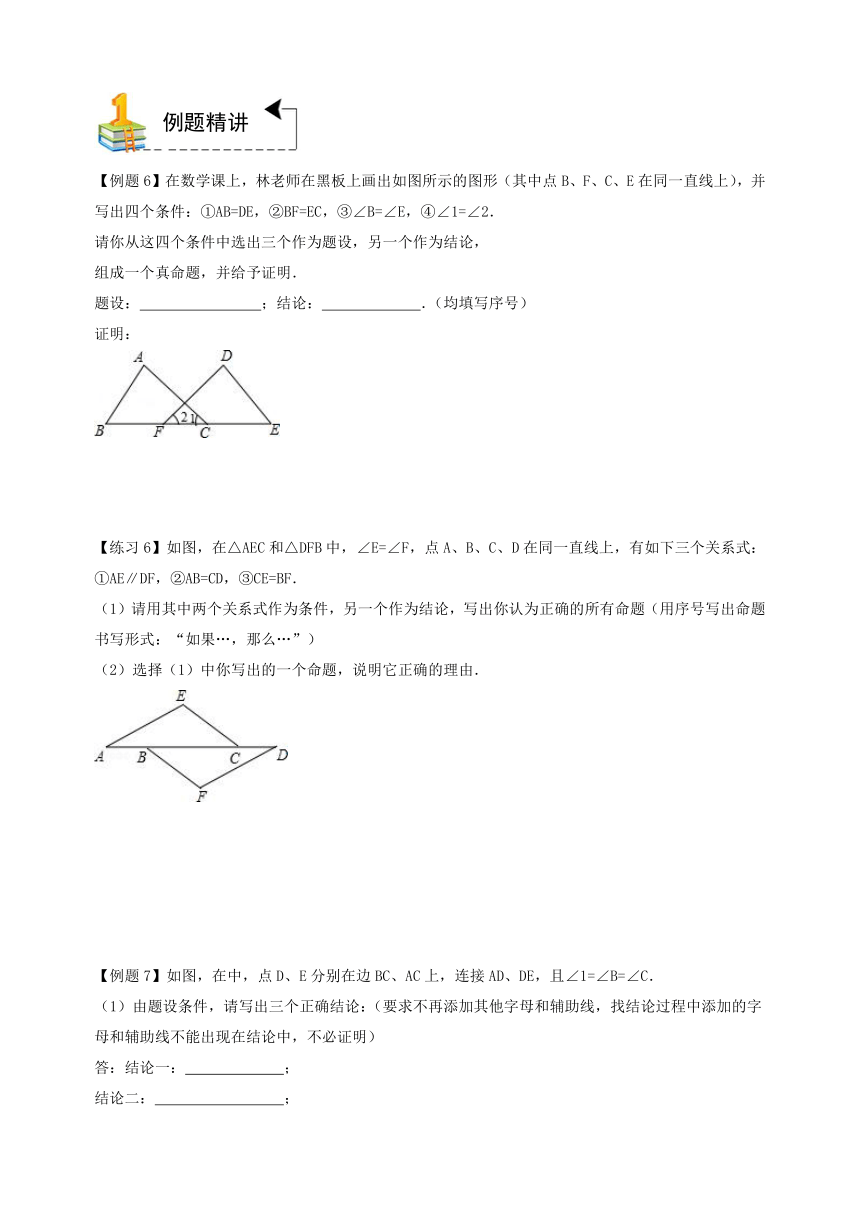
【例题5】如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连结BE交AC于点F,连结DF.
(1)证明:△CBF≌△CDF;
(2)若AC=,BD=2,求四边形ABCD的周长;
(3)请你添加一个条件,使得∠EFD=∠BAD,并予以证明.
【练习5】如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.
(1)求证:四边形EGFH是矩形;
(2)小明在完成(1)的证明后继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.
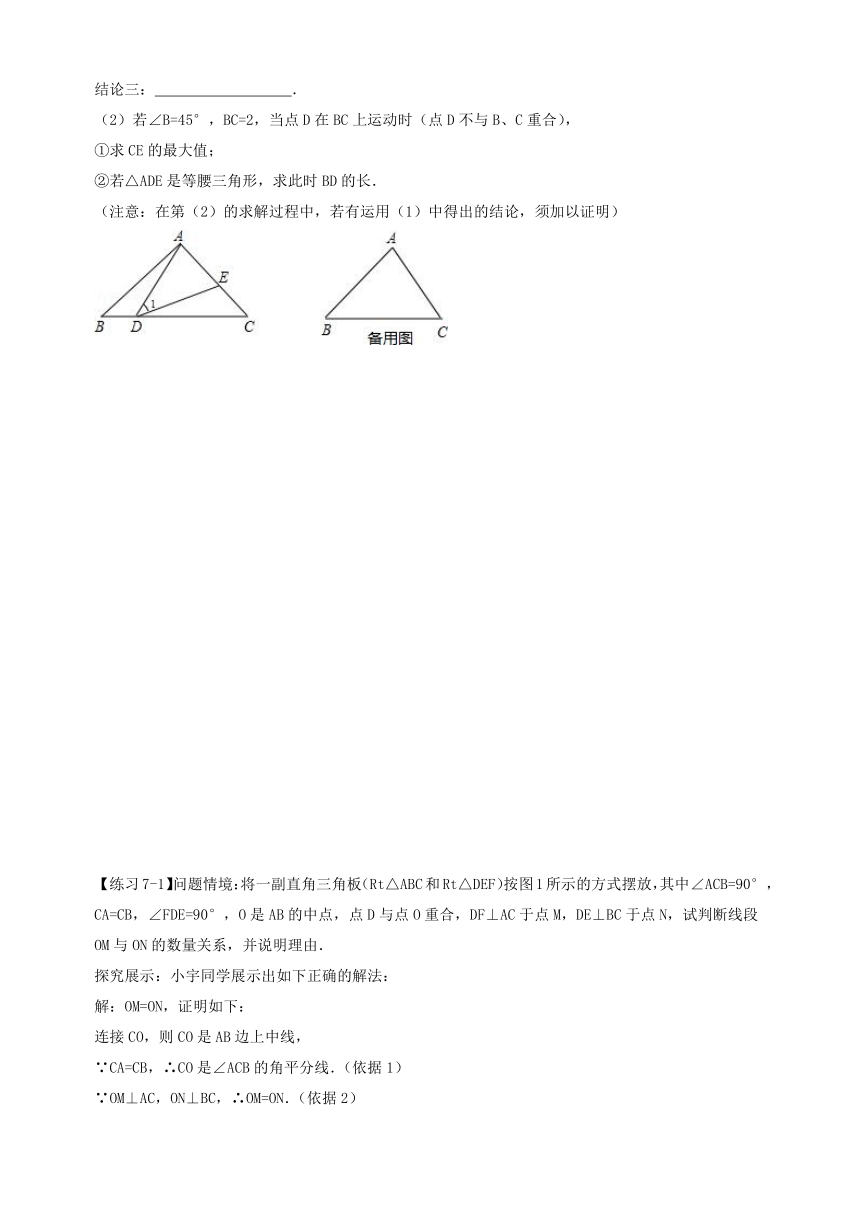
【例题6】在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.
请你从这四个条件中选出三个作为题设,另一个作为结论,
组成一个真命题,并给予证明.
题设: ;结论: .(均填写序号)
证明:
【练习6】如图,在△AEC和△DFB中,∠E=∠F,点A、B、C、D在同一直线上,有如下三个关系式:①AE∥DF,②AB=CD,③CE=BF.
(1)请用其中两个关系式作为条件,另一个作为结论,写出你认为正确的所有命题(用序号写出命题书写形式:“如果…,那么…”)
(2)选择(1)中你写出的一个命题,说明它正确的理由.
【例题7】如图,在中,点D、E分别在边BC、AC上,连接AD、DE,且∠1=∠B=∠C.
(1)由题设条件,请写出三个正确结论:(要求不再添加其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)
答:结论一: ;
结论二: ;
结论三: .
(2)若∠B=45°,BC=2,当点D在BC上运动时(点D不与B、C重合),
①求CE的最大值;
②若△ADE是等腰三角形,求此时BD的长.
(注意:在第(2)的求解过程中,若有运用(1)中得出的结论,须加以证明)
【练习7-1】问题情境:将一副直角三角板(Rt△ABC和Rt△DEF)按图1所示的方式摆放,其中∠ACB=90°,CA=CB,∠FDE=90°,O是AB的中点,点D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量关系,并说明理由.
探究展示:小宇同学展示出如下正确的解法:
解:OM=ON,证明如下:
连接CO,则CO是AB边上中线,
∵CA=CB,∴CO是∠ACB的角平分线.(依据1)
∵OM⊥AC,ON⊥BC,∴OM=ON.(依据2)
反思交流:
(1)上述证明过程中的“依据1”和“依据2”分别是指:
依据1:
依据2:
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
拓展延伸:
(3)将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置,使点D落在BA的延长线上,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连接OM、ON,试判断线段OM、ON的数量关系与位置关系,并写出证明过程.
【练习7-2】在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变,如图2、图3,线段BE、EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.
【例题8】阅读理解:我们把对非负实数 “四舍五入”到个位的值记为《》,即当为非负整数时,若,则《》=n.例如:《0.67》=1,《2.49》=2,….给出下列关于《》的问题:其中正确结论的个数是( )
①《》=2;
②《2》=2《》;
③当为非负整数时,《》=+《2》;
④若《》=5,则实数x的取值范围是;
⑤满足《》=的非负实数有三个.
A.1 B.2 C.3 D.4
【练习8-1】如图,已知AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,AE的延长线交BC于点F,连接AD、BD.给出以下结论:①AD∥OC;②FC=FE;③点E为的内心.其中正确的是________________(填序号)
【练习8-2】图AB是⊙O的直径,BC是⊙O弦OD⊥CB于点E,交于点D
(1)请写出三个不同类型的正确结论:
(2)连结CD,设,,求、的关系
解题思路及方法:
找特征(中点、特殊角、折叠等),找模型:相似(母子型、A字型、八字型)三线合一、面积等;
借助问与问之间的联系,寻找条件和思路。
照搬:照搬上一问的方法,思路解决问题,如照搬字母、辅助线、全等、相似等。
找结构:寻找不变的结构,利用不变结构的特征解决问题。
【例题9】阅读理解:
我们把满足某种条件的所有点所组成的图形,叫做符合这个条件的点的轨迹.
例如:角的平分线是到角的两边距离相等的点的轨迹.
问题:如图1,已知EF为△ABC的中位线,M是边BC上一动点,连接AM交EF于点P,那么动点P为线段AM中点.
理由:∵线段EF为△ABC的中位线,∴EF∥BC,
由平行线分线段成比例得:动点P为线段AM中点.
由此你得到动点P的运动轨迹是:______.
知识应用:如图2,已知EF为等边△ABC边AB、AC上的动点,连结EF;若AF=BE,且等边△ABC的边长为8,求线段EF中点Q的运动轨迹的长.
拓展提高:如图3,P为线段AB上一动点(点P不与点A、B重合),在线段AB的同侧分别作等边△APC和等边△PBD,连结AD、BC,交点为Q.
(1)求∠AQB的度数;
(2)若AB=6,求动点Q运动轨迹的长.
【例题10】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得:的值为常数,则= .
如图,若AC、BD、EF两两互相平分于点O,请写出图中的一对全等三角形(只需写一对即可)_________.
如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是______.(注:将你认为正确的结论都填上)
如图,已知AC=DB,要使△ABC≌△DCB,只需增加的一个条件是_________或_________.
如图,下面四个条件中,请你以其中两个为已知条件,第三个为结论,推出一个正确的命题(只需写出一种情况).
AE=AD ②AB=AC ③OB=OC ④∠B=∠C.
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且,BC=1,连结BF,分别交AC、DC、DE于点P、Q、R.
(1)求证:∽,并求出BF的长.
(2)观察图形,请你提出一个与点P相关的问题,并进行解答.
阅读材料,解答问题:
材料:“小聪设计的一个电子游戏是:一电子跳蚤从P1(-3,9)开始,按点的横坐标依次增加1的规律,在抛物线y=x2上向右跳动,得到点P2、P3、P4、P5…(如图①所示),过P1、P2、P3分别作P1H2、P2H2、P3H3垂直于x轴,垂足为H1、H2、H3,
则,即的面积为1”
问题:
(1)求四边形和四边形的面积(要求:写出其中一个四边形面积的求解过程,另一个直接写出答案);
(2)猜想四边形的面积,并说明理由(利用图②).
(3)若将抛物线改为抛物线,其他条件不变,猜想四边形的面积(直接写出答案).
① ②
中考冲刺第4讲 开放型问题 模块一:条件开放型 中考冲刺 4级 ★★★★☆
模块二:结论开放型
模块三:方法开放型
(1)如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是 .(只填一个即可)
(2)写出一个在三视图中俯视图与主视图完全相同的几何体 .
(3)如图,菱形ABCD中,对角线AC、BD相交于点O,不添加任何辅助线,请添加一个条件 ,使四边形ABCD是正方形(填一个即可).
【练习1】如图,AB,CD相交于点E,且AB=CD,试添加一个条件使得△ADE≌△CBE.现给出如下五个条件:①∠A=∠C;②∠B=∠D;③AE=CE;④BE=DE;⑤AD=CB.其中符合要求有( )
A. 2个 B. 3个 C. 4个 D. 5个
先化简:,再用一个你最喜欢的数代替计算结果.
【练习2】先化简,然后从的范围内选择一个合适的整数作为x的值代入求值.
已知一个函数,当时,函数值y随着x的增大而减小,请写出这个函数关系式__________.
【练习3】对于两个二次函数,,满足.当时,二次函数的函数值为5,且二次函数有最小值3.请写出两个符合题意的二次函数的解析式__________ (要求:写出的解析式的对称轴不能相同).
如图,AB是⊙O的弦,OC⊥AB于C,连接OA、OB,点P是半径OB上任意一点,连接AP.若OA=5cm,OC=3cm,则AP的长度可能是 6
cm(写出一个符合条件的数值即可)
【练习4】如图,AB是⊙O的直径,弦BC=4cm,F是弦BC的中点,∠ABC=60°.若动点E以1cm/s的速度从A点出发在AB上沿着A→B→A运动,设运动时间为t(s)(0≤t<16),连接EF,当t为______时,△BEF是直角三角形。4s
【例题5】如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连结BE交AC于点F,连结DF.
(1)证明:△CBF≌△CDF;
(2)若AC=,BD=2,求四边形ABCD的周长;
(3)请你添加一个条件,使得∠EFD=∠BAD,并予以证明.
【练习5】如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.
(1)求证:四边形EGFH是矩形;
(2)小明在完成(1)的证明后继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.
【例题6】在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.
请你从这四个条件中选出三个作为题设,另一个作为结论,
组成一个真命题,并给予证明.
题设: ;结论: .(均填写序号)
证明:
【练习6】如图,在△AEC和△DFB中,∠E=∠F,点A、B、C、D在同一直线上,有如下三个关系式:①AE∥DF,②AB=CD,③CE=BF.
(1)请用其中两个关系式作为条件,另一个作为结论,写出你认为正确的所有命题(用序号写出命题书写形式:“如果…,那么…”)
(2)选择(1)中你写出的一个命题,说明它正确的理由.
【例题7】如图,在中,点D、E分别在边BC、AC上,连接AD、DE,且∠1=∠B=∠C.
(1)由题设条件,请写出三个正确结论:(要求不再添加其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)
答:结论一: ;
结论二: ;
结论三: .
(2)若∠B=45°,BC=2,当点D在BC上运动时(点D不与B、C重合),
①求CE的最大值;
②若△ADE是等腰三角形,求此时BD的长.
(注意:在第(2)的求解过程中,若有运用(1)中得出的结论,须加以证明)
【练习7-1】问题情境:将一副直角三角板(Rt△ABC和Rt△DEF)按图1所示的方式摆放,其中∠ACB=90°,CA=CB,∠FDE=90°,O是AB的中点,点D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量关系,并说明理由.
探究展示:小宇同学展示出如下正确的解法:
解:OM=ON,证明如下:
连接CO,则CO是AB边上中线,
∵CA=CB,∴CO是∠ACB的角平分线.(依据1)
∵OM⊥AC,ON⊥BC,∴OM=ON.(依据2)
反思交流:
(1)上述证明过程中的“依据1”和“依据2”分别是指:
依据1:
依据2:
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
拓展延伸:
(3)将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置,使点D落在BA的延长线上,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连接OM、ON,试判断线段OM、ON的数量关系与位置关系,并写出证明过程.
【练习7-2】在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变,如图2、图3,线段BE、EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.
【例题8】阅读理解:我们把对非负实数 “四舍五入”到个位的值记为《》,即当为非负整数时,若,则《》=n.例如:《0.67》=1,《2.49》=2,….给出下列关于《》的问题:其中正确结论的个数是( )
①《》=2;
②《2》=2《》;
③当为非负整数时,《》=+《2》;
④若《》=5,则实数x的取值范围是;
⑤满足《》=的非负实数有三个.
A.1 B.2 C.3 D.4
【练习8-1】如图,已知AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,AE的延长线交BC于点F,连接AD、BD.给出以下结论:①AD∥OC;②FC=FE;③点E为的内心.其中正确的是________________(填序号)
【练习8-2】图AB是⊙O的直径,BC是⊙O弦OD⊥CB于点E,交于点D
(1)请写出三个不同类型的正确结论:
(2)连结CD,设,,求、的关系
解题思路及方法:
找特征(中点、特殊角、折叠等),找模型:相似(母子型、A字型、八字型)三线合一、面积等;
借助问与问之间的联系,寻找条件和思路。
照搬:照搬上一问的方法,思路解决问题,如照搬字母、辅助线、全等、相似等。
找结构:寻找不变的结构,利用不变结构的特征解决问题。
【例题9】阅读理解:
我们把满足某种条件的所有点所组成的图形,叫做符合这个条件的点的轨迹.
例如:角的平分线是到角的两边距离相等的点的轨迹.
问题:如图1,已知EF为△ABC的中位线,M是边BC上一动点,连接AM交EF于点P,那么动点P为线段AM中点.
理由:∵线段EF为△ABC的中位线,∴EF∥BC,
由平行线分线段成比例得:动点P为线段AM中点.
由此你得到动点P的运动轨迹是:______.
知识应用:如图2,已知EF为等边△ABC边AB、AC上的动点,连结EF;若AF=BE,且等边△ABC的边长为8,求线段EF中点Q的运动轨迹的长.
拓展提高:如图3,P为线段AB上一动点(点P不与点A、B重合),在线段AB的同侧分别作等边△APC和等边△PBD,连结AD、BC,交点为Q.
(1)求∠AQB的度数;
(2)若AB=6,求动点Q运动轨迹的长.
【例题10】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得:的值为常数,则= .
如图,若AC、BD、EF两两互相平分于点O,请写出图中的一对全等三角形(只需写一对即可)_________.
如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是______.(注:将你认为正确的结论都填上)
如图,已知AC=DB,要使△ABC≌△DCB,只需增加的一个条件是_________或_________.
如图,下面四个条件中,请你以其中两个为已知条件,第三个为结论,推出一个正确的命题(只需写出一种情况).
AE=AD ②AB=AC ③OB=OC ④∠B=∠C.
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且,BC=1,连结BF,分别交AC、DC、DE于点P、Q、R.
(1)求证:∽,并求出BF的长.
(2)观察图形,请你提出一个与点P相关的问题,并进行解答.
阅读材料,解答问题:
材料:“小聪设计的一个电子游戏是:一电子跳蚤从P1(-3,9)开始,按点的横坐标依次增加1的规律,在抛物线y=x2上向右跳动,得到点P2、P3、P4、P5…(如图①所示),过P1、P2、P3分别作P1H2、P2H2、P3H3垂直于x轴,垂足为H1、H2、H3,
则,即的面积为1”
问题:
(1)求四边形和四边形的面积(要求:写出其中一个四边形面积的求解过程,另一个直接写出答案);
(2)猜想四边形的面积,并说明理由(利用图②).
(3)若将抛物线改为抛物线,其他条件不变,猜想四边形的面积(直接写出答案).
① ②
同课章节目录
