2023-2024学年华东师大版八年级数学上册13.4.4尺规作图(第2课时)课件(共24页PPT)
文档属性
| 名称 | 2023-2024学年华东师大版八年级数学上册13.4.4尺规作图(第2课时)课件(共24页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 14:54:43 | ||
图片预览





文档简介
(共24张PPT)
华东师大版·八年级数学上册
2.尺规作图(2)
回顾已经学过的基本作图有哪几种?
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作已知角的平分线.
新课引入
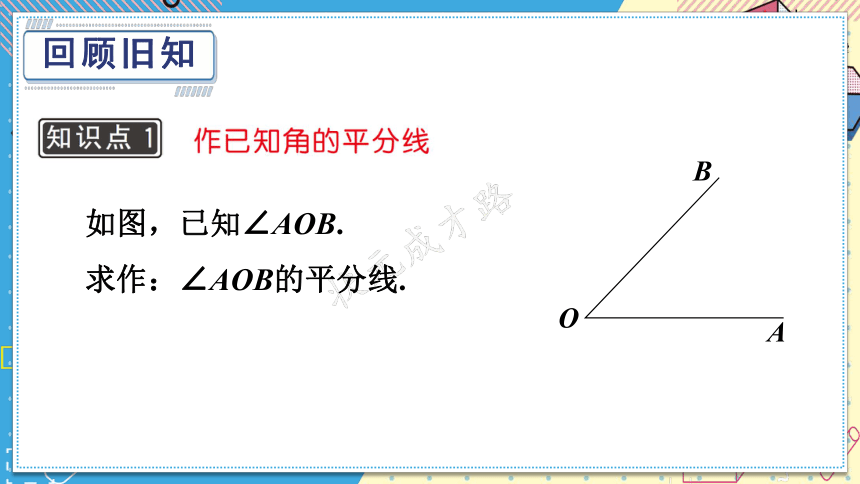
回顾旧知
A
O
B
如图,已知∠AOB.
求作:∠AOB的平分线.
A
O
B
作法:
(1)在射线OA、OB上分别截取OD、OE,使OD=OE;
D
E
(2)分别以点D,E为圆心、大于线段DE长的一半为半径画弧,在∠AOB内两弧交于点C;
C
(3)作射线OC.
则射线OC就是所求作的∠AOB的平分线.
否则得不到点C或交点C不明显.
A
O
B
D
E
C
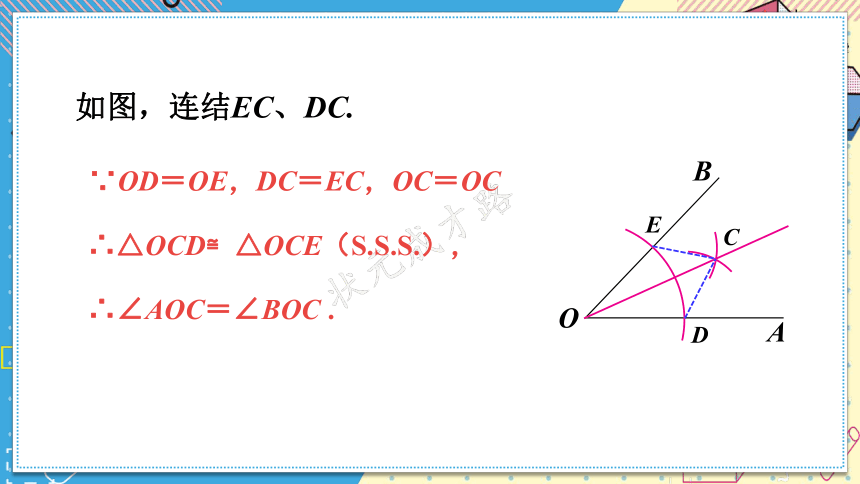
如图,连结EC、DC.
∵OD=OE,DC=EC,OC=OC
∴△OCD≌△OCE(S.S.S.),
∴∠AOC=∠BOC .
探究
经过一已知点作已知直线的垂线有可以分为几种情况?
可分为两种情况来讨论:
经过已知直线上一点作已知直线的垂线.
经过已知直线外一点作已知直线的垂线.
思考
如何经过一已知点作已知直线的垂线呢?
新知学习
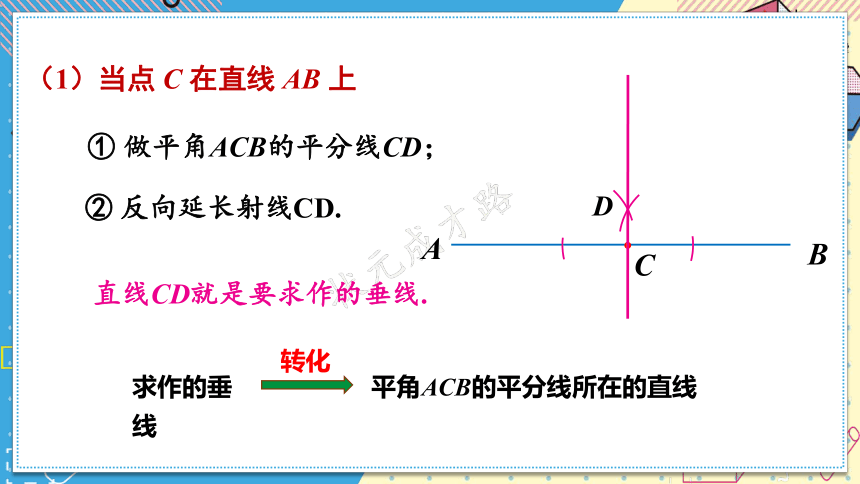
(1)当点 C 在直线 AB 上
C
B
A
① 做平角ACB的平分线CD;
D
② 反向延长射线CD.
直线CD就是要求作的垂线.
求作的垂线
平角ACB的平分线所在的直线
转化
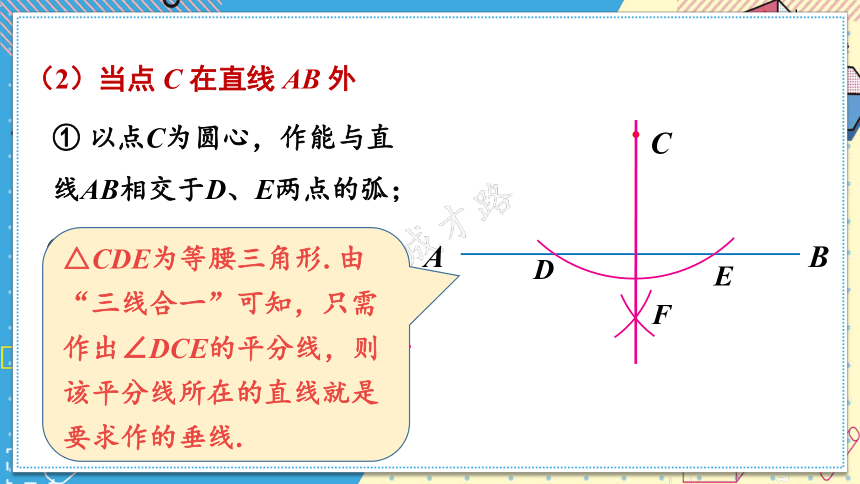
(2)当点 C 在直线 AB 外
C
B
A
① 以点C为圆心,作能与直线AB相交于D、E两点的弧;
D
E
②作∠DCE的平分线.
F
直线CF就是要求作的垂线.
△CDE为等腰三角形. 由“三线合一”可知,只需作出∠DCE的平分线,则该平分线所在的直线就是要求作的垂线.
经过一已知点
作已知直线的垂线
经过已知直线上一点作已知直线的垂线,实质是作一个平角的平分线,并将角的平分线反向延长.
经过已知直线外一点作已知直线的垂线,实质是作以直线外这一点为顶点,底在直线上的等腰三角形的顶角的平分线.
利用直尺和圆规作一个等于45°的角.
作法:
(1)作直线AB;
B
A
(2)过点A作直线AB的垂线AC;
C
(3)作∠CAB的平分线AD.
D
∠DAB就是要求作的角.
练 习
1. 如图,点P在∠O的一边上,试过点P作该角两边的垂线.
O
P
A
B
2.已知△ABC,利用尺规作图,作BC边上的高AD,正确的是( )
B
如图,作△ABC边BC上的高.
A
B
C
D
AD就是要求作的高.
3.如图,AE∥BF,AC平分∠BAE,交BF于点C.
(1)尺规作图:过点B作AC的垂线,交AC于点O,交AE于点D;(保留作图痕迹,不写作法)
解:(1)如题图所示,BO即为所求作的垂线.
4.如图,AE∥BF,AC平分∠BAE,交BF于点C.(2)在(1)的图形中,找出三条相等的线段,并予以证明.解:(2)AB=AD=BC.证明:∵AE∥BF,∴∠EAC=∠BCA.∵AC平分∠BAE,∴∠EAC=∠BAC,∴∠BCA=∠BAC,∴BA=BC.∵BD⊥AO,AO平分∠BAD,∴AB=AD. ∴AB=AD=BC.
思考
如图,已知直线l是线段AB的垂直平分线,则直线l是线段AB的对称轴,
对l上的任意两点C、D,总有:
A
B
D
C
l
CA=CB,DA=DB
由此,你能发现作垂直平分线的方法吗
已知:如图,线段AB.
求作:线段AB的垂直平分线CD.
B
A
作法:
(1)分别以点A和点B为圆心、大于AB一半的长为半径作圆弧,两弧相交于点C和点D;
C
D
(2)作直线CD.
直线CD就是要求作的线段AB的垂直平分线.
如何证明直线CD垂直平分线段AB?
B
A
C
D
B
A
C
D
如图,连结CA、CB、DA、DB.
∵AC=BC,AD=BD,CD=CD,
∴△ACD≌△BCD(S.S.S.),
∴∠ACD=∠BCD .
∴CD垂直平分线段AB(等腰三角形的“三线合一”).
B
A
C
D
线段AB的中点
①找线段中点
②作任意三角形的三边的中线
B
A
练 习
1. 四等分已知线段AB.
2.如图,作△ABC的边BC的垂直平分线.
A
B
C
E
F
直线EF就是要求作的垂直平分线.
课堂小结
过直线上一点作垂线
过直线外一点作垂线
课堂小结
(1)分别以已知线段的两个端点为圆心、大于这两点的距离的一半为半径画弧,两弧相交于两点
(2)过这两个交点作直线
(3)该直线就是线段的垂直平分线
华东师大版·八年级数学上册
2.尺规作图(2)
回顾已经学过的基本作图有哪几种?
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作已知角的平分线.
新课引入
回顾旧知
A
O
B
如图,已知∠AOB.
求作:∠AOB的平分线.
A
O
B
作法:
(1)在射线OA、OB上分别截取OD、OE,使OD=OE;
D
E
(2)分别以点D,E为圆心、大于线段DE长的一半为半径画弧,在∠AOB内两弧交于点C;
C
(3)作射线OC.
则射线OC就是所求作的∠AOB的平分线.
否则得不到点C或交点C不明显.
A
O
B
D
E
C
如图,连结EC、DC.
∵OD=OE,DC=EC,OC=OC
∴△OCD≌△OCE(S.S.S.),
∴∠AOC=∠BOC .
探究
经过一已知点作已知直线的垂线有可以分为几种情况?
可分为两种情况来讨论:
经过已知直线上一点作已知直线的垂线.
经过已知直线外一点作已知直线的垂线.
思考
如何经过一已知点作已知直线的垂线呢?
新知学习
(1)当点 C 在直线 AB 上
C
B
A
① 做平角ACB的平分线CD;
D
② 反向延长射线CD.
直线CD就是要求作的垂线.
求作的垂线
平角ACB的平分线所在的直线
转化
(2)当点 C 在直线 AB 外
C
B
A
① 以点C为圆心,作能与直线AB相交于D、E两点的弧;
D
E
②作∠DCE的平分线.
F
直线CF就是要求作的垂线.
△CDE为等腰三角形. 由“三线合一”可知,只需作出∠DCE的平分线,则该平分线所在的直线就是要求作的垂线.
经过一已知点
作已知直线的垂线
经过已知直线上一点作已知直线的垂线,实质是作一个平角的平分线,并将角的平分线反向延长.
经过已知直线外一点作已知直线的垂线,实质是作以直线外这一点为顶点,底在直线上的等腰三角形的顶角的平分线.
利用直尺和圆规作一个等于45°的角.
作法:
(1)作直线AB;
B
A
(2)过点A作直线AB的垂线AC;
C
(3)作∠CAB的平分线AD.
D
∠DAB就是要求作的角.
练 习
1. 如图,点P在∠O的一边上,试过点P作该角两边的垂线.
O
P
A
B
2.已知△ABC,利用尺规作图,作BC边上的高AD,正确的是( )
B
如图,作△ABC边BC上的高.
A
B
C
D
AD就是要求作的高.
3.如图,AE∥BF,AC平分∠BAE,交BF于点C.
(1)尺规作图:过点B作AC的垂线,交AC于点O,交AE于点D;(保留作图痕迹,不写作法)
解:(1)如题图所示,BO即为所求作的垂线.
4.如图,AE∥BF,AC平分∠BAE,交BF于点C.(2)在(1)的图形中,找出三条相等的线段,并予以证明.解:(2)AB=AD=BC.证明:∵AE∥BF,∴∠EAC=∠BCA.∵AC平分∠BAE,∴∠EAC=∠BAC,∴∠BCA=∠BAC,∴BA=BC.∵BD⊥AO,AO平分∠BAD,∴AB=AD. ∴AB=AD=BC.
思考
如图,已知直线l是线段AB的垂直平分线,则直线l是线段AB的对称轴,
对l上的任意两点C、D,总有:
A
B
D
C
l
CA=CB,DA=DB
由此,你能发现作垂直平分线的方法吗
已知:如图,线段AB.
求作:线段AB的垂直平分线CD.
B
A
作法:
(1)分别以点A和点B为圆心、大于AB一半的长为半径作圆弧,两弧相交于点C和点D;
C
D
(2)作直线CD.
直线CD就是要求作的线段AB的垂直平分线.
如何证明直线CD垂直平分线段AB?
B
A
C
D
B
A
C
D
如图,连结CA、CB、DA、DB.
∵AC=BC,AD=BD,CD=CD,
∴△ACD≌△BCD(S.S.S.),
∴∠ACD=∠BCD .
∴CD垂直平分线段AB(等腰三角形的“三线合一”).
B
A
C
D
线段AB的中点
①找线段中点
②作任意三角形的三边的中线
B
A
练 习
1. 四等分已知线段AB.
2.如图,作△ABC的边BC的垂直平分线.
A
B
C
E
F
直线EF就是要求作的垂直平分线.
课堂小结
过直线上一点作垂线
过直线外一点作垂线
课堂小结
(1)分别以已知线段的两个端点为圆心、大于这两点的距离的一半为半径画弧,两弧相交于两点
(2)过这两个交点作直线
(3)该直线就是线段的垂直平分线
