1.2.1 代入消元法 课件(共26张PPT)
文档属性
| 名称 | 1.2.1 代入消元法 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 08:42:05 | ||
图片预览








文档简介
(共26张PPT)
1.2 二元一次方程组的解法
1.2.1 代入消元法
1.会用代入消元法解简单的二元一次方程组.
2.经历探索代入消元法解二元一次方程的过程,理解代 入消元法的基本思想所体现的化归思想方法.
3.通过提供适当的情境资料,吸引学生的注意力,激发学生的学习兴趣;在合作讨论中学会交流与合作,培养良好的数学思想,逐步渗透类比、化归的意识.
【教学重点】
用代入消元法解二元一次方程组.
【教学难点】
探索如何用代入消元法解二元一次方程组,感受“消元”思想.
1、什么是二元一次方程组
2、如何求解二元一次方程组呢?(和同学们一起交流讨论一下)
把两个含有相同未知数的二元一次方程(或者一个二元一次方程、一个一元一次方程)联立起来,组成的方程组,叫做二元一次方程组。
提示:尝试转化为我们学过的一元一次方程求解。
我们家1月份的天然气费和水费共60元,其中天然气费比水费多20元.你知道天然气费和水费各是多少吗
问题中既要求水费,又要求天然气费,可以设1月份的天然气费是x元,水费是y元.
根据题意得:
x+y=60, ①
x-y=20, ②
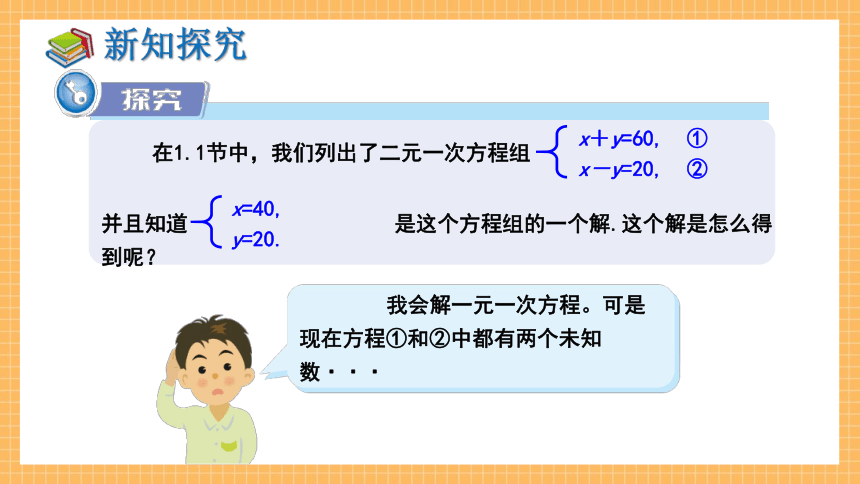
在1.1节中,我们列出了二元一次方程组
x+y=60, ①
x-y=20, ②
并且知道 是这个方程组的一个解.这个解是怎么得到呢?
x=40,
y=20.
我会解一元一次方程。可是现在方程①和②中都有两个未知数···
由②式可得
x+y=60, ①
x-y=20,②
二元一次方程组
解:设1月份的天然气费是x元,水费是y元.
x=y+20. ③
于是可以把③代入①式,得
( y+20 )+y=60. ④
解方程④,得
y=_______
将y的值代入③式 ,得
x=_______
因此原方程组的解是
x=40,
y=20.
20
40
求方程组解的过程叫做解方程组.
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
同桌同学讨论,解二元一次方程组的基本思想法是什么?
消元(消去一个未知数)
二元一次方程组
一元一次方程
转化
1.把下列方程改写成为用含x的代数式表示y的形式.
(1)2x-y=﹣1
(2)x+2y-2=0
解: 2x-(﹣1)=y
y=2x+1
解: 2y=2-x
y= x+1
【例1】解二元一次方程组:
②
①
解:由②式得y= -3x+1. ③
把③代入①式,得5x-(-3x+1)=-9.
解得 x= -1.
把x= -1代入③式,得 y=4.
因此原方程组的解是
可以把求得的x,y的值代入原方程组检验,看是否为方程组的解.
转化
代入
求解
回代
写解
注意:检验方程组的解.
代入消元法
在上面的例子中,消去一个未知数的方法是:把其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入另一个方程中,便得到一个一元一次方程,这种解方程组的方法称为代入消元法,简称代入法。
代入法是解二元一次方程组常用的方法之一.
【例2】用代入法解方程组:
②
①
解:由①式得 ③
把③代入②式,得
解得 y=2.
把y=2代入③式,得 x=3.
因此原方程组的解是:
在例2中,用含x的代数式表示y来解方程组.
2x-3y=0,①
5x+7y=1.②
解:由①式可得
于是可以把③代入②式,得
解得
y=2.
将y=2代入③式 ,得
x=3.
因此原方程组的解是
x=3,
y=2.
③
解:由①式可得
于是可以把④代入②式,得
解得
x=3.
将x=3代入③式 ,得
y=2.
因此原方程组的解是
x=3,
y=2.
④
解:由①得 y = 8-x. ③
将③代入②得
5x + 3(8-x) = 34.
解得 x = 5.
把 x = 5 代入③得 y = 3.
x + y = 8,①
5x + 3y = 34. ②
解二元一次方程组:
所以原方程组的解为
x = 5,
y = 3.
注意:用代入消元法解二元一次方程组时,
选取一个未知数的系数是1的方程进行变形;
若未知数的系数都不是,则选取系数的绝对值较小的方程变形;
观察上面的方程和方程组,你能发现二者之间的联系吗?请你尝试求得方程组的解.(先试着独立完成,然后与你的同伴交流做法)
1.为什么能替换?
代表了同一个量
二元一次方程组 一元一次方程
消元
2.代入前后的方程组发生了怎样的变化 (代入的作用)
化归思想
等量代换
例3 根据市场调查,某种消毒液的大瓶装 (500 g) 和小瓶装 (250 g) 两种产品的销售数量 (按瓶计算) 比为 2∶5.某厂每天生产这种消毒液 22.5 t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
等量关系:
(1) 大瓶数
小瓶数
(2) 大瓶所装消毒液
小瓶所装消毒液
总生产量.
解:设这些消毒液应该分装 x 大瓶、y 小瓶.
根据题意可列方程组
解得 x = 20000.
把 x = 20000 代入 ,得 y = 50000.
③
答:这些消毒液应该分装 20000 大瓶和 50000 小瓶.
①
②
í
ì
=
+
=
22500000.
250
500
2
5
y
x
y,
x
③
①
由 得 .
把 代入 得 .
③
②
用代入消元法解二元一次方程组的一般步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的式子表示出来;
第二步:把此式子代入没有变形的另一个方程中,可得一个一元一次方程;
第三步:解这个一元一次方程,得到一个未知数的值;
第四步:回代求出另一个未知数的值;
第五步:把方程组的解表示出来;
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.
1、判断。
(1)任何二元一次方程组都能用代入消元法求.( )
(2)用代入消元法解二元一次方程组时,尽可能选择系数比较简单的一个方程进行变形.( )
对
对
y = 2x,
x + y = 12;
(1)
(2)
2x = y - 5,
4x + 3y = 65.
解:
(1)
x = 4,
y = 8.
(2)
2.用代入消元法解下列方程组.
x = 5,
y = 15.
3.若方程 5x2m+n + 4y3m-2n = 9 是关于 x、y 的二元一次方程,求 m 、n 的值.
解:
由题意可列方程组
2m + n = 1
3m - 2n = 1
①
②
由①得
把③代入②得
n = 1 - 2m.
③
3m – 2(1 – 2m) = 1.
把 m 代入 ③,得
4.篮球联赛中,每场比赛都要分出胜负,胜一场得 2 分.负一场得 1 分,某队为了争取较好的名次,想在全部 20 场比赛中得到 35 分,那么这个队胜负场数分别是多少?
解:设胜的场数是x,负的场数是y,可列方程组:
由①得 y=20 - x .
将③代入②,得 2x + 20 - x = 35 ,
解得 x = 15.
将 x = 15 代入③得 y = 5. 则这个方程组的解是
答:这个队胜 15 场,负 5 场.
①
②
5. 李大叔去年承包了 10 亩地种植甲、乙两种蔬菜,共
获利 18000 元,其中甲种蔬菜每亩获利 2000 元,乙种蔬菜每亩获利 1500 元,李大叔去年甲、乙两种蔬菜各
种植了多少亩?
解:设甲、乙两种蔬菜各种植了x、y亩,依题意得:
x + y = 10, ①
2000x + 1500y = 18000. ②
由①得 y = 10 - x. ③
将③代入②,得 2000x + 1500(10 - x) = 18000,
解得 x = 6.将 x = 6 代入③,得 y = 4.
答:李大叔去年甲、乙两种蔬菜各种植了 6 亩、4 亩.
1.消元实质
二元一次方程组
消 元
代入法
一元一次方程
2.代入法的一般步骤
即:
变形
代替
回代
写解
3.能灵活运用适当方法解二元一次方程组
变
代
求
写
习题1.2
第1题
1.2 二元一次方程组的解法
1.2.1 代入消元法
1.会用代入消元法解简单的二元一次方程组.
2.经历探索代入消元法解二元一次方程的过程,理解代 入消元法的基本思想所体现的化归思想方法.
3.通过提供适当的情境资料,吸引学生的注意力,激发学生的学习兴趣;在合作讨论中学会交流与合作,培养良好的数学思想,逐步渗透类比、化归的意识.
【教学重点】
用代入消元法解二元一次方程组.
【教学难点】
探索如何用代入消元法解二元一次方程组,感受“消元”思想.
1、什么是二元一次方程组
2、如何求解二元一次方程组呢?(和同学们一起交流讨论一下)
把两个含有相同未知数的二元一次方程(或者一个二元一次方程、一个一元一次方程)联立起来,组成的方程组,叫做二元一次方程组。
提示:尝试转化为我们学过的一元一次方程求解。
我们家1月份的天然气费和水费共60元,其中天然气费比水费多20元.你知道天然气费和水费各是多少吗
问题中既要求水费,又要求天然气费,可以设1月份的天然气费是x元,水费是y元.
根据题意得:
x+y=60, ①
x-y=20, ②
在1.1节中,我们列出了二元一次方程组
x+y=60, ①
x-y=20, ②
并且知道 是这个方程组的一个解.这个解是怎么得到呢?
x=40,
y=20.
我会解一元一次方程。可是现在方程①和②中都有两个未知数···
由②式可得
x+y=60, ①
x-y=20,②
二元一次方程组
解:设1月份的天然气费是x元,水费是y元.
x=y+20. ③
于是可以把③代入①式,得
( y+20 )+y=60. ④
解方程④,得
y=_______
将y的值代入③式 ,得
x=_______
因此原方程组的解是
x=40,
y=20.
20
40
求方程组解的过程叫做解方程组.
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
同桌同学讨论,解二元一次方程组的基本思想法是什么?
消元(消去一个未知数)
二元一次方程组
一元一次方程
转化
1.把下列方程改写成为用含x的代数式表示y的形式.
(1)2x-y=﹣1
(2)x+2y-2=0
解: 2x-(﹣1)=y
y=2x+1
解: 2y=2-x
y= x+1
【例1】解二元一次方程组:
②
①
解:由②式得y= -3x+1. ③
把③代入①式,得5x-(-3x+1)=-9.
解得 x= -1.
把x= -1代入③式,得 y=4.
因此原方程组的解是
可以把求得的x,y的值代入原方程组检验,看是否为方程组的解.
转化
代入
求解
回代
写解
注意:检验方程组的解.
代入消元法
在上面的例子中,消去一个未知数的方法是:把其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入另一个方程中,便得到一个一元一次方程,这种解方程组的方法称为代入消元法,简称代入法。
代入法是解二元一次方程组常用的方法之一.
【例2】用代入法解方程组:
②
①
解:由①式得 ③
把③代入②式,得
解得 y=2.
把y=2代入③式,得 x=3.
因此原方程组的解是:
在例2中,用含x的代数式表示y来解方程组.
2x-3y=0,①
5x+7y=1.②
解:由①式可得
于是可以把③代入②式,得
解得
y=2.
将y=2代入③式 ,得
x=3.
因此原方程组的解是
x=3,
y=2.
③
解:由①式可得
于是可以把④代入②式,得
解得
x=3.
将x=3代入③式 ,得
y=2.
因此原方程组的解是
x=3,
y=2.
④
解:由①得 y = 8-x. ③
将③代入②得
5x + 3(8-x) = 34.
解得 x = 5.
把 x = 5 代入③得 y = 3.
x + y = 8,①
5x + 3y = 34. ②
解二元一次方程组:
所以原方程组的解为
x = 5,
y = 3.
注意:用代入消元法解二元一次方程组时,
选取一个未知数的系数是1的方程进行变形;
若未知数的系数都不是,则选取系数的绝对值较小的方程变形;
观察上面的方程和方程组,你能发现二者之间的联系吗?请你尝试求得方程组的解.(先试着独立完成,然后与你的同伴交流做法)
1.为什么能替换?
代表了同一个量
二元一次方程组 一元一次方程
消元
2.代入前后的方程组发生了怎样的变化 (代入的作用)
化归思想
等量代换
例3 根据市场调查,某种消毒液的大瓶装 (500 g) 和小瓶装 (250 g) 两种产品的销售数量 (按瓶计算) 比为 2∶5.某厂每天生产这种消毒液 22.5 t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
等量关系:
(1) 大瓶数
小瓶数
(2) 大瓶所装消毒液
小瓶所装消毒液
总生产量.
解:设这些消毒液应该分装 x 大瓶、y 小瓶.
根据题意可列方程组
解得 x = 20000.
把 x = 20000 代入 ,得 y = 50000.
③
答:这些消毒液应该分装 20000 大瓶和 50000 小瓶.
①
②
í
ì
=
+
=
22500000.
250
500
2
5
y
x
y,
x
③
①
由 得 .
把 代入 得 .
③
②
用代入消元法解二元一次方程组的一般步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的式子表示出来;
第二步:把此式子代入没有变形的另一个方程中,可得一个一元一次方程;
第三步:解这个一元一次方程,得到一个未知数的值;
第四步:回代求出另一个未知数的值;
第五步:把方程组的解表示出来;
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.
1、判断。
(1)任何二元一次方程组都能用代入消元法求.( )
(2)用代入消元法解二元一次方程组时,尽可能选择系数比较简单的一个方程进行变形.( )
对
对
y = 2x,
x + y = 12;
(1)
(2)
2x = y - 5,
4x + 3y = 65.
解:
(1)
x = 4,
y = 8.
(2)
2.用代入消元法解下列方程组.
x = 5,
y = 15.
3.若方程 5x2m+n + 4y3m-2n = 9 是关于 x、y 的二元一次方程,求 m 、n 的值.
解:
由题意可列方程组
2m + n = 1
3m - 2n = 1
①
②
由①得
把③代入②得
n = 1 - 2m.
③
3m – 2(1 – 2m) = 1.
把 m 代入 ③,得
4.篮球联赛中,每场比赛都要分出胜负,胜一场得 2 分.负一场得 1 分,某队为了争取较好的名次,想在全部 20 场比赛中得到 35 分,那么这个队胜负场数分别是多少?
解:设胜的场数是x,负的场数是y,可列方程组:
由①得 y=20 - x .
将③代入②,得 2x + 20 - x = 35 ,
解得 x = 15.
将 x = 15 代入③得 y = 5. 则这个方程组的解是
答:这个队胜 15 场,负 5 场.
①
②
5. 李大叔去年承包了 10 亩地种植甲、乙两种蔬菜,共
获利 18000 元,其中甲种蔬菜每亩获利 2000 元,乙种蔬菜每亩获利 1500 元,李大叔去年甲、乙两种蔬菜各
种植了多少亩?
解:设甲、乙两种蔬菜各种植了x、y亩,依题意得:
x + y = 10, ①
2000x + 1500y = 18000. ②
由①得 y = 10 - x. ③
将③代入②,得 2000x + 1500(10 - x) = 18000,
解得 x = 6.将 x = 6 代入③,得 y = 4.
答:李大叔去年甲、乙两种蔬菜各种植了 6 亩、4 亩.
1.消元实质
二元一次方程组
消 元
代入法
一元一次方程
2.代入法的一般步骤
即:
变形
代替
回代
写解
3.能灵活运用适当方法解二元一次方程组
变
代
求
写
习题1.2
第1题
