1.1 建立二元一次方程组 课件(共35张PPT)
文档属性
| 名称 | 1.1 建立二元一次方程组 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 08:42:05 | ||
图片预览








文档简介
(共35张PPT)
1.1 建立二元一次方程组
1.理解二元一次方程、二元一次方程组和它的解的含义;
2.会检验一对数是不是某个二元一次方程组的解;
3.能根据问题情境列二元一次方程组.
【教学重点】
二元一次方程组和它的解的概念.
【教学难点】
二元一次方程组的解的概念.
2.像方程2.5x+318=1068,2.4y+2y+2.4=6.8这样,只____________,
并且______________,这样的方程叫做一元一次方程.
含有一个未知数
未知数的次数是1
1.我们把含有未知数的______叫方程.
等式
3. 一般地,等式具有下述性质:
(1)等式的两边都_____(或减去)_____数(或式),所得结果仍是等式.
(2)等式的两边都乘(或____)同一个_______________________,所得结果仍是______.
加上
同一个
除以
数(或式)
除数或除式不能为0
等式
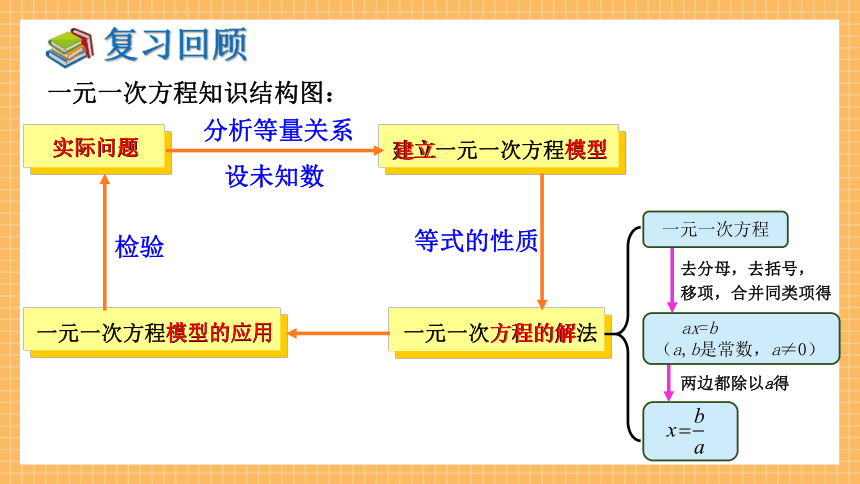
实际问题
建立一元一次方程模型
一元一次方程的解法
一元一次方程模型的应用
等式的性质
检验
分析等量关系
设未知数
一元一次方程知识结构图:
去分母,去括号,
移项,合并同类项得
两边都除以a得
ax=b
(a,b是常数,a≠0)
一元一次方程
实际问题
建立
模型的应用
方程的解
模型
二元一次方程组的定义
问题1:依据章引言的问题如何列一元一次方程?
解:设胜 x 场,则负 (10-x) 场.
引言:篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2 分,负一场得 1 分.某队在 10 场比赛中得到16 分,那么这个队胜负分别是多少?
2x + (10-x) = 16.
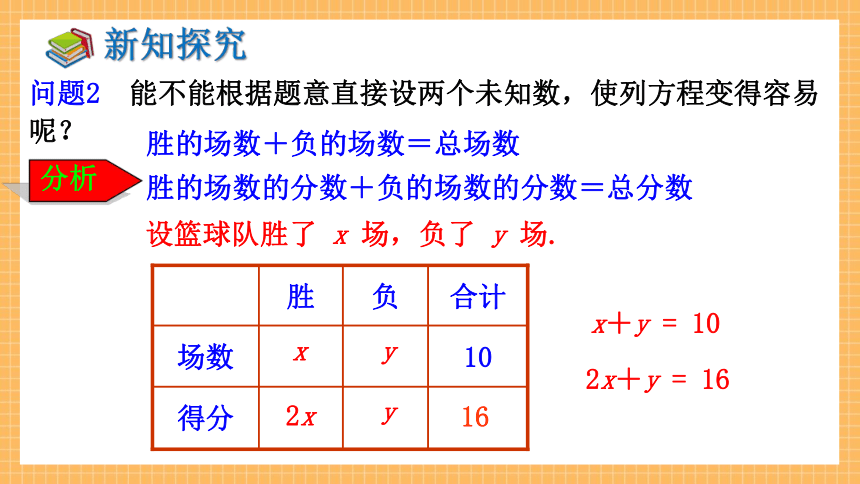
问题2 能不能根据题意直接设两个未知数,使列方程变得容易呢?
分析
胜的场数+负的场数=总场数
胜的场数的分数+负的场数的分数=总分数
设篮球队胜了 x 场,负了 y 场.
得分
10
场数
合计
负
胜
x
y
2x
y
16
2x+y = 16
x+y = 10
思考一:上述方程有什么特点
思考二:它与你学过的一元一次方程比较有什么区别
思考三:你能给它取个名字吗
x+y = 10
2x+y = 16
议一议
含有两个未知数(二元),并且含未知数的项的次数都是 1 的方程叫做二元一次方程.
注意:(1)“一次”是指含未知数的项的次数是1,而不是未知数的次数,如含有 xy 项的方程就不是一次方程;
(2)方程的左右两边都是整式.
(8)4xy+5=0
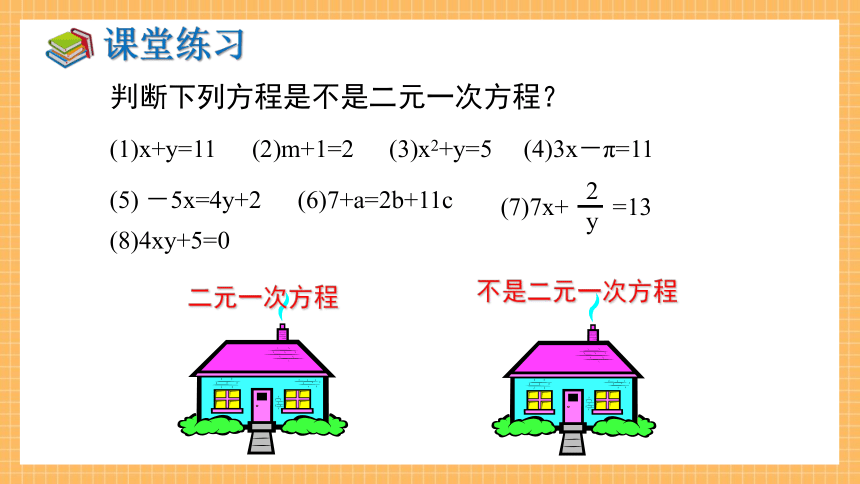
(1)x+y=11
(3)x2+y=5
(2)m+1=2
(4)3x-π=11
(5) -5x=4y+2
(6)7+a=2b+11c
(7)7x+ =13
y
2
二元一次方程
不是二元一次方程
判断下列方程是不是二元一次方程?
判断一个方程是否为二元一次方程的方法:
一看原方程是否是整式方程且只含有两个未知数;
二看整理化简后的方程是否具备两个未知数的系数都不为 0,且含未知数的项的次数都是 1.
方法
例1 已知 |m-1| x | m |+y2n-1=3 是二元一次方程,
则 m+n=_____.
解析:根据题意得 | m |=1 且 |m-1|≠0,2n-1=1,解得 m=-1,n=1,所以 m+n=0.
0
由方程是二元一次方程可知:
(1) 未知数的系数不为 0;
(2) 含未知数的项的次数都是 1.
方法
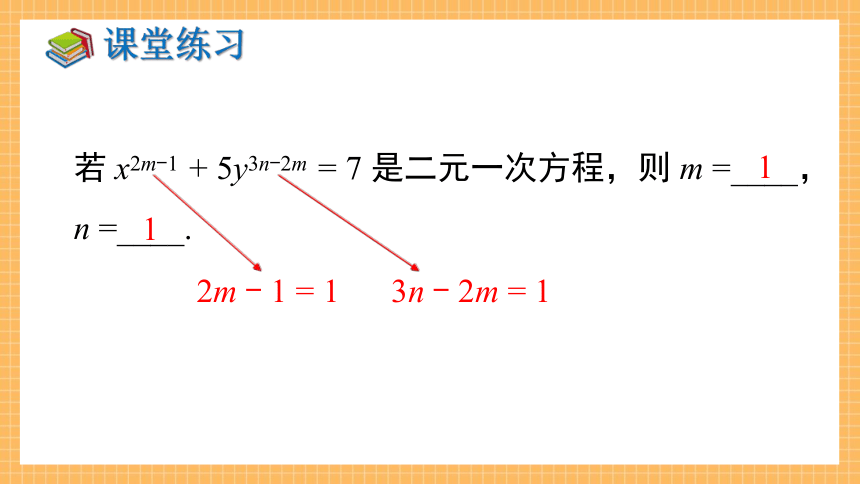
若 x2m-1 + 5y3n-2m = 7 是二元一次方程,则 m =____,n =____.
2m - 1 = 1
1
3n - 2m = 1
1
像这样,把两个含有相同未知数的二元一次方程 (或者一个二元一次方程,一个一元一次方程) 联立起来,组成的方程组,叫做二元一次方程组.
x+y = 10,
2x+y = 16.
叫做方程组
下面方程组是二元一次方程组吗?
(1) (2)
(3) (4)
是
是
不是
不是
x+y=60,
x-y=20
把x=40,y=20代入方程组
的每一个方程中,每
一个方程左、右两边的值相等吗?
40+20= 60,40-20= 20.每一个方程左、右两边的值都相等.
在一个二元一次方程组中,使每一个方程的左、右两边的值都相等的一组未知数的值,叫做这个方程组的一个解.
x+y=60,
x-y=20
把x=40,y=20代入方程组
的每一个方程中,每
一个方程左、右两边的值相等吗?
这个解通常记做
x=40,
y=20.
求方程组的解的过程叫做解方程组.
在一个二元一次方程组中,使每一个方程的左、右两边的值都相等的一组未知数的值,叫做这个方程组的一个解.
一个
一个
?
一个二元一次方程有无数多个解
1. 下列各组数是不是方程 2a = 3b + 20 的解
a = 4,
b = 3;
a = 100,
b = 60.
①
②
不是
是
左边 ≠ 右边
右边 = 3×3 + 20
右边 = 3×60 + 20
左边 = 2×100
左边 = 右边
左边 = 2×4
结论:一般地,二元一次方程有无数个解,而二元一次方程组只有一个解.
2. 二元一次方程组 的解是 ( )
{
x + 2y = 10,
y = 2x
A.{
C.{
D.{
B.{
x = 4,
y = 3
x = 3,
y = 6
x = 2,
y = 4
x = 4,
y = 2
C
小玲在文具店买了3本练习本,2支圆珠笔,共花去8元,其中购买的练习本比圆珠笔多花4元.
(1)为了知道练习本、圆珠笔的单价是多少元,你能列出相应的方程组吗
(2) 是列出的二元一次方程组的解吗?
例
x=2,
y=1
解:(1)设练习本的单价是x元,圆珠笔的单价是y元.
根据题意得:
3x+2y=8, ①
3x-2y=4. ②
(2)把 代入方程①中,左边=右边,
x=2,
y=1
把 代入方程②中,左边=右边,
x=2,
y=1
所以 是方程组 的解.
x=2,
y=1
3x+2y=8,
3x-2y=4.
1. 是上例中方程组的解吗?
解 把 代入方程①中,左边≠右边,
把 代入方程②中,左边≠右边,
所以 不是方程组 的解.
2 若 是方程 x - ky = 1 的解,则 k 的值为
.
{
x = -2,
y = 3
解析:将 代入原方程得 -2 - 3k = 1,解得
k = -1.
{
x = -2,
y = 3
-1
3 加工某种产品须经两道工序,第一道工序每人每天可完成 900 件,第二道工序每人每天可完成 1200 件.现有 7 位工人参加这两道工序,应怎样安排人力,才能使每天第一、二道工序所完成的件数相等?
解:设第一道工序安排 x 人,第二道工序安排 y 人.根据题意得
答:第一道工序安排 4 人,第二道工序安排 3 人.
解这个方程组,得
1. 二元一次方程组 的解是( ).
C
通过计算得 x=1,y=1或“特殊值法”,将A、B、C、D逐一代入方程组检验,只有C项正确,故选C.
解析
x + = 1,
y + x = 2
2. 下列不是二元一次方程组的是 ( )
A.
x + y = 3,
x - y = 1
B.
C.
D.
6x + 4y = 9,
y = 3x + 4
B
x = 1,
x + y = 1
3. 关于 x、y 的方程 ax2 + bx + 2y = 3 是一个二元一次方程,则 a、b 分别满足( )
A. a = 0 且 b = 0 B. a = 0 或 b = 0
C. a = 0 且 b≠0 D. a≠0 且 b≠0
C
4.若关于x,y的二元一次方程组 的解也是二元一次方程2x+3y=6的解,则k的值为( ).
B
解析
由 解得 代入2x+3y=6,
得 ,故选B.
5. 小刘同学用 10 元钱购买了两种不同的贺卡共 8 张, 单价分别是 1 元与 2 元.设他购买了 1 元的贺卡 x 张, 2 元的贺卡 y 张,那么可列方程组 ( )
A. B.
C. D.
D
6.一条船顺流航行,每小时行24km;逆流航行,每小时行18 km.
(1)为了求轮船在静水中的速度x与水的流速y,你能列出相应的方程组吗
解:(1)根据题意得:
x+y=24, ①
x-y=18. ②
(2) 是列出的二元一次方程组的解吗?
x=21,
y=3
(2)把 分别代入方程①②中,方程都是左边=右边,
x=21,
y=3
所以是方程组的解.
7、甲、乙两位同学在解关于的方程组
,乙看错了方程组中的,乙的解为
(1)求出正确的、 的值。
(2)求+的值。
解:(1)把 代入 ② ,得
把 代入①,得
(2)由(1)可知
8.写出方程x+2y=5 在自然数范围内的所有解.
x=1,
y=2
x=3,
y=1
x=5,
y=0
认识二元一次方程组
二元一次方程及二元一次方程组的定义
二元一次方程及二元一次方程组的解
根据实际问题列二元一次方程组
习题1.1
第3 、4 题
1.1 建立二元一次方程组
1.理解二元一次方程、二元一次方程组和它的解的含义;
2.会检验一对数是不是某个二元一次方程组的解;
3.能根据问题情境列二元一次方程组.
【教学重点】
二元一次方程组和它的解的概念.
【教学难点】
二元一次方程组的解的概念.
2.像方程2.5x+318=1068,2.4y+2y+2.4=6.8这样,只____________,
并且______________,这样的方程叫做一元一次方程.
含有一个未知数
未知数的次数是1
1.我们把含有未知数的______叫方程.
等式
3. 一般地,等式具有下述性质:
(1)等式的两边都_____(或减去)_____数(或式),所得结果仍是等式.
(2)等式的两边都乘(或____)同一个_______________________,所得结果仍是______.
加上
同一个
除以
数(或式)
除数或除式不能为0
等式
实际问题
建立一元一次方程模型
一元一次方程的解法
一元一次方程模型的应用
等式的性质
检验
分析等量关系
设未知数
一元一次方程知识结构图:
去分母,去括号,
移项,合并同类项得
两边都除以a得
ax=b
(a,b是常数,a≠0)
一元一次方程
实际问题
建立
模型的应用
方程的解
模型
二元一次方程组的定义
问题1:依据章引言的问题如何列一元一次方程?
解:设胜 x 场,则负 (10-x) 场.
引言:篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2 分,负一场得 1 分.某队在 10 场比赛中得到16 分,那么这个队胜负分别是多少?
2x + (10-x) = 16.
问题2 能不能根据题意直接设两个未知数,使列方程变得容易呢?
分析
胜的场数+负的场数=总场数
胜的场数的分数+负的场数的分数=总分数
设篮球队胜了 x 场,负了 y 场.
得分
10
场数
合计
负
胜
x
y
2x
y
16
2x+y = 16
x+y = 10
思考一:上述方程有什么特点
思考二:它与你学过的一元一次方程比较有什么区别
思考三:你能给它取个名字吗
x+y = 10
2x+y = 16
议一议
含有两个未知数(二元),并且含未知数的项的次数都是 1 的方程叫做二元一次方程.
注意:(1)“一次”是指含未知数的项的次数是1,而不是未知数的次数,如含有 xy 项的方程就不是一次方程;
(2)方程的左右两边都是整式.
(8)4xy+5=0
(1)x+y=11
(3)x2+y=5
(2)m+1=2
(4)3x-π=11
(5) -5x=4y+2
(6)7+a=2b+11c
(7)7x+ =13
y
2
二元一次方程
不是二元一次方程
判断下列方程是不是二元一次方程?
判断一个方程是否为二元一次方程的方法:
一看原方程是否是整式方程且只含有两个未知数;
二看整理化简后的方程是否具备两个未知数的系数都不为 0,且含未知数的项的次数都是 1.
方法
例1 已知 |m-1| x | m |+y2n-1=3 是二元一次方程,
则 m+n=_____.
解析:根据题意得 | m |=1 且 |m-1|≠0,2n-1=1,解得 m=-1,n=1,所以 m+n=0.
0
由方程是二元一次方程可知:
(1) 未知数的系数不为 0;
(2) 含未知数的项的次数都是 1.
方法
若 x2m-1 + 5y3n-2m = 7 是二元一次方程,则 m =____,n =____.
2m - 1 = 1
1
3n - 2m = 1
1
像这样,把两个含有相同未知数的二元一次方程 (或者一个二元一次方程,一个一元一次方程) 联立起来,组成的方程组,叫做二元一次方程组.
x+y = 10,
2x+y = 16.
叫做方程组
下面方程组是二元一次方程组吗?
(1) (2)
(3) (4)
是
是
不是
不是
x+y=60,
x-y=20
把x=40,y=20代入方程组
的每一个方程中,每
一个方程左、右两边的值相等吗?
40+20= 60,40-20= 20.每一个方程左、右两边的值都相等.
在一个二元一次方程组中,使每一个方程的左、右两边的值都相等的一组未知数的值,叫做这个方程组的一个解.
x+y=60,
x-y=20
把x=40,y=20代入方程组
的每一个方程中,每
一个方程左、右两边的值相等吗?
这个解通常记做
x=40,
y=20.
求方程组的解的过程叫做解方程组.
在一个二元一次方程组中,使每一个方程的左、右两边的值都相等的一组未知数的值,叫做这个方程组的一个解.
一个
一个
?
一个二元一次方程有无数多个解
1. 下列各组数是不是方程 2a = 3b + 20 的解
a = 4,
b = 3;
a = 100,
b = 60.
①
②
不是
是
左边 ≠ 右边
右边 = 3×3 + 20
右边 = 3×60 + 20
左边 = 2×100
左边 = 右边
左边 = 2×4
结论:一般地,二元一次方程有无数个解,而二元一次方程组只有一个解.
2. 二元一次方程组 的解是 ( )
{
x + 2y = 10,
y = 2x
A.{
C.{
D.{
B.{
x = 4,
y = 3
x = 3,
y = 6
x = 2,
y = 4
x = 4,
y = 2
C
小玲在文具店买了3本练习本,2支圆珠笔,共花去8元,其中购买的练习本比圆珠笔多花4元.
(1)为了知道练习本、圆珠笔的单价是多少元,你能列出相应的方程组吗
(2) 是列出的二元一次方程组的解吗?
例
x=2,
y=1
解:(1)设练习本的单价是x元,圆珠笔的单价是y元.
根据题意得:
3x+2y=8, ①
3x-2y=4. ②
(2)把 代入方程①中,左边=右边,
x=2,
y=1
把 代入方程②中,左边=右边,
x=2,
y=1
所以 是方程组 的解.
x=2,
y=1
3x+2y=8,
3x-2y=4.
1. 是上例中方程组的解吗?
解 把 代入方程①中,左边≠右边,
把 代入方程②中,左边≠右边,
所以 不是方程组 的解.
2 若 是方程 x - ky = 1 的解,则 k 的值为
.
{
x = -2,
y = 3
解析:将 代入原方程得 -2 - 3k = 1,解得
k = -1.
{
x = -2,
y = 3
-1
3 加工某种产品须经两道工序,第一道工序每人每天可完成 900 件,第二道工序每人每天可完成 1200 件.现有 7 位工人参加这两道工序,应怎样安排人力,才能使每天第一、二道工序所完成的件数相等?
解:设第一道工序安排 x 人,第二道工序安排 y 人.根据题意得
答:第一道工序安排 4 人,第二道工序安排 3 人.
解这个方程组,得
1. 二元一次方程组 的解是( ).
C
通过计算得 x=1,y=1或“特殊值法”,将A、B、C、D逐一代入方程组检验,只有C项正确,故选C.
解析
x + = 1,
y + x = 2
2. 下列不是二元一次方程组的是 ( )
A.
x + y = 3,
x - y = 1
B.
C.
D.
6x + 4y = 9,
y = 3x + 4
B
x = 1,
x + y = 1
3. 关于 x、y 的方程 ax2 + bx + 2y = 3 是一个二元一次方程,则 a、b 分别满足( )
A. a = 0 且 b = 0 B. a = 0 或 b = 0
C. a = 0 且 b≠0 D. a≠0 且 b≠0
C
4.若关于x,y的二元一次方程组 的解也是二元一次方程2x+3y=6的解,则k的值为( ).
B
解析
由 解得 代入2x+3y=6,
得 ,故选B.
5. 小刘同学用 10 元钱购买了两种不同的贺卡共 8 张, 单价分别是 1 元与 2 元.设他购买了 1 元的贺卡 x 张, 2 元的贺卡 y 张,那么可列方程组 ( )
A. B.
C. D.
D
6.一条船顺流航行,每小时行24km;逆流航行,每小时行18 km.
(1)为了求轮船在静水中的速度x与水的流速y,你能列出相应的方程组吗
解:(1)根据题意得:
x+y=24, ①
x-y=18. ②
(2) 是列出的二元一次方程组的解吗?
x=21,
y=3
(2)把 分别代入方程①②中,方程都是左边=右边,
x=21,
y=3
所以是方程组的解.
7、甲、乙两位同学在解关于的方程组
,乙看错了方程组中的,乙的解为
(1)求出正确的、 的值。
(2)求+的值。
解:(1)把 代入 ② ,得
把 代入①,得
(2)由(1)可知
8.写出方程x+2y=5 在自然数范围内的所有解.
x=1,
y=2
x=3,
y=1
x=5,
y=0
认识二元一次方程组
二元一次方程及二元一次方程组的定义
二元一次方程及二元一次方程组的解
根据实际问题列二元一次方程组
习题1.1
第3 、4 题
