第二章 对称图形 —圆 期末拔高练习(含简单答案) 2023--2024学年苏科版数学九年级上册
文档属性
| 名称 | 第二章 对称图形 —圆 期末拔高练习(含简单答案) 2023--2024学年苏科版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 582.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 12:11:12 | ||
图片预览



文档简介
苏科版(2012)数学九年级上册第二章对称图形——圆期末章节拔高练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,点在上,,若,则的度数是( )
A. B. C. D.
2.下列命题中,是真命题的是( )
A.同旁内角互补
B.对角线相等的四边形各边中点连线所得四边形是矩形
C.五边形的内角和为
D.三点确定一个圆
3.如图,路线 1 是以 AB 为直径的半圆,路线 2 是四个半圆组成的曲线,一只蚂蚁要从 A爬到 B,则沿路线 1 和沿路线 2 所走的路程( )
A.路线 1 少 B.路线 2 少 C.路线 1 和路线 2 一样 D.无法确定
4.在Rt△ABC中,两直角边AC=6cm,BC=8cm,则它的外接圆的面积为()
A.100πcm B.15πcm C.25πcm D.50πcm
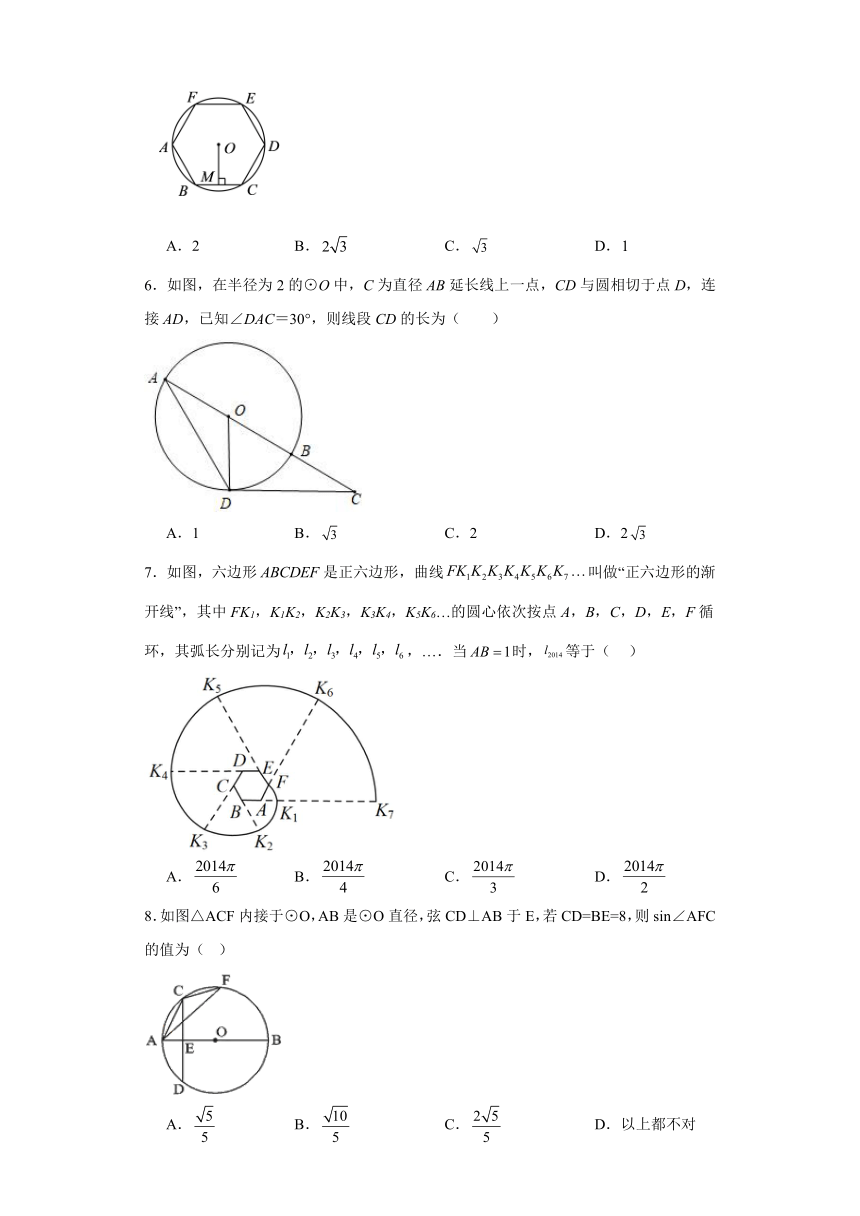
5.如图,正六边形内接于圆,半径为4,则这个正六边形的边心距为( )
A.2 B. C. D.
6.如图,在半径为2的⊙O中,C为直径AB延长线上一点,CD与圆相切于点D,连接AD,已知∠DAC=30°,则线段CD的长为( )
A.1 B. C.2 D.2
7.如图,六边形是正六边形,曲线叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为,….当时,等于( )
A. B. C. D.
8.如图△ACF内接于⊙O,AB是⊙O直径,弦CD⊥AB于E,若CD=BE=8,则sin∠AFC的值为( )
A. B. C. D.以上都不对
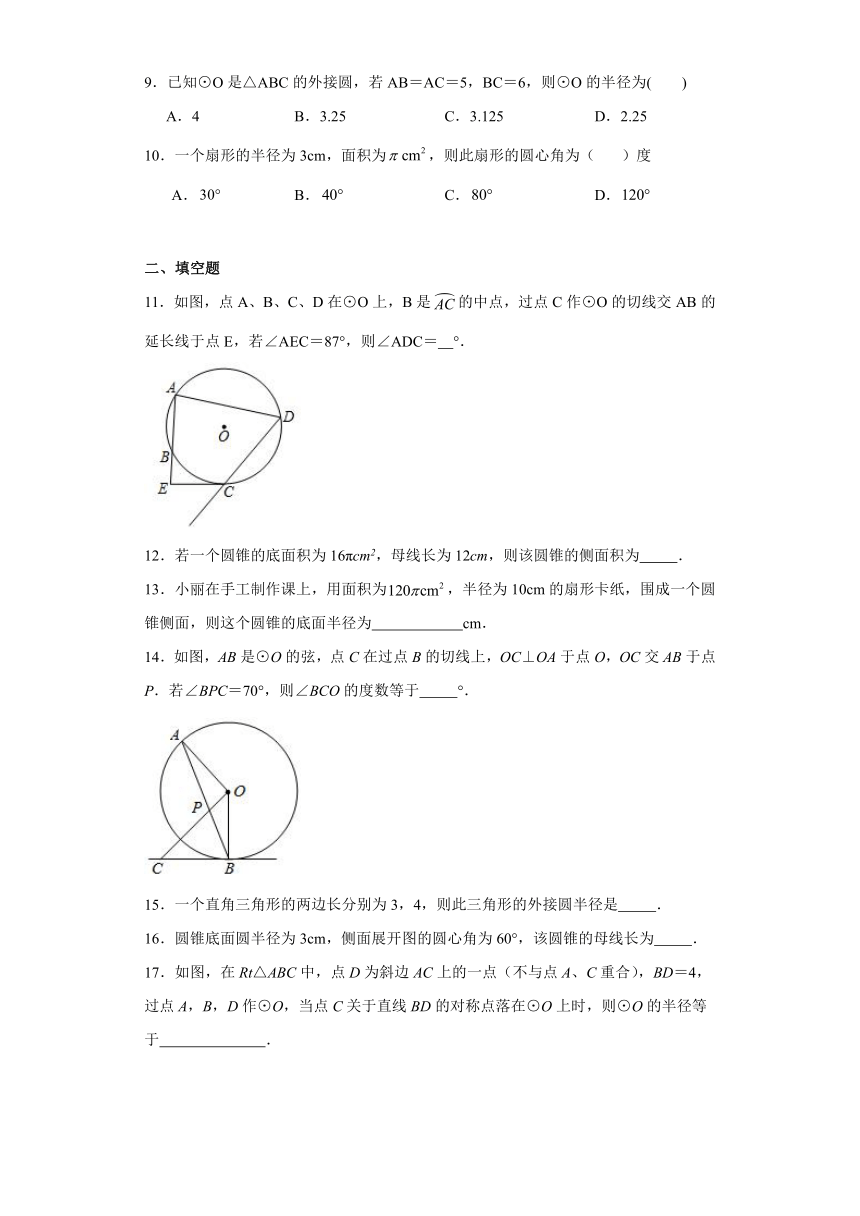
9.已知⊙O是△ABC的外接圆,若AB=AC=5,BC=6,则⊙O的半径为( )
A.4 B.3.25 C.3.125 D.2.25
10.一个扇形的半径为3cm,面积为,则此扇形的圆心角为( )度
A. B. C. D.
二、填空题
11.如图,点A、B、C、D在⊙O上,B是的中点,过点C作⊙O的切线交AB的延长线于点E,若∠AEC=87°,则∠ADC= °.
12.若一个圆锥的底面积为16πcm2,母线长为12cm,则该圆锥的侧面积为 .
13.小丽在手工制作课上,用面积为,半径为10cm的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为 cm.
14.如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA于点O,OC交AB于点P.若∠BPC=70°,则∠BCO的度数等于 °.
15.一个直角三角形的两边长分别为3,4,则此三角形的外接圆半径是 .
16.圆锥底面圆半径为3cm,侧面展开图的圆心角为60°,该圆锥的母线长为 .
17.如图,在Rt△ABC中,点D为斜边AC上的一点(不与点A、C重合),BD=4,过点A,B,D作⊙O,当点C关于直线BD的对称点落在⊙O上时,则⊙O的半径等于 .
18.如图,⊙O是△ABC的外接圆,∠A=45°,BC=2,则⊙O的直径为 .
19.小圆的直径等于大圆的半径,则大圆周长是小圆周长的 倍,大圆面积是小圆面积的 倍.
20.如图,正方形的边长为,点是边的中点,点是边上一动点,连接,将沿翻折得到,连接,当最小时,的长是 .
三、解答题
21.如图,在足球比赛中,甲带球奔向对方球门,当他带球冲到点A时,同伴乙已经冲到点B,此时甲是直接射门好,还是将球传给乙,让乙射门好?(仅从射门角度大小考虑)
22.【生活问题】2022年卡塔尔世界杯比赛中,某球员P带球沿直线接近球门,他在哪里射门时射门角度最大?
【操作感知】小米和小勒在研究球员P对球门的张角时,在上取一点Q,过A、B、Q三点作圆,发现直线与该圆相交或相切.如果直线与该圆相交,如图1,那么球员P由M向N的运动过程中,的大小______:(填序号)
①逐渐变大;②逐渐变小;③先变大后变小;④先变小后变大
【猜想验证】小米和小勒进一步探究发现,如果直线与该圆相切于点Q,那么球员P运动到切点Q时最大,如图2,试证明他们的发现.
【实际应用】如图3,某球员P沿垂直于方向的路线带球,请用尺规作图在上找出球员P的位置,使最大.(不写作法,保留作图痕迹)
23.如图1,在矩形中,,,点P以的速度从点A向点B运动,点Q以的速度从点C向点B运动.点P、Q同时出发,运动时间为t秒,是的外接圆.
(1)当时,的半径是______ ,与直线的位置关系是______;
(2)在点P从点A向点B运动过程中,当与矩形的边相切时,求t的值.
(3)连接,交于点N,如图2,当时,t的值是______.
24.已知为的直径,为上一点,为的中点,与相交于点.
(1)如图①,的平分线交于点,求的大小;
(2)如图②,的延长线与过点的的切线相交于点;若,求的大小.
25.如图.的直径垂直于弦,垂足是E,,求的长.
26.如图,是的直径,点,都在圆上且在的两侧,连接,,过点作, 交延长线于点, 且平分
(1)判断直线与的位置关系,并说明理由;
(2)若,,求线段的长
27. 如图,在Rt△ABC中,∠C=90°,点O在边BC上,以点O为圆心,OB为半径的圆经过点A,过点A作直线AD,使∠CAD=2∠B.
(1)判断直线AD与⊙O的位置关系,并说明理由;
(2)若OB=4,∠CAD=60°,请直接写出图中弦AB与围成的阴影部分的面积.
参考答案:
1.A
2.C
3.C
4.C
5.B
6.D
7.C
8.A
9.C
10.B
11.62
12.48πcm2
13.12
14.40
15.2或
16.18cm/18厘米
17.2
18.2
19. 2 4
20./
21.甲将球传给乙,让乙射门好
22.操作感知:③;猜想验证:略;实际应用:略
23.(1);相离
(2)或
(3)
24.(1)
(2)
25.
26.(1)相切,(2)
27.(1)直线AD与⊙O的位置关系是相切;(2)-4
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,点在上,,若,则的度数是( )
A. B. C. D.
2.下列命题中,是真命题的是( )
A.同旁内角互补
B.对角线相等的四边形各边中点连线所得四边形是矩形
C.五边形的内角和为
D.三点确定一个圆
3.如图,路线 1 是以 AB 为直径的半圆,路线 2 是四个半圆组成的曲线,一只蚂蚁要从 A爬到 B,则沿路线 1 和沿路线 2 所走的路程( )
A.路线 1 少 B.路线 2 少 C.路线 1 和路线 2 一样 D.无法确定
4.在Rt△ABC中,两直角边AC=6cm,BC=8cm,则它的外接圆的面积为()
A.100πcm B.15πcm C.25πcm D.50πcm
5.如图,正六边形内接于圆,半径为4,则这个正六边形的边心距为( )
A.2 B. C. D.
6.如图,在半径为2的⊙O中,C为直径AB延长线上一点,CD与圆相切于点D,连接AD,已知∠DAC=30°,则线段CD的长为( )
A.1 B. C.2 D.2
7.如图,六边形是正六边形,曲线叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为,….当时,等于( )
A. B. C. D.
8.如图△ACF内接于⊙O,AB是⊙O直径,弦CD⊥AB于E,若CD=BE=8,则sin∠AFC的值为( )
A. B. C. D.以上都不对
9.已知⊙O是△ABC的外接圆,若AB=AC=5,BC=6,则⊙O的半径为( )
A.4 B.3.25 C.3.125 D.2.25
10.一个扇形的半径为3cm,面积为,则此扇形的圆心角为( )度
A. B. C. D.
二、填空题
11.如图,点A、B、C、D在⊙O上,B是的中点,过点C作⊙O的切线交AB的延长线于点E,若∠AEC=87°,则∠ADC= °.
12.若一个圆锥的底面积为16πcm2,母线长为12cm,则该圆锥的侧面积为 .
13.小丽在手工制作课上,用面积为,半径为10cm的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为 cm.
14.如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA于点O,OC交AB于点P.若∠BPC=70°,则∠BCO的度数等于 °.
15.一个直角三角形的两边长分别为3,4,则此三角形的外接圆半径是 .
16.圆锥底面圆半径为3cm,侧面展开图的圆心角为60°,该圆锥的母线长为 .
17.如图,在Rt△ABC中,点D为斜边AC上的一点(不与点A、C重合),BD=4,过点A,B,D作⊙O,当点C关于直线BD的对称点落在⊙O上时,则⊙O的半径等于 .
18.如图,⊙O是△ABC的外接圆,∠A=45°,BC=2,则⊙O的直径为 .
19.小圆的直径等于大圆的半径,则大圆周长是小圆周长的 倍,大圆面积是小圆面积的 倍.
20.如图,正方形的边长为,点是边的中点,点是边上一动点,连接,将沿翻折得到,连接,当最小时,的长是 .
三、解答题
21.如图,在足球比赛中,甲带球奔向对方球门,当他带球冲到点A时,同伴乙已经冲到点B,此时甲是直接射门好,还是将球传给乙,让乙射门好?(仅从射门角度大小考虑)
22.【生活问题】2022年卡塔尔世界杯比赛中,某球员P带球沿直线接近球门,他在哪里射门时射门角度最大?
【操作感知】小米和小勒在研究球员P对球门的张角时,在上取一点Q,过A、B、Q三点作圆,发现直线与该圆相交或相切.如果直线与该圆相交,如图1,那么球员P由M向N的运动过程中,的大小______:(填序号)
①逐渐变大;②逐渐变小;③先变大后变小;④先变小后变大
【猜想验证】小米和小勒进一步探究发现,如果直线与该圆相切于点Q,那么球员P运动到切点Q时最大,如图2,试证明他们的发现.
【实际应用】如图3,某球员P沿垂直于方向的路线带球,请用尺规作图在上找出球员P的位置,使最大.(不写作法,保留作图痕迹)
23.如图1,在矩形中,,,点P以的速度从点A向点B运动,点Q以的速度从点C向点B运动.点P、Q同时出发,运动时间为t秒,是的外接圆.
(1)当时,的半径是______ ,与直线的位置关系是______;
(2)在点P从点A向点B运动过程中,当与矩形的边相切时,求t的值.
(3)连接,交于点N,如图2,当时,t的值是______.
24.已知为的直径,为上一点,为的中点,与相交于点.
(1)如图①,的平分线交于点,求的大小;
(2)如图②,的延长线与过点的的切线相交于点;若,求的大小.
25.如图.的直径垂直于弦,垂足是E,,求的长.
26.如图,是的直径,点,都在圆上且在的两侧,连接,,过点作, 交延长线于点, 且平分
(1)判断直线与的位置关系,并说明理由;
(2)若,,求线段的长
27. 如图,在Rt△ABC中,∠C=90°,点O在边BC上,以点O为圆心,OB为半径的圆经过点A,过点A作直线AD,使∠CAD=2∠B.
(1)判断直线AD与⊙O的位置关系,并说明理由;
(2)若OB=4,∠CAD=60°,请直接写出图中弦AB与围成的阴影部分的面积.
参考答案:
1.A
2.C
3.C
4.C
5.B
6.D
7.C
8.A
9.C
10.B
11.62
12.48πcm2
13.12
14.40
15.2或
16.18cm/18厘米
17.2
18.2
19. 2 4
20./
21.甲将球传给乙,让乙射门好
22.操作感知:③;猜想验证:略;实际应用:略
23.(1);相离
(2)或
(3)
24.(1)
(2)
25.
26.(1)相切,(2)
27.(1)直线AD与⊙O的位置关系是相切;(2)-4
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
