浙江省宁波市海曙区2023-2024学年九年级上学期数学期末模拟卷(含答案)
文档属性
| 名称 | 浙江省宁波市海曙区2023-2024学年九年级上学期数学期末模拟卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 220.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 12:41:30 | ||
图片预览



文档简介
2023-2024年宁波市海曙区数学九年级上学期期末模拟卷
考试范围:九年级上册全书、下册第一章
姓名: 学号: 考号: 成绩: i
一、选择题(本大题有10个小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的)
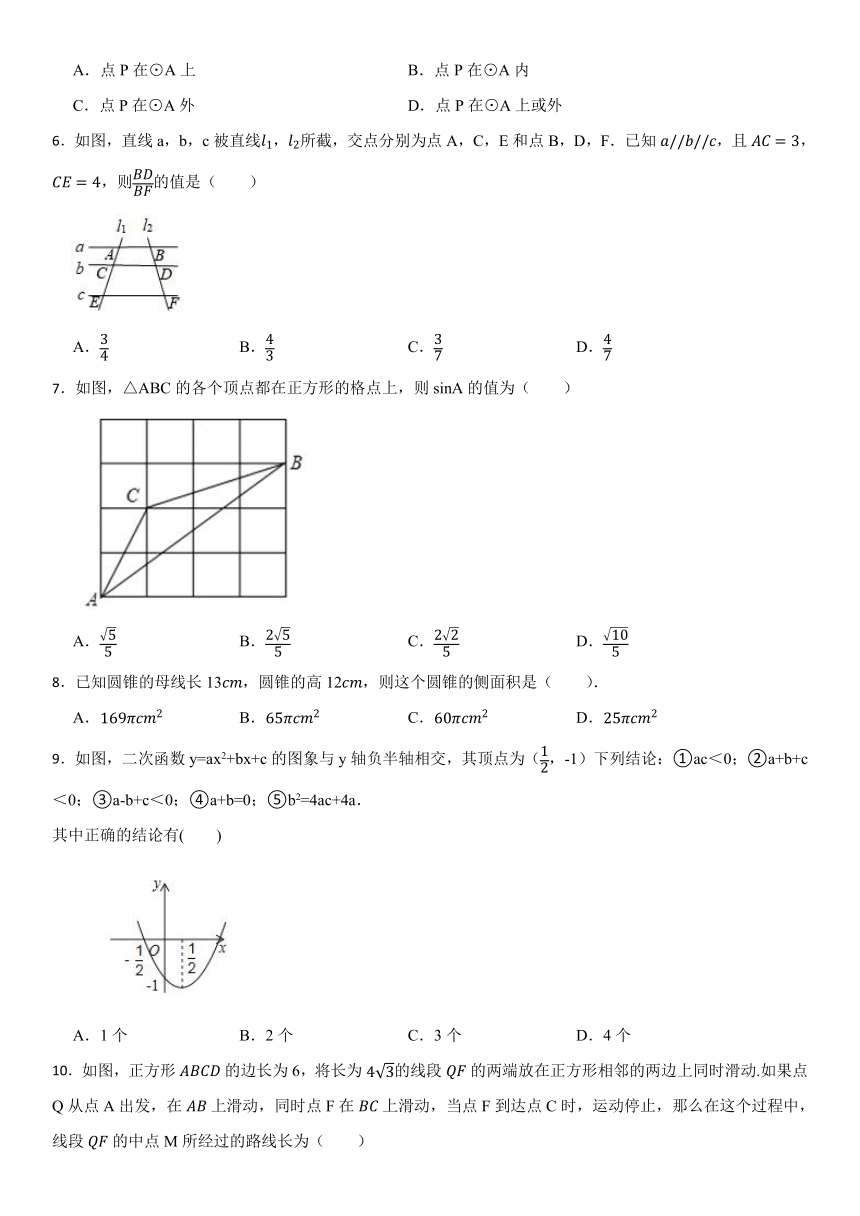
1.抛物线 的顶点坐标是( )
A.(3,1) B.(3,﹣1)
C.(﹣3,1) D.(﹣3,﹣1)
2.如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是( )
A. B.
C. D.
3.下列判断正确的是( )
A.“打开电视机,正在播NBA篮球赛”是必然事件
B.“掷一枚硬币正面朝上的概率是”表示每抛掷硬币2次就必有1次反面朝上
C.一组数据2,3,4,5,5,6的众数和中位数都是5
D.甲组数据的方差S2甲=0.24,乙组数据的方差S2乙=0.03,则乙组数据比甲组数据稳定
4.如图,AB为的直径,,,劣弧BC的长是劣弧BD长的2倍,则AC的长为( )
A. B. C.3 D.
5.⊙A半径为5,圆心A的坐标为(1,0),点P的坐标为(﹣2,4),则点P与⊙A的位置关系是( )
A.点P在⊙A上 B.点P在⊙A内
C.点P在⊙A外 D.点P在⊙A上或外
6.如图,直线a,b,c被直线,所截,交点分别为点A,C,E和点B,D,F.已知,且,,则的值是( )
A. B. C. D.
7.如图,△ABC的各个顶点都在正方形的格点上,则sinA的值为( )
A. B. C. D.
8.已知圆锥的母线长13,圆锥的高12,则这个圆锥的侧面积是( ).
A. B. C. D.
9.如图,二次函数y=ax2+bx+c的图象与y轴负半轴相交,其顶点为(,-1)下列结论:①ac<0;②a+b+c<0;③a-b+c<0;④a+b=0;⑤b2=4ac+4a.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形的边长为6,将长为的线段的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在上滑动,同时点F在上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段的中点M所经过的路线长为( )
A. B. C. D.
二、填空题(本大题有6个小题,每小题5分,共30分)
11.已知4a=3b,则 = .
12.若抛物线与x轴的两个交点分别为点A和点B,则线段AB的长为 .
13.如图,四边形为圆内接四边形,若,则 .
14.一个暗箱中放有除颜色外其他完全相同的n个红球,18个黄球,9个白球,现将球搅匀后,任意摸出1个球记下颜色,再放回暗箱,通过大量重复试验后发现,摸到黄球的频率稳定在30%附近,由此可以估算的n值是 .
15.如图,在平面直角坐标系中,以原点O为位似中心,将△OAB放大后得到△OCD,若,,则△OAB与△OCD的面积比为 .
16.如图,⊙O是△ABC的外接圆,直径AD=10,∠ABC=∠DAC,则AC长为 .
三、解答题(本大题有8小题,共80分,解答应写出文字说明、证明过程或演算步骤)
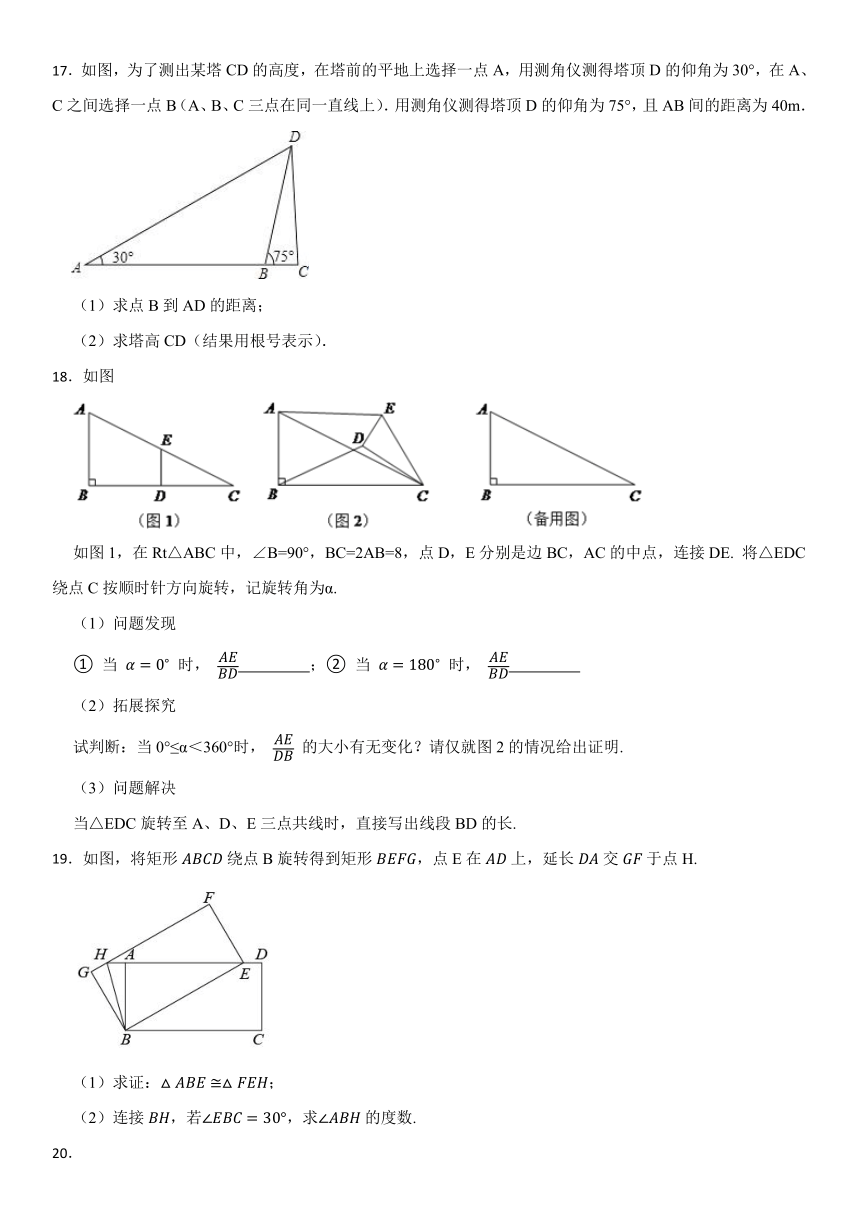
17.如图,为了测出某塔CD的高度,在塔前的平地上选择一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.
(1)求点B到AD的距离;
(2)求塔高CD(结果用根号表示).
18.如图
如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
① 当 时, ;② 当 时,
(2)拓展探究
试判断:当0°≤α<360°时, 的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
19.如图,将矩形绕点B旋转得到矩形,点E在上,延长交于点H.
(1)求证:;
(2)连接,若,求的度数.
20.
(1)解方程:;
(2)计算:.
21.在金沙县第四中学举办的第一届田径运动会中,我校的“体育达人”龙浩在“跳远”、“100米”、“200米”、“400米”四个项目中成绩都非常出色.
(1)龙浩同学如果任选一项参赛,选准“跳远”的概率为多少?
(2)运动会主委会规定最多只能参加两项,用画树状图或列表的方法,求龙浩同学选准“跳远”和“100米”的概率.
22.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=10,∠CBD=36°,求的长.
23. 如图,已知正比例函数的图象与抛物线相交于点.
(1)求与的值;
(2)若点在函数的图象上,抛物线的顶点是,求的面积;
(3)若点是轴上一个动点,求当最小时点的坐标.
24.如图,在矩形ABCD中,AB:BC=3:2,点F、G分别在边AB、CD上,将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形EFGP,EP交CD于点H,连接AE交GF于点O.
(1)若BC=8,E是BC中点,求BF的长;
(2)试探究GF与AE之间的位置关系与数量关系,并说明理由;
(3)连接CP,若 ,GF=2 ,求线段BE和CP的长..
2023-2024宁波市海曙区数学九年级上学期期末模拟卷参考答案
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】A
6.【答案】C
7.【答案】A
8.【答案】B
9.【答案】D
10.【答案】B
11.【答案】
12.【答案】4
13.【答案】120°
14.【答案】33
15.【答案】1:9
16.【答案】
17.【答案】(1)解:过点B作BE⊥AD于点E,
∵AB=40m,∠A=30°,
∴BE= AB=20m,AE= =20 m,
即点B到AD的距离为20m
(2)解:在Rt△ABE中,∵∠A=30°,∴∠ABE=60°,∵∠DBC=75°,∴∠EBD=180°﹣60°﹣75°=45°,
∴DE=EB=20m,
则AD=AE+EB=20 +20=20( +1)(m),在Rt△ADC中,∠A=30°,∴DC= =(10+10 )m.答:塔高CD为(10+10 )m.
18.【答案】(1);
(2)解:如图2,
,
当0°≤α<360°时, 的大小没有变化,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵ ,
∴△ECA∽△DCB,
∴
(3)解:①如图3,
,
∵AC=4 ,CD=4,CD⊥AD,
∴AD=
∵AD=BC,AB=DC,∠B=90°,
∴四边形ABCD是矩形,
∴BD=AC= .
②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,
,
∵AC= ,CD=4,CD⊥AD,
∴AD= ,
∵点D、E分别是边BC、AC的中点,
∴DE= =2,
∴AE=AD-DE=8-2=6,
由(2),可得
,
∴BD= .
综上所述,BD的长为 或
19.【答案】(1)证明:
∵四边形是矩形,
∴,,
由旋转性质,得:,,
∴,,
∵在矩形中,,
∴,
在和中,
,
∴,
(2)解:∵四边形是矩形,
∴,
∴,
∵,
∴,
∴,
∵,
∴,即的度数为.
20.【答案】(1)解:,
∴,
∴,
∴
(2)解:
21.【答案】(1)解:龙浩抽到四个项目的机会均等,∴选准“跳远”的概率为.
(2)解:列表如下:
第一次 第二次 跳远 100米 200米 400米
跳远 (跳、100) (跳、200) (跳、400)
100米 (100、跳) (100、200) (100、400)
200米 (200、跳) (200、100) (200、400)
400米 (400、跳) (400、100) (400、200)
总共有12种结果,每种结果出现的可能性相同,而选准“跳远”和“100米”比赛的有两种情况,
∴.
22.【答案】(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,
即OC⊥AD,
∴AE=ED.
(2)解:∵OC⊥AD,
∴,
∴∠ABC=∠CBD=36°,
∴∠AOC=2∠ABC=2×36°=72°,
∴的长==2π
23.【答案】(1)解:点在函数的图象上,
,
点在抛物线上,
,
解得,;
(2)解:
点在函数的图象上,
,得,
点,
抛物线的顶点是,
点,
点的坐标为,
的面积是:.
(3)解:设点关于轴的对称点为,
则的坐标为,
连接交轴于点,此时最小,
设直线的解析式是,把,的坐标代入,
得 ,
解得,
,当时,.
点的坐标是.
24.【答案】(1)解:∵AB:BC=3:2,BC=8,E是BC中点,
∴AB=12,BE=4,
设BF的长为x,则AF=12﹣x,
由矩形ABCD沿GF折叠,使点A落在BC边上的点E处得EF=AF=12﹣x,
在Rt△BEF中,BE2+BF2=EF2,
∴42+x2=(12﹣x)2,解得x= ,
∴BF的长为 ;
(2)解:GF与AE之间的位置关系是:GF⊥AE,GF与AE之间的数量关系是: = ,理由如下:
∵矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形EFGP,
∴A、E关于FG对称,
∴GF⊥AE,
过点G作GM⊥AB于M,如图:
∵AE⊥GF,
∴∠AOF=∠GMF=∠ABE=90°,
∴∠BAE+∠AFO=90°,∠AFO+∠FGM=90°,
∴∠BAE=∠FGM,
∴△ABE∽△GMF,
∴ = ,
∵∠AMG=∠D=∠DAM=90°,
∴四边形AMGD是矩形,
∴GM=AD,
∴ = = = ;
(3)解:过点P作PN⊥BC交BC的延长线于N,如图:
由 ,设BE=3k,则BF=4k,EF=AF=5k,AB=9k,
∵ = ,FG=2 ,
∴AE=3 ,
∴(3k)2+(9k)2=(3 )2,
∴k=1或﹣1(舍弃),
∴BE=3,AB=9,
∵BC:AB=2:3,
∴BC=6,
∴BE=CE=3,AD=PE=BC=6,
∵∠EBF=∠FEP=∠PME=90°,
∴∠FEB+∠PEN=90°,∠PEN+∠EPN=90°,
∴∠FEB=∠EPN,
∴△FBE∽△ENP,
∴ = = = ,
∴ = = ,
∴EN= ,PN= ,
∴CN=EN﹣EC= ﹣3= ,
∴CP= = ,
∴线段BE的长是3,CP的长是 .
考试范围:九年级上册全书、下册第一章
姓名: 学号: 考号: 成绩: i
一、选择题(本大题有10个小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.抛物线 的顶点坐标是( )
A.(3,1) B.(3,﹣1)
C.(﹣3,1) D.(﹣3,﹣1)
2.如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是( )
A. B.
C. D.
3.下列判断正确的是( )
A.“打开电视机,正在播NBA篮球赛”是必然事件
B.“掷一枚硬币正面朝上的概率是”表示每抛掷硬币2次就必有1次反面朝上
C.一组数据2,3,4,5,5,6的众数和中位数都是5
D.甲组数据的方差S2甲=0.24,乙组数据的方差S2乙=0.03,则乙组数据比甲组数据稳定
4.如图,AB为的直径,,,劣弧BC的长是劣弧BD长的2倍,则AC的长为( )
A. B. C.3 D.
5.⊙A半径为5,圆心A的坐标为(1,0),点P的坐标为(﹣2,4),则点P与⊙A的位置关系是( )
A.点P在⊙A上 B.点P在⊙A内
C.点P在⊙A外 D.点P在⊙A上或外
6.如图,直线a,b,c被直线,所截,交点分别为点A,C,E和点B,D,F.已知,且,,则的值是( )
A. B. C. D.
7.如图,△ABC的各个顶点都在正方形的格点上,则sinA的值为( )
A. B. C. D.
8.已知圆锥的母线长13,圆锥的高12,则这个圆锥的侧面积是( ).
A. B. C. D.
9.如图,二次函数y=ax2+bx+c的图象与y轴负半轴相交,其顶点为(,-1)下列结论:①ac<0;②a+b+c<0;③a-b+c<0;④a+b=0;⑤b2=4ac+4a.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形的边长为6,将长为的线段的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在上滑动,同时点F在上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段的中点M所经过的路线长为( )
A. B. C. D.
二、填空题(本大题有6个小题,每小题5分,共30分)
11.已知4a=3b,则 = .
12.若抛物线与x轴的两个交点分别为点A和点B,则线段AB的长为 .
13.如图,四边形为圆内接四边形,若,则 .
14.一个暗箱中放有除颜色外其他完全相同的n个红球,18个黄球,9个白球,现将球搅匀后,任意摸出1个球记下颜色,再放回暗箱,通过大量重复试验后发现,摸到黄球的频率稳定在30%附近,由此可以估算的n值是 .
15.如图,在平面直角坐标系中,以原点O为位似中心,将△OAB放大后得到△OCD,若,,则△OAB与△OCD的面积比为 .
16.如图,⊙O是△ABC的外接圆,直径AD=10,∠ABC=∠DAC,则AC长为 .
三、解答题(本大题有8小题,共80分,解答应写出文字说明、证明过程或演算步骤)
17.如图,为了测出某塔CD的高度,在塔前的平地上选择一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.
(1)求点B到AD的距离;
(2)求塔高CD(结果用根号表示).
18.如图
如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
① 当 时, ;② 当 时,
(2)拓展探究
试判断:当0°≤α<360°时, 的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
19.如图,将矩形绕点B旋转得到矩形,点E在上,延长交于点H.
(1)求证:;
(2)连接,若,求的度数.
20.
(1)解方程:;
(2)计算:.
21.在金沙县第四中学举办的第一届田径运动会中,我校的“体育达人”龙浩在“跳远”、“100米”、“200米”、“400米”四个项目中成绩都非常出色.
(1)龙浩同学如果任选一项参赛,选准“跳远”的概率为多少?
(2)运动会主委会规定最多只能参加两项,用画树状图或列表的方法,求龙浩同学选准“跳远”和“100米”的概率.
22.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=10,∠CBD=36°,求的长.
23. 如图,已知正比例函数的图象与抛物线相交于点.
(1)求与的值;
(2)若点在函数的图象上,抛物线的顶点是,求的面积;
(3)若点是轴上一个动点,求当最小时点的坐标.
24.如图,在矩形ABCD中,AB:BC=3:2,点F、G分别在边AB、CD上,将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形EFGP,EP交CD于点H,连接AE交GF于点O.
(1)若BC=8,E是BC中点,求BF的长;
(2)试探究GF与AE之间的位置关系与数量关系,并说明理由;
(3)连接CP,若 ,GF=2 ,求线段BE和CP的长..
2023-2024宁波市海曙区数学九年级上学期期末模拟卷参考答案
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】A
6.【答案】C
7.【答案】A
8.【答案】B
9.【答案】D
10.【答案】B
11.【答案】
12.【答案】4
13.【答案】120°
14.【答案】33
15.【答案】1:9
16.【答案】
17.【答案】(1)解:过点B作BE⊥AD于点E,
∵AB=40m,∠A=30°,
∴BE= AB=20m,AE= =20 m,
即点B到AD的距离为20m
(2)解:在Rt△ABE中,∵∠A=30°,∴∠ABE=60°,∵∠DBC=75°,∴∠EBD=180°﹣60°﹣75°=45°,
∴DE=EB=20m,
则AD=AE+EB=20 +20=20( +1)(m),在Rt△ADC中,∠A=30°,∴DC= =(10+10 )m.答:塔高CD为(10+10 )m.
18.【答案】(1);
(2)解:如图2,
,
当0°≤α<360°时, 的大小没有变化,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵ ,
∴△ECA∽△DCB,
∴
(3)解:①如图3,
,
∵AC=4 ,CD=4,CD⊥AD,
∴AD=
∵AD=BC,AB=DC,∠B=90°,
∴四边形ABCD是矩形,
∴BD=AC= .
②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,
,
∵AC= ,CD=4,CD⊥AD,
∴AD= ,
∵点D、E分别是边BC、AC的中点,
∴DE= =2,
∴AE=AD-DE=8-2=6,
由(2),可得
,
∴BD= .
综上所述,BD的长为 或
19.【答案】(1)证明:
∵四边形是矩形,
∴,,
由旋转性质,得:,,
∴,,
∵在矩形中,,
∴,
在和中,
,
∴,
(2)解:∵四边形是矩形,
∴,
∴,
∵,
∴,
∴,
∵,
∴,即的度数为.
20.【答案】(1)解:,
∴,
∴,
∴
(2)解:
21.【答案】(1)解:龙浩抽到四个项目的机会均等,∴选准“跳远”的概率为.
(2)解:列表如下:
第一次 第二次 跳远 100米 200米 400米
跳远 (跳、100) (跳、200) (跳、400)
100米 (100、跳) (100、200) (100、400)
200米 (200、跳) (200、100) (200、400)
400米 (400、跳) (400、100) (400、200)
总共有12种结果,每种结果出现的可能性相同,而选准“跳远”和“100米”比赛的有两种情况,
∴.
22.【答案】(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,
即OC⊥AD,
∴AE=ED.
(2)解:∵OC⊥AD,
∴,
∴∠ABC=∠CBD=36°,
∴∠AOC=2∠ABC=2×36°=72°,
∴的长==2π
23.【答案】(1)解:点在函数的图象上,
,
点在抛物线上,
,
解得,;
(2)解:
点在函数的图象上,
,得,
点,
抛物线的顶点是,
点,
点的坐标为,
的面积是:.
(3)解:设点关于轴的对称点为,
则的坐标为,
连接交轴于点,此时最小,
设直线的解析式是,把,的坐标代入,
得 ,
解得,
,当时,.
点的坐标是.
24.【答案】(1)解:∵AB:BC=3:2,BC=8,E是BC中点,
∴AB=12,BE=4,
设BF的长为x,则AF=12﹣x,
由矩形ABCD沿GF折叠,使点A落在BC边上的点E处得EF=AF=12﹣x,
在Rt△BEF中,BE2+BF2=EF2,
∴42+x2=(12﹣x)2,解得x= ,
∴BF的长为 ;
(2)解:GF与AE之间的位置关系是:GF⊥AE,GF与AE之间的数量关系是: = ,理由如下:
∵矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形EFGP,
∴A、E关于FG对称,
∴GF⊥AE,
过点G作GM⊥AB于M,如图:
∵AE⊥GF,
∴∠AOF=∠GMF=∠ABE=90°,
∴∠BAE+∠AFO=90°,∠AFO+∠FGM=90°,
∴∠BAE=∠FGM,
∴△ABE∽△GMF,
∴ = ,
∵∠AMG=∠D=∠DAM=90°,
∴四边形AMGD是矩形,
∴GM=AD,
∴ = = = ;
(3)解:过点P作PN⊥BC交BC的延长线于N,如图:
由 ,设BE=3k,则BF=4k,EF=AF=5k,AB=9k,
∵ = ,FG=2 ,
∴AE=3 ,
∴(3k)2+(9k)2=(3 )2,
∴k=1或﹣1(舍弃),
∴BE=3,AB=9,
∵BC:AB=2:3,
∴BC=6,
∴BE=CE=3,AD=PE=BC=6,
∵∠EBF=∠FEP=∠PME=90°,
∴∠FEB+∠PEN=90°,∠PEN+∠EPN=90°,
∴∠FEB=∠EPN,
∴△FBE∽△ENP,
∴ = = = ,
∴ = = ,
∴EN= ,PN= ,
∴CN=EN﹣EC= ﹣3= ,
∴CP= = ,
∴线段BE的长是3,CP的长是 .
同课章节目录
