九年级上册数学湘教版(新)第4章锐角三角函数小结与复习教案
文档属性
| 名称 | 九年级上册数学湘教版(新)第4章锐角三角函数小结与复习教案 | 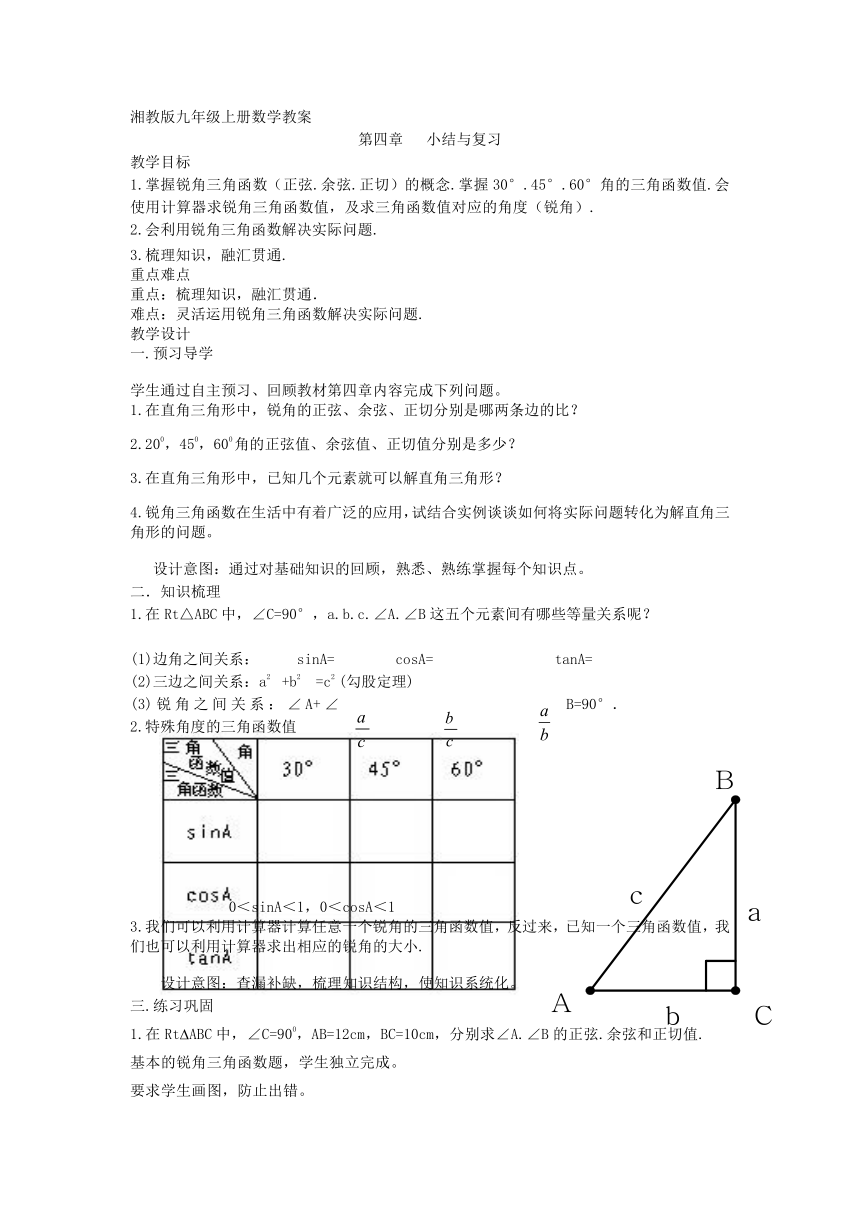 | |
| 格式 | zip | ||
| 文件大小 | 42.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-19 10:00:02 | ||
图片预览

文档简介
湘教版九年级上册数学教案
第四章 小结与复习
教学目标
1.掌握锐角三角函数(正弦.余 ( http: / / www.21cnjy.com )弦.正切)的概念.掌握30°.45°.60°角的三角函数值.会使用计算器求锐角三角函数值,及求三角函数值对应的角度(锐角).
2.会利用锐角三角函数解决实际问题.
梳理知识,融汇贯通.
重点难点
重点:梳理知识,融汇贯通.
难点:灵活运用锐角三角函数解决实际问题.
教学设计
一.预习导学
学生通过自主预习、回顾教材第四章内容完成下列问题。
在直角三角形中,锐角的正弦、余弦、正切分别是哪两条边的比?
200,450,600角的正弦值、余弦值、正切值分别是多少?
在直角三角形中,已知几个元素就可以解直角三角形?
锐角三角函数在生活中有着广泛的应用,试结合实例谈谈如何将实际问题转化为解直角三角形的问题。
设计意图:通过对基础知识的回顾,熟悉、熟练掌握每个知识点。
二.知识梳理
1.在Rt△ABC中,∠C=90°,a.b.c.∠A.∠B这五个元素间有哪些等量关系呢?
(1)边角之间关系: sinA= cosA= tanA=
(2)三边之间关系:a2 +b2 =c2 (勾股定理)
(3)锐角之间关系:∠A+∠B=90°.
2.特殊角度的三角函数值
0<sinA<1,0<cosA<1
我们可以利用计算器计算任意一个锐角的三角函数值,反过来,已知一个三角函数值,我们也可以利用计算器求出相应的锐角的大小.
设计意图:查漏补缺,梳理知识结构,使知识系统化。
三.练习巩固
1.在Rt ABC中,∠C=900,AB=12cm,BC=10cm,分别求∠A.∠B的正弦.余弦和正切值.
基本的锐角三角函数题,学生独立完成。
要求学生画图,防止出错。
设计意图:检查学生锐角三角函数的熟练程度,强化学生的数形结合思想。
2.求下列各式的值
(1) ; (2);
(3) ; (4)
设计意图:这道题主要考查学生对特殊角的三角函数值是否记得牢固,运用熟练。
要求学生独立完成,然后小组核对。老师巡查,帮助后进生。
部分学生对二次根式的运算,特别是分母有理化,已经有些生疏,需要特别指导解决。
在Rt ABC中,∠C=900,∠A=300,c=12cm,求∠B,a,b.
设计意图:这是基本的解直角三角形的题,主要是便于学生巩固解直角三角形的知识。
由学生独立完成,然后小组内讨论交流,修正答案.
要求学生先画图,再解题。
4.如图所示,△ABC中,∠A=30°,AB=8 ,AC= 6 ,求△ABC的面积S及A到BC边的距离d.
此题由小组合作完成,然后小组派代表上台展示.
要求面积,先作高.过点B作BD⊥AC于D点.
在Rt ABD中,根据锐角三角函数可以求得BD=4,AD=
△ABC的面积S=
CD=AC-AD= 在Rt BCD中,根据勾股定理可求得BC=
由△ABC的面积S=,可以求得d的值.
四.拓展提升
在锐角 ABC中,∠A,∠B,∠C的对边分别为a,b,c
(1) ABC的面积S与∠A,b,c之间有什么关系?
解:过点C作 ABC的高CD.
在Rt ACD中,,得出
所以,S=
求证:
证明:在Rt ACD中,,得出
同理,在Rt BCD中,可得出
所以,
从而有
教学反思
本章内容中,多数基础知识,学生还是基本能够掌握,但解直角三角形的应用,特别是坡度问题、测量问题、航海问题等,学生还是有较大的难度。
本节课的教学,一方面帮助学生梳理了本章的知 ( http: / / www.21cnjy.com )识结构,巩固了每个知识点,使知识结构化、系统化;另一方面继续渗透和强化了数形结合、方程思想等数学思想。同时拓展了本章的知识,满足了不同层次学生的需求。
第四章 小结与复习
教学目标
1.掌握锐角三角函数(正弦.余 ( http: / / www.21cnjy.com )弦.正切)的概念.掌握30°.45°.60°角的三角函数值.会使用计算器求锐角三角函数值,及求三角函数值对应的角度(锐角).
2.会利用锐角三角函数解决实际问题.
梳理知识,融汇贯通.
重点难点
重点:梳理知识,融汇贯通.
难点:灵活运用锐角三角函数解决实际问题.
教学设计
一.预习导学
学生通过自主预习、回顾教材第四章内容完成下列问题。
在直角三角形中,锐角的正弦、余弦、正切分别是哪两条边的比?
200,450,600角的正弦值、余弦值、正切值分别是多少?
在直角三角形中,已知几个元素就可以解直角三角形?
锐角三角函数在生活中有着广泛的应用,试结合实例谈谈如何将实际问题转化为解直角三角形的问题。
设计意图:通过对基础知识的回顾,熟悉、熟练掌握每个知识点。
二.知识梳理
1.在Rt△ABC中,∠C=90°,a.b.c.∠A.∠B这五个元素间有哪些等量关系呢?
(1)边角之间关系: sinA= cosA= tanA=
(2)三边之间关系:a2 +b2 =c2 (勾股定理)
(3)锐角之间关系:∠A+∠B=90°.
2.特殊角度的三角函数值
0<sinA<1,0<cosA<1
我们可以利用计算器计算任意一个锐角的三角函数值,反过来,已知一个三角函数值,我们也可以利用计算器求出相应的锐角的大小.
设计意图:查漏补缺,梳理知识结构,使知识系统化。
三.练习巩固
1.在Rt ABC中,∠C=900,AB=12cm,BC=10cm,分别求∠A.∠B的正弦.余弦和正切值.
基本的锐角三角函数题,学生独立完成。
要求学生画图,防止出错。
设计意图:检查学生锐角三角函数的熟练程度,强化学生的数形结合思想。
2.求下列各式的值
(1) ; (2);
(3) ; (4)
设计意图:这道题主要考查学生对特殊角的三角函数值是否记得牢固,运用熟练。
要求学生独立完成,然后小组核对。老师巡查,帮助后进生。
部分学生对二次根式的运算,特别是分母有理化,已经有些生疏,需要特别指导解决。
在Rt ABC中,∠C=900,∠A=300,c=12cm,求∠B,a,b.
设计意图:这是基本的解直角三角形的题,主要是便于学生巩固解直角三角形的知识。
由学生独立完成,然后小组内讨论交流,修正答案.
要求学生先画图,再解题。
4.如图所示,△ABC中,∠A=30°,AB=8 ,AC= 6 ,求△ABC的面积S及A到BC边的距离d.
此题由小组合作完成,然后小组派代表上台展示.
要求面积,先作高.过点B作BD⊥AC于D点.
在Rt ABD中,根据锐角三角函数可以求得BD=4,AD=
△ABC的面积S=
CD=AC-AD= 在Rt BCD中,根据勾股定理可求得BC=
由△ABC的面积S=,可以求得d的值.
四.拓展提升
在锐角 ABC中,∠A,∠B,∠C的对边分别为a,b,c
(1) ABC的面积S与∠A,b,c之间有什么关系?
解:过点C作 ABC的高CD.
在Rt ACD中,,得出
所以,S=
求证:
证明:在Rt ACD中,,得出
同理,在Rt BCD中,可得出
所以,
从而有
教学反思
本章内容中,多数基础知识,学生还是基本能够掌握,但解直角三角形的应用,特别是坡度问题、测量问题、航海问题等,学生还是有较大的难度。
本节课的教学,一方面帮助学生梳理了本章的知 ( http: / / www.21cnjy.com )识结构,巩固了每个知识点,使知识结构化、系统化;另一方面继续渗透和强化了数形结合、方程思想等数学思想。同时拓展了本章的知识,满足了不同层次学生的需求。
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
