湘教版七年级数学上册课件:1.5有理数的乘法和除法(共71张PPT)
文档属性
| 名称 | 湘教版七年级数学上册课件:1.5有理数的乘法和除法(共71张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-22 07:23:53 | ||
图片预览











文档简介
课件71张PPT。有理数的乘法和除法1.51.5.1 有理数的乘法我们已经熟悉了非负数的乘法运算,那么如何计算
(-5)×3,
3×(-5),
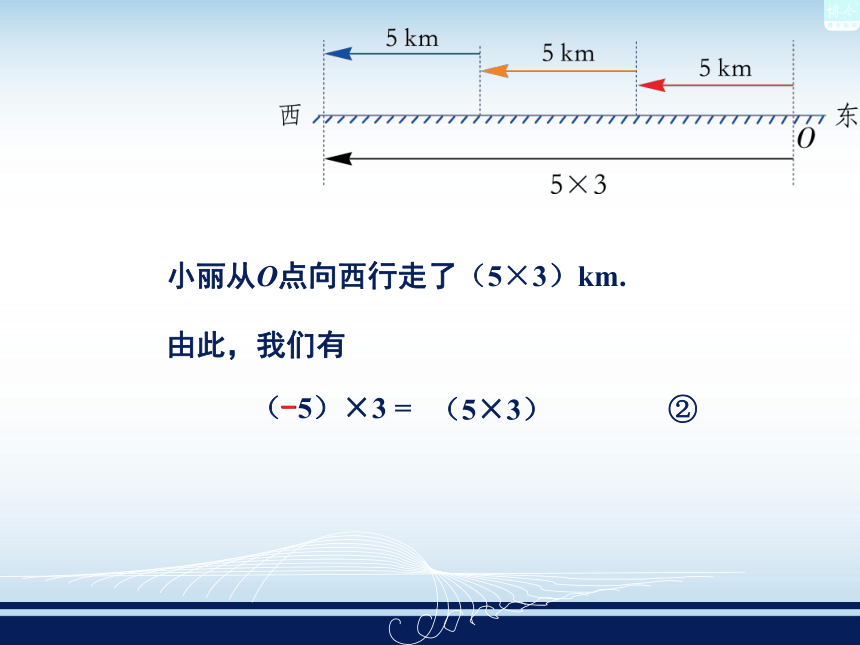
(-5)×(-3)呢? 我们把向东走的路程记为正数.如果小丽从点O出发,以5km/h的速度向西行走3h后,小丽从O点向哪个方向行走了多少千米?小丽从O点向西行走了(5×3)km.由此,我们有(-5)×3 =(5×3)②- 我们已经知道(-5)×3 = -(5×3),那么3×(-5 ),(- 5)×(-3)又应怎样计算呢? 非负数的乘法与加法是用分配律联系起来的,因此,当数扩充到有理数后,要规定有理数的乘法法则,当然也要求它满足分配律,以便把乘法与加法联系起来.如果它满足分配律,那么就会有 3×(-5)+3×5=3× [(-5)+5]=3×0=0这表明3×(-5)与3×5互为相反数,于是有3×(-5)=-(3×5). ③异号两数相乘得负数,并且把绝对值相乘.从②、③式受到启发,一般规定:(-)×(+)→(-)(+)×(-)→(-)任何数与0相乘,都得0. 类似地,我们有(-5)×(-3)+(-5)×3
=(-5)×[(-3)+3]
=(-5)×0
= 0这表明(-5)×(-3)与(-5)×3互为相反数.
因为(-5)×3= -15,而-15的相反数是15,
所以(-5)×(-3)=15 .即 (-5)×(-3)= 15 = 5×3 . ④由④式看出,(-5)×(-3)得正数,并且把绝对值5与3相乘.同号两数相乘得正数,并且把绝对值相乘.从①、④式受到启发,于是规定:(+)×(+)→(+)(-)×(-)→(+) 例1 计算:
(1)3.5 ×(-2);
(2) ;
(3) ;
(4)(-0.57)× 0.举
例解(1) 3.5 ×(-2)= -(3.5×2)根据乘法法则= -73.5)和(-2)为异号,结果为负3.5和(-2)的绝对值相乘解(2)=根据乘法法则= 为异号,结果为负它们的绝对值相乘解(3)=根据乘法法则= 1 为同号,结果为正解(4)(-0.57)× 0根据乘法法则= 0任何数与0相乘,结果为01. 填表:-14-+3-14-32. 计算:(1) ;
(2) . 在小学我们已经学过乘法的交换律、结合律,那么这两个运算律在有理数范围内是否也适用呢? 填空: (1)(-2)×4= , 4×(-2)= ;-8-8(2)[(-2)×(-3)] ×(-4)= ×(-4)= ,
(-2)×[(-3) ×(-4)]=(-2)× = .6-2412-24从上面的填空题中,你发现了什么?乘法交换律: × = × .abab即,两个有理数相乘,交换因数的位置,积不变.乘法结合律:( × )× = ×( × ).a bab cc 即,对于三个有理数相乘,可以先把前两个数相乘,再把结果与第三个数相乘;或者先把后两个数相乘,再把第一个数与所得结果相乘,积不变. 和加法类似,根据乘法交换律和乘法结合律可以推出:三个或三个以上有理数相乘,可以写成这些数的连乘式.对于连乘式,可以任意交换因数的位置,也可先把其中的几个数相乘. (1)填空:(-6)×[4+(-9)] =(-6)× = ,
(-6)×4+(-6)×(-9)= + = .-53054-2430 (2)换几个有理数试一试,你发现了什么?乘法对加法的分配律(简称为分配律):
×( + ) = × + × .b caabac (-1)a = -a利用分配律,可以得出 即,一个有理数与两个有理数的和相乘,等于把这个数分别与这两个数相乘,再把积相加. 例2 计算:
(1) ;
(2) (-12.5)×(-2.5)×(-8)× 4 .举
例解(1)=将分数逐个与60相乘= 30-20-15+12= 7分数与整数60相乘计算结果解(2) (-12.5)×(-2.5)×(-8)×4= (-12.5) ×(-8)×(-2.5)×4(-12.5)和(-8)相乘为整数= 100×(-10)(-2.5)和4相乘为整数= -1000相乘为整数的先结合起来(-12.5)和(-8)为同号相乘(-2.5)和4为异号相乘(-10)和100相乘为异号 下列各式的积是正数还是负数?积的符号与负因数(因数为负数)的个数之间有什么关系?
(1)(-2)×(-3)×(-4);
(2)(-2)×(-3)×(-4)×(-5). 几个不等于0的数相乘,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正. 例3 计算:
(1)(-8)× 4 ×(-1)×(-3) ;
(2) .举
例解(1) (-8)× 4 × (-1)×(-3)= -(8×4×1×3)将负号提出来绝对值进行相乘= -96先确定积的符号解四个负号相乘,结果为正号绝对值进行相乘= 32先确定积的符号(2)1.计算: (1)(-2)×17×(-5); (2)(-15)×3×(-4);
(3) ; (4)0.125×9×(-8);
(5)(-5)×(-4)×(-3); (6)(-1.5)×6×(-4);
(7) ; (8)(-10)× 28 × 0.1.解(1)(-2)×17×(-5)=2×5×17=170(2)(-15)×3×(-4)=15×4×3=180(3) (4)0.125×9×(-8)=-(8×0.125)×9=-9(5)(-5)×(-4)×(-3)=-(5×4×3)=-60(6)(-1.5)×6×(-4)=1.5×4×6=36(7)(8)(-10)× 28 × 0 = 02.计算: (1) ;
(2)(-4)×(-3)×(- 5)×(-2.5).
2.解(1)(2)(-4)×(-3)×(- 5)×(-2.5)
= 4×3×5×2.5
= 1501.5.2 有理数的除法我们知道 2 × 3 = 6,因此 6 ÷ 3 = 2. ①那么如何计算(-6)÷3,
6÷(-3),
(-6)÷(-3)呢? (-6)÷3=?, 6÷(-3)=?, (-6)÷(-3)=?由于 (-2)×3 = - 6 ,因此, (-6)÷3 = -2 . ②类似地,由于(-2)×(-3)= 6 ,由于 2 ×(-3) = -6 ,因此, 6÷(- 3)= -2 , ③因此, (-6)÷(-3)=2 . ④ 从这些例子受到启发,抽象出有理数的除法运算;
对于两个有理数a,b,其中b≠0,如果有一个有理数c,使得cb = a,那么规定a÷b=c,且把c叫作a除以b的商.同号两数相除得正数,异号两数相除
得负数,并且把它们的绝对值相除.
0 除以任何一个不等于0的数都得0.有理数的除法是通过乘法来规定的,因此由①至④式可以得出:(+)÷(+)→(+)(-)÷(-)→(+)(-)÷(+)→(-)(+)÷(-)→(-) 例4 计算:
(1)(-24)÷4 ;
(2)(-18)÷(-9);
(3) 10 ÷(-5).举
例解(1) (-24)÷ 4= - (24 ÷ 4)根据除法法则(-24)和4为异号相除结果为负解(2)(-18)÷ (-9)= +(18 ÷ 9)根据除法法则(-18)和(-9)为同号结果为正= -6= 2解(3) 10÷(-5)= -(10 ÷ 5)根据除法法则10和(-5)为异号相除结果为负= -2 试问:10÷(-5) 还可以怎样计算 ?我们已经知道 10÷(-5)= -2 , 所以 ⑤又 由于 ,因此,我们把 叫做-5的倒数,把-5叫做 的倒数. 一般地,如果两个数的乘积等于1,那么把其中一个数叫做另一个数的倒数,也称它们互为倒数. 0没有倒数.因此,⑤式表明10除以-5等于10乘-5的倒数.除以一个不等于零的数等于乘上这个数的倒数.一般地,有理数的除法运算可以转化为乘法运算,即也可以表示成 例5 计算:
(1) ;
(2) ;
(3) .举
例解(1)= (-12)×3根据除法法则异号相乘,结果为负解(2)=根据除法法则异号相乘,结果为负 的倒数是3= -36= -35 的倒数是解(3)= 根据除法法则同号相乘,结果为正= 的倒数是 1.计算: (1)14÷(-7); (2)(-36)÷(-3);
(3)0÷ (-0.618); (4)(-48)÷12.
1.解(1)14 ÷ (-7)= -2;(2)(-36)÷(-3)= 12 ;(4)(-48)÷12 = -4.(3) 0 ÷ (-0.618) = 0; 2.填空: (1)因为 × = 1,所以 的倒数是 ;
(2) 的倒数是 ;-3的倒数是 .-6-6 3.计算: (1) (-36)÷(-0.6) ;
(2) ;
(3) ;
(4) .
60-28 下面的算式含有乘、除两种运算,怎样进行有理数的乘、除混合运算呢?可以按从左到右的顺序依次计算.也可以先将除法转化为乘法. 例3 计算:
(1)(-56)÷(-2) ÷(-8);举
例(2)(-10)÷[(-5)×(-2)];(3)(4)解(1)(-56)÷(-2) ÷(-8)= 28 ÷(-8)可以依次计算先算前两个数异号相除,结果为负=(2)(-10)÷[(-5)×(-2)];先计算后两个= -1解= -30 ×(-3)可以依次计算先算前两位数= 90依次计算= 0.8(3)(4)解 下面是小明同学做的一道计算题,他的计算是否正确?如果不正确,说说他错在哪里. 计算器是日常生活中常用的一种现代计算工具,因此我们可以利用计算器来计算. 计算器有各种型号,型号不同,操作方法略有不同.下面我们以某种型号的计算器(图1-17)为例介绍操作方法. 图1-17 某种电子计算器的面板示意图举
例 例7 用计算器计算(精确到0.001):
-1840× 0.28÷(-375)再将结果四舍五入后就可以得到答案1.374.解 按照下列顺序按键: 不同的计算器,操作方法可能有所不同.具体操作方法应参看计算器的使用说明书. 1.计算: (1)24÷(-3)÷(-4) ; (2)(-6)÷(-2)÷3;
(3)2÷(-7)×(-4); (4) 18÷6×(-2).
1.解(1)24÷(-3)÷(-4)= -8 ÷(-4)= 2 ;(2)(-6)÷(-2)÷3 = 3÷3 = 1 ;(3)2÷(-7)×(-4) = ×(-4) = ;(4)18 ÷6×(-2) = 3×(-2)= -6 . 2.计算: (1) ;
(2) ;
(3) . 3. 用计算器计算:
1.26÷(-15 )×80.-6.72例1 计算:(-100)×(-20)-(-3). 本题中,先计算乘法,同号为正,再将减法运算转化成加法.分析 原式=100×20+3
=2000+3
=2003.解例2 计算: .有理数的除法法则
两个有理数相除,同号得正,异号得负,并把绝对值相除.
0除以任何非0的数都得0.
除以一个数等于乘以这个数的倒数,即a÷b= a · (b≠0).分析 原式=-11×(-13)×(-13)
=-11×13×13
=-1859-1859解解例3 如图,是一个简单的数值运算程序,当输入x的值为1时,则输出的数值为 . 输入x值为1,即算式为1×(-1)+3=2,所以输出为2..2结 束
(-5)×3,
3×(-5),
(-5)×(-3)呢? 我们把向东走的路程记为正数.如果小丽从点O出发,以5km/h的速度向西行走3h后,小丽从O点向哪个方向行走了多少千米?小丽从O点向西行走了(5×3)km.由此,我们有(-5)×3 =(5×3)②- 我们已经知道(-5)×3 = -(5×3),那么3×(-5 ),(- 5)×(-3)又应怎样计算呢? 非负数的乘法与加法是用分配律联系起来的,因此,当数扩充到有理数后,要规定有理数的乘法法则,当然也要求它满足分配律,以便把乘法与加法联系起来.如果它满足分配律,那么就会有 3×(-5)+3×5=3× [(-5)+5]=3×0=0这表明3×(-5)与3×5互为相反数,于是有3×(-5)=-(3×5). ③异号两数相乘得负数,并且把绝对值相乘.从②、③式受到启发,一般规定:(-)×(+)→(-)(+)×(-)→(-)任何数与0相乘,都得0. 类似地,我们有(-5)×(-3)+(-5)×3
=(-5)×[(-3)+3]
=(-5)×0
= 0这表明(-5)×(-3)与(-5)×3互为相反数.
因为(-5)×3= -15,而-15的相反数是15,
所以(-5)×(-3)=15 .即 (-5)×(-3)= 15 = 5×3 . ④由④式看出,(-5)×(-3)得正数,并且把绝对值5与3相乘.同号两数相乘得正数,并且把绝对值相乘.从①、④式受到启发,于是规定:(+)×(+)→(+)(-)×(-)→(+) 例1 计算:
(1)3.5 ×(-2);
(2) ;
(3) ;
(4)(-0.57)× 0.举
例解(1) 3.5 ×(-2)= -(3.5×2)根据乘法法则= -73.5)和(-2)为异号,结果为负3.5和(-2)的绝对值相乘解(2)=根据乘法法则= 为异号,结果为负它们的绝对值相乘解(3)=根据乘法法则= 1 为同号,结果为正解(4)(-0.57)× 0根据乘法法则= 0任何数与0相乘,结果为01. 填表:-14-+3-14-32. 计算:(1) ;
(2) . 在小学我们已经学过乘法的交换律、结合律,那么这两个运算律在有理数范围内是否也适用呢? 填空: (1)(-2)×4= , 4×(-2)= ;-8-8(2)[(-2)×(-3)] ×(-4)= ×(-4)= ,
(-2)×[(-3) ×(-4)]=(-2)× = .6-2412-24从上面的填空题中,你发现了什么?乘法交换律: × = × .abab即,两个有理数相乘,交换因数的位置,积不变.乘法结合律:( × )× = ×( × ).a bab cc 即,对于三个有理数相乘,可以先把前两个数相乘,再把结果与第三个数相乘;或者先把后两个数相乘,再把第一个数与所得结果相乘,积不变. 和加法类似,根据乘法交换律和乘法结合律可以推出:三个或三个以上有理数相乘,可以写成这些数的连乘式.对于连乘式,可以任意交换因数的位置,也可先把其中的几个数相乘. (1)填空:(-6)×[4+(-9)] =(-6)× = ,
(-6)×4+(-6)×(-9)= + = .-53054-2430 (2)换几个有理数试一试,你发现了什么?乘法对加法的分配律(简称为分配律):
×( + ) = × + × .b caabac (-1)a = -a利用分配律,可以得出 即,一个有理数与两个有理数的和相乘,等于把这个数分别与这两个数相乘,再把积相加. 例2 计算:
(1) ;
(2) (-12.5)×(-2.5)×(-8)× 4 .举
例解(1)=将分数逐个与60相乘= 30-20-15+12= 7分数与整数60相乘计算结果解(2) (-12.5)×(-2.5)×(-8)×4= (-12.5) ×(-8)×(-2.5)×4(-12.5)和(-8)相乘为整数= 100×(-10)(-2.5)和4相乘为整数= -1000相乘为整数的先结合起来(-12.5)和(-8)为同号相乘(-2.5)和4为异号相乘(-10)和100相乘为异号 下列各式的积是正数还是负数?积的符号与负因数(因数为负数)的个数之间有什么关系?
(1)(-2)×(-3)×(-4);
(2)(-2)×(-3)×(-4)×(-5). 几个不等于0的数相乘,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正. 例3 计算:
(1)(-8)× 4 ×(-1)×(-3) ;
(2) .举
例解(1) (-8)× 4 × (-1)×(-3)= -(8×4×1×3)将负号提出来绝对值进行相乘= -96先确定积的符号解四个负号相乘,结果为正号绝对值进行相乘= 32先确定积的符号(2)1.计算: (1)(-2)×17×(-5); (2)(-15)×3×(-4);
(3) ; (4)0.125×9×(-8);
(5)(-5)×(-4)×(-3); (6)(-1.5)×6×(-4);
(7) ; (8)(-10)× 28 × 0.1.解(1)(-2)×17×(-5)=2×5×17=170(2)(-15)×3×(-4)=15×4×3=180(3) (4)0.125×9×(-8)=-(8×0.125)×9=-9(5)(-5)×(-4)×(-3)=-(5×4×3)=-60(6)(-1.5)×6×(-4)=1.5×4×6=36(7)(8)(-10)× 28 × 0 = 02.计算: (1) ;
(2)(-4)×(-3)×(- 5)×(-2.5).
2.解(1)(2)(-4)×(-3)×(- 5)×(-2.5)
= 4×3×5×2.5
= 1501.5.2 有理数的除法我们知道 2 × 3 = 6,因此 6 ÷ 3 = 2. ①那么如何计算(-6)÷3,
6÷(-3),
(-6)÷(-3)呢? (-6)÷3=?, 6÷(-3)=?, (-6)÷(-3)=?由于 (-2)×3 = - 6 ,因此, (-6)÷3 = -2 . ②类似地,由于(-2)×(-3)= 6 ,由于 2 ×(-3) = -6 ,因此, 6÷(- 3)= -2 , ③因此, (-6)÷(-3)=2 . ④ 从这些例子受到启发,抽象出有理数的除法运算;
对于两个有理数a,b,其中b≠0,如果有一个有理数c,使得cb = a,那么规定a÷b=c,且把c叫作a除以b的商.同号两数相除得正数,异号两数相除
得负数,并且把它们的绝对值相除.
0 除以任何一个不等于0的数都得0.有理数的除法是通过乘法来规定的,因此由①至④式可以得出:(+)÷(+)→(+)(-)÷(-)→(+)(-)÷(+)→(-)(+)÷(-)→(-) 例4 计算:
(1)(-24)÷4 ;
(2)(-18)÷(-9);
(3) 10 ÷(-5).举
例解(1) (-24)÷ 4= - (24 ÷ 4)根据除法法则(-24)和4为异号相除结果为负解(2)(-18)÷ (-9)= +(18 ÷ 9)根据除法法则(-18)和(-9)为同号结果为正= -6= 2解(3) 10÷(-5)= -(10 ÷ 5)根据除法法则10和(-5)为异号相除结果为负= -2 试问:10÷(-5) 还可以怎样计算 ?我们已经知道 10÷(-5)= -2 , 所以 ⑤又 由于 ,因此,我们把 叫做-5的倒数,把-5叫做 的倒数. 一般地,如果两个数的乘积等于1,那么把其中一个数叫做另一个数的倒数,也称它们互为倒数. 0没有倒数.因此,⑤式表明10除以-5等于10乘-5的倒数.除以一个不等于零的数等于乘上这个数的倒数.一般地,有理数的除法运算可以转化为乘法运算,即也可以表示成 例5 计算:
(1) ;
(2) ;
(3) .举
例解(1)= (-12)×3根据除法法则异号相乘,结果为负解(2)=根据除法法则异号相乘,结果为负 的倒数是3= -36= -35 的倒数是解(3)= 根据除法法则同号相乘,结果为正= 的倒数是 1.计算: (1)14÷(-7); (2)(-36)÷(-3);
(3)0÷ (-0.618); (4)(-48)÷12.
1.解(1)14 ÷ (-7)= -2;(2)(-36)÷(-3)= 12 ;(4)(-48)÷12 = -4.(3) 0 ÷ (-0.618) = 0; 2.填空: (1)因为 × = 1,所以 的倒数是 ;
(2) 的倒数是 ;-3的倒数是 .-6-6 3.计算: (1) (-36)÷(-0.6) ;
(2) ;
(3) ;
(4) .
60-28 下面的算式含有乘、除两种运算,怎样进行有理数的乘、除混合运算呢?可以按从左到右的顺序依次计算.也可以先将除法转化为乘法. 例3 计算:
(1)(-56)÷(-2) ÷(-8);举
例(2)(-10)÷[(-5)×(-2)];(3)(4)解(1)(-56)÷(-2) ÷(-8)= 28 ÷(-8)可以依次计算先算前两个数异号相除,结果为负=(2)(-10)÷[(-5)×(-2)];先计算后两个= -1解= -30 ×(-3)可以依次计算先算前两位数= 90依次计算= 0.8(3)(4)解 下面是小明同学做的一道计算题,他的计算是否正确?如果不正确,说说他错在哪里. 计算器是日常生活中常用的一种现代计算工具,因此我们可以利用计算器来计算. 计算器有各种型号,型号不同,操作方法略有不同.下面我们以某种型号的计算器(图1-17)为例介绍操作方法. 图1-17 某种电子计算器的面板示意图举
例 例7 用计算器计算(精确到0.001):
-1840× 0.28÷(-375)再将结果四舍五入后就可以得到答案1.374.解 按照下列顺序按键: 不同的计算器,操作方法可能有所不同.具体操作方法应参看计算器的使用说明书. 1.计算: (1)24÷(-3)÷(-4) ; (2)(-6)÷(-2)÷3;
(3)2÷(-7)×(-4); (4) 18÷6×(-2).
1.解(1)24÷(-3)÷(-4)= -8 ÷(-4)= 2 ;(2)(-6)÷(-2)÷3 = 3÷3 = 1 ;(3)2÷(-7)×(-4) = ×(-4) = ;(4)18 ÷6×(-2) = 3×(-2)= -6 . 2.计算: (1) ;
(2) ;
(3) . 3. 用计算器计算:
1.26÷(-15 )×80.-6.72例1 计算:(-100)×(-20)-(-3). 本题中,先计算乘法,同号为正,再将减法运算转化成加法.分析 原式=100×20+3
=2000+3
=2003.解例2 计算: .有理数的除法法则
两个有理数相除,同号得正,异号得负,并把绝对值相除.
0除以任何非0的数都得0.
除以一个数等于乘以这个数的倒数,即a÷b= a · (b≠0).分析 原式=-11×(-13)×(-13)
=-11×13×13
=-1859-1859解解例3 如图,是一个简单的数值运算程序,当输入x的值为1时,则输出的数值为 . 输入x值为1,即算式为1×(-1)+3=2,所以输出为2..2结 束
同课章节目录
