湘教版七年级数学上册课件:2.2列代数式(共15张PPT)
文档属性
| 名称 | 湘教版七年级数学上册课件:2.2列代数式(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-22 07:36:23 | ||
图片预览




文档简介
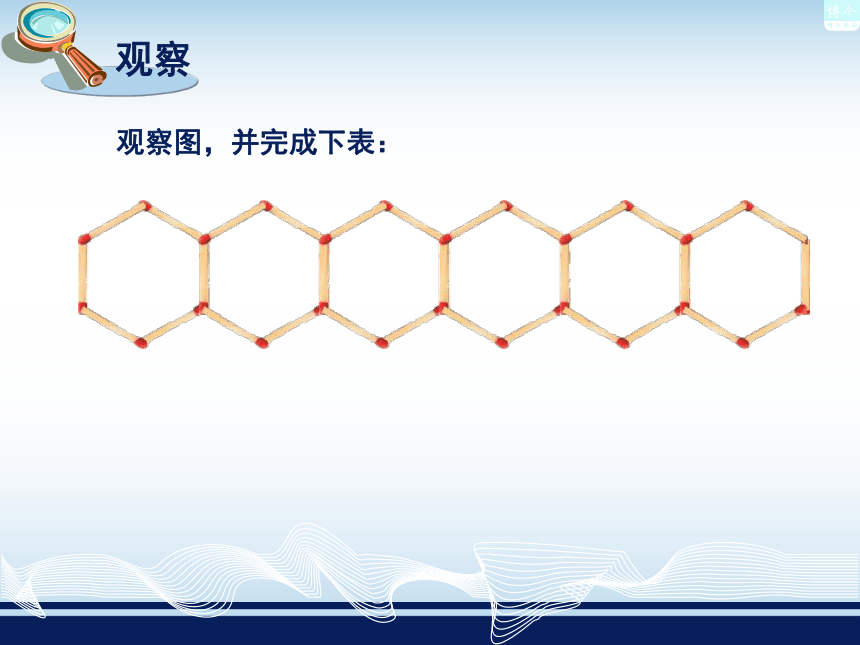
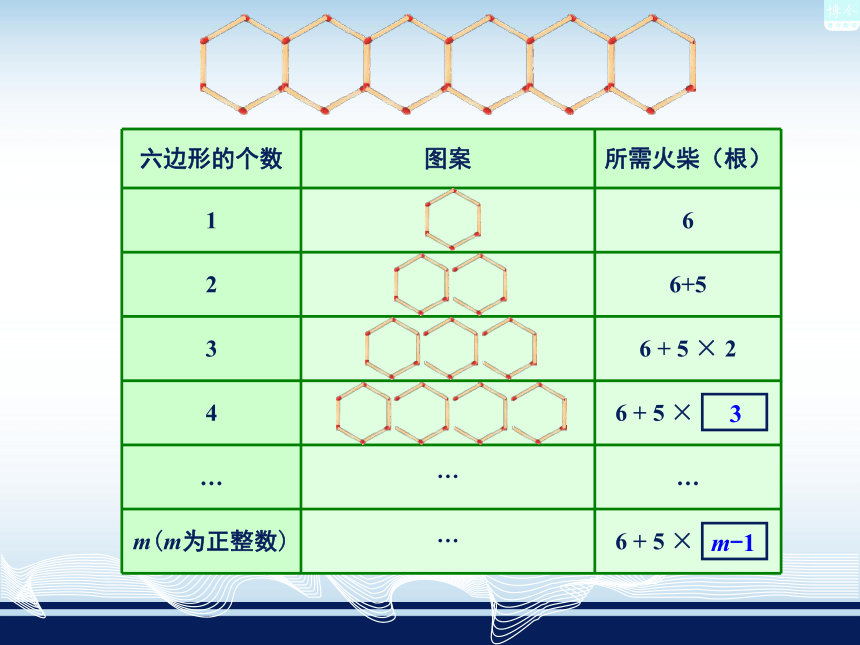
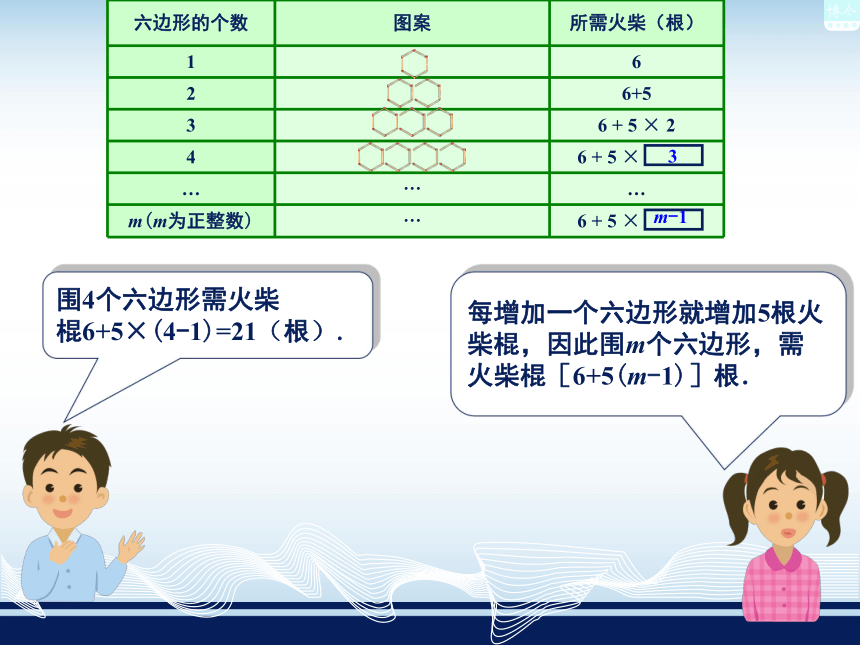
课件15张PPT。列代数式2.2观察图,并完成下表:3m-1围4个六边形需火柴
棍6+5×(4-1)=21(根).每增加一个六边形就增加5根火柴棍,因此围m个六边形,需火柴棍[6+5(m-1)]根.3m-1 单独一个字母或者一个数也是代数式. 前面我们列出了一些式子,如926.6a,ab,2ab, 0.6 a +c, ,6 +5(m-1), 像这样,把数与表示数的字母用运算符号连接而成的式子叫做代数式.例如-5,23, -m,n都是代数式.例1 用代数式表示:
(1)a的7倍与2b的差;
(2)x, y 两数的平方和减去两数积的2倍;
(3)a的倒数与b的和. 举
例解 (1) 7a -2b;
(2) x2+ y2-2xy ;
(3) . 例2
(1)已知铅笔每支x元,练习本每本y元.小明买铅笔5支,练习本6本,需多少元?举
例解(1)需(5x+ 6y)元;(2)小兰骑自行车的速度是(v+10)km/h,
从家到学校需 (2)小兰的家距学校5 km,她步行的速度是v km/h. 而骑自行车比步行快10 km/h. 她骑自行车的速度是多少?她骑自行车从家到学校需多长时间?举出实例,说说代数式25a可以表示什么.如果苹果的价格是每千克a元,买25kg苹果则需要25a元.如果用am/s表示小强跑步的速度,则他跑25s所跑的路程为25am.1. 用代数式填空:
(1)某阶梯教室第一排有8个座位,第二排有10个座
位,以后每排都比它前一排多2个座位,那么第n
排有 个座位;
[8+2(n-1)](2)一批货物共x t,第一天售出 ,第二天售出剩下的
一半,还剩下货物 t . [x - x - ( x - x)] (1)a 与b的和的平方; 2. 列代数式:(2)一件进价为x元的商品,卖出后利润率为
25%,那么这件商品的利润是多少元?
(利润=进价×利润率)(a+b)20.25x 元(3)某储户存入一年期定期储蓄10000元,一年期定期储
蓄的年利率为a%,则一年到期后,该储户可得本息
和(本金与利息的和)多少元?(利息=本金×年利
率×年数)10000+10000×a%3. 请你举出实例,说说代数式 可以表示什么.答:一斤苹果a元,买半斤苹果需要 元.解例1 代数式4a可表示的实际意义是 . 如每支钢笔4元,买a支钢笔所需钱数为4a元;
正方形的边长为a,它的周长为4a等.正方形的边长为a,它的周长为4a 本题是要说出实际意义,即找4a的一个问题背景.答案不惟一,只要符合实际意义及代数式的意义即可.解例2 D “x的 与y的和”用代数式表示为( ).
A. (x + y) B.x + + y C. x + y D. x + y 列代数式时,根据语序确定运算顺序. 依题意,得 x +y.故,应选择D结 束
棍6+5×(4-1)=21(根).每增加一个六边形就增加5根火柴棍,因此围m个六边形,需火柴棍[6+5(m-1)]根.3m-1 单独一个字母或者一个数也是代数式. 前面我们列出了一些式子,如926.6a,ab,2ab, 0.6 a +c, ,6 +5(m-1), 像这样,把数与表示数的字母用运算符号连接而成的式子叫做代数式.例如-5,23, -m,n都是代数式.例1 用代数式表示:
(1)a的7倍与2b的差;
(2)x, y 两数的平方和减去两数积的2倍;
(3)a的倒数与b的和. 举
例解 (1) 7a -2b;
(2) x2+ y2-2xy ;
(3) . 例2
(1)已知铅笔每支x元,练习本每本y元.小明买铅笔5支,练习本6本,需多少元?举
例解(1)需(5x+ 6y)元;(2)小兰骑自行车的速度是(v+10)km/h,
从家到学校需 (2)小兰的家距学校5 km,她步行的速度是v km/h. 而骑自行车比步行快10 km/h. 她骑自行车的速度是多少?她骑自行车从家到学校需多长时间?举出实例,说说代数式25a可以表示什么.如果苹果的价格是每千克a元,买25kg苹果则需要25a元.如果用am/s表示小强跑步的速度,则他跑25s所跑的路程为25am.1. 用代数式填空:
(1)某阶梯教室第一排有8个座位,第二排有10个座
位,以后每排都比它前一排多2个座位,那么第n
排有 个座位;
[8+2(n-1)](2)一批货物共x t,第一天售出 ,第二天售出剩下的
一半,还剩下货物 t . [x - x - ( x - x)] (1)a 与b的和的平方; 2. 列代数式:(2)一件进价为x元的商品,卖出后利润率为
25%,那么这件商品的利润是多少元?
(利润=进价×利润率)(a+b)20.25x 元(3)某储户存入一年期定期储蓄10000元,一年期定期储
蓄的年利率为a%,则一年到期后,该储户可得本息
和(本金与利息的和)多少元?(利息=本金×年利
率×年数)10000+10000×a%3. 请你举出实例,说说代数式 可以表示什么.答:一斤苹果a元,买半斤苹果需要 元.解例1 代数式4a可表示的实际意义是 . 如每支钢笔4元,买a支钢笔所需钱数为4a元;
正方形的边长为a,它的周长为4a等.正方形的边长为a,它的周长为4a 本题是要说出实际意义,即找4a的一个问题背景.答案不惟一,只要符合实际意义及代数式的意义即可.解例2 D “x的 与y的和”用代数式表示为( ).
A. (x + y) B.x + + y C. x + y D. x + y 列代数式时,根据语序确定运算顺序. 依题意,得 x +y.故,应选择D结 束
同课章节目录
