湘教版七年级数学上册课件:3.1建立一元一次方程模型(共20张PPT)
文档属性
| 名称 | 湘教版七年级数学上册课件:3.1建立一元一次方程模型(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-22 07:44:32 | ||
图片预览








文档简介
课件20张PPT。一元一次方程第3章建立一元一次方程模型3.1请你表示出下面两个问题中的等量关系.(1)如图,甲、乙两站之间的高速铁路长1068km,
“和谐号”高速列车从甲站开出2.5h后,离乙站
还有318 km.该高速列车的平均速度是多少?问题(1)的等量关系是:
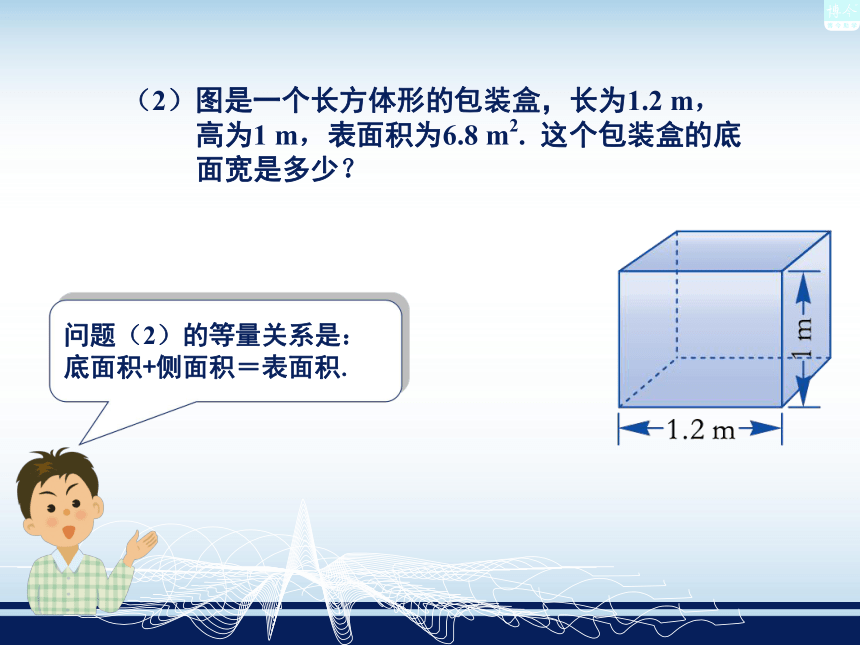
已行驶的路程+剩余的路程= 全长. 如果设高速列车的平均速度为x km/ h,那么我们可以用含x 的式子表示上述等量关系,即 2.5x + 318 = 1068. ①(2)图是一个长方体形的包装盒,长为1.2 m,
高为1 m,表面积为6.8 m2. 这个包装盒的底
面宽是多少?问题(2)的等量关系是:底面积+侧面积=表面积. 若设包装盒的底面宽是 y m,则等量关系可表示为
1.2×y×2+y×1×2+1.2×1×2 = 6.8,即 2.4y + 2y + 2.4= 6.8. ② 在等式2.5x+318 =1068中,2.5,318,1068 叫做已知数,字母x表示的数,在解决这个问题之前还不知道,把它叫做未知数.我们把含有未知数的等式叫做方程. 像上面这样,把所要求的量用字母x(或y,…)表示,根据问题中的等量关系列出方程,这一过程叫做建立方程. 如 2.5x+318=1068,2.4y+2y+2.4=6.8,x-2y=6,
中,x, y, t 都是未知数,这些等式都是方程. 方程①、②中,每个方程含有几个未知数?每个未知数的次数是多少? 像方程2.5x+318=1068,2.4y+2y+2.4=6.8这样,只含有一个未知数,并且未知数的次数是1,我们把这样的方程叫做一元一次方程. 在方程x+5=8中,当x=3时,方程两边的值相等,我们就说x=3是方程x+5=8的解. 能使方程左、右两边相等的未知数的值叫做方程的解.例 检验下列x的值是否是方程2.5x+318=1068的解.
(1) x = 300 (2) x = 330.举
例解(1) 把 x = 300 代入原方程得,
左边= 2.5×300+318=1068,
左边=右边,
所以x=300是方程2.5x+318=1068的解.(2) 把 x =330 代入原方程得,
左边= 2.5×330+318=1143,
左边≠右边,
所以x=330不是方程2.5x+318=1068的解.1. 下面哪些方程是一元一次方程?(1)3x+ 4 = 5x -1;
(2)2x2 - x - 1 = 0 ;
(3)x-2y=4;
(4)3(2x-7)=4(x- 5).是一元一次方程不是一元一次方程不是一元一次方程是一元一次方程2. 检验下列x的值是否是方程2x-6=7x+4的解.(1)x=2 (2)x=-2解 把 x = 2 代入方程左右两边
左边 = 2×2-6=-2
右边 = 7×2+4=18
左边 ≠ 右边
所以 x=2 不是方程2x-6=7x+4的解. 把 x = -2 代入方程左右两边
左边 = 2×(-2)-6=-10
右边=7×(-2)+4=-10
左边=右边
所以 x=-2 是方程2x-6=7x+4的解.(1)x=2(2)x=-23. 建立下列各问题中的方程模型:(1)2011年6月底,我国网民达4.85亿,比2008年6月
底的1.9倍还多430万人,则2008年6月底网民数是
多少? 解 设2008年6月底网民数为x 亿人.
根据题意,得
1.9x +0.043 = 4.85(2)排球场的长比宽多9m,周长是54m,排球场
宽为多少? 解 设排球场的宽为x m,
根据题意,得
2(x+x+9)= 54解例1 关于x的方程2(x-1)-a=0的解是3,则a的值是 ( ).
A.4 B.-4 C. 5 D.-5 本题中,应用方程的解的概念解题.把 x=3代入方程,得
2(3-1)-a=0
解之,得 a=4
故,应选择AA解例2 利用方程的定义对四个选项进行判断可知应选择D,因为D中不含未知数,它不符合方程的定义.
故,应选择D. 下列说法错误的是 ( ).
A. 3x-2x=5x是方程 B. x=0是方程
C. 2x-3y=1是方程 D. π=3.14是方程D结 束
“和谐号”高速列车从甲站开出2.5h后,离乙站
还有318 km.该高速列车的平均速度是多少?问题(1)的等量关系是:
已行驶的路程+剩余的路程= 全长. 如果设高速列车的平均速度为x km/ h,那么我们可以用含x 的式子表示上述等量关系,即 2.5x + 318 = 1068. ①(2)图是一个长方体形的包装盒,长为1.2 m,
高为1 m,表面积为6.8 m2. 这个包装盒的底
面宽是多少?问题(2)的等量关系是:底面积+侧面积=表面积. 若设包装盒的底面宽是 y m,则等量关系可表示为
1.2×y×2+y×1×2+1.2×1×2 = 6.8,即 2.4y + 2y + 2.4= 6.8. ② 在等式2.5x+318 =1068中,2.5,318,1068 叫做已知数,字母x表示的数,在解决这个问题之前还不知道,把它叫做未知数.我们把含有未知数的等式叫做方程. 像上面这样,把所要求的量用字母x(或y,…)表示,根据问题中的等量关系列出方程,这一过程叫做建立方程. 如 2.5x+318=1068,2.4y+2y+2.4=6.8,x-2y=6,
中,x, y, t 都是未知数,这些等式都是方程. 方程①、②中,每个方程含有几个未知数?每个未知数的次数是多少? 像方程2.5x+318=1068,2.4y+2y+2.4=6.8这样,只含有一个未知数,并且未知数的次数是1,我们把这样的方程叫做一元一次方程. 在方程x+5=8中,当x=3时,方程两边的值相等,我们就说x=3是方程x+5=8的解. 能使方程左、右两边相等的未知数的值叫做方程的解.例 检验下列x的值是否是方程2.5x+318=1068的解.
(1) x = 300 (2) x = 330.举
例解(1) 把 x = 300 代入原方程得,
左边= 2.5×300+318=1068,
左边=右边,
所以x=300是方程2.5x+318=1068的解.(2) 把 x =330 代入原方程得,
左边= 2.5×330+318=1143,
左边≠右边,
所以x=330不是方程2.5x+318=1068的解.1. 下面哪些方程是一元一次方程?(1)3x+ 4 = 5x -1;
(2)2x2 - x - 1 = 0 ;
(3)x-2y=4;
(4)3(2x-7)=4(x- 5).是一元一次方程不是一元一次方程不是一元一次方程是一元一次方程2. 检验下列x的值是否是方程2x-6=7x+4的解.(1)x=2 (2)x=-2解 把 x = 2 代入方程左右两边
左边 = 2×2-6=-2
右边 = 7×2+4=18
左边 ≠ 右边
所以 x=2 不是方程2x-6=7x+4的解. 把 x = -2 代入方程左右两边
左边 = 2×(-2)-6=-10
右边=7×(-2)+4=-10
左边=右边
所以 x=-2 是方程2x-6=7x+4的解.(1)x=2(2)x=-23. 建立下列各问题中的方程模型:(1)2011年6月底,我国网民达4.85亿,比2008年6月
底的1.9倍还多430万人,则2008年6月底网民数是
多少? 解 设2008年6月底网民数为x 亿人.
根据题意,得
1.9x +0.043 = 4.85(2)排球场的长比宽多9m,周长是54m,排球场
宽为多少? 解 设排球场的宽为x m,
根据题意,得
2(x+x+9)= 54解例1 关于x的方程2(x-1)-a=0的解是3,则a的值是 ( ).
A.4 B.-4 C. 5 D.-5 本题中,应用方程的解的概念解题.把 x=3代入方程,得
2(3-1)-a=0
解之,得 a=4
故,应选择AA解例2 利用方程的定义对四个选项进行判断可知应选择D,因为D中不含未知数,它不符合方程的定义.
故,应选择D. 下列说法错误的是 ( ).
A. 3x-2x=5x是方程 B. x=0是方程
C. 2x-3y=1是方程 D. π=3.14是方程D结 束
同课章节目录
