物理人教版(2019)必修第二册5.4抛体运动的规律(共18张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册5.4抛体运动的规律(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-01-14 11:45:30 | ||
图片预览





文档简介
(共18张PPT)
5.4 抛体运动的规律
v
A
O
x
y
t
θ
vx
vy
v0
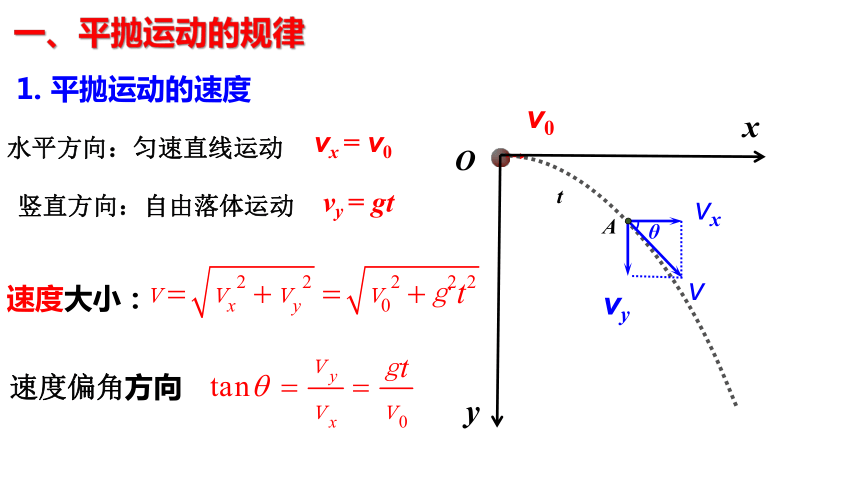
vx = v0
vy = gt
速度偏角方向
水平方向:匀速直线运动
竖直方向:自由落体运动
1. 平抛运动的速度
速度大小:
一、平抛运动的规律
【例1】 (多选)关于平抛物体的运动,以下说法正确的是( )
A.做平抛运动的物体,速度和加速度都随时间的增加而增大
B.做平抛运动的物体仅受到重力的作用,所以加速度保持不变
C.平抛物体的运动是匀变速运动
D.平抛物体的运动是匀速运动
BC
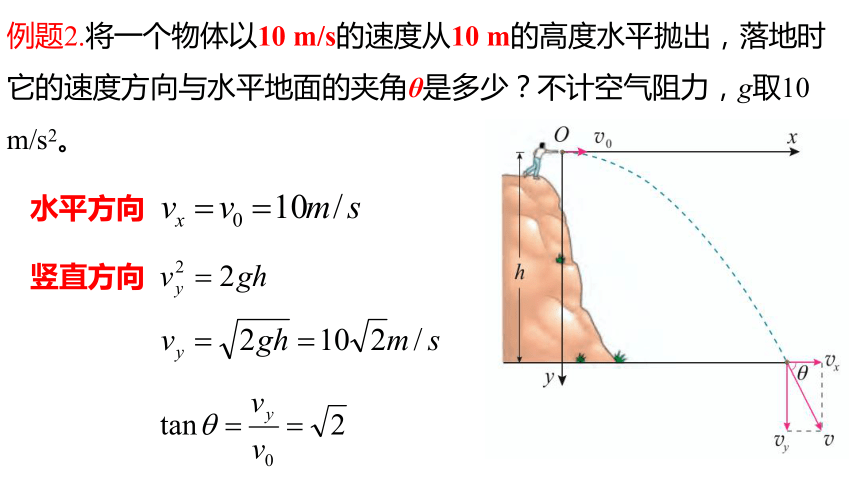
例题2.将一个物体以10 m/s的速度从10 m的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少?不计空气阻力,g取10 m/s2。
竖直方向
水平方向
A
O
x
y
t
v0
x = v0t
(4)位移方向:
α
x
y
(3)合位移:
(1)水平分位移:
(2)竖直分位移:
(5)轨迹方程:
平抛运动的轨迹是抛物线
2. 平抛运动的位移和轨迹
位移偏角
例3.(多选)如图,高为h=1.25 m的平台上覆盖一层薄冰,现有一质量为60 kg的滑雪爱好者以一定的初速度v向平台边缘滑去,着地时速度的方向与水平地面的夹角为45°(重力加速度g取10 m/s2,不计空气阻力)。由此可知下列各项正确的是( )
A.滑雪者在平台上的速度大小是5 m/s
B.滑雪者着地点到平台边缘的水平距离是2.5 m
C.滑雪者在空中运动的时间为1 s
D.着地时滑雪者的速度大小是5 m/s
例题4. 如图,某同学利用无人机玩“投弹”游戏。无 人机以 v0 = 2 m/s 的速度水平向右匀速飞行,在某时刻释放了一个小球。此时无人机到水平地面的距离 h = 20 m,空气阻力忽略不计,g 取 10 m/s2 。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
(2)小球落地点与释放点之间的水平距离
推论1:做平抛运动的物体,设其位移偏向角为α,速度偏向角为θ,则在任意时刻、任意位置有tanθ=2tanα。
v0
vx
v
vy
x
y
5.如图,小球从斜面的顶端A处以大小为v0的初速度水平抛出,恰好落到斜面底部的B点,且此时的速度大小vB=v0,空气阻力不计,该斜面的倾角为( )
A.60°
B.45°
C.37°
D.30°
B
推论2:做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图。
3.平抛运动速度变化情况
B
O
x
y
v0
vA
A
vB
vC
C
v0
vA
vB
vC
任意相等时间 Δt 内的速度变化量相同。
方向恒为竖直向下
Δv = gΔt
位移:x=voxt= v0tcosθ
位移:
速度:vy=v0y-gt=v0sin θ-gt
速度:vx=v0x=v0cosθ
匀速直线运动
竖直上抛运动
X 轴 :
Y 轴:
v0
x
v0x
y
0
v
vx
vy
s
y
x
二、一般的抛体运动(化曲为直)
v0y
建系
在水平地面上斜上抛一个小球,忽略空气阻力,当小球以多大的角度被抛出时,落到同一水平地面上的距离最远
提示:以45°角斜向上抛出时落到同一水平地面上的距离最远。
例6.(多选)如图,从地面上同一位置抛出两小球A、B,分别落在地面上的M、N点,两球运动的最大高度相同。空气阻力不计,则( )
A.B的加速度比A的大
B.B的飞行时间比A的长
C.B在最高点的速度比A在最高点的大
D.B在落地时的速度比A在落地时的大
CD
三、与斜面、弧面相关的平抛运动
例7.(多选)如图,倾角为30°的斜面体固定在水平地面上,斜面底端正上方某高度处有一小球以水平速度v0抛出,恰好垂直打在斜面上。已知重力加速度为g,不计空气阻力。下列说法正确的是( )
A.小球从抛出到落在斜面上的运动时间为
B.小球从抛出到落在斜面上的运动时间为
C.小球抛出时距斜面底端的高度为
D.小球抛出时距斜面底端的高度为
AD
例8.如图,B为竖直圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α。一小球在圆轨道左侧的A点以速度v0平抛,恰好沿B点的切线方向进入圆轨道。已知重力加速度为g,则AB之间的水平距离为( )
A
例9.如图,窗子上、下沿间的高度H=1.6 m,墙的厚度d=0.4 m,某人在离墙壁距离l=1.4 m、距窗子上沿高h=0.2 m处的P点,将可视为质点的小物体以速度v垂直于墙壁水平抛出,小物体直接穿过窗口并落在水平地面上,g取10 m/s2,则v的取值范围是( )
A.v>7 m/s B.v>2.3 m/s
C.3 m/sC
5.4 抛体运动的规律
v
A
O
x
y
t
θ
vx
vy
v0
vx = v0
vy = gt
速度偏角方向
水平方向:匀速直线运动
竖直方向:自由落体运动
1. 平抛运动的速度
速度大小:
一、平抛运动的规律
【例1】 (多选)关于平抛物体的运动,以下说法正确的是( )
A.做平抛运动的物体,速度和加速度都随时间的增加而增大
B.做平抛运动的物体仅受到重力的作用,所以加速度保持不变
C.平抛物体的运动是匀变速运动
D.平抛物体的运动是匀速运动
BC
例题2.将一个物体以10 m/s的速度从10 m的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少?不计空气阻力,g取10 m/s2。
竖直方向
水平方向
A
O
x
y
t
v0
x = v0t
(4)位移方向:
α
x
y
(3)合位移:
(1)水平分位移:
(2)竖直分位移:
(5)轨迹方程:
平抛运动的轨迹是抛物线
2. 平抛运动的位移和轨迹
位移偏角
例3.(多选)如图,高为h=1.25 m的平台上覆盖一层薄冰,现有一质量为60 kg的滑雪爱好者以一定的初速度v向平台边缘滑去,着地时速度的方向与水平地面的夹角为45°(重力加速度g取10 m/s2,不计空气阻力)。由此可知下列各项正确的是( )
A.滑雪者在平台上的速度大小是5 m/s
B.滑雪者着地点到平台边缘的水平距离是2.5 m
C.滑雪者在空中运动的时间为1 s
D.着地时滑雪者的速度大小是5 m/s
例题4. 如图,某同学利用无人机玩“投弹”游戏。无 人机以 v0 = 2 m/s 的速度水平向右匀速飞行,在某时刻释放了一个小球。此时无人机到水平地面的距离 h = 20 m,空气阻力忽略不计,g 取 10 m/s2 。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
(2)小球落地点与释放点之间的水平距离
推论1:做平抛运动的物体,设其位移偏向角为α,速度偏向角为θ,则在任意时刻、任意位置有tanθ=2tanα。
v0
vx
v
vy
x
y
5.如图,小球从斜面的顶端A处以大小为v0的初速度水平抛出,恰好落到斜面底部的B点,且此时的速度大小vB=v0,空气阻力不计,该斜面的倾角为( )
A.60°
B.45°
C.37°
D.30°
B
推论2:做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图。
3.平抛运动速度变化情况
B
O
x
y
v0
vA
A
vB
vC
C
v0
vA
vB
vC
任意相等时间 Δt 内的速度变化量相同。
方向恒为竖直向下
Δv = gΔt
位移:x=voxt= v0tcosθ
位移:
速度:vy=v0y-gt=v0sin θ-gt
速度:vx=v0x=v0cosθ
匀速直线运动
竖直上抛运动
X 轴 :
Y 轴:
v0
x
v0x
y
0
v
vx
vy
s
y
x
二、一般的抛体运动(化曲为直)
v0y
建系
在水平地面上斜上抛一个小球,忽略空气阻力,当小球以多大的角度被抛出时,落到同一水平地面上的距离最远
提示:以45°角斜向上抛出时落到同一水平地面上的距离最远。
例6.(多选)如图,从地面上同一位置抛出两小球A、B,分别落在地面上的M、N点,两球运动的最大高度相同。空气阻力不计,则( )
A.B的加速度比A的大
B.B的飞行时间比A的长
C.B在最高点的速度比A在最高点的大
D.B在落地时的速度比A在落地时的大
CD
三、与斜面、弧面相关的平抛运动
例7.(多选)如图,倾角为30°的斜面体固定在水平地面上,斜面底端正上方某高度处有一小球以水平速度v0抛出,恰好垂直打在斜面上。已知重力加速度为g,不计空气阻力。下列说法正确的是( )
A.小球从抛出到落在斜面上的运动时间为
B.小球从抛出到落在斜面上的运动时间为
C.小球抛出时距斜面底端的高度为
D.小球抛出时距斜面底端的高度为
AD
例8.如图,B为竖直圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α。一小球在圆轨道左侧的A点以速度v0平抛,恰好沿B点的切线方向进入圆轨道。已知重力加速度为g,则AB之间的水平距离为( )
A
例9.如图,窗子上、下沿间的高度H=1.6 m,墙的厚度d=0.4 m,某人在离墙壁距离l=1.4 m、距窗子上沿高h=0.2 m处的P点,将可视为质点的小物体以速度v垂直于墙壁水平抛出,小物体直接穿过窗口并落在水平地面上,g取10 m/s2,则v的取值范围是( )
A.v>7 m/s B.v>2.3 m/s
C.3 m/s
