2024年鲁教版(五四制)中考数学一轮复习 一次函数专题复习专题6.3 一次函数与等腰三角形综合训练(无答案)
文档属性
| 名称 | 2024年鲁教版(五四制)中考数学一轮复习 一次函数专题复习专题6.3 一次函数与等腰三角形综合训练(无答案) | 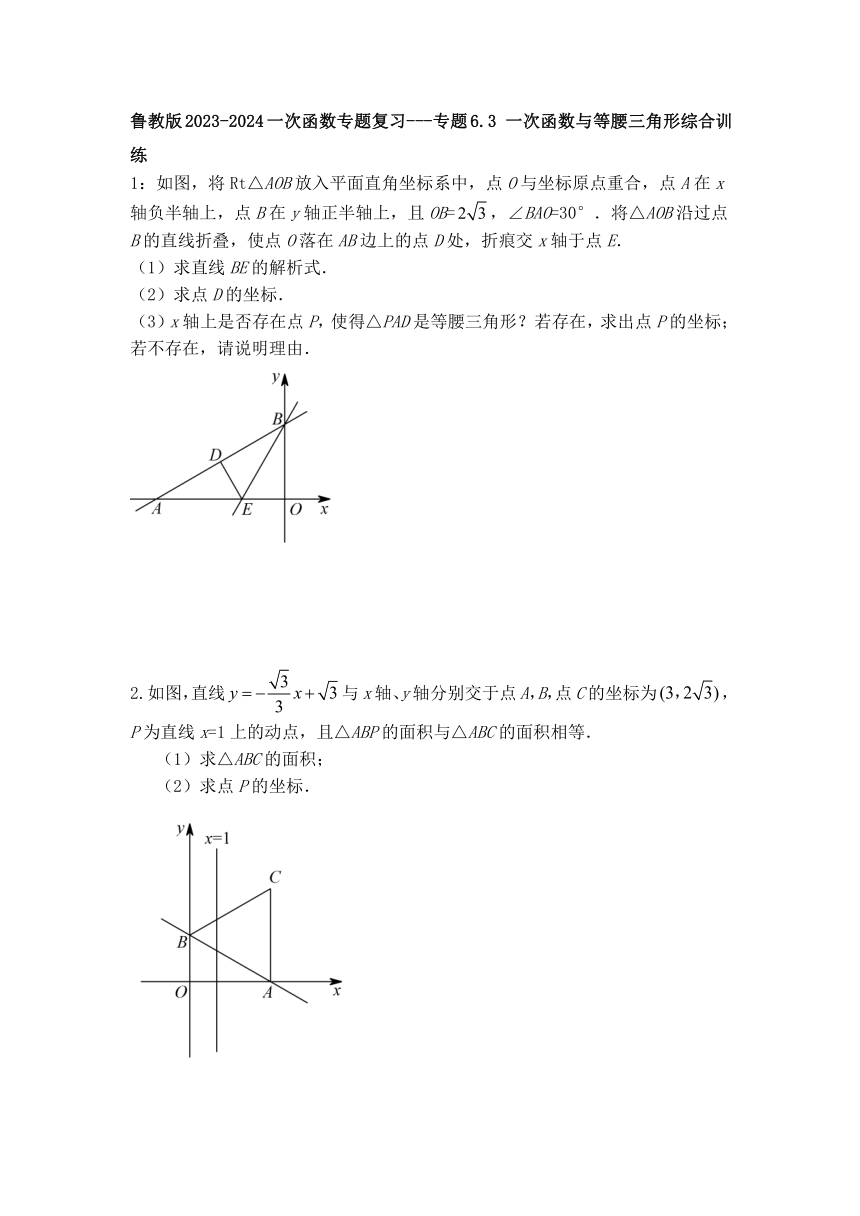 | |
| 格式 | docx | ||
| 文件大小 | 198.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 14:53:39 | ||
图片预览



文档简介
鲁教版2023-2024一次函数专题复习---专题6.3 一次函数与等腰三角形综合训练
1:如图,将Rt△AOB放入平面直角坐标系中,点O与坐标原点重合,点A在x轴负半轴上,点B在y轴正半轴上,且OB=,∠BAO=30°.将△AOB沿过点B的直线折叠,使点O落在AB边上的点D处,折痕交x轴于点E.
(1)求直线BE的解析式.
(2)求点D的坐标.
(3)x轴上是否存在点P,使得△PAD是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
2.如图,直线与x轴、y轴分别交于点A,B,点C的坐标为,P为直线x=1上的动点,且△ABP的面积与△ABC的面积相等.
(1)求△ABC的面积;
(2)求点P的坐标.
3.如图,在平面直角坐标系中,直线AB与x轴、y轴相交于A(6,0)、B(0,2)两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.
(1)求证:△BOC≌△CED;
(2)求经过A、B两点的一次函数表达式及点D的坐标;
(3)在x轴上是否存在点P,使得以C、D、P为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标.(不用写过程)
4.如图直线l:y=kx+b与x轴、y轴分别交于点B、C两点,点B的坐标是(﹣8,0),点C的坐标为(0,6).
(1)求直线l的函数表达式;
(2)若点A的坐标为(﹣6,0),点P是直线l在第二象限内一个动点,当点P运动到什么位置时,△PAC的面积为3,求出此时点P的坐标;
(3)在x轴上是否存在一点M,使得△BCM为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
5.如图,在平面直角坐标系中,正比例函数y=kx与一次函数y=﹣x+b的图象相交于点A(4,3),过点P(0,4)作x轴的平行线,分别交y=kx的图象于点B,交y=﹣x+b的图象于点C,连接OC.
(1)求这两个函数的表达式;
(2)求△OBC的面积;
(3)在坐标轴上存在点M,使△AOM是以OA为腰的等腰三角形,请直接写出点M的坐标.
6.如图1,已知直线与直线AC:y=﹣2x+b交于点A(1,2),两直线与x轴分别交于点B和点C.
(1)求直线AB和AC的函数表达式;
(2)求四边形AFOC的面积;
(3)如图2,点P为线段BC上一动点,将△ABP沿直线AP翻折得到△APD,线段AD交x轴于点E.当△DPE为直角三角形时,请直接写出点P的坐标.
7如图,一次函数y=﹣x+3的图象与x轴、y轴分别相交于点A、B,将△AOB沿直线CD对折,使点A和点B重合,直线CD与x轴交于点C,与AB交于点D.
(1)求A,B两点的坐标;
(2)在x轴上是否存在点P,使△PAB为等腰三角形?如果存在,写出点P的坐标;如果不存在,说明理由.
8如图1,平面直角坐标系中,一次函数图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C,点P是直线AB上的一个动点.
(1)求直线BC的表达式与点C的坐标;
(2)如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
(3)试探究x轴上是否存在点M,使以A,B,M为顶点的三角形是等腰三角形.若存在,直接写出点M的坐标;若不存在,说明理由.
9如图,一次函数y=kx+b的图象经过点A(0,5),并与直线y=x相交于点B,与x轴相交于点C,其中点B的横坐标为2.
(1)求B点的坐标和k,b的值;
(2)如图2,点Q为线段AC上(不与A、C重合)一动点,过点Q分别作OA和OC的垂线,垂足为E、F.点Q在何处时,矩形OFQE的面积为3?
(3)在y轴上是否存在点P使△PAB为等腰三角形?若存在,请直接写出点P坐标;若不存在,请说明理由
10.如图1,已知直线与x轴交于点A,与y轴交于点B,直线l2与y轴交于点,与直线l1交于点D(2,t).
(1)求直线l2的解析式;(2)如图2,若点P在直线l1上,过点P作轴交l2于点Q,交x轴于点G,使,求此时P点的坐标;(3)将直线向左平移10个单位得到直线l3交x轴于点E,点F是点C关于原点的对称点,过点F作直线轴.在直线l4上是否存在动点M,使得为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
11.如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,连接DA并延长,交y轴于点E.
(1)求证:△OBC≌△ABD;
(2)若以A,E,C为顶点的三角形是等腰三角形,求点C的坐标.
12.如图,在平面直角坐标系中,过点A(﹣,0)的两条直线分别交y轴于B(0,m)、C(0,n)两点,且m、n(m>n)满足方程组的解.
(1)求证:AC⊥AB;
(2)若点D在直线AC上,且DB=DC,求点D的坐标;
(3)在(2)的条件下,在直线BD上寻找点P,使以A、B、P三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
1:如图,将Rt△AOB放入平面直角坐标系中,点O与坐标原点重合,点A在x轴负半轴上,点B在y轴正半轴上,且OB=,∠BAO=30°.将△AOB沿过点B的直线折叠,使点O落在AB边上的点D处,折痕交x轴于点E.
(1)求直线BE的解析式.
(2)求点D的坐标.
(3)x轴上是否存在点P,使得△PAD是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
2.如图,直线与x轴、y轴分别交于点A,B,点C的坐标为,P为直线x=1上的动点,且△ABP的面积与△ABC的面积相等.
(1)求△ABC的面积;
(2)求点P的坐标.
3.如图,在平面直角坐标系中,直线AB与x轴、y轴相交于A(6,0)、B(0,2)两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.
(1)求证:△BOC≌△CED;
(2)求经过A、B两点的一次函数表达式及点D的坐标;
(3)在x轴上是否存在点P,使得以C、D、P为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标.(不用写过程)
4.如图直线l:y=kx+b与x轴、y轴分别交于点B、C两点,点B的坐标是(﹣8,0),点C的坐标为(0,6).
(1)求直线l的函数表达式;
(2)若点A的坐标为(﹣6,0),点P是直线l在第二象限内一个动点,当点P运动到什么位置时,△PAC的面积为3,求出此时点P的坐标;
(3)在x轴上是否存在一点M,使得△BCM为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
5.如图,在平面直角坐标系中,正比例函数y=kx与一次函数y=﹣x+b的图象相交于点A(4,3),过点P(0,4)作x轴的平行线,分别交y=kx的图象于点B,交y=﹣x+b的图象于点C,连接OC.
(1)求这两个函数的表达式;
(2)求△OBC的面积;
(3)在坐标轴上存在点M,使△AOM是以OA为腰的等腰三角形,请直接写出点M的坐标.
6.如图1,已知直线与直线AC:y=﹣2x+b交于点A(1,2),两直线与x轴分别交于点B和点C.
(1)求直线AB和AC的函数表达式;
(2)求四边形AFOC的面积;
(3)如图2,点P为线段BC上一动点,将△ABP沿直线AP翻折得到△APD,线段AD交x轴于点E.当△DPE为直角三角形时,请直接写出点P的坐标.
7如图,一次函数y=﹣x+3的图象与x轴、y轴分别相交于点A、B,将△AOB沿直线CD对折,使点A和点B重合,直线CD与x轴交于点C,与AB交于点D.
(1)求A,B两点的坐标;
(2)在x轴上是否存在点P,使△PAB为等腰三角形?如果存在,写出点P的坐标;如果不存在,说明理由.
8如图1,平面直角坐标系中,一次函数图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C,点P是直线AB上的一个动点.
(1)求直线BC的表达式与点C的坐标;
(2)如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
(3)试探究x轴上是否存在点M,使以A,B,M为顶点的三角形是等腰三角形.若存在,直接写出点M的坐标;若不存在,说明理由.
9如图,一次函数y=kx+b的图象经过点A(0,5),并与直线y=x相交于点B,与x轴相交于点C,其中点B的横坐标为2.
(1)求B点的坐标和k,b的值;
(2)如图2,点Q为线段AC上(不与A、C重合)一动点,过点Q分别作OA和OC的垂线,垂足为E、F.点Q在何处时,矩形OFQE的面积为3?
(3)在y轴上是否存在点P使△PAB为等腰三角形?若存在,请直接写出点P坐标;若不存在,请说明理由
10.如图1,已知直线与x轴交于点A,与y轴交于点B,直线l2与y轴交于点,与直线l1交于点D(2,t).
(1)求直线l2的解析式;(2)如图2,若点P在直线l1上,过点P作轴交l2于点Q,交x轴于点G,使,求此时P点的坐标;(3)将直线向左平移10个单位得到直线l3交x轴于点E,点F是点C关于原点的对称点,过点F作直线轴.在直线l4上是否存在动点M,使得为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
11.如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,连接DA并延长,交y轴于点E.
(1)求证:△OBC≌△ABD;
(2)若以A,E,C为顶点的三角形是等腰三角形,求点C的坐标.
12.如图,在平面直角坐标系中,过点A(﹣,0)的两条直线分别交y轴于B(0,m)、C(0,n)两点,且m、n(m>n)满足方程组的解.
(1)求证:AC⊥AB;
(2)若点D在直线AC上,且DB=DC,求点D的坐标;
(3)在(2)的条件下,在直线BD上寻找点P,使以A、B、P三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
同课章节目录
