2024年中考数学第一轮综合复习——锐角三角函数(含答案)
文档属性
| 名称 | 2024年中考数学第一轮综合复习——锐角三角函数(含答案) |  | |
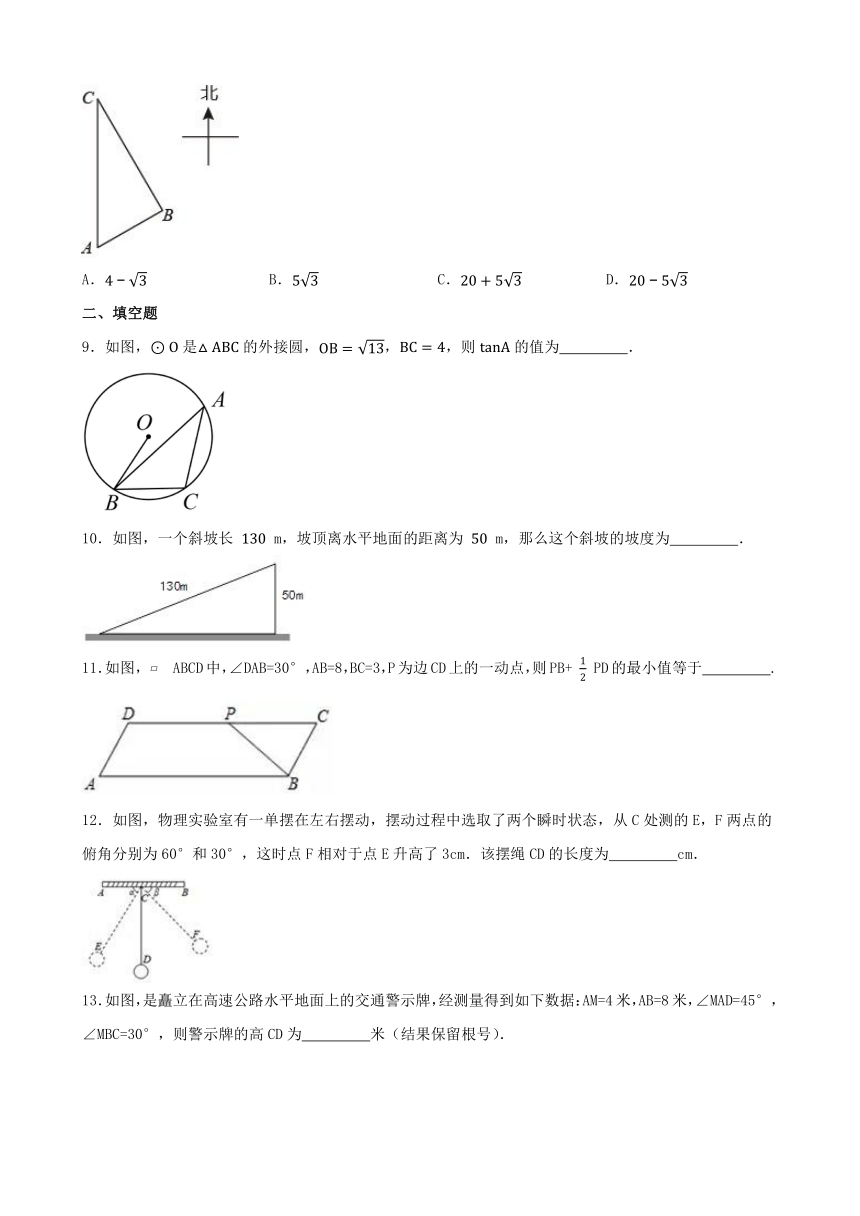
| 格式 | docx | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 14:36:18 | ||
图片预览


文档简介
2024年中考数学第一轮综合复习——锐角三角函数
一、单选题
1.在Rt△ABC中,若各边的长度同时都扩大2倍,则锐角A的正弦值与余弦值的情况( )
A.都扩大2倍
B.都缩小2倍
C.都不变
D.正弦值扩大2倍,余弦值缩小2倍
2.如图,在Rt△ABC中,∠C=90°,sinA= ,BC=4,则AC的长为( )
A.6 B.5 C. D.
3.如图,点A在x轴上,点B,C在y轴上,则下列结论正确的是( )
A. B.
C. D.
4.如图,AB是⊙O的直径,点C是AB延长线上的一点,CD与⊙O相切于点D,连接AD,BD.若∠C=30°,则( )
A.BC+BD=CD B.AB+BD=CD C.BC+CD=AB D.AD+AC=AB
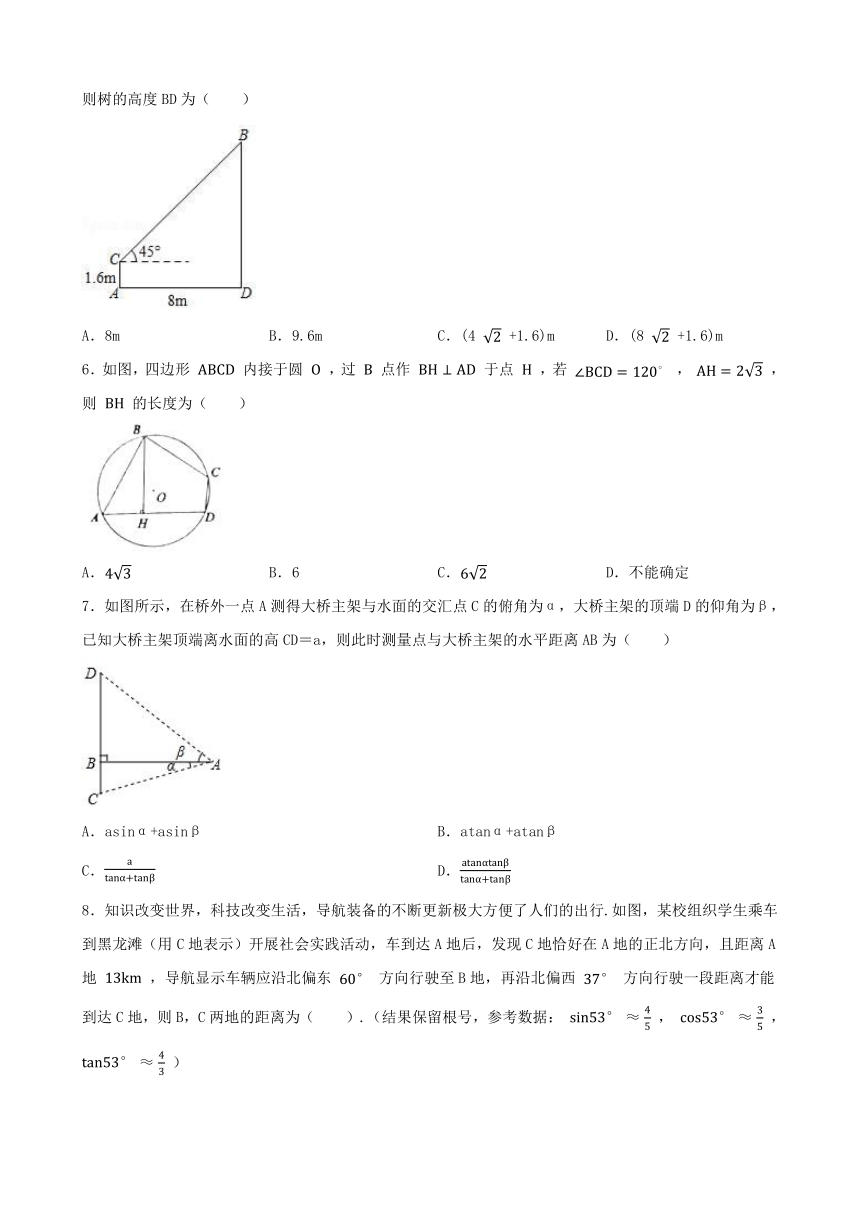
5.如图,护林员在离树8m的A处测得树顶B的仰角为45°,已知护林员的眼睛离地面的距离AC为1.6m,则树的高度BD为( )
A.8m B.9.6m C.(4 +1.6)m D.(8 +1.6)m
6.如图,四边形 内接于圆 ,过 点作 于点 ,若 , ,则 的长度为( )
A. B.6 C. D.不能确定
7.如图所示,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知大桥主架顶端离水面的高CD=a,则此时测量点与大桥主架的水平距离AB为( )
A.asinα+asinβ B.atanα+atanβ
C. D.
8.知识改变世界,科技改变生活,导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C地表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地 ,导航显示车辆应沿北偏东 方向行驶至B地,再沿北偏西 方向行驶一段距离才能到达C地,则B,C两地的距离为( ).(结果保留根号,参考数据: , , )
A. B. C. D.
二、填空题
9.如图,是的外接圆,,,则的值为 .
10.如图,一个斜坡长 m,坡顶离水平地面的距离为 m,那么这个斜坡的坡度为 .
11.如图, ABCD中,∠DAB=30°,AB=8,BC=3,P为边CD上的一动点,则PB+ PD的最小值等于 .
12.如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测的E,F两点的俯角分别为60°和30°,这时点F相对于点E升高了3cm.该摆绳CD的长度为 cm.
13.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米(结果保留根号).
三、解答题
14.如图,某海岸边有B,C两码头,C码头位于B码头的正东方向,距B码头40海里.甲、乙两船同时从A岛出发,甲船向位于A岛正北方向的B码头航行,乙船向位于A岛北偏东 方向的C码头航行,当甲船到达距B码头30海里的E处时,乙船位于甲船北偏东 方向的D处,求此时乙船与C码头之间的距离.(结果保留根号)
15.如图,小明去年到普陀山游玩,上山时乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200m,缆车行驶的路线与水平夹角∠α=18°,当缆车继续由点B到达点D时,它又走过了200m,缆车由点B到点D的行驶路线与水平面夹角∠β=46°,求缆车从点A到点D垂直上升的距离(结果保留整数)(参考数据:sin18°≈0.31,cos18°≈0.95,sin46°≈0.72,cos46°≈0.70)
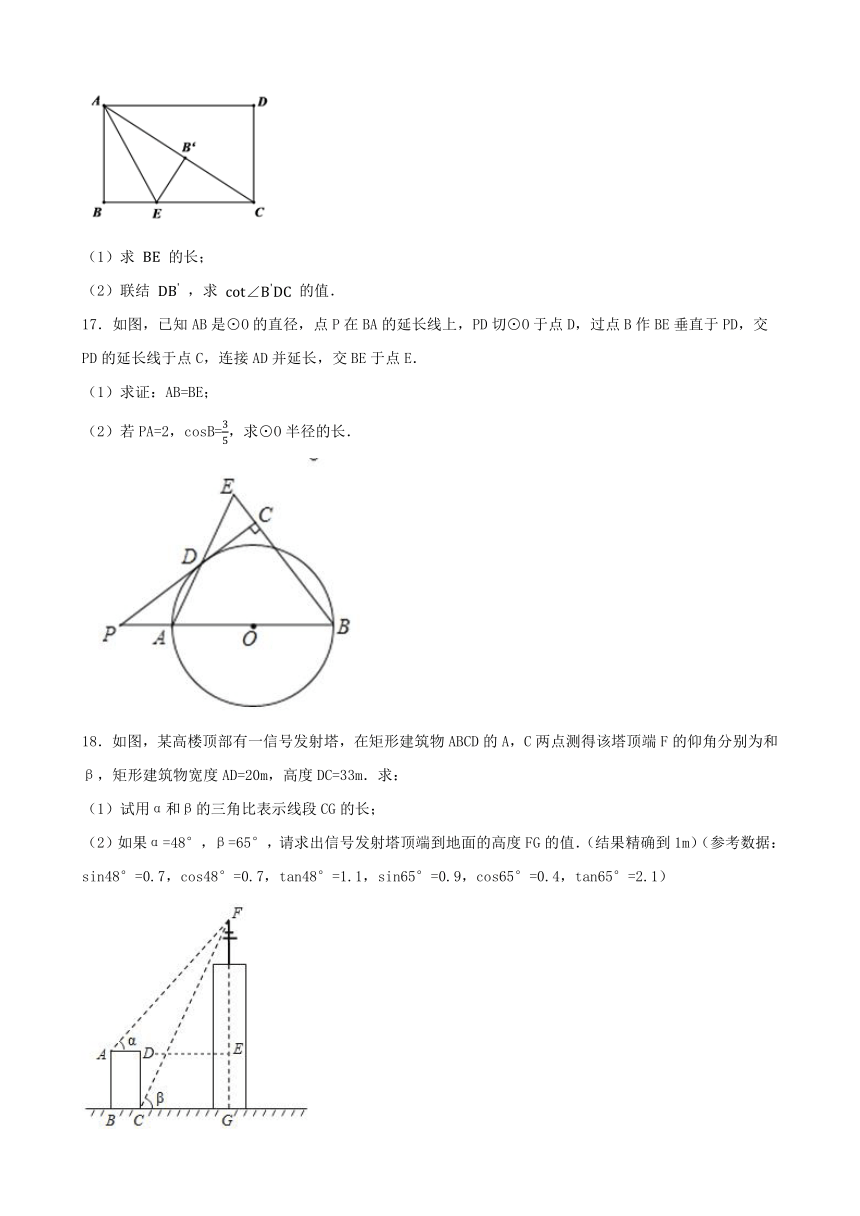
16.如图,矩形 中, 为边 上一点,将 沿 翻折,使点 恰好落在对角线 上,记作 ,
(1)求 的长;
(2)联结 ,求 的值.
17.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB=,求⊙O半径的长.
18.如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为和β,矩形建筑物宽度AD=20m,高度DC=33m.求:
(1)试用α和β的三角比表示线段CG的长;
(2)如果α=48°,β=65°,请求出信号发射塔顶端到地面的高度FG的值.(结果精确到1m)(参考数据:sin48°=0.7,cos48°=0.7,tan48°=1.1,sin65°=0.9,cos65°=0.4,tan65°=2.1)
答案
1.C
2.C
3.D
4.B
5.B
6.B
7.C
8.C
9.
10.1:2.4
11.4
12.
13. 一4
14.解:方法1:
解:如图1,延长 交 延长线于点F,
由题意得 ,
, ,
,
.
在 中, ,
,
,
,
(海里),
答:此时乙船与C码头之间的距离为 海里.
方法2:
解:如图2,
过点D作 于点M, 于点N,则四边形 为矩形.
.
在 中, ,
, ,
.
.
,
,
,
.
在 中, .
,
, .
.
在 中, ,
,
(海里).
答:此时乙船与C码头之间的距离为 海里.
方法3:解:如图2,过点D作 于点M, 于点N,则四边形 为矩形.
.
设 ,则 ,
在 中, ,
,
, ,
.
在 中,
,
.
(海里).
答:此时乙船与C码头之间的距离为 (海里).
方法4:
如图3,过点E作 于点G,
在 中, ,
,
,
.
在 中, ,
,
,
,
,
,
.
于点G,
,
(海里).
答:此时乙船与C码头之间的距离为 海里.
15.解:在Rt△ABC中,AB-200米,∠a= 18° ∴BC= AB sin =200×0.31 = 62米 在Rt△BDF中,BD=200米,∠β=46° ∴DF = BD sinβ = 200×0.72= 144米 ∴垂直上升的距离为:BC+DF=144+62=206米
16.(1)解: 四边形ABCD是矩形, ,
,
在 中, ,即 ,
解得 ,
,
由翻折的性质得: ,
,
设 ,则 ,
在 中, ,即 ,
解得 ,
即BE的长为 ;
(2)解:如图,过点 作 于点F,
,
,
,
,
在 中, ,即 ,
解得 ,
,
则在 中, .
17.(1)证明:连接OD,∵PD切⊙O于点D,∴OD⊥PD,∵BE⊥PC,∴OD∥BE,∴ADO=∠E,∵OA=OD,∴∠OAD=∠ADO,∴∠OAD=∠E,∴AB=BE;(2)解:由(1)知,OD∥BE,∴∠POD=∠B,∴cos∠POD=cosB=,在Rt△POD中,cos∠POD==,∵OD=OA,PO=PA+OA=2+OA,∴=,∴OA=3,∴⊙O半径=3.
18.解:(1)设CG=xm,
由图可知:EF=(x+20) tanα,FG=x tanβ,
则(x+20)tanα+33=xtanβ,
解得x= ;
(2)x== =55,
则FG=x tanβ=55×2.1=115.5≈116.
答:该信号发射塔顶端到地面的高度FG约是116m
一、单选题
1.在Rt△ABC中,若各边的长度同时都扩大2倍,则锐角A的正弦值与余弦值的情况( )
A.都扩大2倍
B.都缩小2倍
C.都不变
D.正弦值扩大2倍,余弦值缩小2倍
2.如图,在Rt△ABC中,∠C=90°,sinA= ,BC=4,则AC的长为( )
A.6 B.5 C. D.
3.如图,点A在x轴上,点B,C在y轴上,则下列结论正确的是( )
A. B.
C. D.
4.如图,AB是⊙O的直径,点C是AB延长线上的一点,CD与⊙O相切于点D,连接AD,BD.若∠C=30°,则( )
A.BC+BD=CD B.AB+BD=CD C.BC+CD=AB D.AD+AC=AB
5.如图,护林员在离树8m的A处测得树顶B的仰角为45°,已知护林员的眼睛离地面的距离AC为1.6m,则树的高度BD为( )
A.8m B.9.6m C.(4 +1.6)m D.(8 +1.6)m
6.如图,四边形 内接于圆 ,过 点作 于点 ,若 , ,则 的长度为( )
A. B.6 C. D.不能确定
7.如图所示,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知大桥主架顶端离水面的高CD=a,则此时测量点与大桥主架的水平距离AB为( )
A.asinα+asinβ B.atanα+atanβ
C. D.
8.知识改变世界,科技改变生活,导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C地表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地 ,导航显示车辆应沿北偏东 方向行驶至B地,再沿北偏西 方向行驶一段距离才能到达C地,则B,C两地的距离为( ).(结果保留根号,参考数据: , , )
A. B. C. D.
二、填空题
9.如图,是的外接圆,,,则的值为 .
10.如图,一个斜坡长 m,坡顶离水平地面的距离为 m,那么这个斜坡的坡度为 .
11.如图, ABCD中,∠DAB=30°,AB=8,BC=3,P为边CD上的一动点,则PB+ PD的最小值等于 .
12.如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测的E,F两点的俯角分别为60°和30°,这时点F相对于点E升高了3cm.该摆绳CD的长度为 cm.
13.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米(结果保留根号).
三、解答题
14.如图,某海岸边有B,C两码头,C码头位于B码头的正东方向,距B码头40海里.甲、乙两船同时从A岛出发,甲船向位于A岛正北方向的B码头航行,乙船向位于A岛北偏东 方向的C码头航行,当甲船到达距B码头30海里的E处时,乙船位于甲船北偏东 方向的D处,求此时乙船与C码头之间的距离.(结果保留根号)
15.如图,小明去年到普陀山游玩,上山时乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200m,缆车行驶的路线与水平夹角∠α=18°,当缆车继续由点B到达点D时,它又走过了200m,缆车由点B到点D的行驶路线与水平面夹角∠β=46°,求缆车从点A到点D垂直上升的距离(结果保留整数)(参考数据:sin18°≈0.31,cos18°≈0.95,sin46°≈0.72,cos46°≈0.70)
16.如图,矩形 中, 为边 上一点,将 沿 翻折,使点 恰好落在对角线 上,记作 ,
(1)求 的长;
(2)联结 ,求 的值.
17.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB=,求⊙O半径的长.
18.如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为和β,矩形建筑物宽度AD=20m,高度DC=33m.求:
(1)试用α和β的三角比表示线段CG的长;
(2)如果α=48°,β=65°,请求出信号发射塔顶端到地面的高度FG的值.(结果精确到1m)(参考数据:sin48°=0.7,cos48°=0.7,tan48°=1.1,sin65°=0.9,cos65°=0.4,tan65°=2.1)
答案
1.C
2.C
3.D
4.B
5.B
6.B
7.C
8.C
9.
10.1:2.4
11.4
12.
13. 一4
14.解:方法1:
解:如图1,延长 交 延长线于点F,
由题意得 ,
, ,
,
.
在 中, ,
,
,
,
(海里),
答:此时乙船与C码头之间的距离为 海里.
方法2:
解:如图2,
过点D作 于点M, 于点N,则四边形 为矩形.
.
在 中, ,
, ,
.
.
,
,
,
.
在 中, .
,
, .
.
在 中, ,
,
(海里).
答:此时乙船与C码头之间的距离为 海里.
方法3:解:如图2,过点D作 于点M, 于点N,则四边形 为矩形.
.
设 ,则 ,
在 中, ,
,
, ,
.
在 中,
,
.
(海里).
答:此时乙船与C码头之间的距离为 (海里).
方法4:
如图3,过点E作 于点G,
在 中, ,
,
,
.
在 中, ,
,
,
,
,
,
.
于点G,
,
(海里).
答:此时乙船与C码头之间的距离为 海里.
15.解:在Rt△ABC中,AB-200米,∠a= 18° ∴BC= AB sin =200×0.31 = 62米 在Rt△BDF中,BD=200米,∠β=46° ∴DF = BD sinβ = 200×0.72= 144米 ∴垂直上升的距离为:BC+DF=144+62=206米
16.(1)解: 四边形ABCD是矩形, ,
,
在 中, ,即 ,
解得 ,
,
由翻折的性质得: ,
,
设 ,则 ,
在 中, ,即 ,
解得 ,
即BE的长为 ;
(2)解:如图,过点 作 于点F,
,
,
,
,
在 中, ,即 ,
解得 ,
,
则在 中, .
17.(1)证明:连接OD,∵PD切⊙O于点D,∴OD⊥PD,∵BE⊥PC,∴OD∥BE,∴ADO=∠E,∵OA=OD,∴∠OAD=∠ADO,∴∠OAD=∠E,∴AB=BE;(2)解:由(1)知,OD∥BE,∴∠POD=∠B,∴cos∠POD=cosB=,在Rt△POD中,cos∠POD==,∵OD=OA,PO=PA+OA=2+OA,∴=,∴OA=3,∴⊙O半径=3.
18.解:(1)设CG=xm,
由图可知:EF=(x+20) tanα,FG=x tanβ,
则(x+20)tanα+33=xtanβ,
解得x= ;
(2)x== =55,
则FG=x tanβ=55×2.1=115.5≈116.
答:该信号发射塔顶端到地面的高度FG约是116m
同课章节目录
