2024年中考数学复习专题综合训练:二次函数(含答案)
文档属性
| 名称 | 2024年中考数学复习专题综合训练:二次函数(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 290.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 14:34:30 | ||
图片预览




文档简介
2024年中考数学复习专题综合训练:二次函数
一、选择题
1.下列函数中,是二次函数的是( )
A.y=x2+ B.y=x(x-1) C.y=-2x-1 D.y=x(x2+1).
2.抛物线的顶点坐标是( )
A. B. C. D.
3.把抛物线向左平移2个单位,再向上平移3个单位,得到的抛物线是( )
A. B.
C. D.
4.函数y=ax2与y=﹣ax+b的图象可能是( )
A.B.C.D.
5.如图,是二次函数y=ax2+bx+c图象的一部分,则a的取值范围是( )
A.a>1 B.a>2 C.0<a<1 D.0<a<2
6.已知抛物线过点,,,则,,的大小关系是( )
A. B. C. D.
7.抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a= ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
A.5 B.4 C.3 D.2
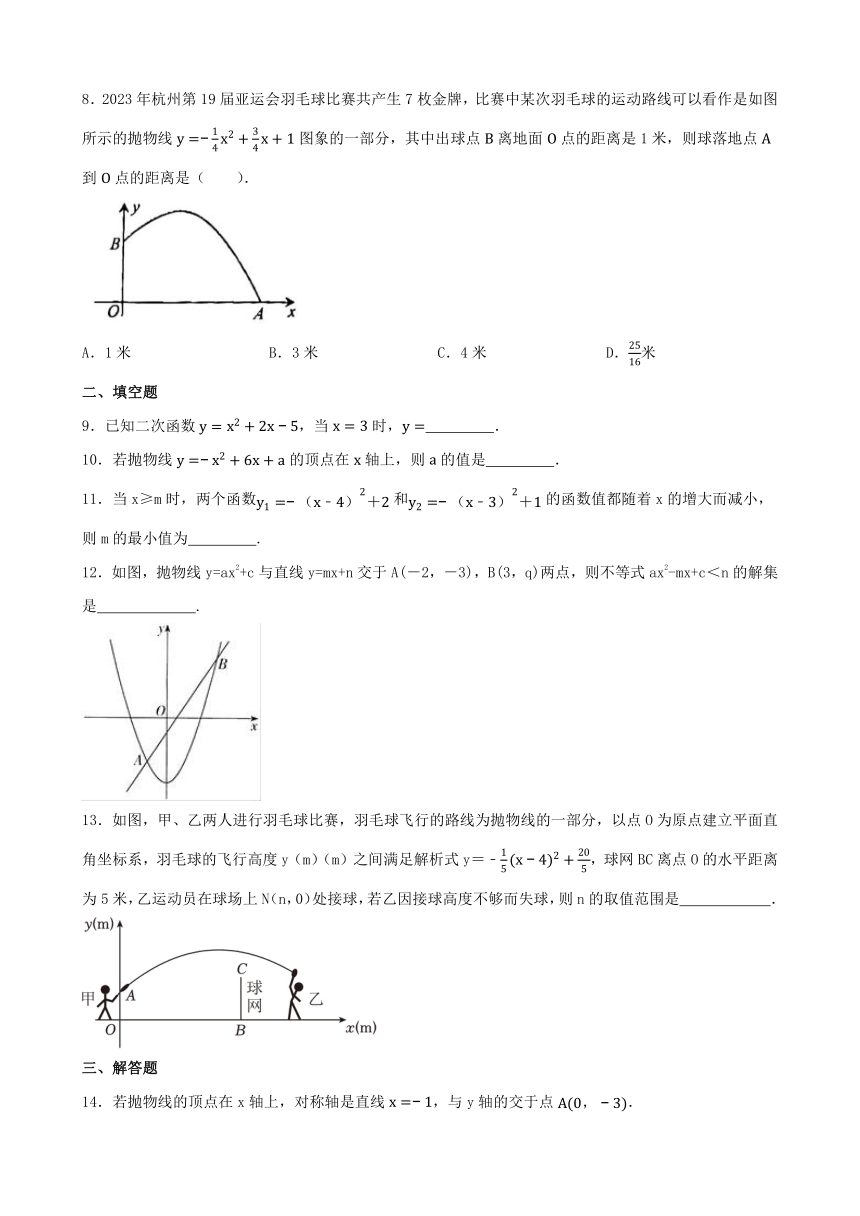
8.2023年杭州第19届亚运会羽毛球比赛共产生7枚金牌,比赛中某次羽毛球的运动路线可以看作是如图所示的抛物线图象的一部分,其中出球点离地面点的距离是1米,则球落地点到点的距离是( ).
A.1米 B.3米 C.4米 D.米
二、填空题
9.已知二次函数,当时, .
10.若抛物线的顶点在轴上,则的值是 .
11.当x≥m时,两个函数和的函数值都随着x的增大而减小,则m的最小值为 .
12.如图,抛物线y=ax2+c与直线y=mx+n交于A(-2,-3),B(3,q)两点,则不等式ax2-mx+c<n的解集是 .
13.如图,甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,以点O为原点建立平面直角坐标系,羽毛球的飞行高度y(m)(m)之间满足解析式y=﹣,球网BC离点O的水平距离为5米,乙运动员在球场上N(n,0)处接球,若乙因接球高度不够而失球,则n的取值范围是 .
三、解答题
14.若抛物线的顶点在x轴上,对称轴是直线,与y轴的交于点.
(1)求抛物线的解析式;
(2)写出它的顶点坐标和开口方向;
(3)当x取何值时,抛物线中y随x增大而增大.
15.已知二次函数y=x2+bx+c的图象经过点(2,﹣3),(﹣1,12).
(1)求b,c的值;
(2)若点A(m,k),B(n,k)在二次函数y=x2+bx+c图象上,其中m+n,当﹣2<m<1时,求n的取值范围.
16.端午节吃粽子是中华民族的传统习俗,市场上豆沙粽的进价比肉粽的进价每盒便宜10元,某商家用8000元购进的肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒,设肉粽每盒售价x元,y表示该商家每天销售肉粽的利润(单位:元).
(1)肉粽和豆沙粽每盒的进价分别为多少元
(2)若每盒利润率不超过50%,问肉粽价格为多少元时,商家每天获利1350元?
(3)若x满足,求商家每天的最大利润.
17.如图,已知抛物线与x轴交于,两点,与y轴交于点C.
(1)求该抛物线的表达式;
(2)若点P是抛物线上的一点,且,求点P的坐标;
(3)设直线的表达式为,若关于x的一元一次方程有两个正实数根,直接写出n的取值范围.
18.如图,抛物线与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为,,点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作轴于点D.若,的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
参考答案
1.B
2.A
3.C
4.B
5.C
6.D
7.C
8.C
9.10
10.-9
11.4
12.-2<x<3
13.5<n<7
14.(1)解:∵抛物线的顶点在x轴上,对称轴是直线,
∴抛物线的顶点坐标为,
设抛物线解析式为,
把代入得,
解得,
所以抛物线解析式为
(2)解:由(1)得:它的顶点坐标为,开口向下
(3)解:因为抛物线开口向下,对称轴是直线,
所以当时,y随x增大而增大.
15.解:(1)∵函数y=x2+bx+c的图象经过点(2,﹣3),(﹣1,12),
∴,
∴;
(2)∵b=﹣6,c=5,
∴y=x2﹣6x+5,
∴函数的对称轴为直线x=3,
∵点A(m,k),B(n,k)在二次函数图象上,
∴A点与B点关于对称轴对称,
∴m+n=6,
∴m=6﹣n,
∵﹣2<m<1,
∴﹣2<6﹣n<1,
∴5<n<8.
16.(1)解:设肉粽每盒进价a元,则豆沙粽每盒进价元.
则,
解得,
经检验是方程的解,
.
答:肉粽每盒40元,豆沙粽每盒30元;
(2)解:∵肉粽进价每盒40元,每盒利润率不超过50%,
∴,
由题意得,,
整理得,,
解得(舍去),.
答:肉粽价格为55元时,商家每天获利1350元;
(3)解:设商家的利润为y元,
则,
配方得,,
∵时,y随x的增大而增大,,
∴当时,y取最大值,.
答:最大利润为1600元.
17.(1)解:∵抛物线与x轴交于,两点,
∴,
解得:,
∴抛物线的表达式为
(2)解:如图所示:
①当点P在x轴上方时,过点P作轴于点E,
∵,
∴,
∵,
∴,
∵,
设,,
∴点P的坐标为,
∵点P是抛物线上一点,
∴,
解得:,(不合题意,舍去),
∴点P坐标为;
②当点在x轴下方时,过点作轴于点F,
∵,
∴,
∵,
∴,
设,则,
∴点的坐标为,
∵点是抛物线上一点,
∴,
解得:,(不符合题意,舍去),
∴点的坐标为,
综上所述:点P坐标为或
(3)解:
18.(1)解:把、代入,
得,
解得,
∴二次函数的解析式为.
(2)解:有最大值.理由如下:
如图1,设直线的解析式为,
,
∴该抛物线的顶点坐标为,
把、代入,得,
解得,
∴,
,
∴;
由,
得;
∵当点与点重合时,不存在以、、为顶点的三角形,
∴,
∴不存在最小值;
,
∴当时,,
∴的最大值为.
(3)解:存在,理由如下:
若,如图2,则轴,
∴,且在直线上,
∴,
解得,
∴;
若,如图3,则,
∴,
整理,得,
解得,(不符合题意,舍去);
∴,;
若,则,
∴,
整理,得,
解得,
此时不存在以,,为顶点的三角形,
∴舍去.
综上所述,点的坐标为或.
一、选择题
1.下列函数中,是二次函数的是( )
A.y=x2+ B.y=x(x-1) C.y=-2x-1 D.y=x(x2+1).
2.抛物线的顶点坐标是( )
A. B. C. D.
3.把抛物线向左平移2个单位,再向上平移3个单位,得到的抛物线是( )
A. B.
C. D.
4.函数y=ax2与y=﹣ax+b的图象可能是( )
A.B.C.D.
5.如图,是二次函数y=ax2+bx+c图象的一部分,则a的取值范围是( )
A.a>1 B.a>2 C.0<a<1 D.0<a<2
6.已知抛物线过点,,,则,,的大小关系是( )
A. B. C. D.
7.抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a= ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
A.5 B.4 C.3 D.2
8.2023年杭州第19届亚运会羽毛球比赛共产生7枚金牌,比赛中某次羽毛球的运动路线可以看作是如图所示的抛物线图象的一部分,其中出球点离地面点的距离是1米,则球落地点到点的距离是( ).
A.1米 B.3米 C.4米 D.米
二、填空题
9.已知二次函数,当时, .
10.若抛物线的顶点在轴上,则的值是 .
11.当x≥m时,两个函数和的函数值都随着x的增大而减小,则m的最小值为 .
12.如图,抛物线y=ax2+c与直线y=mx+n交于A(-2,-3),B(3,q)两点,则不等式ax2-mx+c<n的解集是 .
13.如图,甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,以点O为原点建立平面直角坐标系,羽毛球的飞行高度y(m)(m)之间满足解析式y=﹣,球网BC离点O的水平距离为5米,乙运动员在球场上N(n,0)处接球,若乙因接球高度不够而失球,则n的取值范围是 .
三、解答题
14.若抛物线的顶点在x轴上,对称轴是直线,与y轴的交于点.
(1)求抛物线的解析式;
(2)写出它的顶点坐标和开口方向;
(3)当x取何值时,抛物线中y随x增大而增大.
15.已知二次函数y=x2+bx+c的图象经过点(2,﹣3),(﹣1,12).
(1)求b,c的值;
(2)若点A(m,k),B(n,k)在二次函数y=x2+bx+c图象上,其中m+n,当﹣2<m<1时,求n的取值范围.
16.端午节吃粽子是中华民族的传统习俗,市场上豆沙粽的进价比肉粽的进价每盒便宜10元,某商家用8000元购进的肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒,设肉粽每盒售价x元,y表示该商家每天销售肉粽的利润(单位:元).
(1)肉粽和豆沙粽每盒的进价分别为多少元
(2)若每盒利润率不超过50%,问肉粽价格为多少元时,商家每天获利1350元?
(3)若x满足,求商家每天的最大利润.
17.如图,已知抛物线与x轴交于,两点,与y轴交于点C.
(1)求该抛物线的表达式;
(2)若点P是抛物线上的一点,且,求点P的坐标;
(3)设直线的表达式为,若关于x的一元一次方程有两个正实数根,直接写出n的取值范围.
18.如图,抛物线与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为,,点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作轴于点D.若,的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
参考答案
1.B
2.A
3.C
4.B
5.C
6.D
7.C
8.C
9.10
10.-9
11.4
12.-2<x<3
13.5<n<7
14.(1)解:∵抛物线的顶点在x轴上,对称轴是直线,
∴抛物线的顶点坐标为,
设抛物线解析式为,
把代入得,
解得,
所以抛物线解析式为
(2)解:由(1)得:它的顶点坐标为,开口向下
(3)解:因为抛物线开口向下,对称轴是直线,
所以当时,y随x增大而增大.
15.解:(1)∵函数y=x2+bx+c的图象经过点(2,﹣3),(﹣1,12),
∴,
∴;
(2)∵b=﹣6,c=5,
∴y=x2﹣6x+5,
∴函数的对称轴为直线x=3,
∵点A(m,k),B(n,k)在二次函数图象上,
∴A点与B点关于对称轴对称,
∴m+n=6,
∴m=6﹣n,
∵﹣2<m<1,
∴﹣2<6﹣n<1,
∴5<n<8.
16.(1)解:设肉粽每盒进价a元,则豆沙粽每盒进价元.
则,
解得,
经检验是方程的解,
.
答:肉粽每盒40元,豆沙粽每盒30元;
(2)解:∵肉粽进价每盒40元,每盒利润率不超过50%,
∴,
由题意得,,
整理得,,
解得(舍去),.
答:肉粽价格为55元时,商家每天获利1350元;
(3)解:设商家的利润为y元,
则,
配方得,,
∵时,y随x的增大而增大,,
∴当时,y取最大值,.
答:最大利润为1600元.
17.(1)解:∵抛物线与x轴交于,两点,
∴,
解得:,
∴抛物线的表达式为
(2)解:如图所示:
①当点P在x轴上方时,过点P作轴于点E,
∵,
∴,
∵,
∴,
∵,
设,,
∴点P的坐标为,
∵点P是抛物线上一点,
∴,
解得:,(不合题意,舍去),
∴点P坐标为;
②当点在x轴下方时,过点作轴于点F,
∵,
∴,
∵,
∴,
设,则,
∴点的坐标为,
∵点是抛物线上一点,
∴,
解得:,(不符合题意,舍去),
∴点的坐标为,
综上所述:点P坐标为或
(3)解:
18.(1)解:把、代入,
得,
解得,
∴二次函数的解析式为.
(2)解:有最大值.理由如下:
如图1,设直线的解析式为,
,
∴该抛物线的顶点坐标为,
把、代入,得,
解得,
∴,
,
∴;
由,
得;
∵当点与点重合时,不存在以、、为顶点的三角形,
∴,
∴不存在最小值;
,
∴当时,,
∴的最大值为.
(3)解:存在,理由如下:
若,如图2,则轴,
∴,且在直线上,
∴,
解得,
∴;
若,如图3,则,
∴,
整理,得,
解得,(不符合题意,舍去);
∴,;
若,则,
∴,
整理,得,
解得,
此时不存在以,,为顶点的三角形,
∴舍去.
综上所述,点的坐标为或.
同课章节目录
