2024年中考数学一轮复习练习题:数据的分析(含答案)
文档属性
| 名称 | 2024年中考数学一轮复习练习题:数据的分析(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 397.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 15:05:25 | ||
图片预览



文档简介
2024年中考数学一轮复习练习题:数据的分析
一、单选题
1.一组数据:3,2,5,3,7,5,x,它们的众数为5,则这组数据的中位数是( )
A.2 B.3 C.5 D.7
2.某校篮球班21名同学的身高如下表:则该校蓝球班21名同学身高的众数和中位数分别是(单位:cm)( )
身高cm 183 186 188 192 209
人数(个) 4 6 5 4 2
A.186,186 B.186,187 C.186,188 D.208,188
3.甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位平均成绩较高且状态稳定的同学参加数学比赛,那么应选( )
甲 乙 丙 丁
平均数 80 85 85 80
方差 42 45 54 59
A.甲 B.乙 C.丙 D.丁
4.某班50名同学参加安全知识竞赛成绩统计如下表,其中两个数据被覆盖,关于成绩的四个统计量:①众数,②中位数,③平均数,④方差,一定与被覆盖数据无关的是( )
成绩(分) 93 94 95 96 97 98
人数 ■ 12 14 10 ■ 6
A.①② B.②③ C.③④ D.①④
5.在5轮“中国汉字听写大赛”选拔赛中,甲乙两位同学的平均分都是90分,甲的成绩方差是16,乙的成绩方差是8,下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
6.在同一时期分别从甲、乙、丙,丁四种小麦中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为: = =13cm, = =15cm;S甲2=S丁2=3.6cm2,S乙2=S丙2=6.3cm2,则麦苗又高又齐的是( )
A.甲 B.乙 C.丙 D.丁
7.下表是抽查的某班10名同学中考体育测试成绩线计表.
成绩(分) 30 25 20 15
人数(人) 2 1
若成绩的平均数为23,中位数是 ,众数是 ,则a-b的值是( )
A.﹣5 B.﹣2.5 C.2.5 D.5
8.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表:
如果鞋店要购进100双这种女鞋,那么购进24厘米、24.5厘米和25厘米三种女鞋数量之和最合适的是( ).
A.20双 B.30双 C.50双 D.80双
二、填空题
9.已知一组数据1,3,5,x,y的平均数是3,则另一组数据-1,1,3,x-2,y-2的平均数是 。
10.有7个数由小到大依次排列,其平均数是38,如果这组数的前4个数的平均数是33,后4个数的平均数是42,则这7个数的中位数是 .
11.甲、乙两人5次射击命中的环数如下:
甲:7,9,8,6,10
乙:7,8,9 ,8, 8
则这两人5次射击命中的环数的平均数 = =8,方差 .(填“>”、“<”或“=”)
12.某公司25名员工上月收入如下表:
月收入/元 45000 18000 10000 5500 5000 34000 3000 1000
人数 1 1 1 3 6 1 11 1
这25名员工收入数据的众数是 .
13.小丽参加单位举行的演讲比赛,评分规则及小丽的得分如下表:
演讲内容 语言表达 仪表仪容
所占比例 30% 60% 10%
小丽得分 90 85 75
则小丽的最终演讲评分为 .
三、解答题
14.九(1)班五位同学参加学校举办的数学素养竞赛.试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分.赛后A,B,C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表
参赛同学 答对题数 答错题数 未答题数
A 19 0 1
B 17 2 1
C 15 2 3
D 17 1 2
E / / 7
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知ABCDE五位同学成绩分别是95分,81分,64分,83分,58分.
①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩的平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况,请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可)
15.为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).
根据上述信息,解答下列各题:
(1)该班级女生人数是 女生收看“两会”新闻次数的中位数是
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低5%,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 平均数(次) 中位数(次) 众数(次) 方差 …
该班级男生 3 3 4 2 …
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
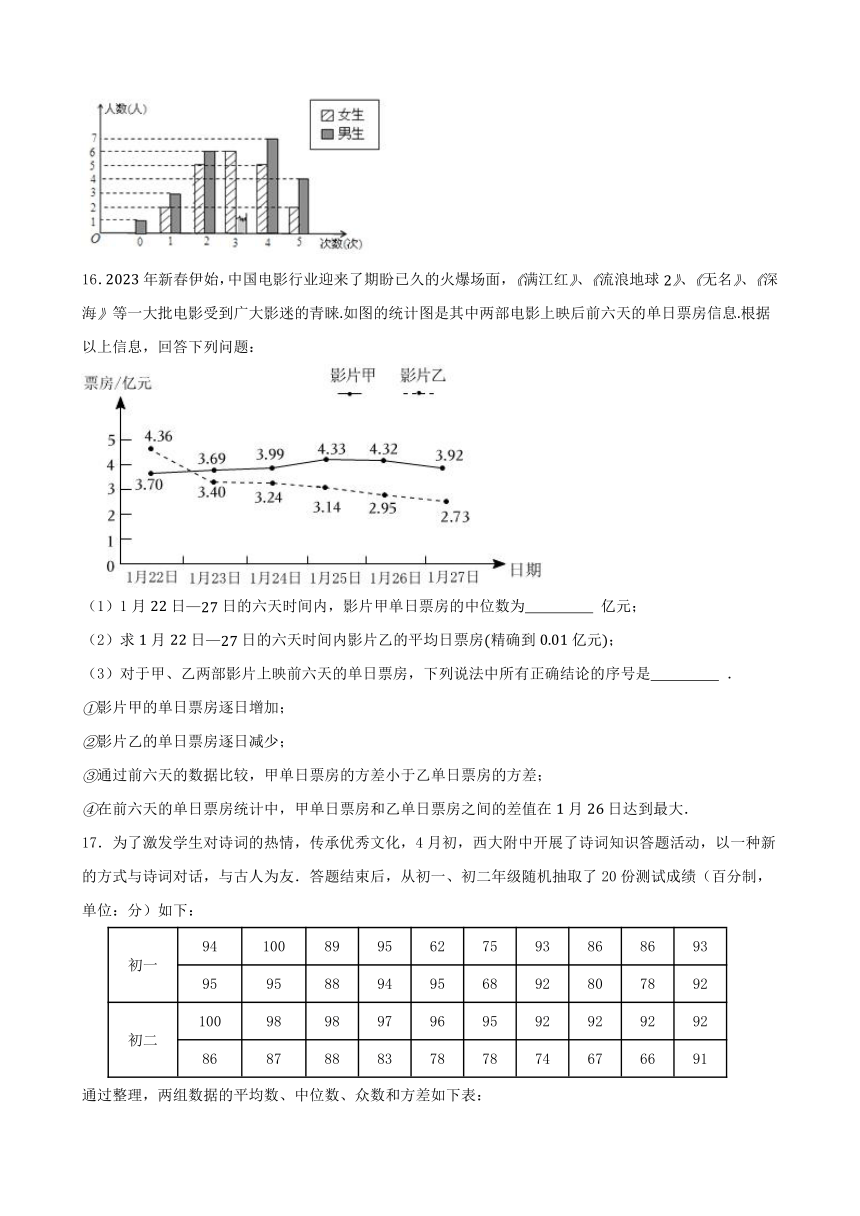
16.年新春伊始,中国电影行业迎来了期盼已久的火爆场面,满江红、流浪地球、无名、深海等一大批电影受到广大影迷的青睐如图的统计图是其中两部电影上映后前六天的单日票房信息根据以上信息,回答下列问题:
(1)1月日日的六天时间内,影片甲单日票房的中位数为 亿元;
(2)求月日日的六天时间内影片乙的平均日票房精确到亿元;
(3)对于甲、乙两部影片上映前六天的单日票房,下列说法中所有正确结论的序号是 .
影片甲的单日票房逐日增加;
影片乙的单日票房逐日减少;
通过前六天的数据比较,甲单日票房的方差小于乙单日票房的方差;
在前六天的单日票房统计中,甲单日票房和乙单日票房之间的差值在月日达到最大.
17.为了激发学生对诗词的热情,传承优秀文化,4月初,西大附中开展了诗词知识答题活动,以一种新的方式与诗词对话,与古人为友.答题结束后,从初一、初二年级随机抽取了20份测试成绩(百分制,单位:分)如下:
初一 94 100 89 95 62 75 93 86 86 93
95 95 88 94 95 68 92 80 78 92
初二 100 98 98 97 96 95 92 92 92 92
86 87 88 83 78 78 74 67 66 91
通过整理,两组数据的平均数、中位数、众数和方差如下表:
平均数 中位数 众数 方差
初一 87.5 92 m 95.35
初二 87.5 n 92 97.85
某同学将初一学生得分按分数段(,,,),绘制成频数分布直方图,初二同学得分绘制成扇形统计图,如下图(均不完整).
初一学生得分频数分布直方图
初二学生得分扇形统计图
请完成下列问题:
(1)初一学生得分的众数 ;初二学生得分的中位数 ;
(2)补全频数分布直方图 ;扇形统计图中,所对应的圆心角为 度;
(3)若初二年级有1200名学生,估计初二年级答题活动中达到优秀()的有多少名?
(4)根据以上数据,你认为初一、初二年级中哪个年级学生诗词知识掌握较好?请说明理由(写出一条理由即可).
18.为了解地铁14号线与7号线的日客运强度,获得了它们2022年1月份工作日(共21天)日客运强度(单位:万人/公里)的数据,并对数据进行整理、描述和分析.下面给出了部分信息:
a.地铁14号线2022年1月份工作日日客运强度的数据的频数分布直方图如下(数据分成6组:0.50≤x<0.70,0.70≤x<0.90,0.90≤x<1.10,1.10≤x<1.30,1.30≤x<1.50,1.50≤x≤1.70);
b.地铁14号线2022年1月份工作日日客运强度的数据在1.30≤x<1.50这一组是:
1.37 1.37 1.37 1.38 1.41 1.47 1.48 1.48 1.49
c.地铁14号线与7号线2022年1月份工作日日客运强度的平均数、中位数如下:
平均数 中位数
地铁14号线 1.37 m
地铁7号线 1.08 1.1
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)日客运强度反映了地铁的拥挤程度,小明每天上班均需乘坐地铁,可以选择乘坐地铁14号线或乘坐地铁7号线.请帮助小明选择一种乘坐地铁的方式,并说明理由;
(3)2022年一共有249个工作日,请估计2022年全年的工作日中,地铁14号线日客运强度不低于1.3万人/公里的天数(直接写出结果).
答案解析部分
1.C
2.C
3.B
4.A
5.B
6.D
7.C
8.B
9.1
10.34
11.>
12.3000
13.85.5
14.解:(1)=[(19+17+15+17)×5+(2+2+1)×(﹣2)]=82.5(分),答:A,B,C,D四位同学成绩的平均分是82.5分;(2)①设E同学答对x题,答错y题,由题意得,解得,答:E同学答对12题,答错1题;②C同学,他实际答对14题,答错3题,未答3题.
15.解:(1)20,3;
(2)由题意:该班女生对“两会”新闻的“关注指数”为
所以,男生对“两会”新闻的“关注指数”为60%
设该班的男生有x人
则,解得:x=25
答:该班级男生有25人.
(3)该班级女生收看“两会”新闻次数的平均数为=3,
女生收看“两会”新闻次数的方差为:=
因为2>,所以男生比女生的波动幅度大.
16.(1)3.955
(2)解:亿元.
影片乙的平均票房约为亿元;
(3)
17.(1)95;
(2)初一学生得分在范围的人数5人,补全频数分布直方图如下: ;初二学生得分在相应的圆心角为,54
(3)解:∵初二年级样本中有11人,
∴(人)
答:估计优秀的学生有人;
(4)解:初一学生诗词知识掌握较好.
理由:初一学生得分的平均分一样,但众数、中位数都比初二的高,方差比初二的小.
18.(1)解:根据条形统计图可得,1+1+2+3+9=16,
14号线的中位数第11个数据在1.30≤x<1.50这一组第4个数据为1.38,
故答案为:1.38;
(2)解:选择7号线,理由如下:
7号线的客运强度的平均数及中位数均小于14号线,说明人流量较小,所以选择7号线;
(3)166天
一、单选题
1.一组数据:3,2,5,3,7,5,x,它们的众数为5,则这组数据的中位数是( )
A.2 B.3 C.5 D.7
2.某校篮球班21名同学的身高如下表:则该校蓝球班21名同学身高的众数和中位数分别是(单位:cm)( )
身高cm 183 186 188 192 209
人数(个) 4 6 5 4 2
A.186,186 B.186,187 C.186,188 D.208,188
3.甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位平均成绩较高且状态稳定的同学参加数学比赛,那么应选( )
甲 乙 丙 丁
平均数 80 85 85 80
方差 42 45 54 59
A.甲 B.乙 C.丙 D.丁
4.某班50名同学参加安全知识竞赛成绩统计如下表,其中两个数据被覆盖,关于成绩的四个统计量:①众数,②中位数,③平均数,④方差,一定与被覆盖数据无关的是( )
成绩(分) 93 94 95 96 97 98
人数 ■ 12 14 10 ■ 6
A.①② B.②③ C.③④ D.①④
5.在5轮“中国汉字听写大赛”选拔赛中,甲乙两位同学的平均分都是90分,甲的成绩方差是16,乙的成绩方差是8,下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
6.在同一时期分别从甲、乙、丙,丁四种小麦中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为: = =13cm, = =15cm;S甲2=S丁2=3.6cm2,S乙2=S丙2=6.3cm2,则麦苗又高又齐的是( )
A.甲 B.乙 C.丙 D.丁
7.下表是抽查的某班10名同学中考体育测试成绩线计表.
成绩(分) 30 25 20 15
人数(人) 2 1
若成绩的平均数为23,中位数是 ,众数是 ,则a-b的值是( )
A.﹣5 B.﹣2.5 C.2.5 D.5
8.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表:
如果鞋店要购进100双这种女鞋,那么购进24厘米、24.5厘米和25厘米三种女鞋数量之和最合适的是( ).
A.20双 B.30双 C.50双 D.80双
二、填空题
9.已知一组数据1,3,5,x,y的平均数是3,则另一组数据-1,1,3,x-2,y-2的平均数是 。
10.有7个数由小到大依次排列,其平均数是38,如果这组数的前4个数的平均数是33,后4个数的平均数是42,则这7个数的中位数是 .
11.甲、乙两人5次射击命中的环数如下:
甲:7,9,8,6,10
乙:7,8,9 ,8, 8
则这两人5次射击命中的环数的平均数 = =8,方差 .(填“>”、“<”或“=”)
12.某公司25名员工上月收入如下表:
月收入/元 45000 18000 10000 5500 5000 34000 3000 1000
人数 1 1 1 3 6 1 11 1
这25名员工收入数据的众数是 .
13.小丽参加单位举行的演讲比赛,评分规则及小丽的得分如下表:
演讲内容 语言表达 仪表仪容
所占比例 30% 60% 10%
小丽得分 90 85 75
则小丽的最终演讲评分为 .
三、解答题
14.九(1)班五位同学参加学校举办的数学素养竞赛.试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分.赛后A,B,C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表
参赛同学 答对题数 答错题数 未答题数
A 19 0 1
B 17 2 1
C 15 2 3
D 17 1 2
E / / 7
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知ABCDE五位同学成绩分别是95分,81分,64分,83分,58分.
①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩的平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况,请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可)
15.为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).
根据上述信息,解答下列各题:
(1)该班级女生人数是 女生收看“两会”新闻次数的中位数是
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低5%,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 平均数(次) 中位数(次) 众数(次) 方差 …
该班级男生 3 3 4 2 …
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
16.年新春伊始,中国电影行业迎来了期盼已久的火爆场面,满江红、流浪地球、无名、深海等一大批电影受到广大影迷的青睐如图的统计图是其中两部电影上映后前六天的单日票房信息根据以上信息,回答下列问题:
(1)1月日日的六天时间内,影片甲单日票房的中位数为 亿元;
(2)求月日日的六天时间内影片乙的平均日票房精确到亿元;
(3)对于甲、乙两部影片上映前六天的单日票房,下列说法中所有正确结论的序号是 .
影片甲的单日票房逐日增加;
影片乙的单日票房逐日减少;
通过前六天的数据比较,甲单日票房的方差小于乙单日票房的方差;
在前六天的单日票房统计中,甲单日票房和乙单日票房之间的差值在月日达到最大.
17.为了激发学生对诗词的热情,传承优秀文化,4月初,西大附中开展了诗词知识答题活动,以一种新的方式与诗词对话,与古人为友.答题结束后,从初一、初二年级随机抽取了20份测试成绩(百分制,单位:分)如下:
初一 94 100 89 95 62 75 93 86 86 93
95 95 88 94 95 68 92 80 78 92
初二 100 98 98 97 96 95 92 92 92 92
86 87 88 83 78 78 74 67 66 91
通过整理,两组数据的平均数、中位数、众数和方差如下表:
平均数 中位数 众数 方差
初一 87.5 92 m 95.35
初二 87.5 n 92 97.85
某同学将初一学生得分按分数段(,,,),绘制成频数分布直方图,初二同学得分绘制成扇形统计图,如下图(均不完整).
初一学生得分频数分布直方图
初二学生得分扇形统计图
请完成下列问题:
(1)初一学生得分的众数 ;初二学生得分的中位数 ;
(2)补全频数分布直方图 ;扇形统计图中,所对应的圆心角为 度;
(3)若初二年级有1200名学生,估计初二年级答题活动中达到优秀()的有多少名?
(4)根据以上数据,你认为初一、初二年级中哪个年级学生诗词知识掌握较好?请说明理由(写出一条理由即可).
18.为了解地铁14号线与7号线的日客运强度,获得了它们2022年1月份工作日(共21天)日客运强度(单位:万人/公里)的数据,并对数据进行整理、描述和分析.下面给出了部分信息:
a.地铁14号线2022年1月份工作日日客运强度的数据的频数分布直方图如下(数据分成6组:0.50≤x<0.70,0.70≤x<0.90,0.90≤x<1.10,1.10≤x<1.30,1.30≤x<1.50,1.50≤x≤1.70);
b.地铁14号线2022年1月份工作日日客运强度的数据在1.30≤x<1.50这一组是:
1.37 1.37 1.37 1.38 1.41 1.47 1.48 1.48 1.49
c.地铁14号线与7号线2022年1月份工作日日客运强度的平均数、中位数如下:
平均数 中位数
地铁14号线 1.37 m
地铁7号线 1.08 1.1
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)日客运强度反映了地铁的拥挤程度,小明每天上班均需乘坐地铁,可以选择乘坐地铁14号线或乘坐地铁7号线.请帮助小明选择一种乘坐地铁的方式,并说明理由;
(3)2022年一共有249个工作日,请估计2022年全年的工作日中,地铁14号线日客运强度不低于1.3万人/公里的天数(直接写出结果).
答案解析部分
1.C
2.C
3.B
4.A
5.B
6.D
7.C
8.B
9.1
10.34
11.>
12.3000
13.85.5
14.解:(1)=[(19+17+15+17)×5+(2+2+1)×(﹣2)]=82.5(分),答:A,B,C,D四位同学成绩的平均分是82.5分;(2)①设E同学答对x题,答错y题,由题意得,解得,答:E同学答对12题,答错1题;②C同学,他实际答对14题,答错3题,未答3题.
15.解:(1)20,3;
(2)由题意:该班女生对“两会”新闻的“关注指数”为
所以,男生对“两会”新闻的“关注指数”为60%
设该班的男生有x人
则,解得:x=25
答:该班级男生有25人.
(3)该班级女生收看“两会”新闻次数的平均数为=3,
女生收看“两会”新闻次数的方差为:=
因为2>,所以男生比女生的波动幅度大.
16.(1)3.955
(2)解:亿元.
影片乙的平均票房约为亿元;
(3)
17.(1)95;
(2)初一学生得分在范围的人数5人,补全频数分布直方图如下: ;初二学生得分在相应的圆心角为,54
(3)解:∵初二年级样本中有11人,
∴(人)
答:估计优秀的学生有人;
(4)解:初一学生诗词知识掌握较好.
理由:初一学生得分的平均分一样,但众数、中位数都比初二的高,方差比初二的小.
18.(1)解:根据条形统计图可得,1+1+2+3+9=16,
14号线的中位数第11个数据在1.30≤x<1.50这一组第4个数据为1.38,
故答案为:1.38;
(2)解:选择7号线,理由如下:
7号线的客运强度的平均数及中位数均小于14号线,说明人流量较小,所以选择7号线;
(3)166天
同课章节目录
