2024年中考数学一轮复习综合练习题:圆(含解析)
文档属性
| 名称 | 2024年中考数学一轮复习综合练习题:圆(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 405.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 14:56:57 | ||
图片预览



文档简介
2024年中考数学一轮复习综合练习题:圆
一、单选题
1.用反证法证明命题:“在△ABC中,∠A,∠B的对边分别是a,b,若∠A<∠B,则aA.a>b B.a≥b C.a≤b D.a≠b
2.如图所示,点A,B,C在圆O上,∠A=64°,则∠BOC的度数是( )
A.26° B.116° C.128° D.154°
3.如图,在⊙O中,OC⊥弦AB于点C,AB=4,OC=1,则OB的长是( )
A. B. C. D.
4.如图,在 中, , , ,以点 为圆心,3为半径的圆与 所在直线的位置关系是( )
A.相交 B.相离 C.相切 D.无法判断
5.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠CDA=118°,则∠C的度数为( )
A.32° B.33° C.34° D.44°
6.平面直角坐标系中,⊙P的圆心坐标为(-4,-5),半径为5,那么⊙P与y轴的位置关系是( )
A.相交 B.相离 C.相切 D.以上都不是
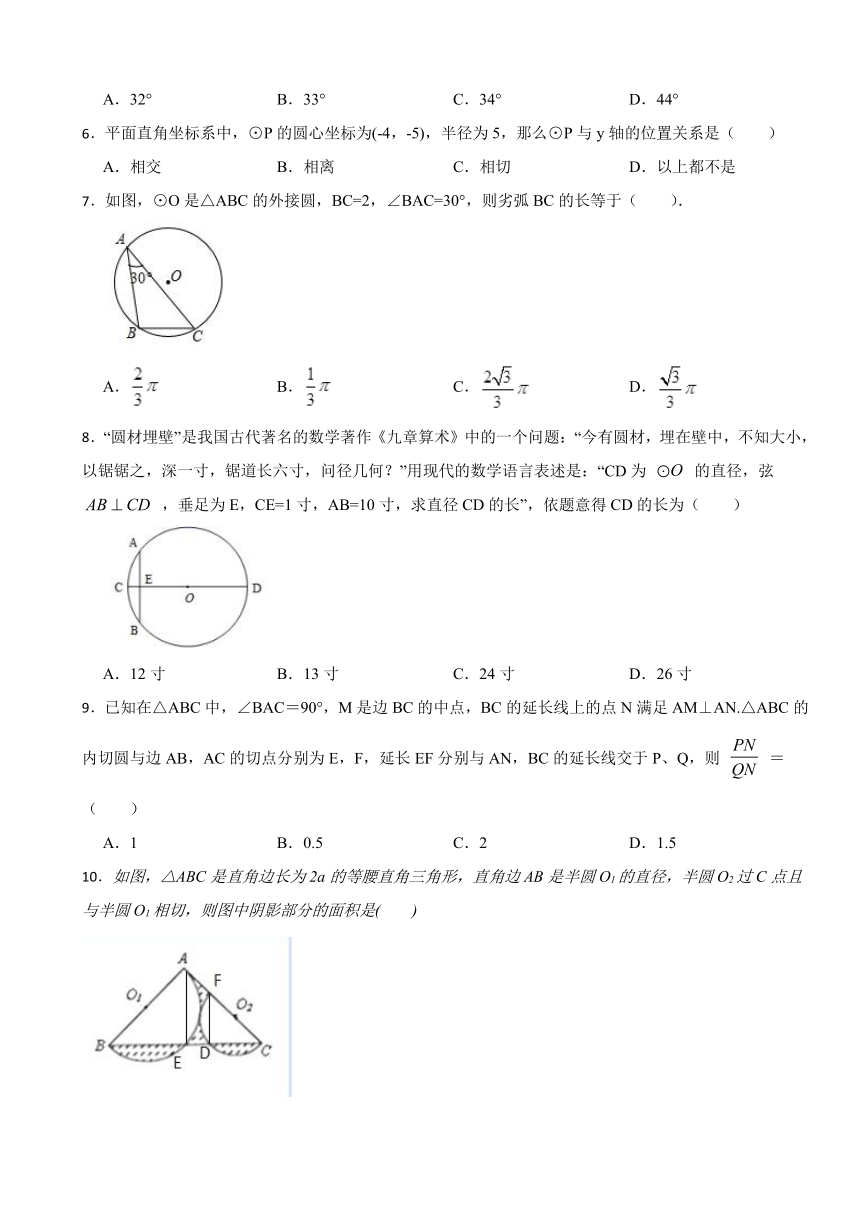
7.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧BC的长等于( ).
A. B. C. D.
8.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“CD为 的直径,弦 ,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
A.12寸 B.13寸 C.24寸 D.26寸
9.已知在△ABC中,∠BAC=90°,M是边BC的中点,BC的延长线上的点N满足AM⊥AN.△ABC的内切圆与边AB,AC的切点分别为E,F,延长EF分别与AN,BC的延长线交于P、Q,则 =( )
A.1 B.0.5 C.2 D.1.5
10.如图,△ABC是直角边长为2a的等腰直角三角形,直角边AB是半圆O1的直径,半圆O2过C点且与半圆O1相切,则图中阴影部分的面积是( )
A. B. C. D.
二、填空题
11.一个扇形的圆心角为120°,半径为3,则这个扇形的面积为 (结果保留π)
12.如图,⊙O的弦AB与半径OC相交于点P,BC∥OA,∠C=50°,那么∠APC的度数为
13.如图,为的直径,弦,垂足为,,,,则弦的长度为 .
14.如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是 上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为 .
15.如图,正六边形ABCDEF的边长是6+4 ,点O1,O2分别是△ABF,△CDE的内心,则O1O2= .
三、解答题
16.已知:如图,在⊙O中,AB=CD,AB与CD相交于点M.
求证:AM=DM.
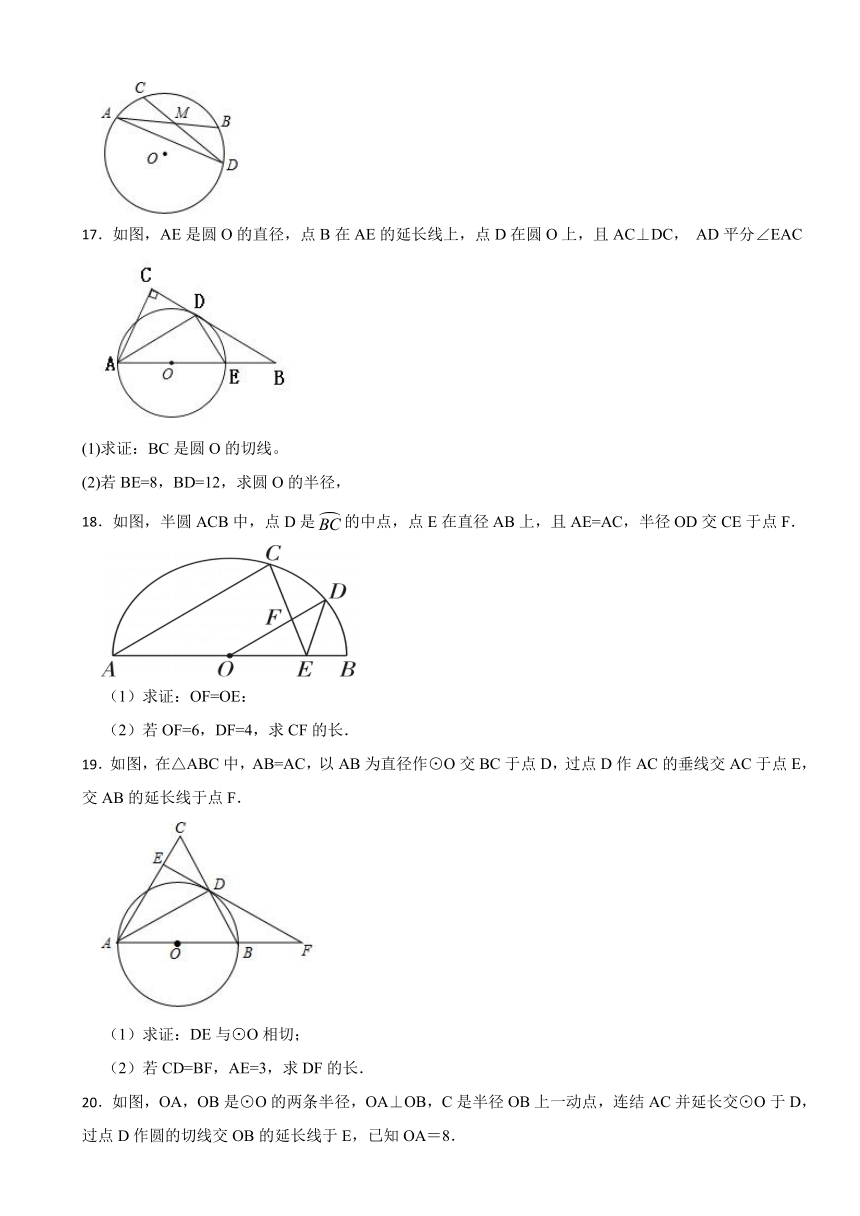
17.如图,AE是圆O的直径,点B在AE的延长线上,点D在圆O上,且AC⊥DC, AD平分∠EAC
(1)求证:BC是圆O的切线。
(2)若BE=8,BD=12,求圆O的半径,
18.如图,半圆ACB中,点D是的中点,点E在直径AB上,且AE=AC,半径OD交CE于点F.
(1)求证:OF=OE:
(2)若OF=6,DF=4,求CF的长.
19.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.
(1)求证:DE与⊙O相切;
(2)若CD=BF,AE=3,求DF的长.
20.如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
(1)求证:∠ECD=∠EDC;
(2)若tanA= ,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
答案解析部分
1.【答案】B
【解析】【解答】解:用反证法证明命题:“在△ABC中,∠A,∠B的对边分别是a,b,若∠A<∠B,则a故答案为:B.
【分析】用反证法证明的第一步为:假设结论不成立,据此判断.
2.【答案】C
【解析】【解答】圆周角定理:同弧所对的圆周角等于圆心角的一半。
故答案为:C.
【分析】根据圆周角定理可求出∠BOC的度数。
3.【答案】B
【解析】【解答】解:∵OC⊥弦AB于点C,
∴AC=BC= AB,
在Rt△OBC中,OB= = .
故选B.
【分析】根据垂径定理可得AC=BC= AB,在Rt△OBC中可求出OB.
4.【答案】A
【解析】【解答】解:过点C作CD⊥AB于点D,如图所示:
∵ , , ,
∴ ,
根据等积法可得 ,
∴ ,
∵以点 为圆心,3为半径的圆,
∴该圆的半径为3,
∵ ,
∴圆与AB所在的直线的位置关系为相交,
故答案为:A.
【分析】过点C作CD⊥AB于点D,由勾股定理可得AB的长度,根据三角形面积可得CD的长度,由圆心到直线的距离为d,圆的半径为r,根据直线和圆的位置关系,d<r,直线与圆相离,d=r,直线与圆相切,d>r,直线与圆相交判断即可.
5.【答案】C
【解析】【解答】解:如图,连接OD,
∵CD与⊙O相切于点D,
∴∠ODC=90°,
∵∠CDA=118°,
∴∠ODA=∠CDA-∠ODC=118°-90°=28°,
∵OD=OA,
∴∠OAD=∠ODA=28°,
∴∠DOC=2∠ODA=56°,
∴∠C=90°-∠DOC=34°.
故答案为:C
【分析】连接OD,先求出∠ODA=∠CDA-∠ODC=118°-90°=28°,根据等边对等角的性质可得∠OAD=∠ODA=28°,根据圆周角的性质可得∠DOC=2∠ODA=56°,再利用角的运算可得∠C=90°-∠DOC=34°。
6.【答案】A
【解析】【解答】解:∵圆P的圆心坐标为(-4,-5),
∴点P到y轴的距离为|-4|=4<5,
∴圆P与y轴相交.
故答案为:A.
【分析】利用点P的坐标,可得到点P到y轴的距离,再与5比较大小,利用点与圆的位置关系,可得答案。
7.【答案】A
【解析】【解答】 解:连结OC、OB,如图,
∵ ∠BAC=30°,
∴ ∠BOC=2∠BAC=60°,
∵OB=OC,
∴△BOC为等边三角形,
∵BC=2,
∴r=2,
∴的长为:=.
故答案为:A.
【分析】连结OC、OB,根据圆周角定理得∠BOC=60°, 由等边三角形判定得BOC为等边三角形,根据弧长公式计算即可得出答案.
8.【答案】D
【解析】【解答】解:如图,连接AO,
设直径CD的长为 寸,则半径OA=OC=x寸,
∵CD为 的直径,弦 ,垂足为E,AB=10寸,
∴AE=BE= AB=5寸,
根据勾股定理可知,
在Rt△AOE中, ,
∴ ,
解得: ,
∴ ,
即CD长为26寸.
【分析】连接AO,设直径CD的长为 寸,则半径OA=OC= 寸,然后利用垂径定理得出AE,最后根据勾股定理进一步求解即可.
9.【答案】A
【解析】【解答】取△ACB的内切圆的圆心是O,连接OE、OF,作NA的延长线AG,
则OE⊥AB,OF⊥AC,OE=OF,
∵∠BAC=90°,
∴四边形AEOF是正方形,
∴AE=AF,
∴∠AEF=∠AFE,
∵∠BAC=90°,M为斜边BC上中线,
∴AM=CM=BM,
∴∠MAC=∠MCA,
∵∠BAC=90°,AN⊥AM,
∴∠BAC=∠MAG=∠MAN=90°,
∴∠GAE+∠EAM=90°,∠EAM+∠MAC=90°,∠MAC+∠CAN=90°,
∴∠GAE=∠MAC=∠MCA,∠EAM=∠CAP,
∵∠GAE=∠APE+∠AEP,∠MCA=∠Q+∠CFQ,
∵∠AEF=∠AFE=∠CFQ,∠EPA=∠NPQ,
∴∠Q=∠NPQ,
∴PN=QN,
∴ =1,
故答案为:A.
【分析】取△ACB的内切圆的圆心是O,连接OE、OF,作NA的延长线AG,根据有一组邻边相等的矩形判断四边形AEOF是正方形,再利用正方形的性质及直角三角形斜边的中线等于斜边的一半证出∠AEF=∠AFE,∠MAC=∠MCA,由同角的余角相等可得∠GAE=∠MAC=∠MCA,∠EAM=∠CAP,再根据三角形的外角的性质∠GAE=∠APE+∠AEP,∠MCA=∠Q+∠CFQ,利用等量代换求出∠Q=∠NPQ,再由等角对等边即可求出答案.
10.【答案】D
【解析】【解答】连接O1O2设O2的半径为x.
∵O1O22-AO12=AO22,
∴(a+x)2-a 2=(2a-x)2,
解得:x=a.
设⊙O1交BC于D,⊙O2交BC于E.
∴CE=PE=x=,BC=AB,CD=AB=a,
∴S阴影=S△ADC-S△CEP=CD AD-CE PE=×a a-×a a=a2.
故选D.
【分析】利用等弦所对的弧相等,先把阴影部分变化成一个直角梯形,然后再利用等腰直角三角形求小圆的半径,从而求阴影部分的面积.本题考查了勾股定理,以及三角形的面积的计算,正确理解阴影部分的面积等于梯形PEDA的面积是关键.
11.【答案】3π
【解析】【解答】此题考查扇形面积的计算,熟记扇形面积公式 ,即可求解.
根据扇形面积公式,计算这个扇形的面积为 .
【分析】根据扇形的面积公式即可得出结果.
12.【答案】75°
【解析】【解答】解:∵BC∥OA,∠C=50°,
∴∠AOC=∠C=50°,
∴∠B=∠AOC=25°,
∴∠APC=∠B+∠C=75°.
故答案为:75°.
【分析】由BC∥OA,∠C=50°,根据平行线的性质,可求得∠AOC的度数,又由圆周角定理,可求得∠B的度数,然后由三角形外角的性质,求得答案.
13.【答案】
【解析】【解答】解:连接、,交于,如图,
∵,
,
设⊙的半径为,则,,
在中,,解得,
∵,
,,
在中,,①
在中,,②
解由①②组成的方程组得到,
.
故答案为.
【分析】连接、,交于,由垂径定理可得,设⊙的半径为,则,,在中,利用勾股定理建立关于r方程并解之,即得OA=5,由可得,,在中,①,在中,②,联立①②可得AG的长,继而得解.
14.【答案】 ﹣2
【解析】【解答】解:如图,连接BO',BC,
∵CE⊥AD,
∴∠AEC=90°,
∴在点D移动的过程中,点E在以AC为直径的圆上运动,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,∵AC=4,AB=5,
∴BC=,
在Rt△BCO′中,,
∵O′E+BE O′B,
∴当O′、E. B共线时,BE的值最小,最小值为O′B O′E=.
故答案为:.
【分析】连接BO′、BC,在点D移动的过程中,点E在以AC为直径的圆上运动,当O′、E、B共线时,BE的值最小,最小值为O′B- O′E,利用勾股定理求出B O′即可解决问题.
15.【答案】
【解析】【解答】解:如图,过A作AM⊥BF于M,连接O1F、O1A、O1B,
∵六边形ABCDEF是正六边形,
∴∠A= =120°,AF=AB,
∴∠AFB=∠ABF= ×(180°﹣120°)=30°,
∴△AFB边BF上的高AM= AF= ×(6+4 )=3+2 ,
FM=BM= AM=3 +6,
∴BF=3 +6+3 +6=12+6 ,
设△AFB的内切圆的半径为r,
∵S△AFB=
∴ ×(3+2 )×(3 +6)
= ×(6+4 )×r+ ×(6+4 )×r+ ×(12+6 )×r,
解得:r= ,
即O1M=r= ,
∴O1O2=2× +6+4 =9+4 ,
故答案为:9+4
【分析】如图,过A作AM⊥BF于M,连接O1F、O1A、O1B,根据正六边形的性质得出∠A=120°,AF=AB,根据三角形的内角和及等边对等角得出∠AFB=∠ABF=30°,根据含30 直角三角形的边之间的关系得出AM的长,FM的长,进而根据等腰三角形的三线合一得出BF的长,设△AFB的内切圆的半径为r,根据S△AFB= S△AO1F+S△AO1E+S△BFO1,建立出方程,求解得出r的值,从而得出答案。
16.【答案】证明:∵AB=CD,
∴ = ,
∴ ﹣ = ﹣ ,
∴ = ,
∴∠D=∠A,
∴MA=MD.
【解析】【分析】欲证明AM=DM,只要证明∠D=∠A即可;
17.【答案】解:(1)证明:连接OC;
∵AD平分∠EAC,
∴∠CAD=∠BAD;
又在圆中OA=OD,
∴∠AD0=∠OAD,
∴∠CAD=∠ADO,
∴AC∥OD;
则由AE⊥DC知OC⊥DC,
即DC是⊙O的切线.
(2)解:∵∠B=∠B,∠DAE=∠BDE,
∴△BDE∽△BAE,
∴,
∴BD2=BE·BA,
即:BD2=BE·(BE+EA),
∴122=8(8+AE)
∴AE=10.
【解析】【分析】(1)要证DE是⊙O的切线,只要连接OC,再证∠DCO=90°即可.
(2)已知两边长,求其它边的长,可以来三角形相似,对应边成比例来求.
18.【答案】(1)证明:连接BC,交OD于点G
∵AB是半圆O的直径
∴∠ACB= 90°
∴AC⊥BC
∵D是BC的中点,OD是半径
∴OD⊥BC
∴OD∥AC
∴∠OFE=∠ACE
∵AE=AC
∴∠OEF=∠ACE
∴∠OFE=∠OEF
∴OF=OE;
(2)解:若OF=6,DF=4,则OE=OF=6,OA=OB=OD=OF+DF=10
∴AC=AE=AO+OE=16,AB=20
在Rt△ACB中,BC==12
∵OD是半径且OD⊥BC
∴BG=CG=6
在Rt△OBG中,OG==8
∴FG=OG-OF= 2
∴在Rt△CFG中,CF=-
【解析】【分析】(1)利用圆周角定理和垂径定理得AC⊥BC、OD⊥BC,由同一平面内垂直同一直线的两条直线互相平行得OD∥AC,再通过平行线的性质证得∠OFE=∠ACE,然后由AE=AC证得∠OEF=∠ACE=∠OFE,进而得到OF=OE;
(2)通过线段的等量关系得到AB、AC的长度,再利用勾股定理计算出BC的长度,接着通过垂径定理求得OG的长度后,得到FG长,然后利用勾股定理计算出CF的长度.
19.【答案】(1)证明:连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
又∵AB=AC,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠ADO,
∴∠1=∠ADO,
∴OD∥AC,
∵DE⊥AC,
∴∠ODF=∠AED=90°,
∴OD⊥ED,
∵OD过0,
∴DE与⊙O相切.
(2)解:∵AB=AC,AD⊥BC,
∴∠1=∠2,CD=BD,
∵CD=BF,
∴BF=BD,
∴∠3=∠F,
∴∠4=∠3+∠F=2∠3,
∵OB=OD,
∴∠ODB=∠4=2∠3,
∵∠ODF=90°,
∴∠3=∠F=30°,∠4=∠ODB=60°,
∵∠ADB=90°,
∴∠2=∠1=30°,
∴∠2=∠F,
∴DF=AD,
∵∠1=30°,∠AED=90°,
∴AD=2ED,
∵AE2+DE2=AD2,AE=3,
∴AD=2 ,
∴DF=2 .
【解析】【分析】(1)连接OD,利用OD=AO,得到 ∠1=∠ADO, 进而得到OD平行AC,结合垂直关系和切线的判定,即可得出答案。
(2)根据等腰三角形的三线重合可知CD=BD,结合条件又知BD=BF,从而有∠3=∠F=30° ,进而得到 ∠2=∠1=30°,故DF=AD,AD=2ED,在Rt△AED中利用30°的性质计算边长AD,即可得出答案。
20.【答案】(1)证明:连结OD, ∵DE是⊙O的切线,∴∠EDC+∠ODA=90°, 又∵OA⊥OB,∴∠ACO+∠A=90°,
∵OA=OD,∴∠ODA=∠A,∴∠EDC=∠ACO,
又∵∠ECD=∠ACO,∴∠ECD=∠EDC.
(2)解:∵tanA= ,∴ ,∴OC=2, 设DE=x,∵∠ECD=∠EDC,∴CE=x,∴OE=2+x.
∵∠ODE=90°,∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,∴DE=CE=15.
(3)解:过点D作AO的垂线,交AO的延长于F, 当 时,则 ,DF=4,
当 时, ,DF=4 ,
,
【解析】【分析】(1)运用切线的性质以及对顶角相等,角的等量代换可证得;(2)由tanA= ,可解出OC,由(1)得∠ECD=∠EDC,等角对等边,则EC=DE,由勾股定理得OD2+DE2=OE2,构造方程解出DE的长;(3)分别求出 和 时,弓形ABD的面积,再用前者减去后者即可得到答案.
一、单选题
1.用反证法证明命题:“在△ABC中,∠A,∠B的对边分别是a,b,若∠A<∠B,则a
2.如图所示,点A,B,C在圆O上,∠A=64°,则∠BOC的度数是( )
A.26° B.116° C.128° D.154°
3.如图,在⊙O中,OC⊥弦AB于点C,AB=4,OC=1,则OB的长是( )
A. B. C. D.
4.如图,在 中, , , ,以点 为圆心,3为半径的圆与 所在直线的位置关系是( )
A.相交 B.相离 C.相切 D.无法判断
5.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠CDA=118°,则∠C的度数为( )
A.32° B.33° C.34° D.44°
6.平面直角坐标系中,⊙P的圆心坐标为(-4,-5),半径为5,那么⊙P与y轴的位置关系是( )
A.相交 B.相离 C.相切 D.以上都不是
7.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧BC的长等于( ).
A. B. C. D.
8.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“CD为 的直径,弦 ,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
A.12寸 B.13寸 C.24寸 D.26寸
9.已知在△ABC中,∠BAC=90°,M是边BC的中点,BC的延长线上的点N满足AM⊥AN.△ABC的内切圆与边AB,AC的切点分别为E,F,延长EF分别与AN,BC的延长线交于P、Q,则 =( )
A.1 B.0.5 C.2 D.1.5
10.如图,△ABC是直角边长为2a的等腰直角三角形,直角边AB是半圆O1的直径,半圆O2过C点且与半圆O1相切,则图中阴影部分的面积是( )
A. B. C. D.
二、填空题
11.一个扇形的圆心角为120°,半径为3,则这个扇形的面积为 (结果保留π)
12.如图,⊙O的弦AB与半径OC相交于点P,BC∥OA,∠C=50°,那么∠APC的度数为
13.如图,为的直径,弦,垂足为,,,,则弦的长度为 .
14.如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是 上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为 .
15.如图,正六边形ABCDEF的边长是6+4 ,点O1,O2分别是△ABF,△CDE的内心,则O1O2= .
三、解答题
16.已知:如图,在⊙O中,AB=CD,AB与CD相交于点M.
求证:AM=DM.
17.如图,AE是圆O的直径,点B在AE的延长线上,点D在圆O上,且AC⊥DC, AD平分∠EAC
(1)求证:BC是圆O的切线。
(2)若BE=8,BD=12,求圆O的半径,
18.如图,半圆ACB中,点D是的中点,点E在直径AB上,且AE=AC,半径OD交CE于点F.
(1)求证:OF=OE:
(2)若OF=6,DF=4,求CF的长.
19.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.
(1)求证:DE与⊙O相切;
(2)若CD=BF,AE=3,求DF的长.
20.如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
(1)求证:∠ECD=∠EDC;
(2)若tanA= ,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
答案解析部分
1.【答案】B
【解析】【解答】解:用反证法证明命题:“在△ABC中,∠A,∠B的对边分别是a,b,若∠A<∠B,则a
【分析】用反证法证明的第一步为:假设结论不成立,据此判断.
2.【答案】C
【解析】【解答】圆周角定理:同弧所对的圆周角等于圆心角的一半。
故答案为:C.
【分析】根据圆周角定理可求出∠BOC的度数。
3.【答案】B
【解析】【解答】解:∵OC⊥弦AB于点C,
∴AC=BC= AB,
在Rt△OBC中,OB= = .
故选B.
【分析】根据垂径定理可得AC=BC= AB,在Rt△OBC中可求出OB.
4.【答案】A
【解析】【解答】解:过点C作CD⊥AB于点D,如图所示:
∵ , , ,
∴ ,
根据等积法可得 ,
∴ ,
∵以点 为圆心,3为半径的圆,
∴该圆的半径为3,
∵ ,
∴圆与AB所在的直线的位置关系为相交,
故答案为:A.
【分析】过点C作CD⊥AB于点D,由勾股定理可得AB的长度,根据三角形面积可得CD的长度,由圆心到直线的距离为d,圆的半径为r,根据直线和圆的位置关系,d<r,直线与圆相离,d=r,直线与圆相切,d>r,直线与圆相交判断即可.
5.【答案】C
【解析】【解答】解:如图,连接OD,
∵CD与⊙O相切于点D,
∴∠ODC=90°,
∵∠CDA=118°,
∴∠ODA=∠CDA-∠ODC=118°-90°=28°,
∵OD=OA,
∴∠OAD=∠ODA=28°,
∴∠DOC=2∠ODA=56°,
∴∠C=90°-∠DOC=34°.
故答案为:C
【分析】连接OD,先求出∠ODA=∠CDA-∠ODC=118°-90°=28°,根据等边对等角的性质可得∠OAD=∠ODA=28°,根据圆周角的性质可得∠DOC=2∠ODA=56°,再利用角的运算可得∠C=90°-∠DOC=34°。
6.【答案】A
【解析】【解答】解:∵圆P的圆心坐标为(-4,-5),
∴点P到y轴的距离为|-4|=4<5,
∴圆P与y轴相交.
故答案为:A.
【分析】利用点P的坐标,可得到点P到y轴的距离,再与5比较大小,利用点与圆的位置关系,可得答案。
7.【答案】A
【解析】【解答】 解:连结OC、OB,如图,
∵ ∠BAC=30°,
∴ ∠BOC=2∠BAC=60°,
∵OB=OC,
∴△BOC为等边三角形,
∵BC=2,
∴r=2,
∴的长为:=.
故答案为:A.
【分析】连结OC、OB,根据圆周角定理得∠BOC=60°, 由等边三角形判定得BOC为等边三角形,根据弧长公式计算即可得出答案.
8.【答案】D
【解析】【解答】解:如图,连接AO,
设直径CD的长为 寸,则半径OA=OC=x寸,
∵CD为 的直径,弦 ,垂足为E,AB=10寸,
∴AE=BE= AB=5寸,
根据勾股定理可知,
在Rt△AOE中, ,
∴ ,
解得: ,
∴ ,
即CD长为26寸.
【分析】连接AO,设直径CD的长为 寸,则半径OA=OC= 寸,然后利用垂径定理得出AE,最后根据勾股定理进一步求解即可.
9.【答案】A
【解析】【解答】取△ACB的内切圆的圆心是O,连接OE、OF,作NA的延长线AG,
则OE⊥AB,OF⊥AC,OE=OF,
∵∠BAC=90°,
∴四边形AEOF是正方形,
∴AE=AF,
∴∠AEF=∠AFE,
∵∠BAC=90°,M为斜边BC上中线,
∴AM=CM=BM,
∴∠MAC=∠MCA,
∵∠BAC=90°,AN⊥AM,
∴∠BAC=∠MAG=∠MAN=90°,
∴∠GAE+∠EAM=90°,∠EAM+∠MAC=90°,∠MAC+∠CAN=90°,
∴∠GAE=∠MAC=∠MCA,∠EAM=∠CAP,
∵∠GAE=∠APE+∠AEP,∠MCA=∠Q+∠CFQ,
∵∠AEF=∠AFE=∠CFQ,∠EPA=∠NPQ,
∴∠Q=∠NPQ,
∴PN=QN,
∴ =1,
故答案为:A.
【分析】取△ACB的内切圆的圆心是O,连接OE、OF,作NA的延长线AG,根据有一组邻边相等的矩形判断四边形AEOF是正方形,再利用正方形的性质及直角三角形斜边的中线等于斜边的一半证出∠AEF=∠AFE,∠MAC=∠MCA,由同角的余角相等可得∠GAE=∠MAC=∠MCA,∠EAM=∠CAP,再根据三角形的外角的性质∠GAE=∠APE+∠AEP,∠MCA=∠Q+∠CFQ,利用等量代换求出∠Q=∠NPQ,再由等角对等边即可求出答案.
10.【答案】D
【解析】【解答】连接O1O2设O2的半径为x.
∵O1O22-AO12=AO22,
∴(a+x)2-a 2=(2a-x)2,
解得:x=a.
设⊙O1交BC于D,⊙O2交BC于E.
∴CE=PE=x=,BC=AB,CD=AB=a,
∴S阴影=S△ADC-S△CEP=CD AD-CE PE=×a a-×a a=a2.
故选D.
【分析】利用等弦所对的弧相等,先把阴影部分变化成一个直角梯形,然后再利用等腰直角三角形求小圆的半径,从而求阴影部分的面积.本题考查了勾股定理,以及三角形的面积的计算,正确理解阴影部分的面积等于梯形PEDA的面积是关键.
11.【答案】3π
【解析】【解答】此题考查扇形面积的计算,熟记扇形面积公式 ,即可求解.
根据扇形面积公式,计算这个扇形的面积为 .
【分析】根据扇形的面积公式即可得出结果.
12.【答案】75°
【解析】【解答】解:∵BC∥OA,∠C=50°,
∴∠AOC=∠C=50°,
∴∠B=∠AOC=25°,
∴∠APC=∠B+∠C=75°.
故答案为:75°.
【分析】由BC∥OA,∠C=50°,根据平行线的性质,可求得∠AOC的度数,又由圆周角定理,可求得∠B的度数,然后由三角形外角的性质,求得答案.
13.【答案】
【解析】【解答】解:连接、,交于,如图,
∵,
,
设⊙的半径为,则,,
在中,,解得,
∵,
,,
在中,,①
在中,,②
解由①②组成的方程组得到,
.
故答案为.
【分析】连接、,交于,由垂径定理可得,设⊙的半径为,则,,在中,利用勾股定理建立关于r方程并解之,即得OA=5,由可得,,在中,①,在中,②,联立①②可得AG的长,继而得解.
14.【答案】 ﹣2
【解析】【解答】解:如图,连接BO',BC,
∵CE⊥AD,
∴∠AEC=90°,
∴在点D移动的过程中,点E在以AC为直径的圆上运动,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,∵AC=4,AB=5,
∴BC=,
在Rt△BCO′中,,
∵O′E+BE O′B,
∴当O′、E. B共线时,BE的值最小,最小值为O′B O′E=.
故答案为:.
【分析】连接BO′、BC,在点D移动的过程中,点E在以AC为直径的圆上运动,当O′、E、B共线时,BE的值最小,最小值为O′B- O′E,利用勾股定理求出B O′即可解决问题.
15.【答案】
【解析】【解答】解:如图,过A作AM⊥BF于M,连接O1F、O1A、O1B,
∵六边形ABCDEF是正六边形,
∴∠A= =120°,AF=AB,
∴∠AFB=∠ABF= ×(180°﹣120°)=30°,
∴△AFB边BF上的高AM= AF= ×(6+4 )=3+2 ,
FM=BM= AM=3 +6,
∴BF=3 +6+3 +6=12+6 ,
设△AFB的内切圆的半径为r,
∵S△AFB=
∴ ×(3+2 )×(3 +6)
= ×(6+4 )×r+ ×(6+4 )×r+ ×(12+6 )×r,
解得:r= ,
即O1M=r= ,
∴O1O2=2× +6+4 =9+4 ,
故答案为:9+4
【分析】如图,过A作AM⊥BF于M,连接O1F、O1A、O1B,根据正六边形的性质得出∠A=120°,AF=AB,根据三角形的内角和及等边对等角得出∠AFB=∠ABF=30°,根据含30 直角三角形的边之间的关系得出AM的长,FM的长,进而根据等腰三角形的三线合一得出BF的长,设△AFB的内切圆的半径为r,根据S△AFB= S△AO1F+S△AO1E+S△BFO1,建立出方程,求解得出r的值,从而得出答案。
16.【答案】证明:∵AB=CD,
∴ = ,
∴ ﹣ = ﹣ ,
∴ = ,
∴∠D=∠A,
∴MA=MD.
【解析】【分析】欲证明AM=DM,只要证明∠D=∠A即可;
17.【答案】解:(1)证明:连接OC;
∵AD平分∠EAC,
∴∠CAD=∠BAD;
又在圆中OA=OD,
∴∠AD0=∠OAD,
∴∠CAD=∠ADO,
∴AC∥OD;
则由AE⊥DC知OC⊥DC,
即DC是⊙O的切线.
(2)解:∵∠B=∠B,∠DAE=∠BDE,
∴△BDE∽△BAE,
∴,
∴BD2=BE·BA,
即:BD2=BE·(BE+EA),
∴122=8(8+AE)
∴AE=10.
【解析】【分析】(1)要证DE是⊙O的切线,只要连接OC,再证∠DCO=90°即可.
(2)已知两边长,求其它边的长,可以来三角形相似,对应边成比例来求.
18.【答案】(1)证明:连接BC,交OD于点G
∵AB是半圆O的直径
∴∠ACB= 90°
∴AC⊥BC
∵D是BC的中点,OD是半径
∴OD⊥BC
∴OD∥AC
∴∠OFE=∠ACE
∵AE=AC
∴∠OEF=∠ACE
∴∠OFE=∠OEF
∴OF=OE;
(2)解:若OF=6,DF=4,则OE=OF=6,OA=OB=OD=OF+DF=10
∴AC=AE=AO+OE=16,AB=20
在Rt△ACB中,BC==12
∵OD是半径且OD⊥BC
∴BG=CG=6
在Rt△OBG中,OG==8
∴FG=OG-OF= 2
∴在Rt△CFG中,CF=-
【解析】【分析】(1)利用圆周角定理和垂径定理得AC⊥BC、OD⊥BC,由同一平面内垂直同一直线的两条直线互相平行得OD∥AC,再通过平行线的性质证得∠OFE=∠ACE,然后由AE=AC证得∠OEF=∠ACE=∠OFE,进而得到OF=OE;
(2)通过线段的等量关系得到AB、AC的长度,再利用勾股定理计算出BC的长度,接着通过垂径定理求得OG的长度后,得到FG长,然后利用勾股定理计算出CF的长度.
19.【答案】(1)证明:连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
又∵AB=AC,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠ADO,
∴∠1=∠ADO,
∴OD∥AC,
∵DE⊥AC,
∴∠ODF=∠AED=90°,
∴OD⊥ED,
∵OD过0,
∴DE与⊙O相切.
(2)解:∵AB=AC,AD⊥BC,
∴∠1=∠2,CD=BD,
∵CD=BF,
∴BF=BD,
∴∠3=∠F,
∴∠4=∠3+∠F=2∠3,
∵OB=OD,
∴∠ODB=∠4=2∠3,
∵∠ODF=90°,
∴∠3=∠F=30°,∠4=∠ODB=60°,
∵∠ADB=90°,
∴∠2=∠1=30°,
∴∠2=∠F,
∴DF=AD,
∵∠1=30°,∠AED=90°,
∴AD=2ED,
∵AE2+DE2=AD2,AE=3,
∴AD=2 ,
∴DF=2 .
【解析】【分析】(1)连接OD,利用OD=AO,得到 ∠1=∠ADO, 进而得到OD平行AC,结合垂直关系和切线的判定,即可得出答案。
(2)根据等腰三角形的三线重合可知CD=BD,结合条件又知BD=BF,从而有∠3=∠F=30° ,进而得到 ∠2=∠1=30°,故DF=AD,AD=2ED,在Rt△AED中利用30°的性质计算边长AD,即可得出答案。
20.【答案】(1)证明:连结OD, ∵DE是⊙O的切线,∴∠EDC+∠ODA=90°, 又∵OA⊥OB,∴∠ACO+∠A=90°,
∵OA=OD,∴∠ODA=∠A,∴∠EDC=∠ACO,
又∵∠ECD=∠ACO,∴∠ECD=∠EDC.
(2)解:∵tanA= ,∴ ,∴OC=2, 设DE=x,∵∠ECD=∠EDC,∴CE=x,∴OE=2+x.
∵∠ODE=90°,∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,∴DE=CE=15.
(3)解:过点D作AO的垂线,交AO的延长于F, 当 时,则 ,DF=4,
当 时, ,DF=4 ,
,
【解析】【分析】(1)运用切线的性质以及对顶角相等,角的等量代换可证得;(2)由tanA= ,可解出OC,由(1)得∠ECD=∠EDC,等角对等边,则EC=DE,由勾股定理得OD2+DE2=OE2,构造方程解出DE的长;(3)分别求出 和 时,弓形ABD的面积,再用前者减去后者即可得到答案.
同课章节目录
