2024年中考数学一轮专题练习题:相似(含答案)
文档属性
| 名称 | 2024年中考数学一轮专题练习题:相似(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 205.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 15:00:16 | ||
图片预览


文档简介
2024年中考数学一轮专题练习题:相似
一、单选题
1.已知 , , ,则 与 的面积之比为( )
A. B. C. D.
2.在△ABC中,点D、E分别在边AB、AC上,联结DE,那么下列条件中不能判断△ADE和△ABC相似的是( )
A.DE∥BC B.∠AED=∠B
C.AE:AD=AB:AC D.AE:DE=AC:BC
3.如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( )
A.1 B.2 C.3 D.4
4.如图,E是矩形ABCD的边CD上的点,BE交AC于O,已知 与 的面积分别为2和8,则四边形AOED的面积为( )
A.16 B.32 C.38 D.40
5.如图,线段 两个端点的坐标分别为 、 ,以原点为位似中心,将线段 放大得到线段 ,若点 的坐标为 ,则点 的坐标为( )
A. B. C. D.
6.如图,直线 ,直线AC分别交 , , 于点A,B,C,直线DF分别交 , , 于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则 的值为( )
A. B.2 C. D.
7.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 ,那么点B′的坐标是( )
A.(-2,3) B.(2,-3)
C.(3,-2)或(-2,3) D.(-2,3)或(2,-3)
8.两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P是线段AB上一点(AP>BP),若满足,则称点P是AB的黄金分割点,世界上最有名的建筑物中几乎都包含“黄金分割”,若图中AB=8,则BP的长度是( )
A. B. C. D.2
二、填空题
9.如图,在Rt△ABC中,∠A=30°,D是斜边AB的中点,G是Rt△ABC的重心,GE⊥AC于点E.若BC=6 cm,则GE= cm.
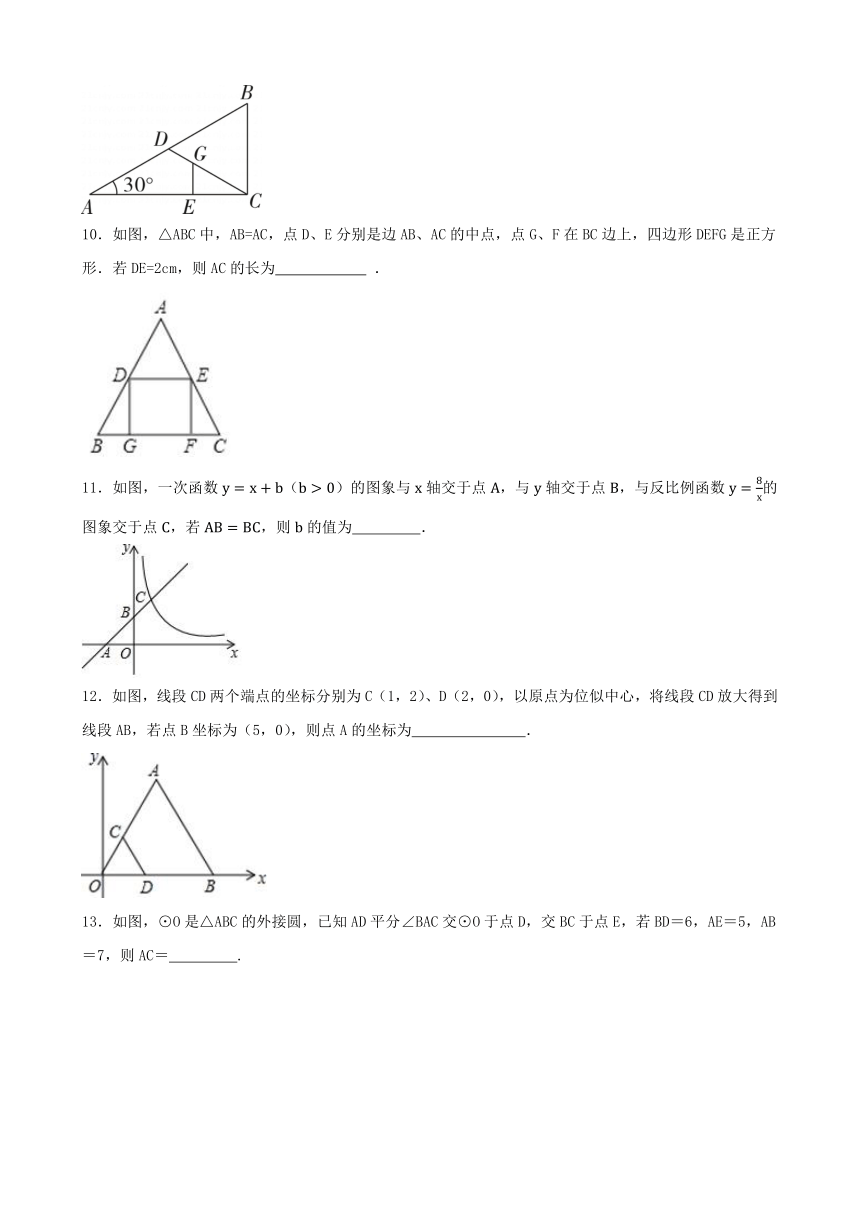
10.如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为 .
11.如图,一次函数()的图象与轴交于点,与轴交于点,与反比例函数的图象交于点,若,则的值为 .
12.如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为 .
13.如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,交BC于点E,若BD=6,AE=5,AB=7,则AC= .
三、解答题
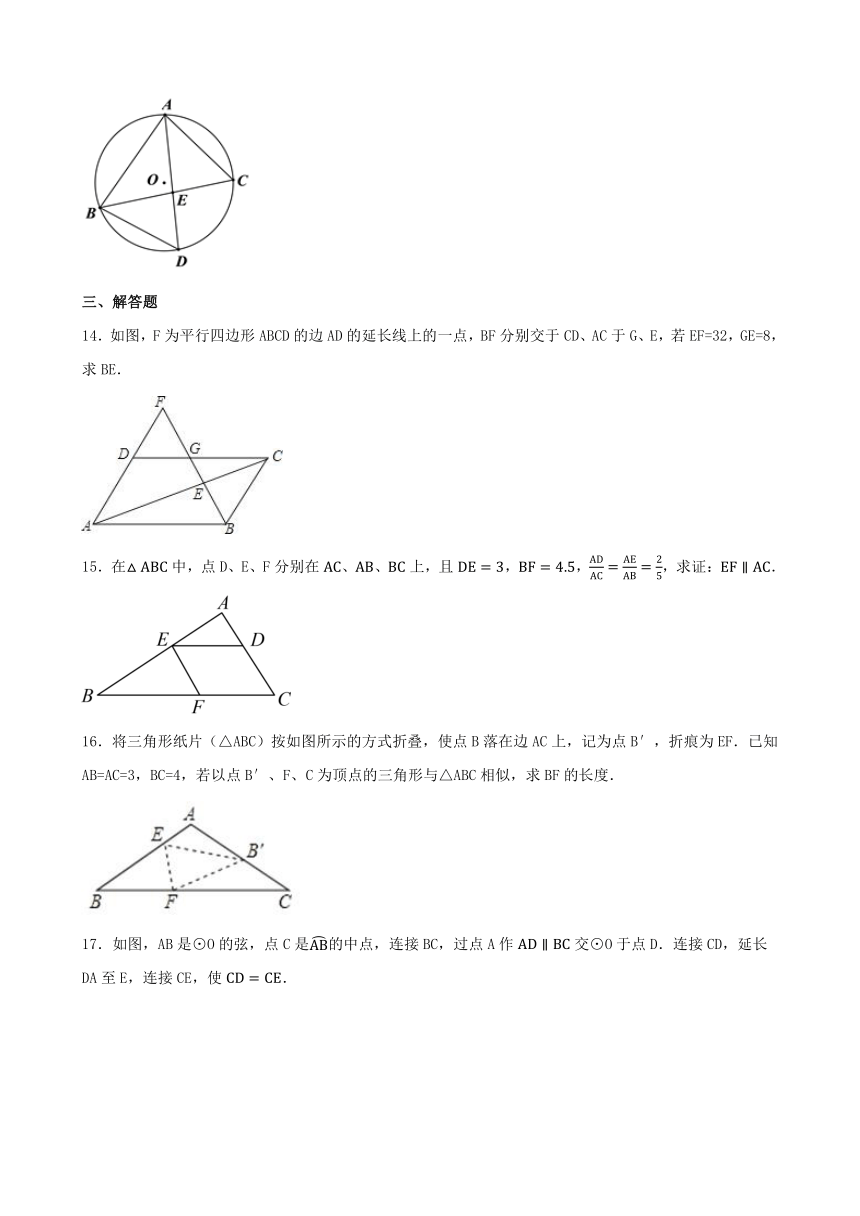
14.如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE.
15.在中,点D、E、F分别在、、上,且,,,求证:.
16.将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′、F、C为顶点的三角形与△ABC相似,求BF的长度.
17.如图,AB是⊙O的弦,点C是的中点,连接BC,过点A作交⊙O于点D.连接CD,延长DA至E,连接CE,使.
(1)求证:CE是⊙O的切线;
(2)若,,求AD的长.
18.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且 .
(1)求证:△ADF∽△ACG;
(2)若 ,求 的值.
答案
1.C
2.D
3.B
4.C
5.B
6.D
7.D
8.A
9.2
10.cm
11.2
12.(2.5,5)
13.
14.解答: 设BE=x,
∵EF=32,GE=8,
∴ FG=32-8=24,
∵平行四边形ABCD
∴AD∥BC,
∴△AFE∽△CBE,
∴,
则
∵DG∥AB,
∴△DFG∽△CBG,
∴
则 ,
则
解得:x=±16(负数舍去),
故BE=16.
15.证明:,,
,
,,
,
,
,
,
,
又,
四边形是平行四边形,
,即.
16.解:设BF=x,则CF=4﹣x,由翻折的性质得B′F=BF=x,当△B′FC∽△ABC,∴即解得x=,即BF=.当△FB′C∽△ABC,∴即,解得:x=2.∴BF的长度为:2或.
17.(1)证明:连接OC,如图所示:
∵,OC过圆心,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵OC为半径,
∴CE是⊙O的切线
(2)解:连接AC,如图所示:
∵,,
∴四边形AECB是平行四边形,,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴△CDE∽△ACE,
∴,
∵,,
∴,
∴
18.(1)证明:∵∠AED=∠B,∠DAE=∠DAE,
∴∠ADF=∠C,
∵ ,
∴△ADF∽△ACG
(2)解:∵△ADF∽△ACG,
∴ = ,
又∵ ,
∴ = ,
∴ =1
一、单选题
1.已知 , , ,则 与 的面积之比为( )
A. B. C. D.
2.在△ABC中,点D、E分别在边AB、AC上,联结DE,那么下列条件中不能判断△ADE和△ABC相似的是( )
A.DE∥BC B.∠AED=∠B
C.AE:AD=AB:AC D.AE:DE=AC:BC
3.如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( )
A.1 B.2 C.3 D.4
4.如图,E是矩形ABCD的边CD上的点,BE交AC于O,已知 与 的面积分别为2和8,则四边形AOED的面积为( )
A.16 B.32 C.38 D.40
5.如图,线段 两个端点的坐标分别为 、 ,以原点为位似中心,将线段 放大得到线段 ,若点 的坐标为 ,则点 的坐标为( )
A. B. C. D.
6.如图,直线 ,直线AC分别交 , , 于点A,B,C,直线DF分别交 , , 于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则 的值为( )
A. B.2 C. D.
7.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 ,那么点B′的坐标是( )
A.(-2,3) B.(2,-3)
C.(3,-2)或(-2,3) D.(-2,3)或(2,-3)
8.两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P是线段AB上一点(AP>BP),若满足,则称点P是AB的黄金分割点,世界上最有名的建筑物中几乎都包含“黄金分割”,若图中AB=8,则BP的长度是( )
A. B. C. D.2
二、填空题
9.如图,在Rt△ABC中,∠A=30°,D是斜边AB的中点,G是Rt△ABC的重心,GE⊥AC于点E.若BC=6 cm,则GE= cm.
10.如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为 .
11.如图,一次函数()的图象与轴交于点,与轴交于点,与反比例函数的图象交于点,若,则的值为 .
12.如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为 .
13.如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,交BC于点E,若BD=6,AE=5,AB=7,则AC= .
三、解答题
14.如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE.
15.在中,点D、E、F分别在、、上,且,,,求证:.
16.将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′、F、C为顶点的三角形与△ABC相似,求BF的长度.
17.如图,AB是⊙O的弦,点C是的中点,连接BC,过点A作交⊙O于点D.连接CD,延长DA至E,连接CE,使.
(1)求证:CE是⊙O的切线;
(2)若,,求AD的长.
18.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且 .
(1)求证:△ADF∽△ACG;
(2)若 ,求 的值.
答案
1.C
2.D
3.B
4.C
5.B
6.D
7.D
8.A
9.2
10.cm
11.2
12.(2.5,5)
13.
14.解答: 设BE=x,
∵EF=32,GE=8,
∴ FG=32-8=24,
∵平行四边形ABCD
∴AD∥BC,
∴△AFE∽△CBE,
∴,
则
∵DG∥AB,
∴△DFG∽△CBG,
∴
则 ,
则
解得:x=±16(负数舍去),
故BE=16.
15.证明:,,
,
,,
,
,
,
,
,
又,
四边形是平行四边形,
,即.
16.解:设BF=x,则CF=4﹣x,由翻折的性质得B′F=BF=x,当△B′FC∽△ABC,∴即解得x=,即BF=.当△FB′C∽△ABC,∴即,解得:x=2.∴BF的长度为:2或.
17.(1)证明:连接OC,如图所示:
∵,OC过圆心,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵OC为半径,
∴CE是⊙O的切线
(2)解:连接AC,如图所示:
∵,,
∴四边形AECB是平行四边形,,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴△CDE∽△ACE,
∴,
∵,,
∴,
∴
18.(1)证明:∵∠AED=∠B,∠DAE=∠DAE,
∴∠ADF=∠C,
∵ ,
∴△ADF∽△ACG
(2)解:∵△ADF∽△ACG,
∴ = ,
又∵ ,
∴ = ,
∴ =1
同课章节目录
