2024年中考一轮专题复习——弧长及扇形的面积(含答案)
文档属性
| 名称 | 2024年中考一轮专题复习——弧长及扇形的面积(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 317.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 15:40:17 | ||
图片预览


文档简介
2024年中考一轮专题复习——弧长及扇形的面积
一、单选题
1.已知半径为5的⊙O是△ABC的外接圆.若∠ABC=25°,则劣弧 的长为( )
A. B. C. D.
2.如图,在圆中半径OC弦AB,且弦AB=CO=2,则图中阴影部分面积为( )
A. B. C. D.
3.如图,在 ABCD中AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则的长为( )
A.
B.
C.
D.2
4.如图,在中,,,将绕点逆时针旋转后,到,点经过的路径为弧,已知,则图中阴影部分的面积为( ).
A.π B.π C.π D.π
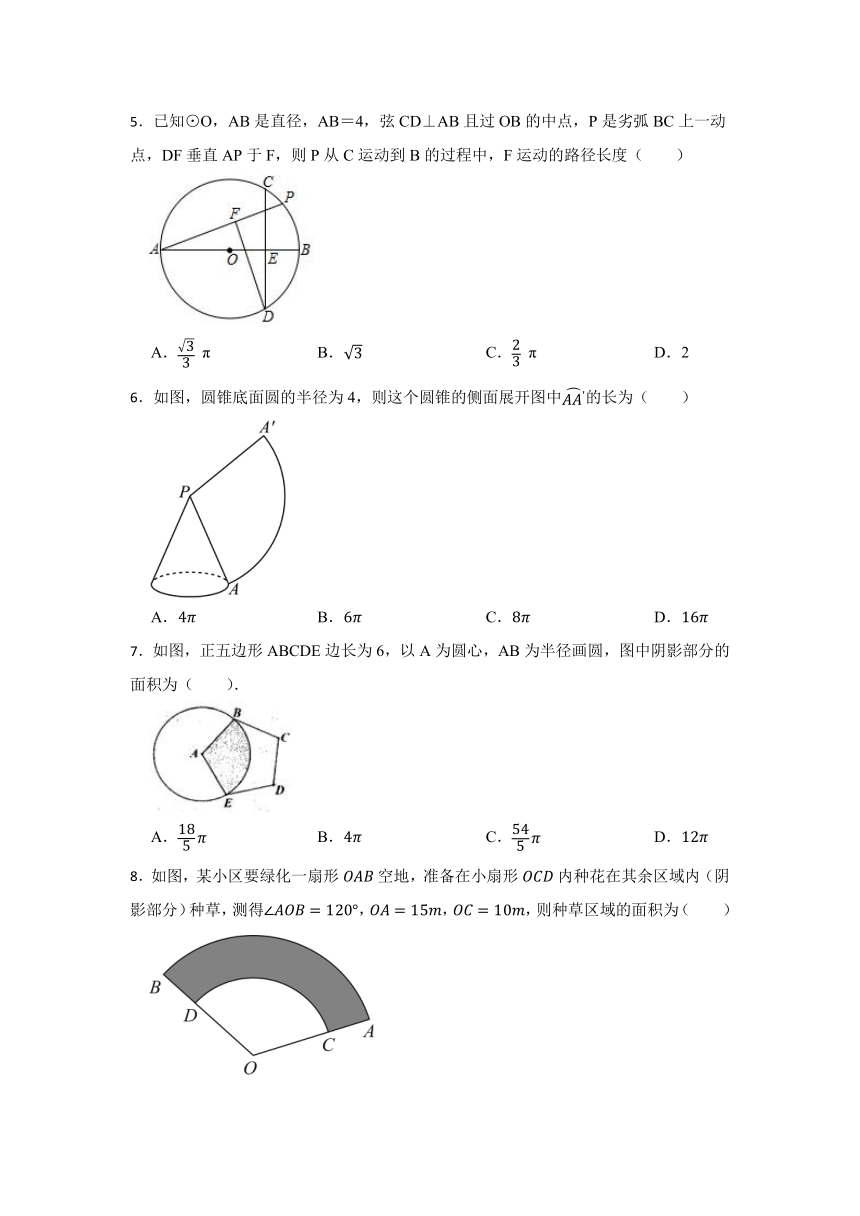
5.已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
A. π B. C. π D.2
6.如图,圆锥底面圆的半径为4,则这个圆锥的侧面展开图中的长为( )
A. B. C. D.
7.如图,正五边形ABCDE边长为6,以A为圆心,AB为半径画圆,图中阴影部分的面积为( ).
A. B. C. D.
8.如图,某小区要绿化一扇形空地,准备在小扇形内种花在其余区域内(阴影部分)种草,测得,,,则种草区域的面积为( )
A. B. C. D.
二、填空题
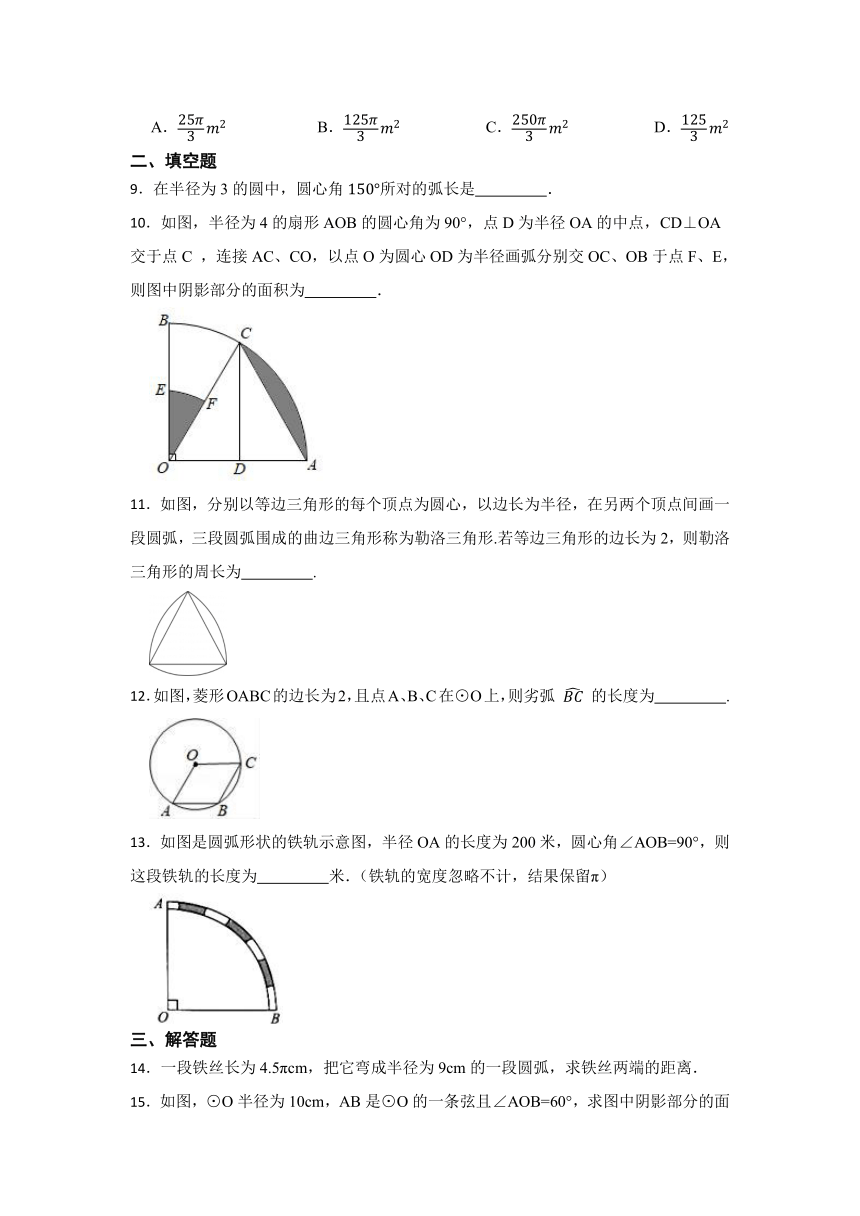
9.在半径为3的圆中,圆心角所对的弧长是 .
10.如图,半径为4的扇形AOB的圆心角为90°,点D为半径OA的中点,CD⊥OA交于点C ,连接AC、CO,以点O为圆心OD为半径画弧分别交OC、OB于点F、E,则图中阴影部分的面积为 .
11.如图,分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为2,则勒洛三角形的周长为 .
12.如图,菱形OABC的边长为2,且点A、B、C在⊙O上,则劣弧 的长度为 .
13.如图是圆弧形状的铁轨示意图,半径OA的长度为200米,圆心角∠AOB=90°,则这段铁轨的长度为 米.(铁轨的宽度忽略不计,结果保留π)
三、解答题
14.一段铁丝长为4.5πcm,把它弯成半径为9cm的一段圆弧,求铁丝两端的距离.
15.如图,⊙O半径为10cm,AB是⊙O的一条弦且∠AOB=60°,求图中阴影部分的面积.
16.如图,以为直径的经过的中点,于点.
(1)求证:是的切线;
(2)当,时,求图中阴影部分的面积结果保留根号和.
17.如图所示,已知AB是的直径,C,D是上的点,交AD于点,连结BC.
(1)求证:AE=ED.
(2)若AB=10,∠CBD=36°,求的长.
18.如图所示的益智玩具由一块主板AB和一个支撑架CD组成,其侧面示意图如图1所示,测得AB⊥BD,AB=40cm,CD=25cm,点C为AB的中点.现为了方便儿童操作,需调整玩具的摆放,将AB绕点B顺时针旋转,CD绕点C旋转,同时点D做水平滑动(如图2),当点C1到BD的距离为10cm时停止运动,求点A经过的路径的长和点D滑动的距离.(结果保留整数,参考数据: ≈1.732, ≈4.583,π≈3.142)
答案
1.C
2.C
3.C
4.C
5.A
6.C
7.C
8.B
9.
10.
11.2π
12. π
13.100π
14.解:设弯成的圆弧所对的圆心角为n° ,
则有4.5π= ,
解得n=90°,
即圆心角为直角.
由勾股定理,求得铁丝两端间的距离为 (cm).
15.解:如图,作 于点C.
由圆的基本性质可知 ,
∵ ,
∴ 为等边三角形,
∴ , .
在 中, ,
∴ ,
∴ ,
∴ .
∵ ,
∴ .
16.(1)证明:连接,如图所示:
是的直径,是的中点,
是的中位线,
,
,
,
点在圆上,
为的切线
(2)解:过点作,垂足为,如图所示:
则,
,,
,
,
,
,
,
,,,
,,
,
阴影部分面积.
17.(1)证明:
(2)解:
18.解:∵AB=40,点C是AB的中点,
∴BC= AB=20cm,
∵AB⊥BD,
∴∠CBD=90°,
在Rt△BCD中,BC=20cm,DC=25cm,
∴BD= = =15(cm),
过点C1作C1H⊥BD1于点H,
则∠C1HD=C1HD1=90°,
在Rt△BC1H中,BC1=20cm,C1H=10cm,
∴∠C1BH=30°,故BH=10 cm,
则∠ABC1=60°,
故点A经过的路径的长为: ≈42(m),
在Rt△D1C1H中,D1C1=25cm,C1H=10cm,
∴D1H= = (cm),
∴BD1=BH+HD1=10 +5 ≈17.32+22.915=40.235(cm),
∴点D滑动的距离为:BD1-BD=40.235-15=25.235≈25(cm),
答:点D滑动的距离为25m,点A经过的路径的长为42m
一、单选题
1.已知半径为5的⊙O是△ABC的外接圆.若∠ABC=25°,则劣弧 的长为( )
A. B. C. D.
2.如图,在圆中半径OC弦AB,且弦AB=CO=2,则图中阴影部分面积为( )
A. B. C. D.
3.如图,在 ABCD中AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则的长为( )
A.
B.
C.
D.2
4.如图,在中,,,将绕点逆时针旋转后,到,点经过的路径为弧,已知,则图中阴影部分的面积为( ).
A.π B.π C.π D.π
5.已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
A. π B. C. π D.2
6.如图,圆锥底面圆的半径为4,则这个圆锥的侧面展开图中的长为( )
A. B. C. D.
7.如图,正五边形ABCDE边长为6,以A为圆心,AB为半径画圆,图中阴影部分的面积为( ).
A. B. C. D.
8.如图,某小区要绿化一扇形空地,准备在小扇形内种花在其余区域内(阴影部分)种草,测得,,,则种草区域的面积为( )
A. B. C. D.
二、填空题
9.在半径为3的圆中,圆心角所对的弧长是 .
10.如图,半径为4的扇形AOB的圆心角为90°,点D为半径OA的中点,CD⊥OA交于点C ,连接AC、CO,以点O为圆心OD为半径画弧分别交OC、OB于点F、E,则图中阴影部分的面积为 .
11.如图,分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为2,则勒洛三角形的周长为 .
12.如图,菱形OABC的边长为2,且点A、B、C在⊙O上,则劣弧 的长度为 .
13.如图是圆弧形状的铁轨示意图,半径OA的长度为200米,圆心角∠AOB=90°,则这段铁轨的长度为 米.(铁轨的宽度忽略不计,结果保留π)
三、解答题
14.一段铁丝长为4.5πcm,把它弯成半径为9cm的一段圆弧,求铁丝两端的距离.
15.如图,⊙O半径为10cm,AB是⊙O的一条弦且∠AOB=60°,求图中阴影部分的面积.
16.如图,以为直径的经过的中点,于点.
(1)求证:是的切线;
(2)当,时,求图中阴影部分的面积结果保留根号和.
17.如图所示,已知AB是的直径,C,D是上的点,交AD于点,连结BC.
(1)求证:AE=ED.
(2)若AB=10,∠CBD=36°,求的长.
18.如图所示的益智玩具由一块主板AB和一个支撑架CD组成,其侧面示意图如图1所示,测得AB⊥BD,AB=40cm,CD=25cm,点C为AB的中点.现为了方便儿童操作,需调整玩具的摆放,将AB绕点B顺时针旋转,CD绕点C旋转,同时点D做水平滑动(如图2),当点C1到BD的距离为10cm时停止运动,求点A经过的路径的长和点D滑动的距离.(结果保留整数,参考数据: ≈1.732, ≈4.583,π≈3.142)
答案
1.C
2.C
3.C
4.C
5.A
6.C
7.C
8.B
9.
10.
11.2π
12. π
13.100π
14.解:设弯成的圆弧所对的圆心角为n° ,
则有4.5π= ,
解得n=90°,
即圆心角为直角.
由勾股定理,求得铁丝两端间的距离为 (cm).
15.解:如图,作 于点C.
由圆的基本性质可知 ,
∵ ,
∴ 为等边三角形,
∴ , .
在 中, ,
∴ ,
∴ ,
∴ .
∵ ,
∴ .
16.(1)证明:连接,如图所示:
是的直径,是的中点,
是的中位线,
,
,
,
点在圆上,
为的切线
(2)解:过点作,垂足为,如图所示:
则,
,,
,
,
,
,
,
,,,
,,
,
阴影部分面积.
17.(1)证明:
(2)解:
18.解:∵AB=40,点C是AB的中点,
∴BC= AB=20cm,
∵AB⊥BD,
∴∠CBD=90°,
在Rt△BCD中,BC=20cm,DC=25cm,
∴BD= = =15(cm),
过点C1作C1H⊥BD1于点H,
则∠C1HD=C1HD1=90°,
在Rt△BC1H中,BC1=20cm,C1H=10cm,
∴∠C1BH=30°,故BH=10 cm,
则∠ABC1=60°,
故点A经过的路径的长为: ≈42(m),
在Rt△D1C1H中,D1C1=25cm,C1H=10cm,
∴D1H= = (cm),
∴BD1=BH+HD1=10 +5 ≈17.32+22.915=40.235(cm),
∴点D滑动的距离为:BD1-BD=40.235-15=25.235≈25(cm),
答:点D滑动的距离为25m,点A经过的路径的长为42m
同课章节目录
