2024年中考数学专题复习:1.3勾股定理的应用--勾股定理与翻折问题(无答案)
文档属性
| 名称 | 2024年中考数学专题复习:1.3勾股定理的应用--勾股定理与翻折问题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 975.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 15:12:23 | ||
图片预览

文档简介
2023-2024中考专题复习——1.3勾股定理的应用--勾股定理与翻折问题
1如图,△ABC中,∠ACB=90°,AC=4,BC=3,将△ADE沿DE翻折,使点A与点B重合,则AE的长为( )
A. B.3 C. D.
2如图,在中,,,.将折叠,使点B恰好落在边AC上.与点重合,AE为折痕,则的长为( )
A.12 B.25 C.20 D.15
3如图,中,,M,N分别是边上的两个动点.将沿直线折叠,使得点A的对应点D落在边的三等分点处,则线段的长为( )
A.3 B. C.3或 D.3或
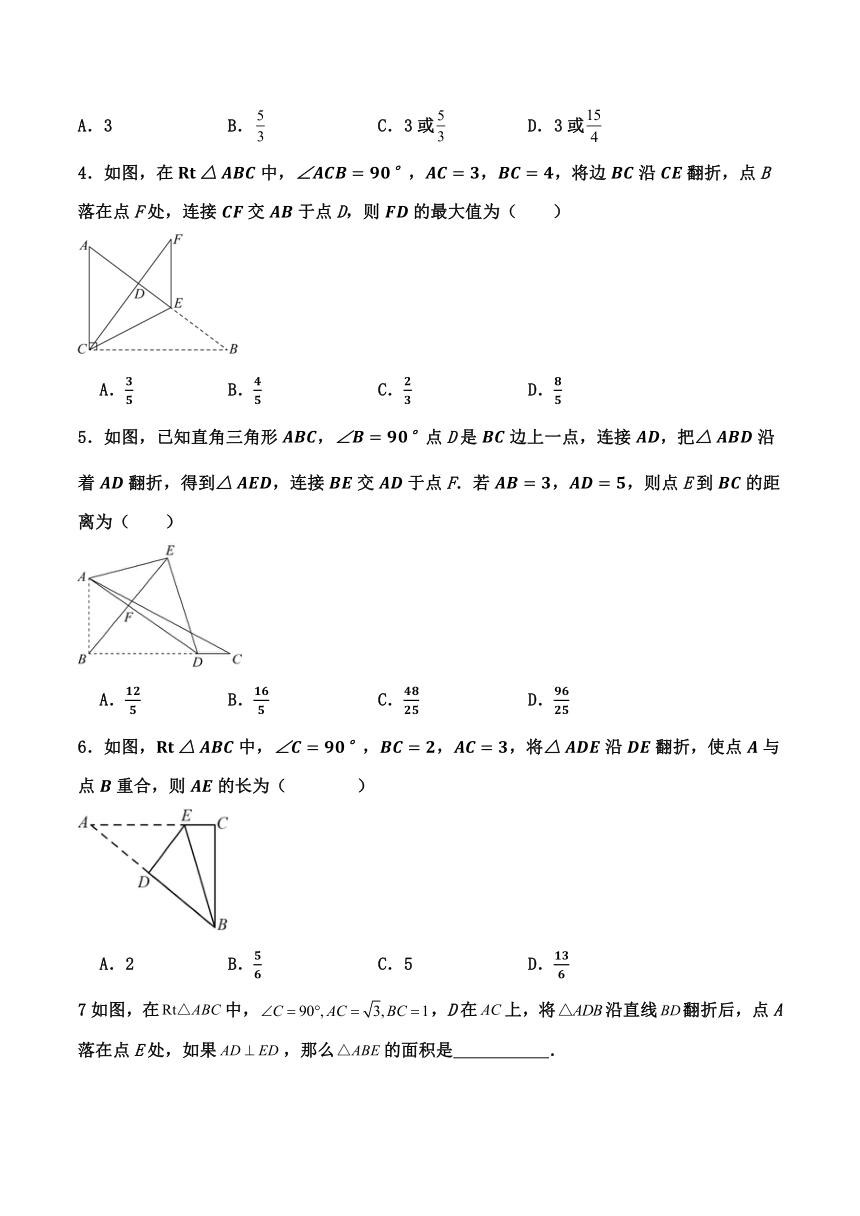
4.如图,在中,,,,将边沿翻折,点B落在点F处,连接交于点D,则的最大值为( )
A. B. C. D.
5.如图,已知直角三角形,点D是边上一点,连接,把沿着翻折,得到,连接交于点F.若,,则点E到的距离为( )
A. B. C. D.
6.如图,中,,,,将沿翻折,使点与点重合,则的长为( )
A.2 B. C.5 D.
7如图,在中,,D在上,将沿直线翻折后,点A落在点E处,如果,那么的面积是 .
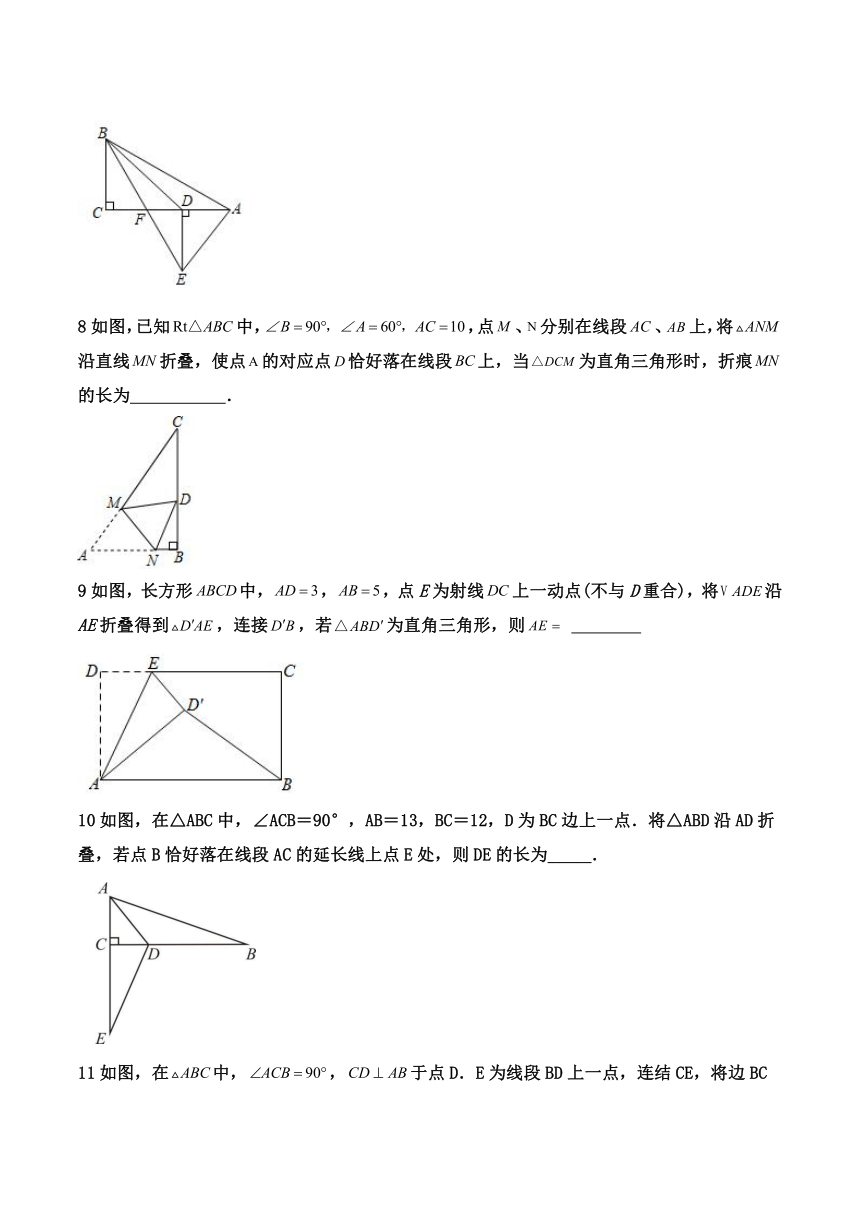
8如图,已知中,,点、分别在线段、上,将沿直线折叠,使点的对应点恰好落在线段上,当为直角三角形时,折痕的长为 .
9如图,长方形中,,,点E为射线上一动点(不与D重合),将沿AE折叠得到,连接,若为直角三角形,则
10如图,在△ABC中,∠ACB=90°,AB=13,BC=12,D为BC边上一点.将△ABD沿AD折叠,若点B恰好落在线段AC的延长线上点E处,则DE的长为_____.
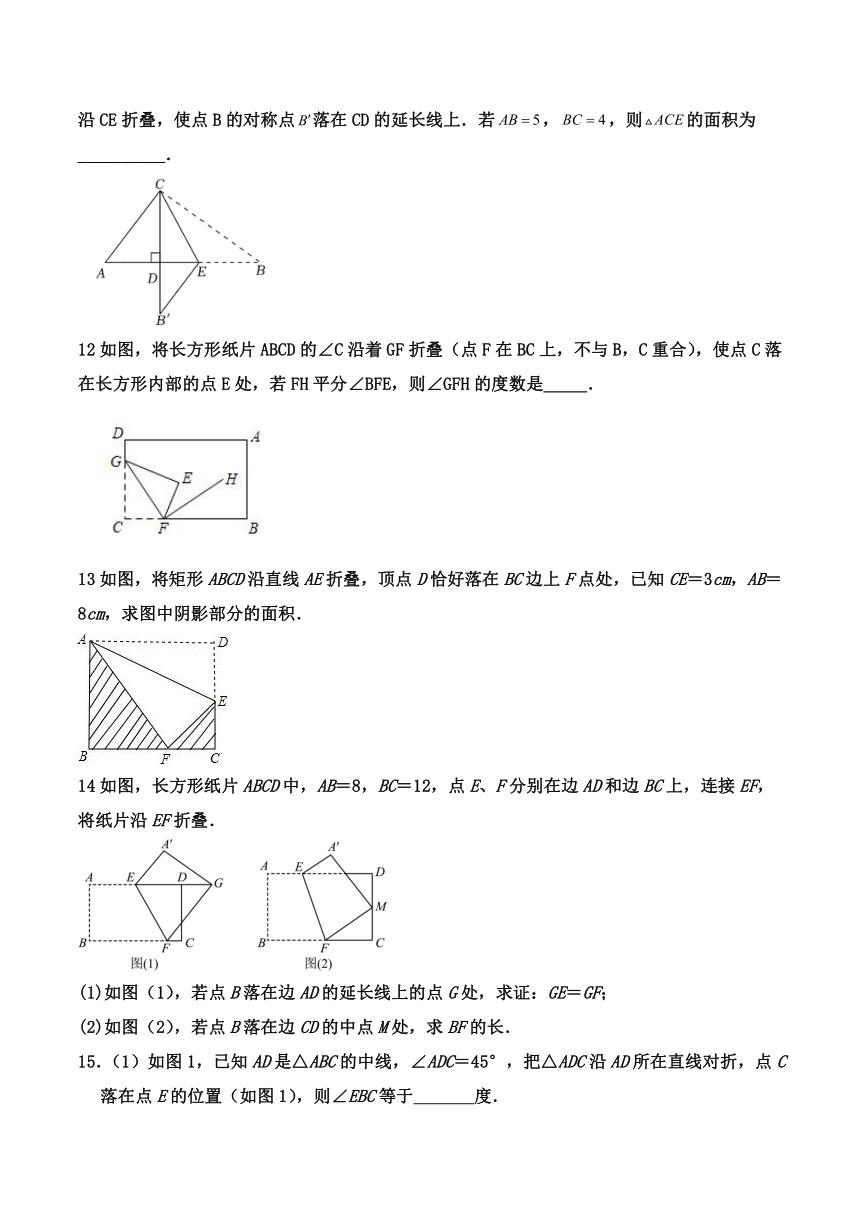
11如图,在中,,于点D.E为线段BD上一点,连结CE,将边BC沿CE折叠,使点B的对称点落在CD的延长线上.若,,则的面积为__________.
12如图,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部的点E处,若FH平分∠BFE,则∠GFH的度数是_____.
13如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=3cm,AB=8cm,求图中阴影部分的面积.
14如图,长方形纸片ABCD中,AB=8,BC=12,点E、F分别在边AD和边BC上,连接EF,将纸片沿EF折叠.
(1)如图(1),若点B落在边AD的延长线上的点G处,求证:GE=GF;
(2)如图(2),若点B落在边CD的中点M处,求BF的长.
15.(1)如图1,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿AD所在直线对折,点C落在点E的位置(如图1),则∠EBC等于 度.
(2)如图2,有一直角三角形纸片,两直角边AC=3,BC=4,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
16.如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B'处,点A落在点A'处.
(1)试说明B'E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的关系,并说明理由.
17如图,将边长为12cm的正方形折叠,使A点落在边上的E点,然后压平得折痕,若的长为13cm,求线段的长.
18如图,已知正方形的边长,E为边上一点且长为,动点P从点B出发以每秒的速度沿射线方向运动.在点P的运动过程中,把沿折叠,点B落在点处.设运动时间为t秒.
(1)当 时,为直角;
(2)是否存在某一时刻t,使得点到直线的距离为?若存在,请求出所有符合题意的t的值;若不存在,请说明理由.
19.如图1,为了探究某种类型矩形ABCD的性质,数学项目学习小组在BC边上取一点E,连接DE.经探究发现:当DE平分∠ADC时,将△ABE沿AE折叠至△AFE,点F恰好落在DE上.据此解决下列问题:
(1)求证:△AFD≌△DCE;
(2)如图2,延长CF交AE于点G,交AB于点H.
①求证:AH·AF=AG·CF ;
②求GH∶DF的值.
20.在矩形ABCD中,,P是边AB上一点,把沿直线PC折叠,顶点B的对应点是点G,过点B作,垂足为E且在AD上,BE交PC于点F.
(1)如图1,若点E是AD的中点,求证:;
(2)如图2,当,且时,求的值;
(3)如图3,当时,求BP的值.
1如图,△ABC中,∠ACB=90°,AC=4,BC=3,将△ADE沿DE翻折,使点A与点B重合,则AE的长为( )
A. B.3 C. D.
2如图,在中,,,.将折叠,使点B恰好落在边AC上.与点重合,AE为折痕,则的长为( )
A.12 B.25 C.20 D.15
3如图,中,,M,N分别是边上的两个动点.将沿直线折叠,使得点A的对应点D落在边的三等分点处,则线段的长为( )
A.3 B. C.3或 D.3或
4.如图,在中,,,,将边沿翻折,点B落在点F处,连接交于点D,则的最大值为( )
A. B. C. D.
5.如图,已知直角三角形,点D是边上一点,连接,把沿着翻折,得到,连接交于点F.若,,则点E到的距离为( )
A. B. C. D.
6.如图,中,,,,将沿翻折,使点与点重合,则的长为( )
A.2 B. C.5 D.
7如图,在中,,D在上,将沿直线翻折后,点A落在点E处,如果,那么的面积是 .
8如图,已知中,,点、分别在线段、上,将沿直线折叠,使点的对应点恰好落在线段上,当为直角三角形时,折痕的长为 .
9如图,长方形中,,,点E为射线上一动点(不与D重合),将沿AE折叠得到,连接,若为直角三角形,则
10如图,在△ABC中,∠ACB=90°,AB=13,BC=12,D为BC边上一点.将△ABD沿AD折叠,若点B恰好落在线段AC的延长线上点E处,则DE的长为_____.
11如图,在中,,于点D.E为线段BD上一点,连结CE,将边BC沿CE折叠,使点B的对称点落在CD的延长线上.若,,则的面积为__________.
12如图,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部的点E处,若FH平分∠BFE,则∠GFH的度数是_____.
13如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=3cm,AB=8cm,求图中阴影部分的面积.
14如图,长方形纸片ABCD中,AB=8,BC=12,点E、F分别在边AD和边BC上,连接EF,将纸片沿EF折叠.
(1)如图(1),若点B落在边AD的延长线上的点G处,求证:GE=GF;
(2)如图(2),若点B落在边CD的中点M处,求BF的长.
15.(1)如图1,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿AD所在直线对折,点C落在点E的位置(如图1),则∠EBC等于 度.
(2)如图2,有一直角三角形纸片,两直角边AC=3,BC=4,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
16.如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B'处,点A落在点A'处.
(1)试说明B'E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的关系,并说明理由.
17如图,将边长为12cm的正方形折叠,使A点落在边上的E点,然后压平得折痕,若的长为13cm,求线段的长.
18如图,已知正方形的边长,E为边上一点且长为,动点P从点B出发以每秒的速度沿射线方向运动.在点P的运动过程中,把沿折叠,点B落在点处.设运动时间为t秒.
(1)当 时,为直角;
(2)是否存在某一时刻t,使得点到直线的距离为?若存在,请求出所有符合题意的t的值;若不存在,请说明理由.
19.如图1,为了探究某种类型矩形ABCD的性质,数学项目学习小组在BC边上取一点E,连接DE.经探究发现:当DE平分∠ADC时,将△ABE沿AE折叠至△AFE,点F恰好落在DE上.据此解决下列问题:
(1)求证:△AFD≌△DCE;
(2)如图2,延长CF交AE于点G,交AB于点H.
①求证:AH·AF=AG·CF ;
②求GH∶DF的值.
20.在矩形ABCD中,,P是边AB上一点,把沿直线PC折叠,顶点B的对应点是点G,过点B作,垂足为E且在AD上,BE交PC于点F.
(1)如图1,若点E是AD的中点,求证:;
(2)如图2,当,且时,求的值;
(3)如图3,当时,求BP的值.
同课章节目录
