2023-—2024学年沪科版数学九年级下册第26章 概率初步 单元检测(含答案)
文档属性
| 名称 | 2023-—2024学年沪科版数学九年级下册第26章 概率初步 单元检测(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 242.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 15:11:21 | ||
图片预览




文档简介
第26章 概率初步
(时间:120分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.“某人投篮一次,投中篮筐”这一事件是 ( )
A.随机事件 B.必然事件 C.不可能事件 D.确定事件
2.下列事件中,属于随机事件的是 ( )
A.百步穿杨 B.水涨船高 C.水中捞月 D.冬去春来
3.天气预报称,明天芜湖市全市的降水率为90%,下列理解正确的是 ( )
A.明天芜湖市全市下雨的可能性较大
B.明天芜湖市全市有90%的地方会下雨
C.明天芜湖市全天有90%的时间会下雨
D.明天芜湖市一定会下雨
4.如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,事件“指针所指扇形中的数小于3”的概率为 ( )
A. B. C. D.2
5.甲、乙两名同学在一次用频率估计概率的试验中,统计了某一结果出现的频率,并绘制出如下折线统计图,则最有可能符合这一结果的试验是 ( )
A.掷一枚正六面体的骰子,出现点数为1的概率
B.抛一枚硬币,出现正面的概率
C.任意写一个整数,它能被3整除的概率
D.从一副去掉大小王的扑克牌中,任意抽取一张,抽到黑桃的概率
6.如图,随机闭合开关S1,S2,S3中的两个,灯泡不会发光的概率是 ( )
A. B. C. D.
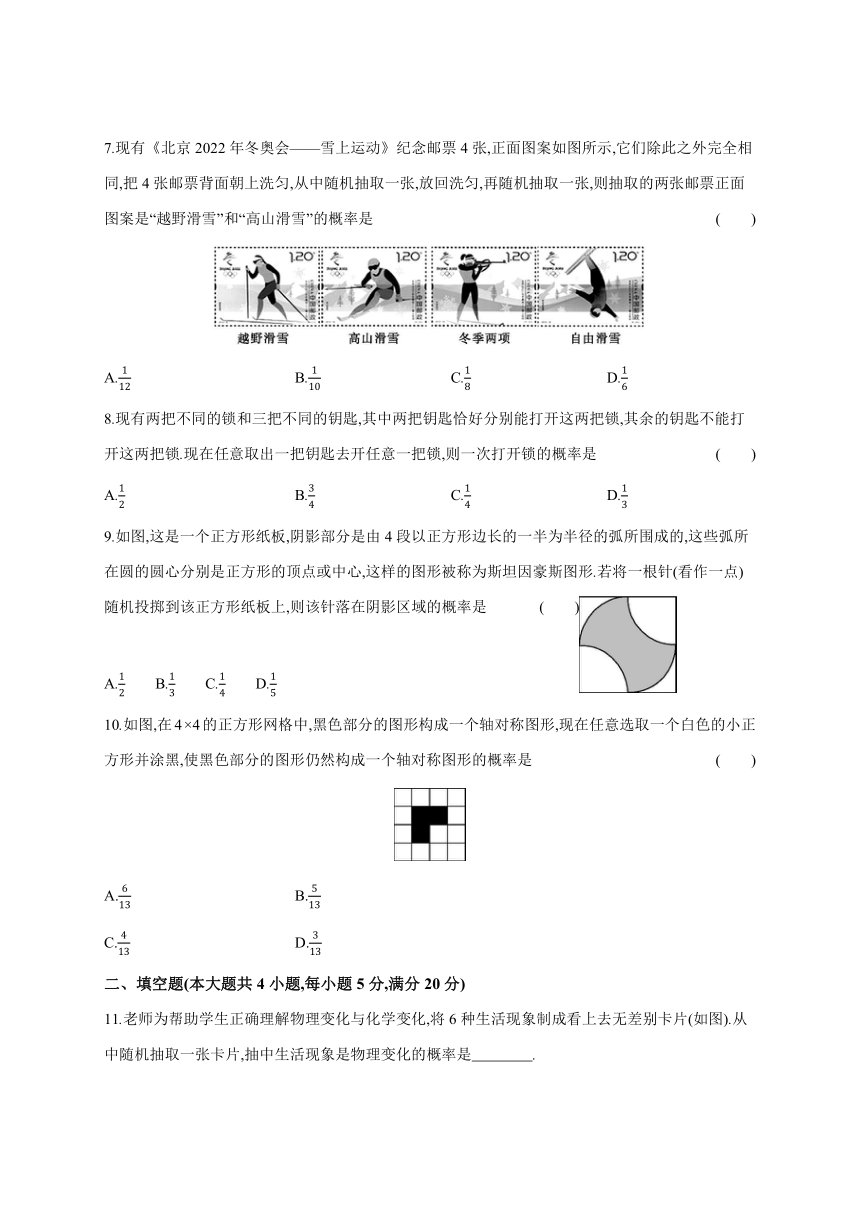
7.现有《北京2022年冬奥会——雪上运动》纪念邮票4张,正面图案如图所示,它们除此之外完全相同,把4张邮票背面朝上洗匀,从中随机抽取一张,放回洗匀,再随机抽取一张,则抽取的两张邮票正面图案是“越野滑雪”和“高山滑雪”的概率是 ( )
A. B. C. D.
8.现有两把不同的锁和三把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁.现在任意取出一把钥匙去开任意一把锁,则一次打开锁的概率是 ( )
A. B. C. D.
9.如图,这是一个正方形纸板,阴影部分是由4段以正方形边长的一半为半径的弧所围成的,这些弧所在圆的圆心分别是正方形的顶点或中心,这样的图形被称为斯坦因豪斯图形.若将一根针(看作一点)随机投掷到该正方形纸板上,则该针落在阴影区域的概率是 ( )
A. B. C. D.
10.如图,在4×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是 ( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.老师为帮助学生正确理解物理变化与化学变化,将6种生活现象制成看上去无差别卡片(如图).从中随机抽取一张卡片,抽中生活现象是物理变化的概率是 .
12.某校八年级的学生有1000人购买校服,校服按大小分为小号、中号、大号、特大号4种,在调查得到的数据中,小号、中号、大号出现的频数分别是250、420、280,则特大号出现的频率是 .
13.在m2□6m□9的“□”中任意填上“+”或“-”号,则所得代数式为完全平方式的概率为 .
14.某疫苗接种点有4个完全相同的冷藏箱用来储存疫苗,同一冷藏箱里的疫苗都来自同一厂家,其中有两个冷藏箱储存A厂家的疫苗,另外两个冷藏箱分别储存B厂家和C厂家的疫苗.
(1)如果从中随机拿出两个冷藏箱,送往1号和2号接种台,那么拿出的两个冷藏箱里有A厂家疫苗的概率是 .
(2)如果将4个冷藏箱随机送往4个接种台,每个接种台接受一个冷藏箱,那么1号接种台恰好接受A厂家疫苗的概率是 .
三、(本大题共2小题,每小题8分,满分16分)
15.不透明的箱子里有4个红球和a个白球,这些球除颜色外均无差别,小李从中摸出一个球,摸到的球是白球的概率是,求a的值.
16.2022年3月23日“天宫课堂”第二课在中国空间站正式开讲了,“太空教师”翟志刚、王亚平、叶光富又上了一堂精彩的太空科普课.某学校为了培养学生对航天知识的学习兴趣,将举办航天知识讲座.现决定从A、B、C、D四名志愿者中随机选取两名志愿者担任引导员.
(1)“B志愿者被选中”是 事件.(填“随机”或“不可能”或“必然”)
(2)请用列表或画树状图的方法求出抽到A,B两名志愿者的概率.
四、(本大题共2小题,每小题8分,满分16分)
17.某种油菜籽在相同条件下的发芽试验的结果如下:
每批粒数n 100 150 200 500 800 1000
发芽的粒数m 65 111 136 345 560 700
发芽的频率 0.65 0.74 0.68 0.69 a b
(1)上表中a= ,b= .
(2)请估计,当n很大时,频率将会接近 .
(3)这种油菜籽发芽的概率的估计值是多少 请简要说明理由.
(4)如果该种油菜籽发芽后的成秧率为90%,则在相同条件下用10000粒该种油菜籽估计可得到油菜秧苗多少棵
18.小明和小刚用如图所示的两个转盘做游戏,游戏规则如下:分别旋转两个转盘,若所转到的数字之积为奇数,则小明得2分;若所转到的数字之积为偶数,则小明得1分.这个游戏对双方公平吗 若公平,请说明理由;若不公平,如何修改规则才能使游戏双方公平
五、(本大题共2小题,每小题10分,满分20分)
19.数学课上,师生进行了摸球试验:一只不透明的袋子中装有编号分别为1、2、3、…、m的小球(除编号外完全相同):
活动一:当m=2时,从中随机摸出一个球记录编号后放回袋中并摇匀,再随机摸出一个球记录下编号后放回袋中并摇匀,重复上述操作,若事件:“记录的编号中出现两个相同的编号”是必然事件,则最少需摸 次.
活动二:当m=3时,从中随机摸出一个球记录编号后放回袋中并摇匀,再随机摸出一个球记录下编号后放回袋中并摇匀,重复上述操作.
(1)若事件A:“记录的编号中出现两个相同的编号”是必然事件,则最少需摸 次.
(2)若事件B:“记录的编号中出现三个相同的编号”是必然事件,则最少需摸 次.
活动三:在这只装有编号分别为1、2、3、…、m的小球(除编号外完全相同)的不透明的袋子中,从中随机摸出一个球记录编号后放回袋中并摇匀,再随机摸出一个球记录下编号后放回袋中并摇匀,重复上述操作,若事件:“记录的编号中出现4个相同的编号”是必然事件至少需要摸100次,则袋中有多少个小球
20.三相电缆线是由火线,零线和接地线三股组成.如图,有甲、乙两根三相电缆线,A与A1代表火线,B与B1代表零线,C与C1代表接地线,现将这两根三相电缆线连接成一根.
(1)若从乙的三股中随机选一股与甲中的火线对接,恰好接对(A与A1)的概率是多少
(2)若两根电缆线的接头都是一对一随机对接的,恰好全部接对的概率是多少
六、(本题满分12分)
21.某中学全校师生听取了“禁毒”宣传报告后,对禁毒人员肃然起敬.学校德育处随后决定在全校1000名学生中开展“我为禁毒献爱心”的捐款活动.张老师在周五随机调查了20名学生随身携带零花钱的情况,并将收集的数据进行整理,绘制出如图所示的条形统计图.
(1)求这组数据的平均数和众数.
(2)经调查,当学生身上的零花钱多于15元时,都自愿捐出零花钱的20%,其余学生不参加捐款.请你估计周五这一天该校可能收到学生自愿捐款多少元
(3)捐款最多的两人将和另一个学校选出的两人组成一个“禁毒”知识宣讲小组,若从这4人中随机指定两人担任正、副组长,求这两人来自不同学校的概率.
七、(本题满分12分)
22.在正方形ABCD的顶点上有顺时针移动的点P,最初停在顶点A上,每掷1个骰子,前进掷出的数.例如,掷出数字3时,停在点D,掷出数字5时,停在点B.另外,掷2次骰子时,第2次从第1次停止点开始移动.
(1)掷1次骰子后,求点P位于点B的概率.
(2)掷2 次骰子后,求点P位于点C的概率.
八、(本题满分14分)
23.五一假期,某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图所示是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题.
(1)若去丁地的车票占全部车票的10%,请求出去丁地的车票数量,并补全如下统计图.
(2)若公司采用随机抽取的方式发车票,员工小胡先从所有的车票中随机抽取一张(所有车票的形状、大小、质地完全相同、均匀),则小胡抽到去甲地的车票的概率是多少
(3)若有一张商务座,小王和小李都想拿到,决定采取摸球的方式确定,具体规则:每人从不透明的袋子中摸出分别标有1、2、3、4的四个球中的一个球(球除数字不同外完全相同),并放回让另一个人摸,若小王摸得的数字比小李的小,车票给小王,否则给小李.试用列表法或画树状图的方法分析这个规则对双方是否公平.
参考答案
1.A 2.A 3.A 4.B 5.C 6.B 7.C 8.D 9.A 10.B
11. 12.0.05 13.
14.(1)(2分)
(2)(3分)
15.解:∵摸出一个球,摸到的球是白球的概率是,
∴=,
解得a=6. 6分
经检验,a=6是原方程的根,
∴a的值为6. 8分
16.解:(1)随机. 2分
(2)根据题意画树状图如下:
共有12种等可能的情况数,其中抽到A,B两名志愿者有2种,
则抽到A,B两名志愿者的概率是=. 8分
17.解:(1)0.70; 0.70. 2分
(2)0.70. 4分
(3)这种油菜籽发芽的概率估计值是0.70.理由:在相同条件下,当实验次数很大时,事件发生的频率可作为概率的近似值. 6分
(4)10000×0.70×90%=6300(棵).
答:10000粒该种油菜籽可得到油菜秧苗6300棵. 8分
18.解:积是奇数的概率==,积是偶数的概率==, 3分
∴小明的得分为×2==,小刚的得分为×1==, 6分
∴这个游戏对双方是公平的. 8分
19.解:活动一:3. 2分
活动二:(1)4. 4分
(2)7. 6分
活动三:根据题意得m+m+m+1=100,
解得m=33.
答:袋中有33个小球. 10分
20.解:(1)若从乙的三股中随机选一股与甲中的火线对接,恰好接对(A与A1)的概率是=. 3分
(2)画树状图为
共有6种等可能的结果数,其中恰好全部接对的结果数为1,
所以恰好全部接对的概率是. 10分
21.解:(1)这组数据的平均数==20.5,
其中20元出现的次数最多, 2分
∴这组数据的众数为20. 4分
(2)随机调查的20人中,身上的零花钱多于15元的有12人,
估计周五这一天该校可能收到学生自愿捐款为1000××20×20%+1000××25×20%+1000××30×20%+1000××40×20%=3150(元). 7分
(3)把捐款最多的两人记为A、B,另一个学校选出的两人记为C、D,
画树状图如下:
10分
由树状图可知,共有12种等可能的结果,两人来自不同学校的结果有8种,
∴两人来自不同学校的概率为=. 12分
22.解:(1)掷1次骰子,掷出的数字与点P移动后的位置对应如下,共有6种等可能的结果,其中点P位于点B的结果有2种,故掷1次骰子后,点P位于点B的概率为,即. 4分
掷出的数 点P移动后的位置
1 B
2 C
3 D
4 A
5=4+1 B
6=4+2 C
(2)由(1)可知掷出的数1,2,3,4分别对应的点P的位置为B,C,D,A,掷出的数大于4时,点P移动的位置发生循环运动,循环节为4,由题意列表如下,共有36种等可能的结果,除去循环的部分,尾数是2的结果共有9种,故掷2次骰子后,点P位于点C的概率为,即. 12分
a+b 1 2 3 4 5 6
1 1+1=2 1+2=3 1+3=4 1+4=4+1 1+5=4+2 1+6=4+3
2 2+1=3 2+2=4 2+3=4+1 2+4=4+2 2+5=4+3 2+6=4+4
3 3+1=4 3+2=4+1 3+3=4+2 3+4=4+3 3+5=4+4 3+6=8+1
4 4+1=4+1 4+2=4+2 4+3=4+3 4+4=4+4 4+5=8+1 4+6=8+2
5 5+1=4+2 5+2=4+3 5+3=4+4 5+4=8+1 5+5=8+2 5+6=8+3
6 6+1=4+3 6+2=4+4 6+3=8+1 6+4=8+2 6+5=8+3 6+6=8+4
23.解:(1)根据题意得(20+40+30)÷(1-10%)=100(张),
则去丁地的车票数为100-(20+40+30)=10(张). 2分
补图如下.
5分
(2)总票数为100张,去甲地的票数为20张,
则员工小胡抽到去甲地的车票的概率为=. 8分
(3)列表如下(画树状图略):
小王 小李 1 2 3 4
1 (1,1) (2,1) (3,1) (4,1)
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
由上表可知所有等可能的情况有16种, 10分
其中小王摸到的数字比小李摸到的数字小的情况有6种,分别为(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),
∴P(小王得车票)==, 12分
则P(小李得车票)=1-=,
则这个规则不公平. 14分
(时间:120分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.“某人投篮一次,投中篮筐”这一事件是 ( )
A.随机事件 B.必然事件 C.不可能事件 D.确定事件
2.下列事件中,属于随机事件的是 ( )
A.百步穿杨 B.水涨船高 C.水中捞月 D.冬去春来
3.天气预报称,明天芜湖市全市的降水率为90%,下列理解正确的是 ( )
A.明天芜湖市全市下雨的可能性较大
B.明天芜湖市全市有90%的地方会下雨
C.明天芜湖市全天有90%的时间会下雨
D.明天芜湖市一定会下雨
4.如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,事件“指针所指扇形中的数小于3”的概率为 ( )
A. B. C. D.2
5.甲、乙两名同学在一次用频率估计概率的试验中,统计了某一结果出现的频率,并绘制出如下折线统计图,则最有可能符合这一结果的试验是 ( )
A.掷一枚正六面体的骰子,出现点数为1的概率
B.抛一枚硬币,出现正面的概率
C.任意写一个整数,它能被3整除的概率
D.从一副去掉大小王的扑克牌中,任意抽取一张,抽到黑桃的概率
6.如图,随机闭合开关S1,S2,S3中的两个,灯泡不会发光的概率是 ( )
A. B. C. D.
7.现有《北京2022年冬奥会——雪上运动》纪念邮票4张,正面图案如图所示,它们除此之外完全相同,把4张邮票背面朝上洗匀,从中随机抽取一张,放回洗匀,再随机抽取一张,则抽取的两张邮票正面图案是“越野滑雪”和“高山滑雪”的概率是 ( )
A. B. C. D.
8.现有两把不同的锁和三把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁.现在任意取出一把钥匙去开任意一把锁,则一次打开锁的概率是 ( )
A. B. C. D.
9.如图,这是一个正方形纸板,阴影部分是由4段以正方形边长的一半为半径的弧所围成的,这些弧所在圆的圆心分别是正方形的顶点或中心,这样的图形被称为斯坦因豪斯图形.若将一根针(看作一点)随机投掷到该正方形纸板上,则该针落在阴影区域的概率是 ( )
A. B. C. D.
10.如图,在4×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是 ( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.老师为帮助学生正确理解物理变化与化学变化,将6种生活现象制成看上去无差别卡片(如图).从中随机抽取一张卡片,抽中生活现象是物理变化的概率是 .
12.某校八年级的学生有1000人购买校服,校服按大小分为小号、中号、大号、特大号4种,在调查得到的数据中,小号、中号、大号出现的频数分别是250、420、280,则特大号出现的频率是 .
13.在m2□6m□9的“□”中任意填上“+”或“-”号,则所得代数式为完全平方式的概率为 .
14.某疫苗接种点有4个完全相同的冷藏箱用来储存疫苗,同一冷藏箱里的疫苗都来自同一厂家,其中有两个冷藏箱储存A厂家的疫苗,另外两个冷藏箱分别储存B厂家和C厂家的疫苗.
(1)如果从中随机拿出两个冷藏箱,送往1号和2号接种台,那么拿出的两个冷藏箱里有A厂家疫苗的概率是 .
(2)如果将4个冷藏箱随机送往4个接种台,每个接种台接受一个冷藏箱,那么1号接种台恰好接受A厂家疫苗的概率是 .
三、(本大题共2小题,每小题8分,满分16分)
15.不透明的箱子里有4个红球和a个白球,这些球除颜色外均无差别,小李从中摸出一个球,摸到的球是白球的概率是,求a的值.
16.2022年3月23日“天宫课堂”第二课在中国空间站正式开讲了,“太空教师”翟志刚、王亚平、叶光富又上了一堂精彩的太空科普课.某学校为了培养学生对航天知识的学习兴趣,将举办航天知识讲座.现决定从A、B、C、D四名志愿者中随机选取两名志愿者担任引导员.
(1)“B志愿者被选中”是 事件.(填“随机”或“不可能”或“必然”)
(2)请用列表或画树状图的方法求出抽到A,B两名志愿者的概率.
四、(本大题共2小题,每小题8分,满分16分)
17.某种油菜籽在相同条件下的发芽试验的结果如下:
每批粒数n 100 150 200 500 800 1000
发芽的粒数m 65 111 136 345 560 700
发芽的频率 0.65 0.74 0.68 0.69 a b
(1)上表中a= ,b= .
(2)请估计,当n很大时,频率将会接近 .
(3)这种油菜籽发芽的概率的估计值是多少 请简要说明理由.
(4)如果该种油菜籽发芽后的成秧率为90%,则在相同条件下用10000粒该种油菜籽估计可得到油菜秧苗多少棵
18.小明和小刚用如图所示的两个转盘做游戏,游戏规则如下:分别旋转两个转盘,若所转到的数字之积为奇数,则小明得2分;若所转到的数字之积为偶数,则小明得1分.这个游戏对双方公平吗 若公平,请说明理由;若不公平,如何修改规则才能使游戏双方公平
五、(本大题共2小题,每小题10分,满分20分)
19.数学课上,师生进行了摸球试验:一只不透明的袋子中装有编号分别为1、2、3、…、m的小球(除编号外完全相同):
活动一:当m=2时,从中随机摸出一个球记录编号后放回袋中并摇匀,再随机摸出一个球记录下编号后放回袋中并摇匀,重复上述操作,若事件:“记录的编号中出现两个相同的编号”是必然事件,则最少需摸 次.
活动二:当m=3时,从中随机摸出一个球记录编号后放回袋中并摇匀,再随机摸出一个球记录下编号后放回袋中并摇匀,重复上述操作.
(1)若事件A:“记录的编号中出现两个相同的编号”是必然事件,则最少需摸 次.
(2)若事件B:“记录的编号中出现三个相同的编号”是必然事件,则最少需摸 次.
活动三:在这只装有编号分别为1、2、3、…、m的小球(除编号外完全相同)的不透明的袋子中,从中随机摸出一个球记录编号后放回袋中并摇匀,再随机摸出一个球记录下编号后放回袋中并摇匀,重复上述操作,若事件:“记录的编号中出现4个相同的编号”是必然事件至少需要摸100次,则袋中有多少个小球
20.三相电缆线是由火线,零线和接地线三股组成.如图,有甲、乙两根三相电缆线,A与A1代表火线,B与B1代表零线,C与C1代表接地线,现将这两根三相电缆线连接成一根.
(1)若从乙的三股中随机选一股与甲中的火线对接,恰好接对(A与A1)的概率是多少
(2)若两根电缆线的接头都是一对一随机对接的,恰好全部接对的概率是多少
六、(本题满分12分)
21.某中学全校师生听取了“禁毒”宣传报告后,对禁毒人员肃然起敬.学校德育处随后决定在全校1000名学生中开展“我为禁毒献爱心”的捐款活动.张老师在周五随机调查了20名学生随身携带零花钱的情况,并将收集的数据进行整理,绘制出如图所示的条形统计图.
(1)求这组数据的平均数和众数.
(2)经调查,当学生身上的零花钱多于15元时,都自愿捐出零花钱的20%,其余学生不参加捐款.请你估计周五这一天该校可能收到学生自愿捐款多少元
(3)捐款最多的两人将和另一个学校选出的两人组成一个“禁毒”知识宣讲小组,若从这4人中随机指定两人担任正、副组长,求这两人来自不同学校的概率.
七、(本题满分12分)
22.在正方形ABCD的顶点上有顺时针移动的点P,最初停在顶点A上,每掷1个骰子,前进掷出的数.例如,掷出数字3时,停在点D,掷出数字5时,停在点B.另外,掷2次骰子时,第2次从第1次停止点开始移动.
(1)掷1次骰子后,求点P位于点B的概率.
(2)掷2 次骰子后,求点P位于点C的概率.
八、(本题满分14分)
23.五一假期,某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图所示是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题.
(1)若去丁地的车票占全部车票的10%,请求出去丁地的车票数量,并补全如下统计图.
(2)若公司采用随机抽取的方式发车票,员工小胡先从所有的车票中随机抽取一张(所有车票的形状、大小、质地完全相同、均匀),则小胡抽到去甲地的车票的概率是多少
(3)若有一张商务座,小王和小李都想拿到,决定采取摸球的方式确定,具体规则:每人从不透明的袋子中摸出分别标有1、2、3、4的四个球中的一个球(球除数字不同外完全相同),并放回让另一个人摸,若小王摸得的数字比小李的小,车票给小王,否则给小李.试用列表法或画树状图的方法分析这个规则对双方是否公平.
参考答案
1.A 2.A 3.A 4.B 5.C 6.B 7.C 8.D 9.A 10.B
11. 12.0.05 13.
14.(1)(2分)
(2)(3分)
15.解:∵摸出一个球,摸到的球是白球的概率是,
∴=,
解得a=6. 6分
经检验,a=6是原方程的根,
∴a的值为6. 8分
16.解:(1)随机. 2分
(2)根据题意画树状图如下:
共有12种等可能的情况数,其中抽到A,B两名志愿者有2种,
则抽到A,B两名志愿者的概率是=. 8分
17.解:(1)0.70; 0.70. 2分
(2)0.70. 4分
(3)这种油菜籽发芽的概率估计值是0.70.理由:在相同条件下,当实验次数很大时,事件发生的频率可作为概率的近似值. 6分
(4)10000×0.70×90%=6300(棵).
答:10000粒该种油菜籽可得到油菜秧苗6300棵. 8分
18.解:积是奇数的概率==,积是偶数的概率==, 3分
∴小明的得分为×2==,小刚的得分为×1==, 6分
∴这个游戏对双方是公平的. 8分
19.解:活动一:3. 2分
活动二:(1)4. 4分
(2)7. 6分
活动三:根据题意得m+m+m+1=100,
解得m=33.
答:袋中有33个小球. 10分
20.解:(1)若从乙的三股中随机选一股与甲中的火线对接,恰好接对(A与A1)的概率是=. 3分
(2)画树状图为
共有6种等可能的结果数,其中恰好全部接对的结果数为1,
所以恰好全部接对的概率是. 10分
21.解:(1)这组数据的平均数==20.5,
其中20元出现的次数最多, 2分
∴这组数据的众数为20. 4分
(2)随机调查的20人中,身上的零花钱多于15元的有12人,
估计周五这一天该校可能收到学生自愿捐款为1000××20×20%+1000××25×20%+1000××30×20%+1000××40×20%=3150(元). 7分
(3)把捐款最多的两人记为A、B,另一个学校选出的两人记为C、D,
画树状图如下:
10分
由树状图可知,共有12种等可能的结果,两人来自不同学校的结果有8种,
∴两人来自不同学校的概率为=. 12分
22.解:(1)掷1次骰子,掷出的数字与点P移动后的位置对应如下,共有6种等可能的结果,其中点P位于点B的结果有2种,故掷1次骰子后,点P位于点B的概率为,即. 4分
掷出的数 点P移动后的位置
1 B
2 C
3 D
4 A
5=4+1 B
6=4+2 C
(2)由(1)可知掷出的数1,2,3,4分别对应的点P的位置为B,C,D,A,掷出的数大于4时,点P移动的位置发生循环运动,循环节为4,由题意列表如下,共有36种等可能的结果,除去循环的部分,尾数是2的结果共有9种,故掷2次骰子后,点P位于点C的概率为,即. 12分
a+b 1 2 3 4 5 6
1 1+1=2 1+2=3 1+3=4 1+4=4+1 1+5=4+2 1+6=4+3
2 2+1=3 2+2=4 2+3=4+1 2+4=4+2 2+5=4+3 2+6=4+4
3 3+1=4 3+2=4+1 3+3=4+2 3+4=4+3 3+5=4+4 3+6=8+1
4 4+1=4+1 4+2=4+2 4+3=4+3 4+4=4+4 4+5=8+1 4+6=8+2
5 5+1=4+2 5+2=4+3 5+3=4+4 5+4=8+1 5+5=8+2 5+6=8+3
6 6+1=4+3 6+2=4+4 6+3=8+1 6+4=8+2 6+5=8+3 6+6=8+4
23.解:(1)根据题意得(20+40+30)÷(1-10%)=100(张),
则去丁地的车票数为100-(20+40+30)=10(张). 2分
补图如下.
5分
(2)总票数为100张,去甲地的票数为20张,
则员工小胡抽到去甲地的车票的概率为=. 8分
(3)列表如下(画树状图略):
小王 小李 1 2 3 4
1 (1,1) (2,1) (3,1) (4,1)
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
由上表可知所有等可能的情况有16种, 10分
其中小王摸到的数字比小李摸到的数字小的情况有6种,分别为(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),
∴P(小王得车票)==, 12分
则P(小李得车票)=1-=,
则这个规则不公平. 14分
