2023-—2024学年沪科版数学九年级上册第23章解直角三角形单元检测(含答案)
文档属性
| 名称 | 2023-—2024学年沪科版数学九年级上册第23章解直角三角形单元检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 308.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 15:10:28 | ||
图片预览



文档简介
第23章 解直角三角形
(时间:120分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.2tan 45°的值等于 ( )
A.2 B. C. D.1
2.如图,在Rt△ABC中,∠C=90°,AC=2,BC=3,则tan A的值为 ( )
A. B. C. D.
3.若cos A-=0,且∠A是锐角,则∠A的度数是 ( )
A.30° B.45°
C.60° D.90°
4.如图,在平面直角坐标系中,第一象限内射线OA与x轴正半轴的夹角为α,点P在射线OA上.若cos α=,则点P的坐标可能是 ( )
A.(3,5) B.(5,3)
C.(3,4) D.(4,3)
5.如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin ∠AOB的值等于 ( )
A. B.
C. D.
6.如图,某飞机在空中A处探测到它的正下方地平面上的目标C,此时飞机的飞行高度AC=1200 m,从飞机上看地平面指挥台B的俯角α=30°,则飞机A与指挥台B的距离为 ( )
A.1200 m B.1200 m
C.1200 m D.2400 m
7.如图,在△ABC中,AB=10,cos∠ABC=,D为边BC上一点,且AD=AC,若DC=4,则BD的值为 ( )
A.2 B.3
C.4 D.5
8.如图,在某次火箭发射过程中,火箭从地面到达A处时,在P处测得点A的仰角∠DPA为30°,且A与P两点的直线距离为10千米;当它沿铅垂线上升到达B处时,此时在P处测得点B的仰角∠DPB为45°,则从A处到B处的距离为(参考数据:≈1.7,≈1.4) ( )
A.1.5千米 B.2.0千米
C.2.5千米 D.3.5千米
9.图1是某公园的一个滑梯,图2是其示意图.滑梯的高BC为2 m,坡角∠A为60°,由于滑梯坡角过大存在安全隐患,公园管理局决定对滑梯进行整改,要在高度不变的前提下,通过加长滑梯的水平距离AB,使得坡角∠A满足30°≤∠A≤45°,则AB加长的距离可以是(参考数据:≈1.414,≈1.732) ( )
A.0.8 m B.1.6 m
C.2.4 m D.3.2 m
10.如图,在Rt△ABC中,∠BAC=90°,cos B=,D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使∠ADE=∠B,连接CE,则的值为 ( )
A. B.
C. D.3
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,已知CD=2,AC=3,则cos A= .
12.已知∠A,∠B,∠C是△ABC的三个内角,若|sin A-|+(cos B-)2=0,且∠A,∠B均为锐角,则∠C的度数为 .
13.如图,这是由边长相同的小正方形组成的网格,A、B、P、Q四点均在正方形网格的格点上,线段AB、PQ相交于点E,则tan∠AEP= .
14.如图,在Rt△ABC中,∠ABC=90°,AB=6,D是斜边AC上的一点,将△BCD沿BD翻折,使点C落到点C'处.
(1)若C'恰好是AB边的中点,则AC的长为 .
(2)若∠CBD=30°,连接AC',△ABC'正好是直角三角形,则BC的长为 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(π-)0-tan 60°·cos 30°.
16.如图,在Rt△ABC中,∠C=90°,AC=2,AB=3.求sin A的值.
四、(本大题共2小题,每小题8分,满分16分)
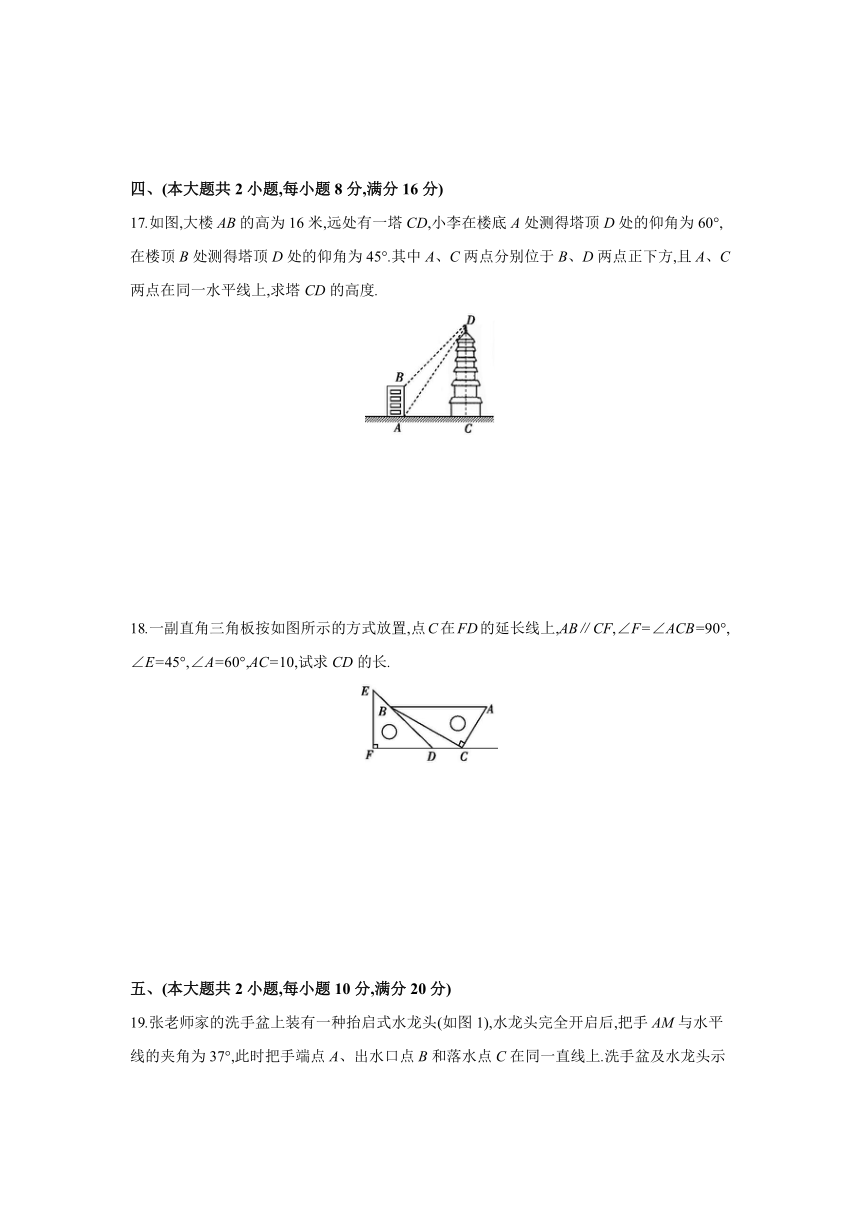
17.如图,大楼AB的高为16米,远处有一塔CD,小李在楼底A处测得塔顶D处的仰角为60°,在楼顶B处测得塔顶D处的仰角为45°.其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,求塔CD的高度.
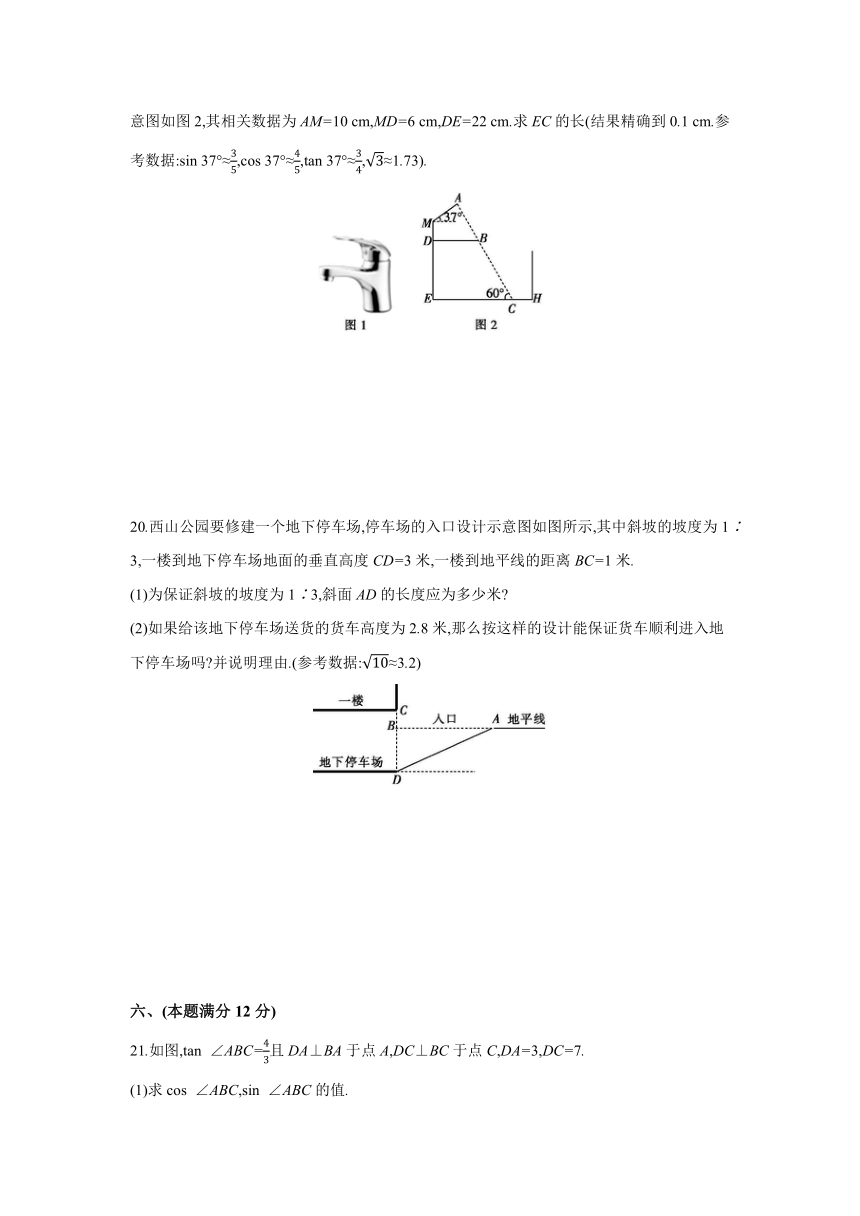
18.一副直角三角板按如图所示的方式放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
五、(本大题共2小题,每小题10分,满分20分)
19.张老师家的洗手盆上装有一种抬启式水龙头(如图1),水龙头完全开启后,把手AM与水平线的夹角为37°,此时把手端点A、出水口点B和落水点C在同一直线上.洗手盆及水龙头示意图如图2,其相关数据为AM=10 cm,MD=6 cm,DE=22 cm.求EC的长(结果精确到0.1 cm.参考数据:sin 37°≈,cos 37°≈,tan 37°≈,≈1.73).
20.西山公园要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的坡度为1∶3,一楼到地下停车场地面的垂直高度CD=3米,一楼到地平线的距离BC=1米.
(1)为保证斜坡的坡度为1∶3,斜面AD的长度应为多少米
(2)如果给该地下停车场送货的货车高度为2.8米,那么按这样的设计能保证货车顺利进入地下停车场吗 并说明理由.(参考数据:≈3.2)
六、(本题满分12分)
21.如图,tan ∠ABC=且DA⊥BA于点A,DC⊥BC于点C,DA=3,DC=7.
(1)求cos ∠ABC,sin ∠ABC的值.
(2)连接BD,求BD的长.
七、(本题满分12分)
22.数学老师布置了这样一个作业:
如果α,β都为锐角,且tan α=,tan β=,求α+β的度数.
甲、乙两位同学想利用正方形网格构图来解决问题,他们分别设计了图1和图2.
(1)请你分别利用图1、图2求出α+β的度数,并说明理由.
(2)请参考以上思考问题的方法,选择一种方法解决下面的问题.
如果α、β都为锐角,当tan α=5,tan β=时,在图3的正方形网格中,利用已作出的锐角α,画出∠MON,使得∠MON=α-β,直接写出α-β的度数,不必说明理由.
八、(本题满分14分)
23.在平面直角坐标系中,抛物线y=-x2+bx+c与y轴交于点A(0,3),与x轴的正半轴交于点B(5,0),点D在线段OB上,且OD=1,连接AD,将线段AD绕着点D顺时针旋转90°,得到线段DE,过点E作直线l⊥x轴,垂足为H,交抛物线于点F.
(1)求抛物线的表达式.
(2)连接DF,求∠EDF的正切值.
(3)点P在直线l上,且锐角∠EDP的正弦值为,求点P的坐标.
参考答案
1.A 2.B 3.C 4.D 5.C 6.D 7.C 8.D 9.B
10.D 提示:设DE与AC交于点F.
∵∠BAC=90°,点D是边BC的中点,
∴AD=BD=DC=BC.
∵DA=DB,
∴∠B=∠DAB.
∵∠ADE=∠B,
∴∠ADE=∠DAB,
∴AB∥DE,
∴∠BAC=∠DFC=90°.
∵DA=DC,
∴DE是AC的垂直平分线,
∴EA=EC.
∵EA=ED,
∴ED=EC,
∴∠EDC=∠ECD.
∵AB∥DE,
∴∠B=∠EDC,
∴∠DAB=∠ECD,
∴△DCE∽△BAD,
∴=.
∵∠BAC=90°,cos B==,
∴=3,
∴=3.
11. 12.75° 13.
14.(1)3(2分) (2)3或4(3分)
15.原式=-× 5分
=-1. 8分
16.解:在Rt△ABC中,∠C=90°,AC=2,AB=3,
∴BC===, 5分
∴sin A==. 8分
17.解:如图,作BE⊥CD于点E,
可得Rt△BED和矩形ACEB,
则有CE=AB=16,AC=BE. 2分
在Rt△BED中,∠DBE=45°,DE=BE=AC.
在Rt△DAC中,∠DAC=60°,DC=AC·tan 60°=AC. 4分
∵16+DE=DC,∴16+AC=AC,解得AC=8+8=DE,
∴CD=DE+CE=8+8+16=24+8. 7分
答:塔CD的高度为(24+8)米. 8分
18.解:如图,过点B作BM⊥FD于点M.
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=AC·tan 60°=10. 2分
∵AB∥CF,
∴BM=BC·sin 30°=10×=5,
CM=BC·cos 30°=15. 5分
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5,
∴CD=CM-MD=15-5. 8分
19.解:过点A作AG⊥EC,垂足为G,过点M作MN⊥AG,垂足为N,
则ME=NG,MN=EG.
∵MD=6 cm,DE=22 cm,
∴ME=NG=MD+DE=6+22=28(cm) 3分
在Rt△AMN中,∠AMN=37°,AM=10 cm,
∴AN=AM sin 37°≈10×=6(cm),
MN=AM cos 37°≈10×=8(cm),
∴MN=EG=8(cm),AG=AN+NG=6+28=34(cm) 6分
在Rt△AGC中,∠ACG=60°,
∴CG===≈19.61(cm),
∴EC=EG+CG=8+19.61≈27.6(cm),
∴EC的长约为27.6 cm. 10分
20.解:(1)∵斜坡的坡度为1∶3,∴=.
∵BD=CD-CB=2(米),
在Rt△ABD中,AB=3BD=6(米).
故AD==2≈6.4(米).
答:斜面AD的长度约为6.4米. 4分
(2)过C作CE⊥AD,垂足为E,
∴∠DCE+∠CDE=90°.
∵∠BAD+∠ADB=90°,
∴∠DCE=∠BAD,
∴tan∠BAD=tan∠DCE==. 6分
设DE=x米,则EC=3x米.
在Rt△CDE中,x2+(3x)2=32,即x==,
解得x≈0.94,
则3x=2.82.
∵2.82>2.8,
∴货车能进入地下停车场. 10分
21.解:(1)如图,延长CD、BA交于点E.
∵DC⊥BC,
∴∠BCE=90°.
∵tan∠ABC=,tan∠ABC=,
∴=. 2分
设CE=4k,则BC=3k.
∴BE===5k, 3分
∴cos∠ABC==, 4分
sin∠ABC==. 5分
(2)∵DA⊥BA,
∴∠E+∠ADE=90°.
∵DC⊥BC,
∴∠E+∠CBE=90°,
∴∠ADE=∠CBE,
∴cos∠ADE=cos∠CBE=. 7分
∵cos∠ADE=,∴=.
∵AD=3,∴DE=5,
∴CE=CD+DE=5+7=12. 9分
∵tan∠CBE=,tan∠CBE=,
∴=,∴BC=9,
∴BD===. 12分
22.解:(1)①如图1,
在△AMC和△CNB中,
∴△AMC≌△CNB,
∴AC=BC,∠ACM=∠CBN.
∵∠BCN+∠CBN=90°,
∴∠ACM+∠BCN=90°,
∴∠ACB=90°,
∴∠CAB=∠CBA=45°,
∴α+β=45°. 4分
②如图2,设正方形的边长为1,则CE=1,AE=2,BE=,
∴==,=,
=.
∵∠CEB=∠AEB,
∴△CEB∽△BEA,
∴∠CAB=∠CBE=α.
∵∠BED=∠ECB+∠CBE=α+β,
DE=DB,∠D=90°,∠BED=45°,
∴α+β=45°. 8分
(2)∠MON如图3所示,∠MOE=α,∠NOH=β, 10分
∴α-β=45°. 12分
23.解:(1)把点A(0,3),点B(5,0)代入y=-x2+bx+c,
得到解得
∴抛物线的解析式为y=-x2+x+3. 3分
(2)如图,过点E作EK⊥DF于点K.
∵∠AOD=∠ADE=∠DHE=90°,
∴∠ADO+∠OAD=90°,∠ADO+∠EDH=90°,
∴∠OAD=∠EDH. 4分
∵AD=DE,
∴△OAD≌△HDE(AAS),
∴EH=OD=1,DH=OA=3,
∴E(4,1). 5分
∵过点E作直线l⊥x轴,垂足为H,交抛物线y=-x2+x+3于点F,
∴F(4,3),
∴FH=3,
∴FH=DH=3.
∵∠DHE=90°,
∴∠DFH=45°,DF=3. 7分
∵EF=3-1=2,
∴KF=KE=,
∴DK=DF-KF=2.
在Rt△DKE中,tan∠EDF==. 8分
(3)①当点P在点E的上方时,
由锐角∠EDP的正弦值为,得∠EDP=45°.
又∵∠DFH=45°,∠DEP是公共角,
∴△EDF∽△EPD,
∴=,
∴ED2=EF EP.
设P(4,y),则EP=y-1.
又∵EF=2,ED==,
∴10=2(y-1),解得y=6,
∴点P的坐标为(4,6). 11分
②当点P在点E的下方时.
∵∠EDP=∠DFP=45°,∠DPF是公共角,
∴△PED∽△PDF,
∴=,
∴DP2=PE PF,
设P(4,y),则EP=1-y,FP=3-y,DP=,
∴9+y2=(1-y)(3-y),解得y=-.
∴点P的坐标为(4,-).
综上所述,当∠EDP=45°时,点P的坐标为(4,6)或(4,-). 14分
(时间:120分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.2tan 45°的值等于 ( )
A.2 B. C. D.1
2.如图,在Rt△ABC中,∠C=90°,AC=2,BC=3,则tan A的值为 ( )
A. B. C. D.
3.若cos A-=0,且∠A是锐角,则∠A的度数是 ( )
A.30° B.45°
C.60° D.90°
4.如图,在平面直角坐标系中,第一象限内射线OA与x轴正半轴的夹角为α,点P在射线OA上.若cos α=,则点P的坐标可能是 ( )
A.(3,5) B.(5,3)
C.(3,4) D.(4,3)
5.如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin ∠AOB的值等于 ( )
A. B.
C. D.
6.如图,某飞机在空中A处探测到它的正下方地平面上的目标C,此时飞机的飞行高度AC=1200 m,从飞机上看地平面指挥台B的俯角α=30°,则飞机A与指挥台B的距离为 ( )
A.1200 m B.1200 m
C.1200 m D.2400 m
7.如图,在△ABC中,AB=10,cos∠ABC=,D为边BC上一点,且AD=AC,若DC=4,则BD的值为 ( )
A.2 B.3
C.4 D.5
8.如图,在某次火箭发射过程中,火箭从地面到达A处时,在P处测得点A的仰角∠DPA为30°,且A与P两点的直线距离为10千米;当它沿铅垂线上升到达B处时,此时在P处测得点B的仰角∠DPB为45°,则从A处到B处的距离为(参考数据:≈1.7,≈1.4) ( )
A.1.5千米 B.2.0千米
C.2.5千米 D.3.5千米
9.图1是某公园的一个滑梯,图2是其示意图.滑梯的高BC为2 m,坡角∠A为60°,由于滑梯坡角过大存在安全隐患,公园管理局决定对滑梯进行整改,要在高度不变的前提下,通过加长滑梯的水平距离AB,使得坡角∠A满足30°≤∠A≤45°,则AB加长的距离可以是(参考数据:≈1.414,≈1.732) ( )
A.0.8 m B.1.6 m
C.2.4 m D.3.2 m
10.如图,在Rt△ABC中,∠BAC=90°,cos B=,D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使∠ADE=∠B,连接CE,则的值为 ( )
A. B.
C. D.3
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,已知CD=2,AC=3,则cos A= .
12.已知∠A,∠B,∠C是△ABC的三个内角,若|sin A-|+(cos B-)2=0,且∠A,∠B均为锐角,则∠C的度数为 .
13.如图,这是由边长相同的小正方形组成的网格,A、B、P、Q四点均在正方形网格的格点上,线段AB、PQ相交于点E,则tan∠AEP= .
14.如图,在Rt△ABC中,∠ABC=90°,AB=6,D是斜边AC上的一点,将△BCD沿BD翻折,使点C落到点C'处.
(1)若C'恰好是AB边的中点,则AC的长为 .
(2)若∠CBD=30°,连接AC',△ABC'正好是直角三角形,则BC的长为 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(π-)0-tan 60°·cos 30°.
16.如图,在Rt△ABC中,∠C=90°,AC=2,AB=3.求sin A的值.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,大楼AB的高为16米,远处有一塔CD,小李在楼底A处测得塔顶D处的仰角为60°,在楼顶B处测得塔顶D处的仰角为45°.其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,求塔CD的高度.
18.一副直角三角板按如图所示的方式放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
五、(本大题共2小题,每小题10分,满分20分)
19.张老师家的洗手盆上装有一种抬启式水龙头(如图1),水龙头完全开启后,把手AM与水平线的夹角为37°,此时把手端点A、出水口点B和落水点C在同一直线上.洗手盆及水龙头示意图如图2,其相关数据为AM=10 cm,MD=6 cm,DE=22 cm.求EC的长(结果精确到0.1 cm.参考数据:sin 37°≈,cos 37°≈,tan 37°≈,≈1.73).
20.西山公园要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的坡度为1∶3,一楼到地下停车场地面的垂直高度CD=3米,一楼到地平线的距离BC=1米.
(1)为保证斜坡的坡度为1∶3,斜面AD的长度应为多少米
(2)如果给该地下停车场送货的货车高度为2.8米,那么按这样的设计能保证货车顺利进入地下停车场吗 并说明理由.(参考数据:≈3.2)
六、(本题满分12分)
21.如图,tan ∠ABC=且DA⊥BA于点A,DC⊥BC于点C,DA=3,DC=7.
(1)求cos ∠ABC,sin ∠ABC的值.
(2)连接BD,求BD的长.
七、(本题满分12分)
22.数学老师布置了这样一个作业:
如果α,β都为锐角,且tan α=,tan β=,求α+β的度数.
甲、乙两位同学想利用正方形网格构图来解决问题,他们分别设计了图1和图2.
(1)请你分别利用图1、图2求出α+β的度数,并说明理由.
(2)请参考以上思考问题的方法,选择一种方法解决下面的问题.
如果α、β都为锐角,当tan α=5,tan β=时,在图3的正方形网格中,利用已作出的锐角α,画出∠MON,使得∠MON=α-β,直接写出α-β的度数,不必说明理由.
八、(本题满分14分)
23.在平面直角坐标系中,抛物线y=-x2+bx+c与y轴交于点A(0,3),与x轴的正半轴交于点B(5,0),点D在线段OB上,且OD=1,连接AD,将线段AD绕着点D顺时针旋转90°,得到线段DE,过点E作直线l⊥x轴,垂足为H,交抛物线于点F.
(1)求抛物线的表达式.
(2)连接DF,求∠EDF的正切值.
(3)点P在直线l上,且锐角∠EDP的正弦值为,求点P的坐标.
参考答案
1.A 2.B 3.C 4.D 5.C 6.D 7.C 8.D 9.B
10.D 提示:设DE与AC交于点F.
∵∠BAC=90°,点D是边BC的中点,
∴AD=BD=DC=BC.
∵DA=DB,
∴∠B=∠DAB.
∵∠ADE=∠B,
∴∠ADE=∠DAB,
∴AB∥DE,
∴∠BAC=∠DFC=90°.
∵DA=DC,
∴DE是AC的垂直平分线,
∴EA=EC.
∵EA=ED,
∴ED=EC,
∴∠EDC=∠ECD.
∵AB∥DE,
∴∠B=∠EDC,
∴∠DAB=∠ECD,
∴△DCE∽△BAD,
∴=.
∵∠BAC=90°,cos B==,
∴=3,
∴=3.
11. 12.75° 13.
14.(1)3(2分) (2)3或4(3分)
15.原式=-× 5分
=-1. 8分
16.解:在Rt△ABC中,∠C=90°,AC=2,AB=3,
∴BC===, 5分
∴sin A==. 8分
17.解:如图,作BE⊥CD于点E,
可得Rt△BED和矩形ACEB,
则有CE=AB=16,AC=BE. 2分
在Rt△BED中,∠DBE=45°,DE=BE=AC.
在Rt△DAC中,∠DAC=60°,DC=AC·tan 60°=AC. 4分
∵16+DE=DC,∴16+AC=AC,解得AC=8+8=DE,
∴CD=DE+CE=8+8+16=24+8. 7分
答:塔CD的高度为(24+8)米. 8分
18.解:如图,过点B作BM⊥FD于点M.
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=AC·tan 60°=10. 2分
∵AB∥CF,
∴BM=BC·sin 30°=10×=5,
CM=BC·cos 30°=15. 5分
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5,
∴CD=CM-MD=15-5. 8分
19.解:过点A作AG⊥EC,垂足为G,过点M作MN⊥AG,垂足为N,
则ME=NG,MN=EG.
∵MD=6 cm,DE=22 cm,
∴ME=NG=MD+DE=6+22=28(cm) 3分
在Rt△AMN中,∠AMN=37°,AM=10 cm,
∴AN=AM sin 37°≈10×=6(cm),
MN=AM cos 37°≈10×=8(cm),
∴MN=EG=8(cm),AG=AN+NG=6+28=34(cm) 6分
在Rt△AGC中,∠ACG=60°,
∴CG===≈19.61(cm),
∴EC=EG+CG=8+19.61≈27.6(cm),
∴EC的长约为27.6 cm. 10分
20.解:(1)∵斜坡的坡度为1∶3,∴=.
∵BD=CD-CB=2(米),
在Rt△ABD中,AB=3BD=6(米).
故AD==2≈6.4(米).
答:斜面AD的长度约为6.4米. 4分
(2)过C作CE⊥AD,垂足为E,
∴∠DCE+∠CDE=90°.
∵∠BAD+∠ADB=90°,
∴∠DCE=∠BAD,
∴tan∠BAD=tan∠DCE==. 6分
设DE=x米,则EC=3x米.
在Rt△CDE中,x2+(3x)2=32,即x==,
解得x≈0.94,
则3x=2.82.
∵2.82>2.8,
∴货车能进入地下停车场. 10分
21.解:(1)如图,延长CD、BA交于点E.
∵DC⊥BC,
∴∠BCE=90°.
∵tan∠ABC=,tan∠ABC=,
∴=. 2分
设CE=4k,则BC=3k.
∴BE===5k, 3分
∴cos∠ABC==, 4分
sin∠ABC==. 5分
(2)∵DA⊥BA,
∴∠E+∠ADE=90°.
∵DC⊥BC,
∴∠E+∠CBE=90°,
∴∠ADE=∠CBE,
∴cos∠ADE=cos∠CBE=. 7分
∵cos∠ADE=,∴=.
∵AD=3,∴DE=5,
∴CE=CD+DE=5+7=12. 9分
∵tan∠CBE=,tan∠CBE=,
∴=,∴BC=9,
∴BD===. 12分
22.解:(1)①如图1,
在△AMC和△CNB中,
∴△AMC≌△CNB,
∴AC=BC,∠ACM=∠CBN.
∵∠BCN+∠CBN=90°,
∴∠ACM+∠BCN=90°,
∴∠ACB=90°,
∴∠CAB=∠CBA=45°,
∴α+β=45°. 4分
②如图2,设正方形的边长为1,则CE=1,AE=2,BE=,
∴==,=,
=.
∵∠CEB=∠AEB,
∴△CEB∽△BEA,
∴∠CAB=∠CBE=α.
∵∠BED=∠ECB+∠CBE=α+β,
DE=DB,∠D=90°,∠BED=45°,
∴α+β=45°. 8分
(2)∠MON如图3所示,∠MOE=α,∠NOH=β, 10分
∴α-β=45°. 12分
23.解:(1)把点A(0,3),点B(5,0)代入y=-x2+bx+c,
得到解得
∴抛物线的解析式为y=-x2+x+3. 3分
(2)如图,过点E作EK⊥DF于点K.
∵∠AOD=∠ADE=∠DHE=90°,
∴∠ADO+∠OAD=90°,∠ADO+∠EDH=90°,
∴∠OAD=∠EDH. 4分
∵AD=DE,
∴△OAD≌△HDE(AAS),
∴EH=OD=1,DH=OA=3,
∴E(4,1). 5分
∵过点E作直线l⊥x轴,垂足为H,交抛物线y=-x2+x+3于点F,
∴F(4,3),
∴FH=3,
∴FH=DH=3.
∵∠DHE=90°,
∴∠DFH=45°,DF=3. 7分
∵EF=3-1=2,
∴KF=KE=,
∴DK=DF-KF=2.
在Rt△DKE中,tan∠EDF==. 8分
(3)①当点P在点E的上方时,
由锐角∠EDP的正弦值为,得∠EDP=45°.
又∵∠DFH=45°,∠DEP是公共角,
∴△EDF∽△EPD,
∴=,
∴ED2=EF EP.
设P(4,y),则EP=y-1.
又∵EF=2,ED==,
∴10=2(y-1),解得y=6,
∴点P的坐标为(4,6). 11分
②当点P在点E的下方时.
∵∠EDP=∠DFP=45°,∠DPF是公共角,
∴△PED∽△PDF,
∴=,
∴DP2=PE PF,
设P(4,y),则EP=1-y,FP=3-y,DP=,
∴9+y2=(1-y)(3-y),解得y=-.
∴点P的坐标为(4,-).
综上所述,当∠EDP=45°时,点P的坐标为(4,6)或(4,-). 14分
