第3章练习卷基础篇(单元测试)小学数学l六年级下册 人教版 (含答案)
文档属性
| 名称 | 第3章练习卷基础篇(单元测试)小学数学l六年级下册 人教版 (含答案) |  | |
| 格式 | Doc | ||
| 文件大小 | 167.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 20:16:40 | ||
图片预览




文档简介
(基础篇) 2023-2024学年下学期小学数学人教新版六年级第3章练习卷
一.选择题(共5小题)
1.一个圆柱如图。如果高增加2cm,那么这个圆柱的体积增加( )cm3。
A.2πr2h B.4πr2 C.2πr2 D.πr2(h+2)
2.把一个圆柱形的钢材削成一个最大的圆锥,圆锥体积是削去部分体积的( )
A. B. C. D.2倍
3.把一根长2米,直径2分米的圆柱木料锯成3段,表面积增加( )平方分米。
A.6.28 B.12.56 C.25.1 D.50.24
4.用一正方形纸围成一圆柱形(接口处忽略不算),这个圆柱( )相等。
A.底面直径和高 B.底面周长和高
C.底面积和侧面积 D.底面半径和高
5.一个圆柱,如果底面半径扩大到原来的3倍,高不变,那么它的侧面积扩大到原来的( )
A.3倍 B.6倍 C.9倍
二.填空题(共5小题)
6.把一个圆柱形木料削成一个等底、等高的圆锥,削去部分的体积是2.4dm3。这根圆柱形木料的体积是 dm3,削成的圆锥的体积是 dm3。
7.如图,有一张长方形铁皮,按下面方式进行裁切后,可以做成一个圆柱,那么做成的圆柱的侧面积是 。
8.一个圆柱形木料,底面半径是2dm,高是3dm,它的表面积是 dm2,若削成一个最大的圆锥形模具,这个模具所占的空间是 dm3。
9.一个圆柱与一个圆锥等底等高,体积相差24立方厘米,那么圆锥的体积是 立方厘米,圆柱的体积是 立方厘米。
10.把棱长1cm的正方体木块,削成一个最大的圆柱,圆柱的体积是 。
三.判断题(共5小题)
11.一个圆柱的底面积是12.56平方厘米,高是12.6厘米,这个圆柱的侧面展开图是正方形。
12.一个圆锥的体积和一个圆柱的体积相等,圆锥的高是圆柱高的3倍。
13.把一块圆柱形钢材削成一块最大圆锥形钢材,削掉部分的重量是35千克,削得的圆锥形钢材的重量是17.5千克。
14.圆锥的高不变,底面半径缩小到原来的,则体积缩小到原来的。
15.圆锥的体积等于圆柱体积的三分之一. .
四.计算题(共2小题)
16.计算如图圆锥的体积.
17.已知:直角三角形如图所示,若以AC为轴旋转一周得一个几何体,求这个几何体的体积.
五.应用题(共5小题)
18.丽丽有一个圆柱形水壶,从内部测量,水壶底面直径为10cm,高为20cm,丽丽每天上学带一整壶水,正好喝完,丽丽每天喝多少毫升水?
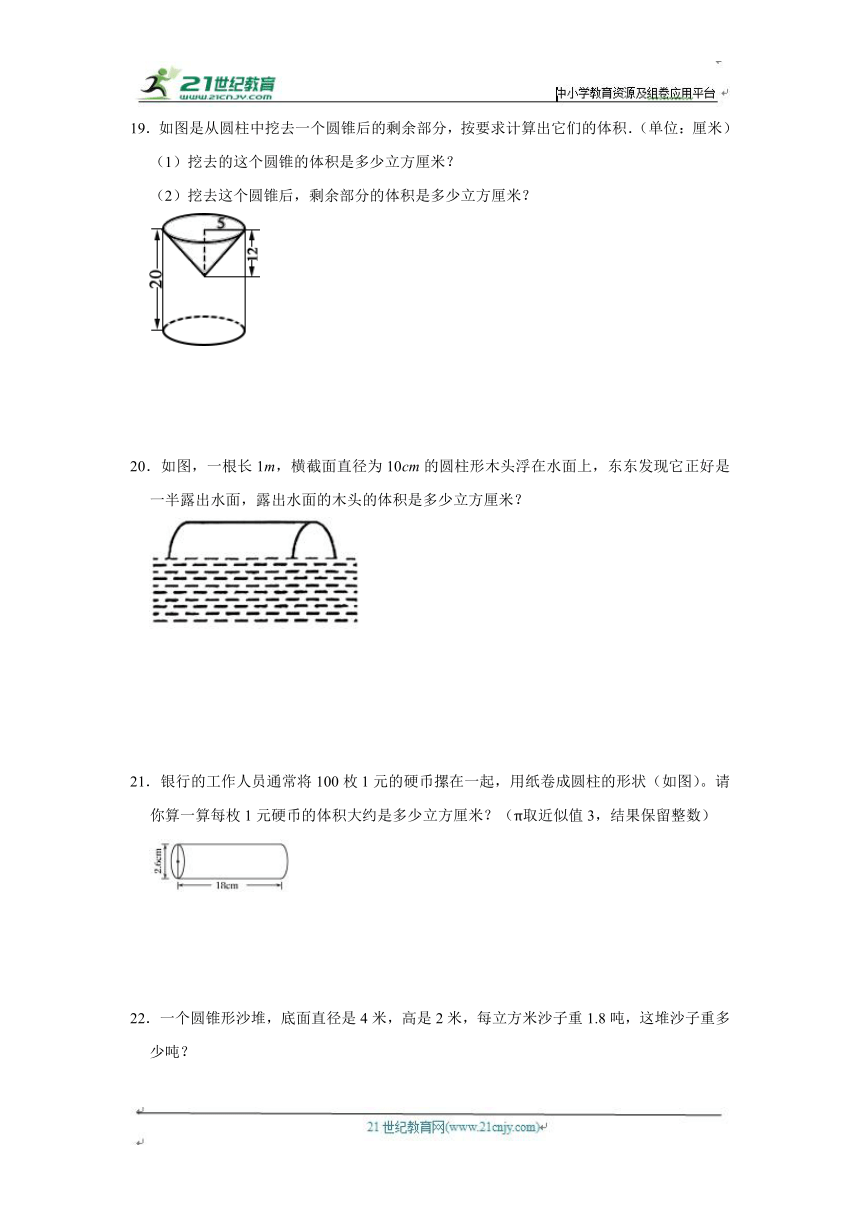
19.如图是从圆柱中挖去一个圆锥后的剩余部分,按要求计算出它们的体积.(单位:厘米)
(1)挖去的这个圆锥的体积是多少立方厘米?
(2)挖去这个圆锥后,剩余部分的体积是多少立方厘米?
20.如图,一根长1m,横截面直径为10cm的圆柱形木头浮在水面上,东东发现它正好是一半露出水面,露出水面的木头的体积是多少立方厘米?
21.银行的工作人员通常将100枚1元的硬币摞在一起,用纸卷成圆柱的形状(如图)。请你算一算每枚1元硬币的体积大约是多少立方厘米?(π取近似值3,结果保留整数)
22.一个圆锥形沙堆,底面直径是4米,高是2米,每立方米沙子重1.8吨,这堆沙子重多少吨?
(基础篇) 2023-2024学年下学期小学数学人教新版六年级第3章练习卷
参考答案与试题解析
一.选择题(共5小题)
1.一个圆柱如图。如果高增加2cm,那么这个圆柱的体积增加( )cm3。
A.2πr2h B.4πr2 C.2πr2 D.πr2(h+2)
【解答】解:一个圆柱如图。如果高增加2cm,那么这个圆柱的体积增加2πr2cm3。
故选:C。
2.把一个圆柱形的钢材削成一个最大的圆锥,圆锥体积是削去部分体积的( )
A. B. C. D.2倍
【解答】解:1÷(3﹣1)=;
故选:C.
3.把一根长2米,直径2分米的圆柱木料锯成3段,表面积增加( )平方分米。
A.6.28 B.12.56 C.25.1 D.50.24
【解答】解:(3﹣1)×2
=2×2
=4(个)
3.14×(2÷2)2×4
=3.14×4
=12.56(平方分米)
答:表面积增加12.56平方分米。
故选:B。
4.用一正方形纸围成一圆柱形(接口处忽略不算),这个圆柱( )相等。
A.底面直径和高 B.底面周长和高
C.底面积和侧面积 D.底面半径和高
【解答】解:用一正方形纸围成一圆柱形(接口处忽略不算),这个圆柱底面周长和高相等。
故选:B。
5.一个圆柱,如果底面半径扩大到原来的3倍,高不变,那么它的侧面积扩大到原来的( )
A.3倍 B.6倍 C.9倍
【解答】解:因为圆柱侧面积=2π×圆柱底面半径×高,
圆柱底面半径扩大到原来的3倍,高不变,侧面积就扩大3倍.
故选:A。
二.填空题(共5小题)
6.把一个圆柱形木料削成一个等底、等高的圆锥,削去部分的体积是2.4dm3。这根圆柱形木料的体积是 3.6 dm3,削成的圆锥的体积是 1.2 dm3。
【解答】解:圆锥的体积是:2.4÷2=1.2(dm3)
圆柱的体积是:1.2×3=3.6(dm3)
答:这根圆柱形木料的体积是3.6dm3,削成的圆锥的体积是1.2dm3。
故答案为:3.6;1.2。
7.如图,有一张长方形铁皮,按下面方式进行裁切后,可以做成一个圆柱,那么做成的圆柱的侧面积是 50.24平方厘米 。
【解答】解:3.14×2×2×(2×2)
=6.28×2×4
=12.56×4
=50.24(cm2)
答:做成的圆柱的侧面积是50.24cm2。
故答案为:50.24平方厘米。
8.一个圆柱形木料,底面半径是2dm,高是3dm,它的表面积是 62.8 dm2,若削成一个最大的圆锥形模具,这个模具所占的空间是 12.56 dm3。
【解答】解:圆柱的表面积:
2×3.14×2×3+3.14×22×2
=37.68+25.12
=62.8(dm2)
圆锥的体积:
×3.14×22×3
=×3.14×4×3
=12.56(dm3)
答:圆柱的表面积是62.8dm2,若削成一个最大的圆锥形模具,这个模具所占的空间是12.56dm3。
故答案为:62.8;12.56。
9.一个圆柱与一个圆锥等底等高,体积相差24立方厘米,那么圆锥的体积是 12 立方厘米,圆柱的体积是 36 立方厘米。
【解答】解:24÷(3﹣1)
=24÷2
=12(立方厘米)
12×3=36(立方厘米)
答:因锥的体积是12立方厘米,圆柱的体积是36立方厘米。
故答案为:12,36。
10.把棱长1cm的正方体木块,削成一个最大的圆柱,圆柱的体积是 0.785立方厘米 。
【解答】解:3.14×(1÷2)2×1
=3.14×0.25×1
=0.785(立方厘米)
答:圆柱的体积是0.785立方厘米。
故答案为:0.785立方厘米。
三.判断题(共5小题)
11.一个圆柱的底面积是12.56平方厘米,高是12.6厘米,这个圆柱的侧面展开图是正方形。 √
【解答】解:12.56÷3.14=4(平方厘米)
则底面半径为2厘米;侧面展开后长方形的长(底面周长):2πr=2×3.14×2=12.56(厘米)
而高12.56厘米;所以这个圆柱的侧面展开是正方形。题干说法正确。
故答案为:√。
12.一个圆锥的体积和一个圆柱的体积相等,圆锥的高是圆柱高的3倍。 ×
【解答】解:一个圆锥的体积和一个圆柱的体积相等,在没有确定圆锥的底面积与圆柱的底面积是否相等时,就无法确定圆锥的高是圆柱高的3倍。
因此题干中的结论是错误的。
故答案为:×。
13.把一块圆柱形钢材削成一块最大圆锥形钢材,削掉部分的重量是35千克,削得的圆锥形钢材的重量是17.5千克。 √
【解答】解:35÷(3﹣1)
=35÷2
=17.5(千克)
所以削得的圆锥形钢材的重量是17.5千克。
因此题干中的结论是正确的。
故答案为:√。
14.圆锥的高不变,底面半径缩小到原来的,则体积缩小到原来的。 √
【解答】解:由题意得,圆锥的高不变,底面半径缩小到原来的,则体积缩小到原来的,原说法正确。
故答案为:√。
15.圆锥的体积等于圆柱体积的三分之一. × .
【解答】解:圆锥的体积等于圆柱体积的三分之一是错误的,只有在圆锥、圆柱等底、等高的情况下,圆锥的体积等于圆柱体积的三分之一.
故答案为:×.
四.计算题(共2小题)
16.计算如图圆锥的体积.
【解答】解:3.14×(4÷2)2×4.5
=3.14×4×4.5
=18.84(立方厘米)
答:这个圆锥的体积是18.84立方厘米.
17.已知:直角三角形如图所示,若以AC为轴旋转一周得一个几何体,求这个几何体的体积.
【解答】解:×3.14×32×4
=3.14×3×4
=37.68
答:这个圆锥体的体积是37.68.
五.应用题(共5小题)
18.丽丽有一个圆柱形水壶,从内部测量,水壶底面直径为10cm,高为20cm,丽丽每天上学带一整壶水,正好喝完,丽丽每天喝多少毫升水?
【解答】解:3.14×(10÷2)2×20
=3.14×25×20
=1570(立方厘米)
1570立方厘米=1570毫升
答:丽丽每天喝1570毫升水。
19.如图是从圆柱中挖去一个圆锥后的剩余部分,按要求计算出它们的体积.(单位:厘米)
(1)挖去的这个圆锥的体积是多少立方厘米?
(2)挖去这个圆锥后,剩余部分的体积是多少立方厘米?
【解答】解:(1)×3.14×52×12
=×942
=314(立方厘米)
答:挖去的这个圆锥的体积是314立方厘米.
(2)3.14×52×20﹣314
=1570﹣314
=1256(立方厘米)
答:挖去这个圆锥后,剩余部分的体积是1256立方厘米.
20.如图,一根长1m,横截面直径为10cm的圆柱形木头浮在水面上,东东发现它正好是一半露出水面,露出水面的木头的体积是多少立方厘米?
【解答】解:1米=100厘米
3.14×(10÷2)2×100÷2
=3.14×25×100÷2
=7850÷2
=3925(立方厘米)
答:露出水面的木头的体积是3925立方厘米。
3925立方厘米。
21.银行的工作人员通常将100枚1元的硬币摞在一起,用纸卷成圆柱的形状(如图)。请你算一算每枚1元硬币的体积大约是多少立方厘米?(π取近似值3,结果保留整数)
【解答】解:18÷100=0.18(厘米)
3×(2.6÷2)2×0.18
=3×1.32×0.18
=3×1.69×0.18
≈1(立方厘米)
答:每枚1元的硬币的体积大约是1立方厘米。
22.一个圆锥形沙堆,底面直径是4米,高是2米,每立方米沙子重1.8吨,这堆沙子重多少吨?
【解答】解:×3.14×(4÷2)2×2×1.8
=3.14×22×2×1.8
=15.072(吨)
答:这堆沙子重15.072吨.
一.选择题(共5小题)
1.一个圆柱如图。如果高增加2cm,那么这个圆柱的体积增加( )cm3。
A.2πr2h B.4πr2 C.2πr2 D.πr2(h+2)
2.把一个圆柱形的钢材削成一个最大的圆锥,圆锥体积是削去部分体积的( )
A. B. C. D.2倍
3.把一根长2米,直径2分米的圆柱木料锯成3段,表面积增加( )平方分米。
A.6.28 B.12.56 C.25.1 D.50.24
4.用一正方形纸围成一圆柱形(接口处忽略不算),这个圆柱( )相等。
A.底面直径和高 B.底面周长和高
C.底面积和侧面积 D.底面半径和高
5.一个圆柱,如果底面半径扩大到原来的3倍,高不变,那么它的侧面积扩大到原来的( )
A.3倍 B.6倍 C.9倍
二.填空题(共5小题)
6.把一个圆柱形木料削成一个等底、等高的圆锥,削去部分的体积是2.4dm3。这根圆柱形木料的体积是 dm3,削成的圆锥的体积是 dm3。
7.如图,有一张长方形铁皮,按下面方式进行裁切后,可以做成一个圆柱,那么做成的圆柱的侧面积是 。
8.一个圆柱形木料,底面半径是2dm,高是3dm,它的表面积是 dm2,若削成一个最大的圆锥形模具,这个模具所占的空间是 dm3。
9.一个圆柱与一个圆锥等底等高,体积相差24立方厘米,那么圆锥的体积是 立方厘米,圆柱的体积是 立方厘米。
10.把棱长1cm的正方体木块,削成一个最大的圆柱,圆柱的体积是 。
三.判断题(共5小题)
11.一个圆柱的底面积是12.56平方厘米,高是12.6厘米,这个圆柱的侧面展开图是正方形。
12.一个圆锥的体积和一个圆柱的体积相等,圆锥的高是圆柱高的3倍。
13.把一块圆柱形钢材削成一块最大圆锥形钢材,削掉部分的重量是35千克,削得的圆锥形钢材的重量是17.5千克。
14.圆锥的高不变,底面半径缩小到原来的,则体积缩小到原来的。
15.圆锥的体积等于圆柱体积的三分之一. .
四.计算题(共2小题)
16.计算如图圆锥的体积.
17.已知:直角三角形如图所示,若以AC为轴旋转一周得一个几何体,求这个几何体的体积.
五.应用题(共5小题)
18.丽丽有一个圆柱形水壶,从内部测量,水壶底面直径为10cm,高为20cm,丽丽每天上学带一整壶水,正好喝完,丽丽每天喝多少毫升水?
19.如图是从圆柱中挖去一个圆锥后的剩余部分,按要求计算出它们的体积.(单位:厘米)
(1)挖去的这个圆锥的体积是多少立方厘米?
(2)挖去这个圆锥后,剩余部分的体积是多少立方厘米?
20.如图,一根长1m,横截面直径为10cm的圆柱形木头浮在水面上,东东发现它正好是一半露出水面,露出水面的木头的体积是多少立方厘米?
21.银行的工作人员通常将100枚1元的硬币摞在一起,用纸卷成圆柱的形状(如图)。请你算一算每枚1元硬币的体积大约是多少立方厘米?(π取近似值3,结果保留整数)
22.一个圆锥形沙堆,底面直径是4米,高是2米,每立方米沙子重1.8吨,这堆沙子重多少吨?
(基础篇) 2023-2024学年下学期小学数学人教新版六年级第3章练习卷
参考答案与试题解析
一.选择题(共5小题)
1.一个圆柱如图。如果高增加2cm,那么这个圆柱的体积增加( )cm3。
A.2πr2h B.4πr2 C.2πr2 D.πr2(h+2)
【解答】解:一个圆柱如图。如果高增加2cm,那么这个圆柱的体积增加2πr2cm3。
故选:C。
2.把一个圆柱形的钢材削成一个最大的圆锥,圆锥体积是削去部分体积的( )
A. B. C. D.2倍
【解答】解:1÷(3﹣1)=;
故选:C.
3.把一根长2米,直径2分米的圆柱木料锯成3段,表面积增加( )平方分米。
A.6.28 B.12.56 C.25.1 D.50.24
【解答】解:(3﹣1)×2
=2×2
=4(个)
3.14×(2÷2)2×4
=3.14×4
=12.56(平方分米)
答:表面积增加12.56平方分米。
故选:B。
4.用一正方形纸围成一圆柱形(接口处忽略不算),这个圆柱( )相等。
A.底面直径和高 B.底面周长和高
C.底面积和侧面积 D.底面半径和高
【解答】解:用一正方形纸围成一圆柱形(接口处忽略不算),这个圆柱底面周长和高相等。
故选:B。
5.一个圆柱,如果底面半径扩大到原来的3倍,高不变,那么它的侧面积扩大到原来的( )
A.3倍 B.6倍 C.9倍
【解答】解:因为圆柱侧面积=2π×圆柱底面半径×高,
圆柱底面半径扩大到原来的3倍,高不变,侧面积就扩大3倍.
故选:A。
二.填空题(共5小题)
6.把一个圆柱形木料削成一个等底、等高的圆锥,削去部分的体积是2.4dm3。这根圆柱形木料的体积是 3.6 dm3,削成的圆锥的体积是 1.2 dm3。
【解答】解:圆锥的体积是:2.4÷2=1.2(dm3)
圆柱的体积是:1.2×3=3.6(dm3)
答:这根圆柱形木料的体积是3.6dm3,削成的圆锥的体积是1.2dm3。
故答案为:3.6;1.2。
7.如图,有一张长方形铁皮,按下面方式进行裁切后,可以做成一个圆柱,那么做成的圆柱的侧面积是 50.24平方厘米 。
【解答】解:3.14×2×2×(2×2)
=6.28×2×4
=12.56×4
=50.24(cm2)
答:做成的圆柱的侧面积是50.24cm2。
故答案为:50.24平方厘米。
8.一个圆柱形木料,底面半径是2dm,高是3dm,它的表面积是 62.8 dm2,若削成一个最大的圆锥形模具,这个模具所占的空间是 12.56 dm3。
【解答】解:圆柱的表面积:
2×3.14×2×3+3.14×22×2
=37.68+25.12
=62.8(dm2)
圆锥的体积:
×3.14×22×3
=×3.14×4×3
=12.56(dm3)
答:圆柱的表面积是62.8dm2,若削成一个最大的圆锥形模具,这个模具所占的空间是12.56dm3。
故答案为:62.8;12.56。
9.一个圆柱与一个圆锥等底等高,体积相差24立方厘米,那么圆锥的体积是 12 立方厘米,圆柱的体积是 36 立方厘米。
【解答】解:24÷(3﹣1)
=24÷2
=12(立方厘米)
12×3=36(立方厘米)
答:因锥的体积是12立方厘米,圆柱的体积是36立方厘米。
故答案为:12,36。
10.把棱长1cm的正方体木块,削成一个最大的圆柱,圆柱的体积是 0.785立方厘米 。
【解答】解:3.14×(1÷2)2×1
=3.14×0.25×1
=0.785(立方厘米)
答:圆柱的体积是0.785立方厘米。
故答案为:0.785立方厘米。
三.判断题(共5小题)
11.一个圆柱的底面积是12.56平方厘米,高是12.6厘米,这个圆柱的侧面展开图是正方形。 √
【解答】解:12.56÷3.14=4(平方厘米)
则底面半径为2厘米;侧面展开后长方形的长(底面周长):2πr=2×3.14×2=12.56(厘米)
而高12.56厘米;所以这个圆柱的侧面展开是正方形。题干说法正确。
故答案为:√。
12.一个圆锥的体积和一个圆柱的体积相等,圆锥的高是圆柱高的3倍。 ×
【解答】解:一个圆锥的体积和一个圆柱的体积相等,在没有确定圆锥的底面积与圆柱的底面积是否相等时,就无法确定圆锥的高是圆柱高的3倍。
因此题干中的结论是错误的。
故答案为:×。
13.把一块圆柱形钢材削成一块最大圆锥形钢材,削掉部分的重量是35千克,削得的圆锥形钢材的重量是17.5千克。 √
【解答】解:35÷(3﹣1)
=35÷2
=17.5(千克)
所以削得的圆锥形钢材的重量是17.5千克。
因此题干中的结论是正确的。
故答案为:√。
14.圆锥的高不变,底面半径缩小到原来的,则体积缩小到原来的。 √
【解答】解:由题意得,圆锥的高不变,底面半径缩小到原来的,则体积缩小到原来的,原说法正确。
故答案为:√。
15.圆锥的体积等于圆柱体积的三分之一. × .
【解答】解:圆锥的体积等于圆柱体积的三分之一是错误的,只有在圆锥、圆柱等底、等高的情况下,圆锥的体积等于圆柱体积的三分之一.
故答案为:×.
四.计算题(共2小题)
16.计算如图圆锥的体积.
【解答】解:3.14×(4÷2)2×4.5
=3.14×4×4.5
=18.84(立方厘米)
答:这个圆锥的体积是18.84立方厘米.
17.已知:直角三角形如图所示,若以AC为轴旋转一周得一个几何体,求这个几何体的体积.
【解答】解:×3.14×32×4
=3.14×3×4
=37.68
答:这个圆锥体的体积是37.68.
五.应用题(共5小题)
18.丽丽有一个圆柱形水壶,从内部测量,水壶底面直径为10cm,高为20cm,丽丽每天上学带一整壶水,正好喝完,丽丽每天喝多少毫升水?
【解答】解:3.14×(10÷2)2×20
=3.14×25×20
=1570(立方厘米)
1570立方厘米=1570毫升
答:丽丽每天喝1570毫升水。
19.如图是从圆柱中挖去一个圆锥后的剩余部分,按要求计算出它们的体积.(单位:厘米)
(1)挖去的这个圆锥的体积是多少立方厘米?
(2)挖去这个圆锥后,剩余部分的体积是多少立方厘米?
【解答】解:(1)×3.14×52×12
=×942
=314(立方厘米)
答:挖去的这个圆锥的体积是314立方厘米.
(2)3.14×52×20﹣314
=1570﹣314
=1256(立方厘米)
答:挖去这个圆锥后,剩余部分的体积是1256立方厘米.
20.如图,一根长1m,横截面直径为10cm的圆柱形木头浮在水面上,东东发现它正好是一半露出水面,露出水面的木头的体积是多少立方厘米?
【解答】解:1米=100厘米
3.14×(10÷2)2×100÷2
=3.14×25×100÷2
=7850÷2
=3925(立方厘米)
答:露出水面的木头的体积是3925立方厘米。
3925立方厘米。
21.银行的工作人员通常将100枚1元的硬币摞在一起,用纸卷成圆柱的形状(如图)。请你算一算每枚1元硬币的体积大约是多少立方厘米?(π取近似值3,结果保留整数)
【解答】解:18÷100=0.18(厘米)
3×(2.6÷2)2×0.18
=3×1.32×0.18
=3×1.69×0.18
≈1(立方厘米)
答:每枚1元的硬币的体积大约是1立方厘米。
22.一个圆锥形沙堆,底面直径是4米,高是2米,每立方米沙子重1.8吨,这堆沙子重多少吨?
【解答】解:×3.14×(4÷2)2×2×1.8
=3.14×22×2×1.8
=15.072(吨)
答:这堆沙子重15.072吨.
