第3章练习卷培优篇(单元测试)小学数学六年级下册 人教版 (含答案)
文档属性
| 名称 | 第3章练习卷培优篇(单元测试)小学数学六年级下册 人教版 (含答案) |
|
|
| 格式 | Doc | ||
| 文件大小 | 210.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 00:00:00 | ||
图片预览




文档简介
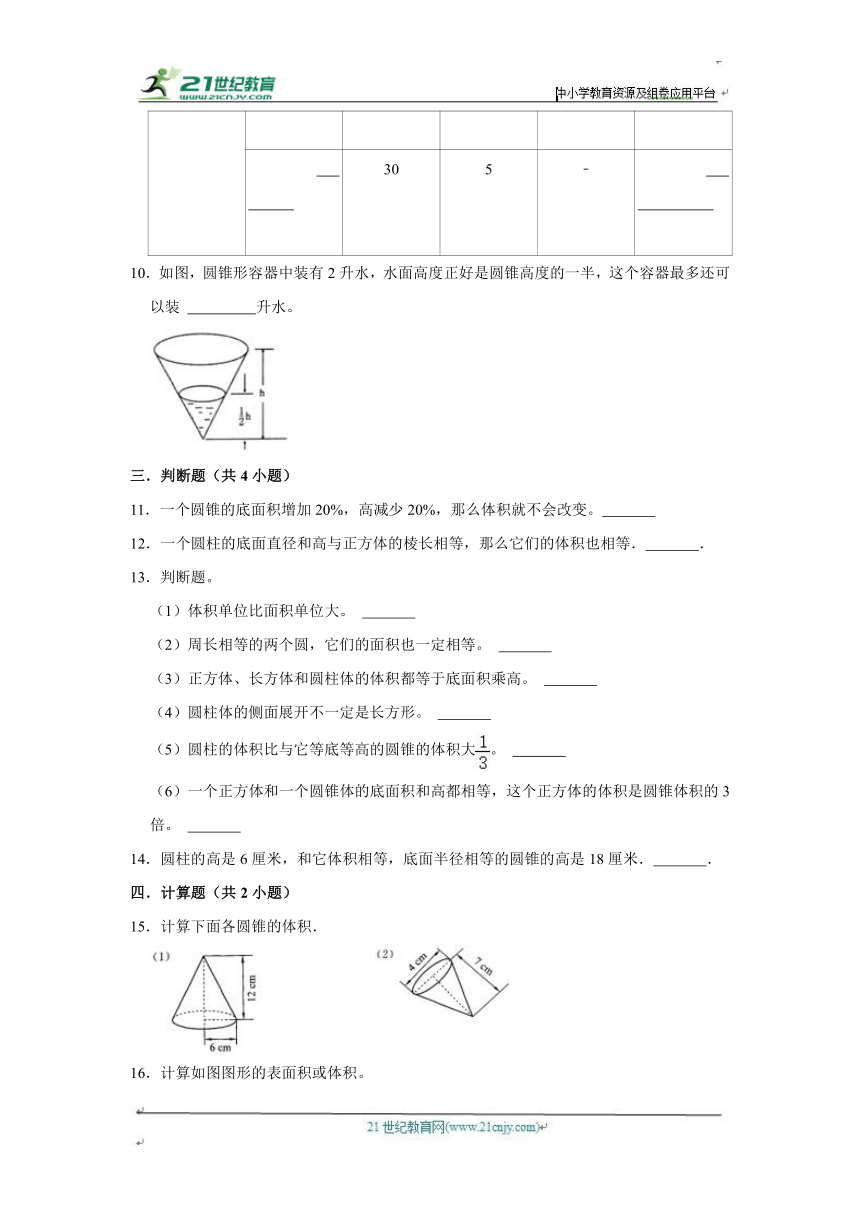
(培优篇) 2023-2024学年下学期小学数学人教新版六年级第3章练习卷
一.选择题(共5小题)
1.右图中,瓶底的面积和锥形杯口的面积相等,将瓶子中的液体倒入锥形杯子、能倒满( )杯。
A.2 B.3 C.4 D.6
2.一个圆柱侧面展开是正方形,这个圆柱的底面半径是1分米,高是( )分米。
A.1 B.2 C.6.28
3.下面各图形以虚线为轴旋转一周形成几何体,( )图形成的体积与如图形成的体积相等。
A. B.
C. D.
4.把一块圆柱形铁块熔铸成与它等高的圆锥,底面积将( )
A.扩大到原来的3倍 B.缩小到原来的
C.与原来一样
5.一个高5cm,半径2cm的圆柱木料,将它锯成完全相同的两部分后,表面积可能增加了( )cm2。
A.20 B.40 C.12.56
二.填空题(共5小题)
6.把长2米的圆柱体原木切成大小一样的3个小圆柱之后,表面积增加了12.56cm2,这个圆柱体木头原来的表面积是 cm2,体积是 dm3。
7.如图是一个由圆柱和圆锥组成的陀螺,圆柱和圆锥的底面积相等,圆锥的高是圆柱高的。圆柱的体积是180立方厘米,陀螺的体积是 立方厘米。
8.一根长1米,横截面直径是20厘米的木头浮在水面上,小明发现它正好是一半露出水面,请你求出这根木头与水接触的面的面积是 平方厘米.
9.算一算,填一填。
名称 底面半径/cm 底面直径/cm 高/cm 表面积/cm2 体积/cm3
圆柱 10 4
4 10
圆锥 2 0.9 ﹣
30 5 ﹣
10.如图,圆锥形容器中装有2升水,水面高度正好是圆锥高度的一半,这个容器最多还可以装 升水。
三.判断题(共4小题)
11.一个圆锥的底面积增加20%,高减少20%,那么体积就不会改变。
12.一个圆柱的底面直径和高与正方体的棱长相等,那么它们的体积也相等. .
13.判断题。
(1)体积单位比面积单位大。
(2)周长相等的两个圆,它们的面积也一定相等。
(3)正方体、长方体和圆柱体的体积都等于底面积乘高。
(4)圆柱体的侧面展开不一定是长方形。
(5)圆柱的体积比与它等底等高的圆锥的体积大。
(6)一个正方体和一个圆锥体的底面积和高都相等,这个正方体的体积是圆锥体积的3倍。
14.圆柱的高是6厘米,和它体积相等,底面半径相等的圆锥的高是18厘米. .
四.计算题(共2小题)
15.计算下面各圆锥的体积.
16.计算如图图形的表面积或体积。
(1)求表面积。(单位:cm)
(2)求体积。(单位:cm)
五.应用题(共4小题)
17.一个圆柱形水杯的容积是3.6升,底面积是1.2平方分米,装了杯水,水面离杯口高多少分米?
18.把一个底面周长是31.4分米,高9分米的圆柱体铁块熔铸成一个底面半径是6分米的圆锥体,圆锥的高是多少分米?
19.一个圆柱,如果高减少2厘米,表面积就减少25.12平方厘米,体积减少.这个圆柱原来的体积是多少立方厘米?
20.一个无盖的圆柱形铁皮水桶,高50厘米,底面直径40厘米,做这个水桶至少需要多少平方厘米的铁皮?
21.一个圆锥形沙堆,底面直径是8米,高是1.8米.它的体积大约是多少立方米?
22.用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:厘米),打结处正好是底面圆心,打结用去绳长25厘米.扎这个盒子至少用去塑料绳多少厘米?在它的整个侧面贴上商标和说明,这部分的面积是多少平方厘米?
(培优篇) 2023-2024学年下学期小学数学人教新版六年级第3章练习卷
参考答案与试题解析
一.选择题(共5小题)
1.右图中,瓶底的面积和锥形杯口的面积相等,将瓶子中的液体倒入锥形杯子、能倒满( )杯。
A.2 B.3 C.4 D.6
【解答】解:3×2=6
答:能装满6杯。
故选:D。
2.一个圆柱侧面展开是正方形,这个圆柱的底面半径是1分米,高是( )分米。
A.1 B.2 C.6.28
【解答】解:2×3.14×1=6.28(分米)
答:高是6.28分米。
故选:C。
3.下面各图形以虚线为轴旋转一周形成几何体,( )图形成的体积与如图形成的体积相等。
A. B.
C. D.
【解答】解:π×22×6×=8π(cm3)
A、π×22×2=8π(cm3)
B、π×22×3=12π(cm3)
C、π×32×2=18π(cm3)
D、×π×62×2=24π(cm3)
故选:A。
4.把一块圆柱形铁块熔铸成与它等高的圆锥,底面积将( )
A.扩大到原来的3倍 B.缩小到原来的
C.与原来一样
【解答】解:把一块圆柱形铁块熔铸成与它等高的圆锥,底面积将扩大到原来的3倍。
故选:A。
5.一个高5cm,半径2cm的圆柱木料,将它锯成完全相同的两部分后,表面积可能增加了( )cm2。
A.20 B.40 C.12.56
【解答】解:5×2×2×2
=5×8
=40(平方厘米)
答:表面积可能增加了40cm2。
故选:B。
二.填空题(共5小题)
6.把长2米的圆柱体原木切成大小一样的3个小圆柱之后,表面积增加了12.56cm2,这个圆柱体木头原来的表面积是 1262.28 cm2,体积是 628 dm3。
【解答】解:12.56÷4=3.14(平方厘米)
3.14÷3.14=1(厘米)
2米=200厘米
3.14×2+3.14×1×2×200
=6.28+1256
=1262.28(平方厘米)
3.14×200=628(立方厘米)
答:这个圆柱体木头原来的表面积是1262.28cm2,体积是628dm3。
故答案为:1262.28,628。
7.如图是一个由圆柱和圆锥组成的陀螺,圆柱和圆锥的底面积相等,圆锥的高是圆柱高的。圆柱的体积是180立方厘米,陀螺的体积是 210 立方厘米。
【解答】解:180××
=60×
=30(立方厘米)
180+30=210(立方厘米)
答:陀螺的体积是210立方厘米。
故答案为:210。
8.一根长1米,横截面直径是20厘米的木头浮在水面上,小明发现它正好是一半露出水面,请你求出这根木头与水接触的面的面积是 3454 平方厘米.
【解答】解:木头横截面的半径为:20÷2=10(厘米),
两个底面积:3.14×102×2=628(平方厘米),
侧面积:3.14×20×100
=62.8×100,
=6280(平方厘米),
表面积:628+6280=6908(平方厘米),
与水接触的面积:6908÷2=3454(平方厘米)
答:这根木头与水接触的面的面积是3454平方厘米.
故答案为:3454.
9.算一算,填一填。
名称 底面半径/cm 底面直径/cm 高/cm 表面积/cm2 体积/cm3
圆柱 10 20 4 879.2 1256
2 4 10 150.72 125.6
圆锥 2 4 0.9 ﹣ 3.768
15 30 5 ﹣ 1177.5
【解答】解:10×2=20(厘米)
2×3.14×10×4+3.14×102×2
=62.8×4+3.14×100×2
=251.2+628
=879.2(平方厘米)
3.14×102×4
=3.14×100×4
=314×4
=1256(立方厘米)
4÷2=2(厘米)
3.14×4×10+3.14×22×2
=12.56×10+3.14×4×2
=125.6+25.12
=150.72(立方厘米)
3.14×22×10
=3.14×4×10
=125.6(立方厘米)
2×2=4(厘米)
×3.14×22×0.9
=×3.14×4×0.9
=3.768(立方厘米)
30÷2=15(厘米)
×3.14×152×5
=3.14×225×5
=1177.5(立方厘米)
填表如下:
名称 底面半径/cm 底面直径/cm 高/cm 表面积/cm2 体积/cm3
圆柱 10 20 4 879.2 1256
2 4 10 150.72 125.6
圆锥 2 4 0.9 ﹣ 3.768
15 30 5 ﹣ 1177.5
故答案为:20、879.2、1256;2、150.72、125.6;4、3.768;15、1177.5。
10.如图,圆锥形容器中装有2升水,水面高度正好是圆锥高度的一半,这个容器最多还可以装 14 升水。
【解答】解:如图:
可设容器中水的底面积为S1,圆锥形容器的底面积为S。
S1:S=()2:h2=1:4,即S=4S1
水的体积:
2=S1×=12
容器的容积:
Sh=×4S1
=×4×12
=16(升)
16﹣2=14(升)
答:这个容器还能装14升水。
故答案为:14。
三.判断题(共4小题)
11.一个圆锥的底面积增加20%,高减少20%,那么体积就不会改变。 ×
【解答】解:设原来圆锥的底面积为S,高为h,
原来的体积是:V=Sh
锥的底面积增加20%,高减少20%,
则变化后圆锥的体积为:V=×1.2S×0.8h
=0.32Sh
0.32Sh≠Sh
因此,一个圆锥的底面积增加20%,高减少20%,那么体积就不会改变。这种说法是错误的。
故答案为:×。
12.一个圆柱的底面直径和高与正方体的棱长相等,那么它们的体积也相等. × .
【解答】解:由圆柱和正方体的体积公式可知,一个圆柱和一个正方体的底面积和高相等,那么它们的体积也相等;
但这里圆柱的底面积与正方体的底面积不一定相等.
故答案为:×.
13.判断题。
(1)体积单位比面积单位大。 ×
(2)周长相等的两个圆,它们的面积也一定相等。 √
(3)正方体、长方体和圆柱体的体积都等于底面积乘高。 √
(4)圆柱体的侧面展开不一定是长方形。 √
(5)圆柱的体积比与它等底等高的圆锥的体积大。 ×
(6)一个正方体和一个圆锥体的底面积和高都相等,这个正方体的体积是圆锥体积的3倍。 √
【解答】解:由分析得:
(1)体积单位和面积单位是表示两个不同性质的量,无法比较大小,故原题说法错误;
(2)周长相等的两个圆,它们的面积也一定相等,故原题说法正确;
(3)正方体、长方体和圆柱体的体积都等于底面积乘高,故原题说法正确;
(4)圆柱体的侧面展开不一定是长方形,故原题说法正确;
(5)圆柱的体积比与它等底等高的圆锥的体积大2倍,故原题说法错误;
(6)一个正方体和一个圆锥体的底面积和高都相等,这个正方体的体积是圆锥体积的3倍,故原题说法正确。
故答案为:×;√;√;√;×;√。
14.圆柱的高是6厘米,和它体积相等,底面半径相等的圆锥的高是18厘米. √ .
【解答】解:底面半径相等,则这个圆柱与圆锥的底面积就相等,
设圆柱和圆锥的底面积相等是S,体积相等是V,所以它们的高的比是::=1:3,
因为圆柱的高是6厘米,
所以圆锥的高是:6×3=18(厘米),
答:圆锥的高是18厘米.
故答案为:√.
四.计算题(共2小题)
15.计算下面各圆锥的体积.
【解答】解:(1)3.14×62×12
=3.14×36×12
=452.16(立方厘米)
答:这个圆锥的体积是452.16立方厘米.
(2)3.14×(4÷2)2×7
=3.14×4×7
=(立方厘米)
答:这个圆锥的体积是立方厘米.
16.计算如图图形的表面积或体积。
(1)求表面积。(单位:cm)
(2)求体积。(单位:cm)
【解答】解:(1)3.14×4×20+3.14×(4÷2)2×2
=251.2+25.12
=276.32(cm)2
答:圆柱表面积为276.32cm2。
(2)×3.14×(6÷2)2×4+3.14×(6÷2)2×10
=3.14×3×4+3.14×9×10
=37.68+282.6
=320.28(cm)3
答:图形的体积为230.28cm3。
五.应用题(共4小题)
17.一个圆柱形水杯的容积是3.6升,底面积是1.2平方分米,装了杯水,水面离杯口高多少分米?
【解答】解:3.6÷1.2×(1﹣)
=3×
=0.75(分米)
答:水面离杯口高0.75分米.
18.把一个底面周长是31.4分米,高9分米的圆柱体铁块熔铸成一个底面半径是6分米的圆锥体,圆锥的高是多少分米?
【解答】解:3.14×(31.4÷3.14÷2)2×9×3÷(3.14×62)
=3.14×25×9×3÷113.04
=706.5×3÷113.04
=18.75(分米);
答:这个圆锥的高是18.7(5分)米.
19.一个圆柱,如果高减少2厘米,表面积就减少25.12平方厘米,体积减少.这个圆柱原来的体积是多少立方厘米?
【解答】解:圆柱的底面半径为:25.12÷2÷3.14÷2=2(厘米)
减少部分的体积为:3.14×22×2=25.12(立方厘米)
原来圆柱的体积为:25.12÷=125.6(立方厘米)
答:这个圆柱原来的体积为125.6立方厘米.
20.一个无盖的圆柱形铁皮水桶,高50厘米,底面直径40厘米,做这个水桶至少需要多少平方厘米的铁皮?
【解答】解:3.14×(40÷2)2+3.14×40×50
=1256+6280
=7536(平方厘米)
答:做这个水桶至少需要7536平方厘米的铁皮。
六.解答题(共2小题)
21.一个圆锥形沙堆,底面直径是8米,高是1.8米.它的体积大约是多少立方米?
【解答】解:圆锥的体积=×底面积×高
=×3.14×(8÷2)2×1.8,
=3.14×16×0.6,
=30.144(立方米);
答:这个圆锥形沙堆的体积是30.144立方米.
22.用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:厘米),打结处正好是底面圆心,打结用去绳长25厘米.扎这个盒子至少用去塑料绳多少厘米?在它的整个侧面贴上商标和说明,这部分的面积是多少平方厘米?
【解答】解:(1)15×8+50×8+25,
=120+400+25,
=545(厘米),
面积:3.14×50×15,
=157×15,
=2355(平方厘米);
答:扎这个盒子至少用去塑料绳545厘米,在它的整个侧面贴上商标和说明,这部分的面积是2355平方厘米.
一.选择题(共5小题)
1.右图中,瓶底的面积和锥形杯口的面积相等,将瓶子中的液体倒入锥形杯子、能倒满( )杯。
A.2 B.3 C.4 D.6
2.一个圆柱侧面展开是正方形,这个圆柱的底面半径是1分米,高是( )分米。
A.1 B.2 C.6.28
3.下面各图形以虚线为轴旋转一周形成几何体,( )图形成的体积与如图形成的体积相等。
A. B.
C. D.
4.把一块圆柱形铁块熔铸成与它等高的圆锥,底面积将( )
A.扩大到原来的3倍 B.缩小到原来的
C.与原来一样
5.一个高5cm,半径2cm的圆柱木料,将它锯成完全相同的两部分后,表面积可能增加了( )cm2。
A.20 B.40 C.12.56
二.填空题(共5小题)
6.把长2米的圆柱体原木切成大小一样的3个小圆柱之后,表面积增加了12.56cm2,这个圆柱体木头原来的表面积是 cm2,体积是 dm3。
7.如图是一个由圆柱和圆锥组成的陀螺,圆柱和圆锥的底面积相等,圆锥的高是圆柱高的。圆柱的体积是180立方厘米,陀螺的体积是 立方厘米。
8.一根长1米,横截面直径是20厘米的木头浮在水面上,小明发现它正好是一半露出水面,请你求出这根木头与水接触的面的面积是 平方厘米.
9.算一算,填一填。
名称 底面半径/cm 底面直径/cm 高/cm 表面积/cm2 体积/cm3
圆柱 10 4
4 10
圆锥 2 0.9 ﹣
30 5 ﹣
10.如图,圆锥形容器中装有2升水,水面高度正好是圆锥高度的一半,这个容器最多还可以装 升水。
三.判断题(共4小题)
11.一个圆锥的底面积增加20%,高减少20%,那么体积就不会改变。
12.一个圆柱的底面直径和高与正方体的棱长相等,那么它们的体积也相等. .
13.判断题。
(1)体积单位比面积单位大。
(2)周长相等的两个圆,它们的面积也一定相等。
(3)正方体、长方体和圆柱体的体积都等于底面积乘高。
(4)圆柱体的侧面展开不一定是长方形。
(5)圆柱的体积比与它等底等高的圆锥的体积大。
(6)一个正方体和一个圆锥体的底面积和高都相等,这个正方体的体积是圆锥体积的3倍。
14.圆柱的高是6厘米,和它体积相等,底面半径相等的圆锥的高是18厘米. .
四.计算题(共2小题)
15.计算下面各圆锥的体积.
16.计算如图图形的表面积或体积。
(1)求表面积。(单位:cm)
(2)求体积。(单位:cm)
五.应用题(共4小题)
17.一个圆柱形水杯的容积是3.6升,底面积是1.2平方分米,装了杯水,水面离杯口高多少分米?
18.把一个底面周长是31.4分米,高9分米的圆柱体铁块熔铸成一个底面半径是6分米的圆锥体,圆锥的高是多少分米?
19.一个圆柱,如果高减少2厘米,表面积就减少25.12平方厘米,体积减少.这个圆柱原来的体积是多少立方厘米?
20.一个无盖的圆柱形铁皮水桶,高50厘米,底面直径40厘米,做这个水桶至少需要多少平方厘米的铁皮?
21.一个圆锥形沙堆,底面直径是8米,高是1.8米.它的体积大约是多少立方米?
22.用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:厘米),打结处正好是底面圆心,打结用去绳长25厘米.扎这个盒子至少用去塑料绳多少厘米?在它的整个侧面贴上商标和说明,这部分的面积是多少平方厘米?
(培优篇) 2023-2024学年下学期小学数学人教新版六年级第3章练习卷
参考答案与试题解析
一.选择题(共5小题)
1.右图中,瓶底的面积和锥形杯口的面积相等,将瓶子中的液体倒入锥形杯子、能倒满( )杯。
A.2 B.3 C.4 D.6
【解答】解:3×2=6
答:能装满6杯。
故选:D。
2.一个圆柱侧面展开是正方形,这个圆柱的底面半径是1分米,高是( )分米。
A.1 B.2 C.6.28
【解答】解:2×3.14×1=6.28(分米)
答:高是6.28分米。
故选:C。
3.下面各图形以虚线为轴旋转一周形成几何体,( )图形成的体积与如图形成的体积相等。
A. B.
C. D.
【解答】解:π×22×6×=8π(cm3)
A、π×22×2=8π(cm3)
B、π×22×3=12π(cm3)
C、π×32×2=18π(cm3)
D、×π×62×2=24π(cm3)
故选:A。
4.把一块圆柱形铁块熔铸成与它等高的圆锥,底面积将( )
A.扩大到原来的3倍 B.缩小到原来的
C.与原来一样
【解答】解:把一块圆柱形铁块熔铸成与它等高的圆锥,底面积将扩大到原来的3倍。
故选:A。
5.一个高5cm,半径2cm的圆柱木料,将它锯成完全相同的两部分后,表面积可能增加了( )cm2。
A.20 B.40 C.12.56
【解答】解:5×2×2×2
=5×8
=40(平方厘米)
答:表面积可能增加了40cm2。
故选:B。
二.填空题(共5小题)
6.把长2米的圆柱体原木切成大小一样的3个小圆柱之后,表面积增加了12.56cm2,这个圆柱体木头原来的表面积是 1262.28 cm2,体积是 628 dm3。
【解答】解:12.56÷4=3.14(平方厘米)
3.14÷3.14=1(厘米)
2米=200厘米
3.14×2+3.14×1×2×200
=6.28+1256
=1262.28(平方厘米)
3.14×200=628(立方厘米)
答:这个圆柱体木头原来的表面积是1262.28cm2,体积是628dm3。
故答案为:1262.28,628。
7.如图是一个由圆柱和圆锥组成的陀螺,圆柱和圆锥的底面积相等,圆锥的高是圆柱高的。圆柱的体积是180立方厘米,陀螺的体积是 210 立方厘米。
【解答】解:180××
=60×
=30(立方厘米)
180+30=210(立方厘米)
答:陀螺的体积是210立方厘米。
故答案为:210。
8.一根长1米,横截面直径是20厘米的木头浮在水面上,小明发现它正好是一半露出水面,请你求出这根木头与水接触的面的面积是 3454 平方厘米.
【解答】解:木头横截面的半径为:20÷2=10(厘米),
两个底面积:3.14×102×2=628(平方厘米),
侧面积:3.14×20×100
=62.8×100,
=6280(平方厘米),
表面积:628+6280=6908(平方厘米),
与水接触的面积:6908÷2=3454(平方厘米)
答:这根木头与水接触的面的面积是3454平方厘米.
故答案为:3454.
9.算一算,填一填。
名称 底面半径/cm 底面直径/cm 高/cm 表面积/cm2 体积/cm3
圆柱 10 20 4 879.2 1256
2 4 10 150.72 125.6
圆锥 2 4 0.9 ﹣ 3.768
15 30 5 ﹣ 1177.5
【解答】解:10×2=20(厘米)
2×3.14×10×4+3.14×102×2
=62.8×4+3.14×100×2
=251.2+628
=879.2(平方厘米)
3.14×102×4
=3.14×100×4
=314×4
=1256(立方厘米)
4÷2=2(厘米)
3.14×4×10+3.14×22×2
=12.56×10+3.14×4×2
=125.6+25.12
=150.72(立方厘米)
3.14×22×10
=3.14×4×10
=125.6(立方厘米)
2×2=4(厘米)
×3.14×22×0.9
=×3.14×4×0.9
=3.768(立方厘米)
30÷2=15(厘米)
×3.14×152×5
=3.14×225×5
=1177.5(立方厘米)
填表如下:
名称 底面半径/cm 底面直径/cm 高/cm 表面积/cm2 体积/cm3
圆柱 10 20 4 879.2 1256
2 4 10 150.72 125.6
圆锥 2 4 0.9 ﹣ 3.768
15 30 5 ﹣ 1177.5
故答案为:20、879.2、1256;2、150.72、125.6;4、3.768;15、1177.5。
10.如图,圆锥形容器中装有2升水,水面高度正好是圆锥高度的一半,这个容器最多还可以装 14 升水。
【解答】解:如图:
可设容器中水的底面积为S1,圆锥形容器的底面积为S。
S1:S=()2:h2=1:4,即S=4S1
水的体积:
2=S1×=12
容器的容积:
Sh=×4S1
=×4×12
=16(升)
16﹣2=14(升)
答:这个容器还能装14升水。
故答案为:14。
三.判断题(共4小题)
11.一个圆锥的底面积增加20%,高减少20%,那么体积就不会改变。 ×
【解答】解:设原来圆锥的底面积为S,高为h,
原来的体积是:V=Sh
锥的底面积增加20%,高减少20%,
则变化后圆锥的体积为:V=×1.2S×0.8h
=0.32Sh
0.32Sh≠Sh
因此,一个圆锥的底面积增加20%,高减少20%,那么体积就不会改变。这种说法是错误的。
故答案为:×。
12.一个圆柱的底面直径和高与正方体的棱长相等,那么它们的体积也相等. × .
【解答】解:由圆柱和正方体的体积公式可知,一个圆柱和一个正方体的底面积和高相等,那么它们的体积也相等;
但这里圆柱的底面积与正方体的底面积不一定相等.
故答案为:×.
13.判断题。
(1)体积单位比面积单位大。 ×
(2)周长相等的两个圆,它们的面积也一定相等。 √
(3)正方体、长方体和圆柱体的体积都等于底面积乘高。 √
(4)圆柱体的侧面展开不一定是长方形。 √
(5)圆柱的体积比与它等底等高的圆锥的体积大。 ×
(6)一个正方体和一个圆锥体的底面积和高都相等,这个正方体的体积是圆锥体积的3倍。 √
【解答】解:由分析得:
(1)体积单位和面积单位是表示两个不同性质的量,无法比较大小,故原题说法错误;
(2)周长相等的两个圆,它们的面积也一定相等,故原题说法正确;
(3)正方体、长方体和圆柱体的体积都等于底面积乘高,故原题说法正确;
(4)圆柱体的侧面展开不一定是长方形,故原题说法正确;
(5)圆柱的体积比与它等底等高的圆锥的体积大2倍,故原题说法错误;
(6)一个正方体和一个圆锥体的底面积和高都相等,这个正方体的体积是圆锥体积的3倍,故原题说法正确。
故答案为:×;√;√;√;×;√。
14.圆柱的高是6厘米,和它体积相等,底面半径相等的圆锥的高是18厘米. √ .
【解答】解:底面半径相等,则这个圆柱与圆锥的底面积就相等,
设圆柱和圆锥的底面积相等是S,体积相等是V,所以它们的高的比是::=1:3,
因为圆柱的高是6厘米,
所以圆锥的高是:6×3=18(厘米),
答:圆锥的高是18厘米.
故答案为:√.
四.计算题(共2小题)
15.计算下面各圆锥的体积.
【解答】解:(1)3.14×62×12
=3.14×36×12
=452.16(立方厘米)
答:这个圆锥的体积是452.16立方厘米.
(2)3.14×(4÷2)2×7
=3.14×4×7
=(立方厘米)
答:这个圆锥的体积是立方厘米.
16.计算如图图形的表面积或体积。
(1)求表面积。(单位:cm)
(2)求体积。(单位:cm)
【解答】解:(1)3.14×4×20+3.14×(4÷2)2×2
=251.2+25.12
=276.32(cm)2
答:圆柱表面积为276.32cm2。
(2)×3.14×(6÷2)2×4+3.14×(6÷2)2×10
=3.14×3×4+3.14×9×10
=37.68+282.6
=320.28(cm)3
答:图形的体积为230.28cm3。
五.应用题(共4小题)
17.一个圆柱形水杯的容积是3.6升,底面积是1.2平方分米,装了杯水,水面离杯口高多少分米?
【解答】解:3.6÷1.2×(1﹣)
=3×
=0.75(分米)
答:水面离杯口高0.75分米.
18.把一个底面周长是31.4分米,高9分米的圆柱体铁块熔铸成一个底面半径是6分米的圆锥体,圆锥的高是多少分米?
【解答】解:3.14×(31.4÷3.14÷2)2×9×3÷(3.14×62)
=3.14×25×9×3÷113.04
=706.5×3÷113.04
=18.75(分米);
答:这个圆锥的高是18.7(5分)米.
19.一个圆柱,如果高减少2厘米,表面积就减少25.12平方厘米,体积减少.这个圆柱原来的体积是多少立方厘米?
【解答】解:圆柱的底面半径为:25.12÷2÷3.14÷2=2(厘米)
减少部分的体积为:3.14×22×2=25.12(立方厘米)
原来圆柱的体积为:25.12÷=125.6(立方厘米)
答:这个圆柱原来的体积为125.6立方厘米.
20.一个无盖的圆柱形铁皮水桶,高50厘米,底面直径40厘米,做这个水桶至少需要多少平方厘米的铁皮?
【解答】解:3.14×(40÷2)2+3.14×40×50
=1256+6280
=7536(平方厘米)
答:做这个水桶至少需要7536平方厘米的铁皮。
六.解答题(共2小题)
21.一个圆锥形沙堆,底面直径是8米,高是1.8米.它的体积大约是多少立方米?
【解答】解:圆锥的体积=×底面积×高
=×3.14×(8÷2)2×1.8,
=3.14×16×0.6,
=30.144(立方米);
答:这个圆锥形沙堆的体积是30.144立方米.
22.用塑料绳捆扎一个圆柱形的蛋糕盒(如图,单位:厘米),打结处正好是底面圆心,打结用去绳长25厘米.扎这个盒子至少用去塑料绳多少厘米?在它的整个侧面贴上商标和说明,这部分的面积是多少平方厘米?
【解答】解:(1)15×8+50×8+25,
=120+400+25,
=545(厘米),
面积:3.14×50×15,
=157×15,
=2355(平方厘米);
答:扎这个盒子至少用去塑料绳545厘米,在它的整个侧面贴上商标和说明,这部分的面积是2355平方厘米.
