第4章练习卷培优篇(单元测试)小学数学五年级下册 人教版 (含答案)
文档属性
| 名称 | 第4章练习卷培优篇(单元测试)小学数学五年级下册 人教版 (含答案) |  | |
| 格式 | Doc | ||
| 文件大小 | 214.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 20:37:30 | ||
图片预览




文档简介
(培优篇) 2023-2024学年下学期小学数学人教新版五年级第4章练习卷
一.选择题(共5小题)
1.如果a=4b(a、b都是非零自然数),那么a和b的最小公倍数是( )
A.a B.b C.ab D.4
2.一堆石子,用去它的后,又运来吨,现在的石子的质与原来的相比,( )
A.现在多 B.一样多 C.无法确定
3.通分后不能得到的分数是( )
A. B. C. D.
4.两根长3米的绳子,第一根用去,第二根用去米,剩下的绳子比较( )
A.第一根长 B.第二根长 C.一样长 D.无法比较
5.,(a和b为非0的数)那么a( )b。
A.大于 B.小于 C.等于 D.无法确定
二.填空题(共5小题)
6.如果a×=b×=c÷,(a、b、c均不为0),则a、b、c从小到大排列是 。
7.比较大小.
把1、1、1.85、1按从大到小的顺序排列. .
8.一个最简分数,分子、分母的和是86,如果分子、分母都减去9,得到的分数是,则原分数是 .
9.一个分数,若加上它的一个分数单位约分后是,若减去它的一个分数单位约分后是,这个分数原来是 。
10.米可以是 米的 分之 ;也可以是 米的 分之 .
三.判断题(共5小题)
11.如果小明体重的和小红体重的相等,那么小明比小红重。
12.两个自然数的乘积一定是它们的公倍数.
13.六(1)班和六(2)班的男生人数都占本班人数的,六(1)班和六(2)班的男生人数相等. .
14.大于而小于的最简分数只有一个. .
15.甲数的等于乙数的,乙数的等于丙数的(甲乙丙均不为零),则丙数最大。
四.计算题(共2小题)
16.下面各组的最大公因数和最小公倍数
13和52 14和49 12和16
13和91 16和42 8和24
7和15 16和24 18和12
17.求出下列各组数的最大公因数和最小公倍数。
(1)13和26 (2)10和15
五.应用题(共5小题)
18.五年级学生参加课外体育活动,其中20人参加长跑,15人参加排球,参加跳绳的人数比参加排球的少5人,参加跳绳人数的是参加排球人数的几分之几?
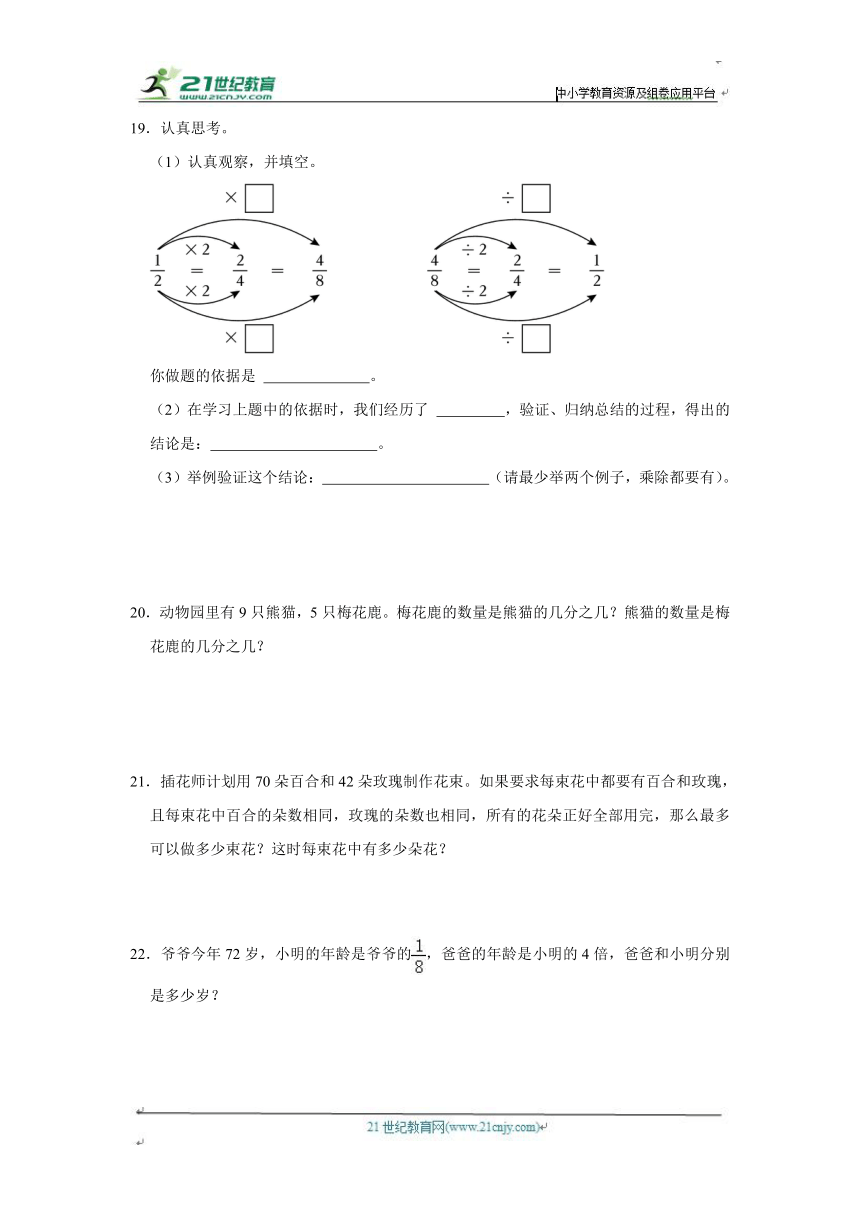
19.认真思考。
(1)认真观察,并填空。
你做题的依据是 。
(2)在学习上题中的依据时,我们经历了 ,验证、归纳总结的过程,得出的结论是: 。
(3)举例验证这个结论: (请最少举两个例子,乘除都要有)。
20.动物园里有9只熊猫,5只梅花鹿。梅花鹿的数量是熊猫的几分之几?熊猫的数量是梅花鹿的几分之几?
21.插花师计划用70朵百合和42朵玫瑰制作花束。如果要求每束花中都要有百合和玫瑰,且每束花中百合的朵数相同,玫瑰的朵数也相同,所有的花朵正好全部用完,那么最多可以做多少束花?这时每束花中有多少朵花?
22.爷爷今年72岁,小明的年龄是爷爷的,爸爸的年龄是小明的4倍,爸爸和小明分别是多少岁?
(培优篇) 2023-2024学年下学期小学数学人教新版五年级第4章练习卷
参考答案与试题解析
一.选择题(共5小题)
1.如果a=4b(a、b都是非零自然数),那么a和b的最小公倍数是( )
A.a B.b C.ab D.4
【解答】解:如果a=4b(a、b都是非零自然数),也就是a是b的倍数,所以a和b的最小公倍数是a。
故选:A。
2.一堆石子,用去它的后,又运来吨,现在的石子的质与原来的相比,( )
A.现在多 B.一样多 C.无法确定
【解答】解:堆石子,用去它的后,又运来吨,现在的石子的质与原来的相比,无法确定。
故选:C。
3.通分后不能得到的分数是( )
A. B. C. D.
【解答】解:==
==
==
答:通分后不能得到的分数是。
故选:B。
4.两根长3米的绳子,第一根用去,第二根用去米,剩下的绳子比较( )
A.第一根长 B.第二根长 C.一样长 D.无法比较
【解答】解:3×(1﹣)
=3×
=1.8(米)
3﹣=2.6(米)
2.6>1.8
因此第二根剩下的绳子长。
故选:B。
5.,(a和b为非0的数)那么a( )b。
A.大于 B.小于 C.等于 D.无法确定
【解答】解:依据题意可知:a×=b×
<,所以a>b。
故选:A。
二.填空题(共5小题)
6.如果a×=b×=c÷,(a、b、c均不为0),则a、b、c从小到大排列是 c<a<b 。
【解答】解:c÷=c×
a×=b×=c×
因为>,所以c<a<b
故答案为:c<a<b
7.比较大小.
把1、1、1.85、1按从大到小的顺序排列. 1>1>1.85>1 .
【解答】解:1=1.875、1=1.8、1=1.95
1.95>1.875>1.85>1.8
所以,1>1>1.85>1
故答案为:1>1>1.85>1.
8.一个最简分数,分子、分母的和是86,如果分子、分母都减去9,得到的分数是,则原分数是 .
【解答】解:新得到分数的分子分母的和是:
86﹣9×2=68;
原数的分母:
68×9÷(9+8)+9,
=612÷17+9,
=36+9,
=45;
原数的分子:
86﹣45=41;
原分数为:.
9.一个分数,若加上它的一个分数单位约分后是,若减去它的一个分数单位约分后是,这个分数原来是 。
【解答】解:(﹣)÷2=
﹣=
答:这个分数原来是。
故答案为:。
10.米可以是 1 米的 五 分之 四 ;也可以是 4 米的 五 分之 一 .
【解答】解:米可以是1米的五分之四;也可以是4米的五分一.
故答案为:1,五,四,4,五,一.
三.判断题(共5小题)
11.如果小明体重的和小红体重的相等,那么小明比小红重。 √
【解答】解:小明的体重:小红的体重=:=6:5,小明的体重6份大于小红的体重5份。
所以小明的体重更重些。所以原题说法正确。
故答案为:√。
12.两个自然数的乘积一定是它们的公倍数. ×
【解答】解:设这两个数为a、b,
如果a、b有一个为0,
则,ab不是a、b的公倍数.
所以“两个自然数的乘积一定是它们的公倍数”说法错误.
故答案为:×.
13.六(1)班和六(2)班的男生人数都占本班人数的,六(1)班和六(2)班的男生人数相等. × .
【解答】解:六(1)班和六(2)班的男生人数都占本班人数的,是把六(1)班的人数平均分成5份,男生占3份,把六(2)班学生人数平均分成5份,男生占3份,由六(1)班与六(2)班人数不一定相等,因此,六(1)班和六(2)班的男生人数不一定相等.原题的说法是错误的.
故答案为:×.
14.大于而小于的最简分数只有一个. × .
【解答】解:大于而小于的最简分数有、、…,所以原题是错误的.
故答案为:×.
15.甲数的等于乙数的,乙数的等于丙数的(甲乙丙均不为零),则丙数最大。 √
【解答】解:假设甲数×=乙数×=丙数×=1
甲数=5,乙数=6,丙数=7
丙数最大。所以原题说法正确。
故答案为:√。
四.计算题(共2小题)
16.下面各组的最大公因数和最小公倍数
13和52 14和49 12和16
13和91 16和42 8和24
7和15 16和24 18和12
【解答】解:13和52
52÷13=4
这两个数的最大公因数是13,最小公倍数是52;
14和49
14=2×7
49=7×7
这两个数的最大公因数是7,最小公倍数是2×7×7=98;
12和16
12=2×2×3
16=2×2×2×2
这两个数的最大公因数是2×2=4,最小公倍数是4×2×3×2=48;
13和91
91÷13=7
这两个数的最大公因数是13,最小公倍数是91.
16和42
16=2×2×2×2
42=2×3×7
这两个数的最大公因数是2,最小公倍数是2×2×2×2×3×7=336;
8和24
24÷8=3
这两个数的最大公因数是8,最小公倍数是24;
7和15
这两个数互质,最大公因数是1,最小公倍数是7×15=105;
16和24
16=2×2×2×2
24=2×2×2×3
这两个数的最大公因数是2×2×2=8,是小公倍数是8×2×3=48;
18和12
18=2×3×3
12=2×2×3
这两个数的最大公因数是2×3=6,最小公倍数是6×2×3=36.
17.求出下列各组数的最大公因数和最小公倍数。
(1)13和26 (2)10和15
【解答】解:(1)26是13的倍数,所以26和13的最大公因数是13,最小公倍数是26。
(2)10=2×5
15=3×5
所以10和15的最大公因数是5,最小公倍数是2×3×5=30;
五.应用题(共5小题)
18.五年级学生参加课外体育活动,其中20人参加长跑,15人参加排球,参加跳绳的人数比参加排球的少5人,参加跳绳人数的是参加排球人数的几分之几?
【解答】解:(15﹣5)÷15
=10÷15
=
答:参加跳绳人数的是参加排球人数的。
19.认真思考。
(1)认真观察,并填空。
你做题的依据是 分数的基本性质 。
(2)在学习上题中的依据时,我们经历了 猜想 ,验证、归纳总结的过程,得出的结论是: 分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质 。
(3)举例验证这个结论: =,=(答案不唯一) (请最少举两个例子,乘除都要有)。
【解答】解:(1)做题的依据是分数的基本性质。
(2)在学习上题中的依据时,我们经历了猜想,验证、归纳总结的过程,得出的结论是:分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质。
(3)举例验证这个结论:=,=。(答案不唯一)
故答案为:分数的基本性质,猜想,分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质,=,=。(答案不唯一)
20.动物园里有9只熊猫,5只梅花鹿。梅花鹿的数量是熊猫的几分之几?熊猫的数量是梅花鹿的几分之几?
【解答】解:5÷9=
9÷5=
答:梅花鹿的数量是熊猫的,熊猫的数量是梅花鹿的。
21.插花师计划用70朵百合和42朵玫瑰制作花束。如果要求每束花中都要有百合和玫瑰,且每束花中百合的朵数相同,玫瑰的朵数也相同,所有的花朵正好全部用完,那么最多可以做多少束花?这时每束花中有多少朵花?
【解答】解:70=2×5×7
42=2×3×7
所以70和42的最大公因数是2×7=14
70÷14=5(朵)
42÷14=3(朵)
5+3=8(朵)
答:最多可以做14束花,这时每束花中有8朵花。
22.爷爷今年72岁,小明的年龄是爷爷的,爸爸的年龄是小明的4倍,爸爸和小明分别是多少岁?
【解答】解:72÷8×1=9(岁)
9×4=36(岁)
答:爸爸今年36岁,小明今年9岁。
一.选择题(共5小题)
1.如果a=4b(a、b都是非零自然数),那么a和b的最小公倍数是( )
A.a B.b C.ab D.4
2.一堆石子,用去它的后,又运来吨,现在的石子的质与原来的相比,( )
A.现在多 B.一样多 C.无法确定
3.通分后不能得到的分数是( )
A. B. C. D.
4.两根长3米的绳子,第一根用去,第二根用去米,剩下的绳子比较( )
A.第一根长 B.第二根长 C.一样长 D.无法比较
5.,(a和b为非0的数)那么a( )b。
A.大于 B.小于 C.等于 D.无法确定
二.填空题(共5小题)
6.如果a×=b×=c÷,(a、b、c均不为0),则a、b、c从小到大排列是 。
7.比较大小.
把1、1、1.85、1按从大到小的顺序排列. .
8.一个最简分数,分子、分母的和是86,如果分子、分母都减去9,得到的分数是,则原分数是 .
9.一个分数,若加上它的一个分数单位约分后是,若减去它的一个分数单位约分后是,这个分数原来是 。
10.米可以是 米的 分之 ;也可以是 米的 分之 .
三.判断题(共5小题)
11.如果小明体重的和小红体重的相等,那么小明比小红重。
12.两个自然数的乘积一定是它们的公倍数.
13.六(1)班和六(2)班的男生人数都占本班人数的,六(1)班和六(2)班的男生人数相等. .
14.大于而小于的最简分数只有一个. .
15.甲数的等于乙数的,乙数的等于丙数的(甲乙丙均不为零),则丙数最大。
四.计算题(共2小题)
16.下面各组的最大公因数和最小公倍数
13和52 14和49 12和16
13和91 16和42 8和24
7和15 16和24 18和12
17.求出下列各组数的最大公因数和最小公倍数。
(1)13和26 (2)10和15
五.应用题(共5小题)
18.五年级学生参加课外体育活动,其中20人参加长跑,15人参加排球,参加跳绳的人数比参加排球的少5人,参加跳绳人数的是参加排球人数的几分之几?
19.认真思考。
(1)认真观察,并填空。
你做题的依据是 。
(2)在学习上题中的依据时,我们经历了 ,验证、归纳总结的过程,得出的结论是: 。
(3)举例验证这个结论: (请最少举两个例子,乘除都要有)。
20.动物园里有9只熊猫,5只梅花鹿。梅花鹿的数量是熊猫的几分之几?熊猫的数量是梅花鹿的几分之几?
21.插花师计划用70朵百合和42朵玫瑰制作花束。如果要求每束花中都要有百合和玫瑰,且每束花中百合的朵数相同,玫瑰的朵数也相同,所有的花朵正好全部用完,那么最多可以做多少束花?这时每束花中有多少朵花?
22.爷爷今年72岁,小明的年龄是爷爷的,爸爸的年龄是小明的4倍,爸爸和小明分别是多少岁?
(培优篇) 2023-2024学年下学期小学数学人教新版五年级第4章练习卷
参考答案与试题解析
一.选择题(共5小题)
1.如果a=4b(a、b都是非零自然数),那么a和b的最小公倍数是( )
A.a B.b C.ab D.4
【解答】解:如果a=4b(a、b都是非零自然数),也就是a是b的倍数,所以a和b的最小公倍数是a。
故选:A。
2.一堆石子,用去它的后,又运来吨,现在的石子的质与原来的相比,( )
A.现在多 B.一样多 C.无法确定
【解答】解:堆石子,用去它的后,又运来吨,现在的石子的质与原来的相比,无法确定。
故选:C。
3.通分后不能得到的分数是( )
A. B. C. D.
【解答】解:==
==
==
答:通分后不能得到的分数是。
故选:B。
4.两根长3米的绳子,第一根用去,第二根用去米,剩下的绳子比较( )
A.第一根长 B.第二根长 C.一样长 D.无法比较
【解答】解:3×(1﹣)
=3×
=1.8(米)
3﹣=2.6(米)
2.6>1.8
因此第二根剩下的绳子长。
故选:B。
5.,(a和b为非0的数)那么a( )b。
A.大于 B.小于 C.等于 D.无法确定
【解答】解:依据题意可知:a×=b×
<,所以a>b。
故选:A。
二.填空题(共5小题)
6.如果a×=b×=c÷,(a、b、c均不为0),则a、b、c从小到大排列是 c<a<b 。
【解答】解:c÷=c×
a×=b×=c×
因为>,所以c<a<b
故答案为:c<a<b
7.比较大小.
把1、1、1.85、1按从大到小的顺序排列. 1>1>1.85>1 .
【解答】解:1=1.875、1=1.8、1=1.95
1.95>1.875>1.85>1.8
所以,1>1>1.85>1
故答案为:1>1>1.85>1.
8.一个最简分数,分子、分母的和是86,如果分子、分母都减去9,得到的分数是,则原分数是 .
【解答】解:新得到分数的分子分母的和是:
86﹣9×2=68;
原数的分母:
68×9÷(9+8)+9,
=612÷17+9,
=36+9,
=45;
原数的分子:
86﹣45=41;
原分数为:.
9.一个分数,若加上它的一个分数单位约分后是,若减去它的一个分数单位约分后是,这个分数原来是 。
【解答】解:(﹣)÷2=
﹣=
答:这个分数原来是。
故答案为:。
10.米可以是 1 米的 五 分之 四 ;也可以是 4 米的 五 分之 一 .
【解答】解:米可以是1米的五分之四;也可以是4米的五分一.
故答案为:1,五,四,4,五,一.
三.判断题(共5小题)
11.如果小明体重的和小红体重的相等,那么小明比小红重。 √
【解答】解:小明的体重:小红的体重=:=6:5,小明的体重6份大于小红的体重5份。
所以小明的体重更重些。所以原题说法正确。
故答案为:√。
12.两个自然数的乘积一定是它们的公倍数. ×
【解答】解:设这两个数为a、b,
如果a、b有一个为0,
则,ab不是a、b的公倍数.
所以“两个自然数的乘积一定是它们的公倍数”说法错误.
故答案为:×.
13.六(1)班和六(2)班的男生人数都占本班人数的,六(1)班和六(2)班的男生人数相等. × .
【解答】解:六(1)班和六(2)班的男生人数都占本班人数的,是把六(1)班的人数平均分成5份,男生占3份,把六(2)班学生人数平均分成5份,男生占3份,由六(1)班与六(2)班人数不一定相等,因此,六(1)班和六(2)班的男生人数不一定相等.原题的说法是错误的.
故答案为:×.
14.大于而小于的最简分数只有一个. × .
【解答】解:大于而小于的最简分数有、、…,所以原题是错误的.
故答案为:×.
15.甲数的等于乙数的,乙数的等于丙数的(甲乙丙均不为零),则丙数最大。 √
【解答】解:假设甲数×=乙数×=丙数×=1
甲数=5,乙数=6,丙数=7
丙数最大。所以原题说法正确。
故答案为:√。
四.计算题(共2小题)
16.下面各组的最大公因数和最小公倍数
13和52 14和49 12和16
13和91 16和42 8和24
7和15 16和24 18和12
【解答】解:13和52
52÷13=4
这两个数的最大公因数是13,最小公倍数是52;
14和49
14=2×7
49=7×7
这两个数的最大公因数是7,最小公倍数是2×7×7=98;
12和16
12=2×2×3
16=2×2×2×2
这两个数的最大公因数是2×2=4,最小公倍数是4×2×3×2=48;
13和91
91÷13=7
这两个数的最大公因数是13,最小公倍数是91.
16和42
16=2×2×2×2
42=2×3×7
这两个数的最大公因数是2,最小公倍数是2×2×2×2×3×7=336;
8和24
24÷8=3
这两个数的最大公因数是8,最小公倍数是24;
7和15
这两个数互质,最大公因数是1,最小公倍数是7×15=105;
16和24
16=2×2×2×2
24=2×2×2×3
这两个数的最大公因数是2×2×2=8,是小公倍数是8×2×3=48;
18和12
18=2×3×3
12=2×2×3
这两个数的最大公因数是2×3=6,最小公倍数是6×2×3=36.
17.求出下列各组数的最大公因数和最小公倍数。
(1)13和26 (2)10和15
【解答】解:(1)26是13的倍数,所以26和13的最大公因数是13,最小公倍数是26。
(2)10=2×5
15=3×5
所以10和15的最大公因数是5,最小公倍数是2×3×5=30;
五.应用题(共5小题)
18.五年级学生参加课外体育活动,其中20人参加长跑,15人参加排球,参加跳绳的人数比参加排球的少5人,参加跳绳人数的是参加排球人数的几分之几?
【解答】解:(15﹣5)÷15
=10÷15
=
答:参加跳绳人数的是参加排球人数的。
19.认真思考。
(1)认真观察,并填空。
你做题的依据是 分数的基本性质 。
(2)在学习上题中的依据时,我们经历了 猜想 ,验证、归纳总结的过程,得出的结论是: 分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质 。
(3)举例验证这个结论: =,=(答案不唯一) (请最少举两个例子,乘除都要有)。
【解答】解:(1)做题的依据是分数的基本性质。
(2)在学习上题中的依据时,我们经历了猜想,验证、归纳总结的过程,得出的结论是:分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质。
(3)举例验证这个结论:=,=。(答案不唯一)
故答案为:分数的基本性质,猜想,分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质,=,=。(答案不唯一)
20.动物园里有9只熊猫,5只梅花鹿。梅花鹿的数量是熊猫的几分之几?熊猫的数量是梅花鹿的几分之几?
【解答】解:5÷9=
9÷5=
答:梅花鹿的数量是熊猫的,熊猫的数量是梅花鹿的。
21.插花师计划用70朵百合和42朵玫瑰制作花束。如果要求每束花中都要有百合和玫瑰,且每束花中百合的朵数相同,玫瑰的朵数也相同,所有的花朵正好全部用完,那么最多可以做多少束花?这时每束花中有多少朵花?
【解答】解:70=2×5×7
42=2×3×7
所以70和42的最大公因数是2×7=14
70÷14=5(朵)
42÷14=3(朵)
5+3=8(朵)
答:最多可以做14束花,这时每束花中有8朵花。
22.爷爷今年72岁,小明的年龄是爷爷的,爸爸的年龄是小明的4倍,爸爸和小明分别是多少岁?
【解答】解:72÷8×1=9(岁)
9×4=36(岁)
答:爸爸今年36岁,小明今年9岁。
