2022-2023学年福建省莆田市高二下学期期末质量监测数学试题(含解析)
文档属性
| 名称 | 2022-2023学年福建省莆田市高二下学期期末质量监测数学试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 00:00:00 | ||
图片预览




文档简介
2022-2023学年福建省莆田市高二下学期期末质量监测数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.从名男生,名女生中任选人,则选到名女生的概率为
( )
A. B. C. D.
2.函数的导函数是
( )
A. B. C. D.
3.若直线的方向向量为,平面的法向量为,则可能使的是
( )
A. , B. ,
C. , D. ,
4.甲每次投篮命中的概率为,且每次投篮相互独立,则在次连续投篮中甲命中的次数的方差是
( )
A. B. C. D.
5.若点平面,且对空间内任意一点满足,则的值是
( )
A. B. C. D.
6.如图,平行六面体的底面是矩形,其中,,,且,则线段的长为
( )
A. B. C. D.
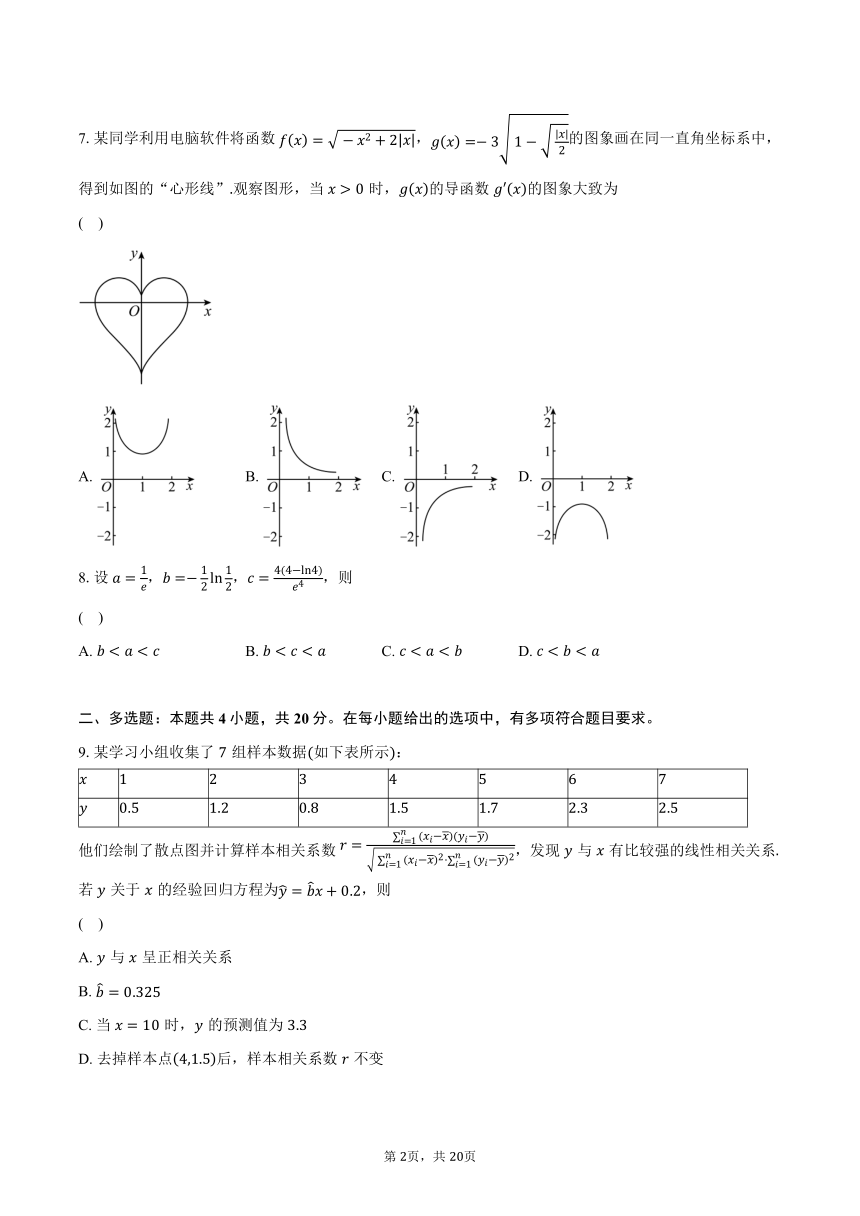
7.某同学利用电脑软件将函数,的图象画在同一直角坐标系中,得到如图的“心形线”观察图形,当时,的导函数的图象大致为
( )
A. B. C. D.
8.设,,,则
( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.某学习小组收集了组样本数据如下表所示:
他们绘制了散点图并计算样本相关系数,发现与有比较强的线性相关关系若关于的经验回归方程为,则
( )
A. 与呈正相关关系
B.
C. 当时,的预测值为
D. 去掉样本点后,样本相关系数不变
10.甲、乙两个罐子均装有个红球,个白球和个黑球,除颜色外,各个球完全相同先从甲罐中随机取出个球放入乙罐中,再从乙罐中随机取出个球,记事件表示从甲罐中取出的个球中含有个红球,表示从乙罐中取出的球是红球,则
( )
A. ,,两两互斥 B.
C. D. 与不相互独立
11.函数在处取得极大值,则
( )
A. B. 只有两个不同的零点
C. D. 在上的值域为
12.布达佩斯的伊帕姆维泽蒂博物馆收藏的达芬奇方砖是在正六边形上画了具有视觉效果的正方体图案如图把三片这样的达芬奇方砖拼成图的组合,这个组合再转换成图所示的几何体若图中每个正方体的棱长为,则
( )
A.
B. 若为线段上的一个动点,则的最大值为
C. 点到直线的距离是
D. 异面直线与所成角的正切值为
三、填空题:本题共4小题,每小题5分,共20分。
13.已知,,且,则 .
14.若某工厂制造的机械零件尺寸服从正态分布,则零件尺寸介于和之间的概率约为 .若,则,,
15.现从甲、乙、丙人中选派一人参加“垃圾分类”知识竞答,他们商议通过玩“石头、剪刀、布”游戏解决:如果其中两人手势相同,另一人不同,则选派手势不同的人参加;否则重新进行一局“石头、剪刀、布”游戏,直到确定人选为止在每局游戏中,甲、乙、丙各自出种手势是等可能的,且各局游戏是相互独立的,则直到第三局游戏才最终确定选派人员的概率为 .
16.已知函数,若直线是曲线的 切线,则 ;若直线与曲线交于,两点,且,则的取值范围是 .
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知函数.
当时,求的极值;
若在上单调递减,求的取值范围.
18.本小题分
如图,在边长为的正方体中,,分别为,的中点.
求点到平面的距离;
求二面角的大小.
19.本小题分
甲、乙两位好友进行乒乓球友谊赛,比赛采用局胜制,若每局比赛甲获胜的概率为,且每局比赛的结果是相互独立的.
比赛采用局胜制,在甲在第一局落败的条件下,求甲反败为胜的概率;
比赛采用局胜制,比赛结束时,求甲获胜的局数的分布列及数学期望.
20.本小题分
如图,在四棱锥中,,,,为的中点,与均为等边三角形,与相交于点
证明:平面;
求直线与平面所成的角的正弦值.
21.本小题分
为了考查一种新疫苗预防某一疾病的效果,研究人员对一地区某种动物进行试验,从该试验群中随机抽查了只,得到如下的样本数据单位:只:
发病 没发病 合计
接种疫苗
没接种疫苗
合计
能否有的把握认为接种该疫苗与预防该疾病有关?
从该地区此动物群中任取一只,记表示此动物发病,表示此动物没发病,表示此动物接种疫苗,定义事件的优势,在事件发生的条件下的优势.
(ⅰ)证明:;
(ⅱ)利用抽样的样本数据,给出,的估计值,并给出的估计值附:,其中.
22.本小题分
已知函数,其中.
讨论的单调性;
若有两个零点,,且,求的最小值.
答案和解析
1.【答案】
【解析】【分析】
本题考查古典概型及其计算,属于基础题.
首先为男生,女生编号,再结合样本空间,和古典概型概率公式,即可求解.
【解答】
解:设名男生的编号为 ,名女生的编号为 ,
任取人的样本空间包含 共个样本点,
其中选到名女生为 共个样本点,
所以选到名女生的概率 .
故选:.
2.【答案】
【解析】【分析】
本题考查基本初等函数的导数公式,
利用幂函数的导数公式,即可求解.
【解答】
解: .
故选:
3.【答案】
【解析】【分析】
本题考查线面平行时,方向向量与法向量的关系垂直,属于基础题.
根据线面的位置关系,可知 ,结合选项,即可判断.
【解答】
解:要使 ,则 ,
A. , , , .
故选:
4.【答案】
【解析】【分析】
本题考查二项分布,属于基础题.
根据题意,命中的次数随机变量 ,由二项分布方差公式求解.
【解答】
解:根据题意,命中的次数随机变量 ,
由二项分布方差公式得, .
故选:
5.【答案】
【解析】【分析】
本题考查向量表示四点共面具有的性质,属于一般题.
根据条件得出 , , , 四点共面,再根据 即可求出 的值.
【解答】
解: 平面 ,
, , , 四点共面,
又 ,
,解得 .
故选:.
6.【答案】
【解析】【分析】
本题考查空间向量数量积运算,属于中档题.
由 ,两边平方,利用勾股定理以及数量积的定义求出 的值,进而可得答案
【解答】
解:由 ,
.
因为底面 是矩形, , , ,
所以 , ,
因为 ,
所以 ,
所以 ,
,
故选:.
7.【答案】
【解析】【分析】
本题考查函数与其导函数的关系,属于基础题。
首先确定函数 的图象,再结合导数于函数图象间的关系,即可判断选项.
【解答】
解: , ,
所以 轴下方的图象为函数 的图象,
当 时,函数 单调递增,所以 ,故排除;
根据导数的几何意义可知, 时,函数 图象上每点处的切线斜率应先变小,再增大,故排除,只有A正确.
故选:
8.【答案】
【解析】【分析】
本题考查比较大小,解题的关键是对 变形,使形式相同,然后构造函数,判断函数的单调性,再利用单调性比较大小,考查数学转化思想和计算能力,属于难题.
由于 , , ,所以构造函数 ,然后利用导数判断函数的单调性,再利用函数单调性可比较大小。
【解答】
解: , , ,
令 ,则 ,
由 ,得 ,
当 时, ,当 时, ,
所以 在 上递增,在 上递减,
因为 ,所以 ,
所以 ,
故选:
9.【答案】
【解析】【分析】
本题考查回归方程的求解以及相应的性质,属于一般题.
首先求,根据样本中心求回归直线方程,即可判断选项.
【解答】
解:由数据可知,,,样本点中心必在回归直线上,
所以,得,故 AB正确;
,当时,,故 C错误;
因为是样本点中心,,所以去掉这一项,样本相关系数不变,故 D正确.
故选:
10.【答案】
【解析】【分析】
本题考查条件和全概率以及互斥,独立事件等定义,属于中档题.
结合互斥,相互独立事件的定义,以及全概率公式,条件概率公式,即可判断选项.
【解答】
解:.表示从甲罐中取出的个球,没有红球,表示从甲罐中取出的个球,有个红球,表示从甲罐中取出的个球,有个红球,在一次实验中,这三个事件,任两个事件不能同时发生,所以两两互斥,故A正确;
B.,故 B错误;
C.
,故 C正确;
D.,,,
则,则与相互独立,故 D错误.
故选:
11.【答案】
【解析】【分析】
本题考查利用导数求函数的最值不含参,利用导数根据极值或极值点求参,利用导数研究函数的零点或方程的根,
首先根据极值点求函数的解析式,再利用导数判断函数的单调性,结合函数的单调性,极值和端点值,即可判断选项.
【解答】
解:,,
由条件可知,,得,
当时,,得或,
单调递减 极小值 单调递增 单调递减
由表格数据单调性可知,单调递减,且,所以函数在区间有个零点,同理,函数在区间和也各有个零点,所以函数有个不同的零点,故A正确,B错误;
,,,,故 C正确;
,再结合表格数据可知,函数在区间上的值域为,故 D错误.
故选:
12.【答案】
【解析】【分析】
本题考查空间向量的线性运算、直线与直线所成角的向量求法、空间向量运算的坐标表示、点线距离的向量求法,属于较难题.
根据空间向量线性运算法则判断,以为坐标原点,所在直线为轴,所在直线为轴建立空间直角坐标系,利用空间向量法计算、、.
【解答】
解:因为,
所以,故 A错误;
如图,以为坐标原点,建立空间直角坐标系,
则,,,,,,,
所以,,,,,
对于:因为为线段上的一个动点,设,,
则,
所以,所以当时,,故 B正确;
对于:,所以,
所以点到直线的距离,故 C正确;
对于:因为,
所以,
所以,即异面直线与所成角的正切值为,故 D正确;
故选:
13.【答案】
【解析】【分析】
本题考查空间向量平行共线的坐标表示,
利用向量共线定理列方程求得 ,从而可得答案.
【解答】
解:因为 , ,且 ,
, ,
则 ,解得: ,
.
故答案为:
14.【答案】
【解析】【分析】
本题考查正态分布的概率,属于中档题.
由题意可得 ,然后代值计算即可.
【解答】
解:因为 服从正态分布 ,所以 ,
所以 ,
所以
,
故答案为:
15.【答案】
【解析】【分析】
本题考查组合与组合数公式、相互独立事件的概率乘法公式,属于中档题.
根据题意,先求出进行一局游戏,成功确定和没有确定参加活动人选的概率,然后根据各局游戏是相互独立,即可得到结果.
【解答】
解:设事件 表示“进行一局游戏,成功确定参加活动人选”,
则 ,
则进行一局游戏,没有确定参加活动人选的概率为 ,
且各局游戏是相互独立的,
则直到第三局游戏才最终确定选派人员的概率为 .
故答案为: .
16.【答案】
【解析】【分析】
本题考查了导数的综合运用,求某点处的切线方程较为简单,利用导数求单调性.
对函数 求导,设出切点,由导数的几何意义可得 ,由此可得 的值;依题意,直线 与曲线 有两个交点,利用导数研究函数 的性质,可知 则由 ,可令 ,进一步可得 ,设 ,则 ,利用导数求出 的范围,即可得到 的范围.
【解答】
解:记 , ,
设切线 与曲线 相切于点 , ,
则 ,解得 ,即实数 的值为 ;
令 ,则 ,依题意,直线 与曲线 有两个交点,
又 ,
令 ,解得 ,令 ,解得 ,
则函数 在 上单调递增,在 上单调递减,且 ,当 时, ,当 时, ,
作出函数 的大致图象如图所示,
由图象可知:要使直线 与曲线 有两个交点,则
又 ,则 ,则 ,
令 ,则 ,
又 ,则 ,
于是 ,则 ,故 ,
设 ,则 ,
又 ,设 ,
则 ,
故 在 , 上单调递减,则 ,
故 在 , 上恒成立,则 在 , 上单调递减,
于是 ,
又函数 在 上单调递增,则当 时, .
故答案为: ; .
17.【答案】解:当时,,
所以,得或,
当时,解得:或,当时,解得:,
所以函数的单调递增区间是和,单调递减区间是,
当变换时,,的变化情况如下表所示,
单调递增 极大值 单调递减 极小值 单调递增
所以函数的的极大值为,极小值为;
,,,
因为在上单调递减,
可得在上恒成立,
即在上恒成立,
当时,,
所以,即的取值范围是.
【解析】本题考查了利用导数研究函数的单调性与极值,考查了转化思想,属中档题.
首先求函数的导数,利用导数判断函数的单调性,即可求函数的极值;
利用导数,将不等式恒成立,转化为在上恒成立,即可求解.
18.【答案】解:如图,以点 为原点,建立空间直角坐标系,
, , , , ,
, ,
设平面 的 法向量为 ,
则 ,即 ,令 ,则 ,
所以平面 的法向量为 ,
所以点 到平面 的距离 ;
因为 ,
平面 , 平面 ,
所以 ,且 , 平面 ,
所以 平面 ,即 平面 ,
, , ,
,
所以二面角 的 大小为 .
【解析】本题考查向量形式下,点到直线的求解,以及利用垂直求二面角,属于综合题。
首先,建立空间直角坐标系,求平面 的法向量,利用点到平面的距离公式,即可求解;
利用垂直关系证明 平面 ,利用法向量求二面角的大小.
19.【答案】解:记 “甲在第一局落败”, “甲反败为胜”,
甲最终获胜有两种可能的比分 或 ,且每局比赛结果是相互独立的.
若比分是 ,则甲接下来连胜局,其概率为 ;
若比分是 ,则第,,局比赛中甲胜局输局且第局甲获胜,
其概率为 ,所以 .
的所有可能取值为 ,
,
,
,
所以 的分布列为
则 .
【解析】本题考查条件概率的概念与计算、离散型随机变量的均值和分布列,属于中档题.
根据题意,分别求出比分 或 的概率,即可得到结果;
由题意可知, 的所有可能取值为 ,然后分别求出其对应的概率,即可得到结果.
20.【答案】解:取 的中点 ,连接 , ,
因为 是等边三角形,所以 ,
因为 , , 为 的中点,
所以四边形 是正方形,所以 ,则 ,
且 , 平面 ,
所以 平面 , 平面 ,
所以 ,
又因为 与 均为等边三角形,所以 ,
所以 ,且 , 平面 ,
所以 平面
四边形 是正方形,所以 ,
以点 为原点,以 为 轴,建立空间直角坐标系,
, , ,
, , , ,
, ,
设平面 的法向量为 ,
则 ,即 ,得
令 ,所以平面 的法向量 ,
设直线 与平面 的夹角为 ,
所以 ,
所以直线 与平面 的夹角的正弦值 .
【解析】本题考查线面垂直的判定以及线面夹角的计算,属于中档题.
要证明线面垂直,可证明 垂直于平面内的两条相交直线,利用垂直关系,构造辅助线,即可证明;
根据的结果,建立空间直角坐标系,求平面 的法向量,利用向量夹角公式求线面角的正弦值.
21.【答案】解:根据联表可得 ,
所以有的把握认为接种该疫苗与预防该疾病有关.
由于 ,
所以 , ,
故 ,故得证.
(ⅱ)由二联表中的数据可得 , ,
所以 .
【解析】本题考查独立性检验,考查条件概率的概念与计算,属于较难题.
根据的计算即可与临界值比较求解,
根据条件概率的计算公式,即可结合 的定义进行求证,进而求解.
22.【答案】解: 定义域为 ,
且 ,
当 时, 恒成立,所以 在 上单调递减;
当 时,令 得 ,
当 时, ;当 时, ,
所以 在 上单调递减,在 上单调递增.
综上可得:当 时 在 上单调递减;
当 时 在 上单调递减,在 上单调递增.
因为 ,所以 ,
所以 , ,
所以 ,
所以 ,
令 ,因为 ,所以 ,即 ,
所以 , ,
令 , ,
则 ,
令 , ,
则 ,
所以 在 上单调递增,又 ,所以 ,
即 ,所以 在 上单调递减,
所以 ,
所以 ,即 ,即 ,
当且仅当 ,即 时等号成立,
所以 的最小值为 .
【解析】本题考查利用导函数判断函数的单调性以及利用函数零点等已知求解最值,属于综合题.
导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极最值问题处理.
求出函数的导函数,再分 、 两种情况讨论,分别求出函数的单调性;
依题意可得 ,即可得到 ,从而得到 ,令 , ,令 , ,利用导数求出 的最小值,即可求出 的最小值.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.从名男生,名女生中任选人,则选到名女生的概率为
( )
A. B. C. D.
2.函数的导函数是
( )
A. B. C. D.
3.若直线的方向向量为,平面的法向量为,则可能使的是
( )
A. , B. ,
C. , D. ,
4.甲每次投篮命中的概率为,且每次投篮相互独立,则在次连续投篮中甲命中的次数的方差是
( )
A. B. C. D.
5.若点平面,且对空间内任意一点满足,则的值是
( )
A. B. C. D.
6.如图,平行六面体的底面是矩形,其中,,,且,则线段的长为
( )
A. B. C. D.
7.某同学利用电脑软件将函数,的图象画在同一直角坐标系中,得到如图的“心形线”观察图形,当时,的导函数的图象大致为
( )
A. B. C. D.
8.设,,,则
( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.某学习小组收集了组样本数据如下表所示:
他们绘制了散点图并计算样本相关系数,发现与有比较强的线性相关关系若关于的经验回归方程为,则
( )
A. 与呈正相关关系
B.
C. 当时,的预测值为
D. 去掉样本点后,样本相关系数不变
10.甲、乙两个罐子均装有个红球,个白球和个黑球,除颜色外,各个球完全相同先从甲罐中随机取出个球放入乙罐中,再从乙罐中随机取出个球,记事件表示从甲罐中取出的个球中含有个红球,表示从乙罐中取出的球是红球,则
( )
A. ,,两两互斥 B.
C. D. 与不相互独立
11.函数在处取得极大值,则
( )
A. B. 只有两个不同的零点
C. D. 在上的值域为
12.布达佩斯的伊帕姆维泽蒂博物馆收藏的达芬奇方砖是在正六边形上画了具有视觉效果的正方体图案如图把三片这样的达芬奇方砖拼成图的组合,这个组合再转换成图所示的几何体若图中每个正方体的棱长为,则
( )
A.
B. 若为线段上的一个动点,则的最大值为
C. 点到直线的距离是
D. 异面直线与所成角的正切值为
三、填空题:本题共4小题,每小题5分,共20分。
13.已知,,且,则 .
14.若某工厂制造的机械零件尺寸服从正态分布,则零件尺寸介于和之间的概率约为 .若,则,,
15.现从甲、乙、丙人中选派一人参加“垃圾分类”知识竞答,他们商议通过玩“石头、剪刀、布”游戏解决:如果其中两人手势相同,另一人不同,则选派手势不同的人参加;否则重新进行一局“石头、剪刀、布”游戏,直到确定人选为止在每局游戏中,甲、乙、丙各自出种手势是等可能的,且各局游戏是相互独立的,则直到第三局游戏才最终确定选派人员的概率为 .
16.已知函数,若直线是曲线的 切线,则 ;若直线与曲线交于,两点,且,则的取值范围是 .
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知函数.
当时,求的极值;
若在上单调递减,求的取值范围.
18.本小题分
如图,在边长为的正方体中,,分别为,的中点.
求点到平面的距离;
求二面角的大小.
19.本小题分
甲、乙两位好友进行乒乓球友谊赛,比赛采用局胜制,若每局比赛甲获胜的概率为,且每局比赛的结果是相互独立的.
比赛采用局胜制,在甲在第一局落败的条件下,求甲反败为胜的概率;
比赛采用局胜制,比赛结束时,求甲获胜的局数的分布列及数学期望.
20.本小题分
如图,在四棱锥中,,,,为的中点,与均为等边三角形,与相交于点
证明:平面;
求直线与平面所成的角的正弦值.
21.本小题分
为了考查一种新疫苗预防某一疾病的效果,研究人员对一地区某种动物进行试验,从该试验群中随机抽查了只,得到如下的样本数据单位:只:
发病 没发病 合计
接种疫苗
没接种疫苗
合计
能否有的把握认为接种该疫苗与预防该疾病有关?
从该地区此动物群中任取一只,记表示此动物发病,表示此动物没发病,表示此动物接种疫苗,定义事件的优势,在事件发生的条件下的优势.
(ⅰ)证明:;
(ⅱ)利用抽样的样本数据,给出,的估计值,并给出的估计值附:,其中.
22.本小题分
已知函数,其中.
讨论的单调性;
若有两个零点,,且,求的最小值.
答案和解析
1.【答案】
【解析】【分析】
本题考查古典概型及其计算,属于基础题.
首先为男生,女生编号,再结合样本空间,和古典概型概率公式,即可求解.
【解答】
解:设名男生的编号为 ,名女生的编号为 ,
任取人的样本空间包含 共个样本点,
其中选到名女生为 共个样本点,
所以选到名女生的概率 .
故选:.
2.【答案】
【解析】【分析】
本题考查基本初等函数的导数公式,
利用幂函数的导数公式,即可求解.
【解答】
解: .
故选:
3.【答案】
【解析】【分析】
本题考查线面平行时,方向向量与法向量的关系垂直,属于基础题.
根据线面的位置关系,可知 ,结合选项,即可判断.
【解答】
解:要使 ,则 ,
A. , , , .
故选:
4.【答案】
【解析】【分析】
本题考查二项分布,属于基础题.
根据题意,命中的次数随机变量 ,由二项分布方差公式求解.
【解答】
解:根据题意,命中的次数随机变量 ,
由二项分布方差公式得, .
故选:
5.【答案】
【解析】【分析】
本题考查向量表示四点共面具有的性质,属于一般题.
根据条件得出 , , , 四点共面,再根据 即可求出 的值.
【解答】
解: 平面 ,
, , , 四点共面,
又 ,
,解得 .
故选:.
6.【答案】
【解析】【分析】
本题考查空间向量数量积运算,属于中档题.
由 ,两边平方,利用勾股定理以及数量积的定义求出 的值,进而可得答案
【解答】
解:由 ,
.
因为底面 是矩形, , , ,
所以 , ,
因为 ,
所以 ,
所以 ,
,
故选:.
7.【答案】
【解析】【分析】
本题考查函数与其导函数的关系,属于基础题。
首先确定函数 的图象,再结合导数于函数图象间的关系,即可判断选项.
【解答】
解: , ,
所以 轴下方的图象为函数 的图象,
当 时,函数 单调递增,所以 ,故排除;
根据导数的几何意义可知, 时,函数 图象上每点处的切线斜率应先变小,再增大,故排除,只有A正确.
故选:
8.【答案】
【解析】【分析】
本题考查比较大小,解题的关键是对 变形,使形式相同,然后构造函数,判断函数的单调性,再利用单调性比较大小,考查数学转化思想和计算能力,属于难题.
由于 , , ,所以构造函数 ,然后利用导数判断函数的单调性,再利用函数单调性可比较大小。
【解答】
解: , , ,
令 ,则 ,
由 ,得 ,
当 时, ,当 时, ,
所以 在 上递增,在 上递减,
因为 ,所以 ,
所以 ,
故选:
9.【答案】
【解析】【分析】
本题考查回归方程的求解以及相应的性质,属于一般题.
首先求,根据样本中心求回归直线方程,即可判断选项.
【解答】
解:由数据可知,,,样本点中心必在回归直线上,
所以,得,故 AB正确;
,当时,,故 C错误;
因为是样本点中心,,所以去掉这一项,样本相关系数不变,故 D正确.
故选:
10.【答案】
【解析】【分析】
本题考查条件和全概率以及互斥,独立事件等定义,属于中档题.
结合互斥,相互独立事件的定义,以及全概率公式,条件概率公式,即可判断选项.
【解答】
解:.表示从甲罐中取出的个球,没有红球,表示从甲罐中取出的个球,有个红球,表示从甲罐中取出的个球,有个红球,在一次实验中,这三个事件,任两个事件不能同时发生,所以两两互斥,故A正确;
B.,故 B错误;
C.
,故 C正确;
D.,,,
则,则与相互独立,故 D错误.
故选:
11.【答案】
【解析】【分析】
本题考查利用导数求函数的最值不含参,利用导数根据极值或极值点求参,利用导数研究函数的零点或方程的根,
首先根据极值点求函数的解析式,再利用导数判断函数的单调性,结合函数的单调性,极值和端点值,即可判断选项.
【解答】
解:,,
由条件可知,,得,
当时,,得或,
单调递减 极小值 单调递增 单调递减
由表格数据单调性可知,单调递减,且,所以函数在区间有个零点,同理,函数在区间和也各有个零点,所以函数有个不同的零点,故A正确,B错误;
,,,,故 C正确;
,再结合表格数据可知,函数在区间上的值域为,故 D错误.
故选:
12.【答案】
【解析】【分析】
本题考查空间向量的线性运算、直线与直线所成角的向量求法、空间向量运算的坐标表示、点线距离的向量求法,属于较难题.
根据空间向量线性运算法则判断,以为坐标原点,所在直线为轴,所在直线为轴建立空间直角坐标系,利用空间向量法计算、、.
【解答】
解:因为,
所以,故 A错误;
如图,以为坐标原点,建立空间直角坐标系,
则,,,,,,,
所以,,,,,
对于:因为为线段上的一个动点,设,,
则,
所以,所以当时,,故 B正确;
对于:,所以,
所以点到直线的距离,故 C正确;
对于:因为,
所以,
所以,即异面直线与所成角的正切值为,故 D正确;
故选:
13.【答案】
【解析】【分析】
本题考查空间向量平行共线的坐标表示,
利用向量共线定理列方程求得 ,从而可得答案.
【解答】
解:因为 , ,且 ,
, ,
则 ,解得: ,
.
故答案为:
14.【答案】
【解析】【分析】
本题考查正态分布的概率,属于中档题.
由题意可得 ,然后代值计算即可.
【解答】
解:因为 服从正态分布 ,所以 ,
所以 ,
所以
,
故答案为:
15.【答案】
【解析】【分析】
本题考查组合与组合数公式、相互独立事件的概率乘法公式,属于中档题.
根据题意,先求出进行一局游戏,成功确定和没有确定参加活动人选的概率,然后根据各局游戏是相互独立,即可得到结果.
【解答】
解:设事件 表示“进行一局游戏,成功确定参加活动人选”,
则 ,
则进行一局游戏,没有确定参加活动人选的概率为 ,
且各局游戏是相互独立的,
则直到第三局游戏才最终确定选派人员的概率为 .
故答案为: .
16.【答案】
【解析】【分析】
本题考查了导数的综合运用,求某点处的切线方程较为简单,利用导数求单调性.
对函数 求导,设出切点,由导数的几何意义可得 ,由此可得 的值;依题意,直线 与曲线 有两个交点,利用导数研究函数 的性质,可知 则由 ,可令 ,进一步可得 ,设 ,则 ,利用导数求出 的范围,即可得到 的范围.
【解答】
解:记 , ,
设切线 与曲线 相切于点 , ,
则 ,解得 ,即实数 的值为 ;
令 ,则 ,依题意,直线 与曲线 有两个交点,
又 ,
令 ,解得 ,令 ,解得 ,
则函数 在 上单调递增,在 上单调递减,且 ,当 时, ,当 时, ,
作出函数 的大致图象如图所示,
由图象可知:要使直线 与曲线 有两个交点,则
又 ,则 ,则 ,
令 ,则 ,
又 ,则 ,
于是 ,则 ,故 ,
设 ,则 ,
又 ,设 ,
则 ,
故 在 , 上单调递减,则 ,
故 在 , 上恒成立,则 在 , 上单调递减,
于是 ,
又函数 在 上单调递增,则当 时, .
故答案为: ; .
17.【答案】解:当时,,
所以,得或,
当时,解得:或,当时,解得:,
所以函数的单调递增区间是和,单调递减区间是,
当变换时,,的变化情况如下表所示,
单调递增 极大值 单调递减 极小值 单调递增
所以函数的的极大值为,极小值为;
,,,
因为在上单调递减,
可得在上恒成立,
即在上恒成立,
当时,,
所以,即的取值范围是.
【解析】本题考查了利用导数研究函数的单调性与极值,考查了转化思想,属中档题.
首先求函数的导数,利用导数判断函数的单调性,即可求函数的极值;
利用导数,将不等式恒成立,转化为在上恒成立,即可求解.
18.【答案】解:如图,以点 为原点,建立空间直角坐标系,
, , , , ,
, ,
设平面 的 法向量为 ,
则 ,即 ,令 ,则 ,
所以平面 的法向量为 ,
所以点 到平面 的距离 ;
因为 ,
平面 , 平面 ,
所以 ,且 , 平面 ,
所以 平面 ,即 平面 ,
, , ,
,
所以二面角 的 大小为 .
【解析】本题考查向量形式下,点到直线的求解,以及利用垂直求二面角,属于综合题。
首先,建立空间直角坐标系,求平面 的法向量,利用点到平面的距离公式,即可求解;
利用垂直关系证明 平面 ,利用法向量求二面角的大小.
19.【答案】解:记 “甲在第一局落败”, “甲反败为胜”,
甲最终获胜有两种可能的比分 或 ,且每局比赛结果是相互独立的.
若比分是 ,则甲接下来连胜局,其概率为 ;
若比分是 ,则第,,局比赛中甲胜局输局且第局甲获胜,
其概率为 ,所以 .
的所有可能取值为 ,
,
,
,
所以 的分布列为
则 .
【解析】本题考查条件概率的概念与计算、离散型随机变量的均值和分布列,属于中档题.
根据题意,分别求出比分 或 的概率,即可得到结果;
由题意可知, 的所有可能取值为 ,然后分别求出其对应的概率,即可得到结果.
20.【答案】解:取 的中点 ,连接 , ,
因为 是等边三角形,所以 ,
因为 , , 为 的中点,
所以四边形 是正方形,所以 ,则 ,
且 , 平面 ,
所以 平面 , 平面 ,
所以 ,
又因为 与 均为等边三角形,所以 ,
所以 ,且 , 平面 ,
所以 平面
四边形 是正方形,所以 ,
以点 为原点,以 为 轴,建立空间直角坐标系,
, , ,
, , , ,
, ,
设平面 的法向量为 ,
则 ,即 ,得
令 ,所以平面 的法向量 ,
设直线 与平面 的夹角为 ,
所以 ,
所以直线 与平面 的夹角的正弦值 .
【解析】本题考查线面垂直的判定以及线面夹角的计算,属于中档题.
要证明线面垂直,可证明 垂直于平面内的两条相交直线,利用垂直关系,构造辅助线,即可证明;
根据的结果,建立空间直角坐标系,求平面 的法向量,利用向量夹角公式求线面角的正弦值.
21.【答案】解:根据联表可得 ,
所以有的把握认为接种该疫苗与预防该疾病有关.
由于 ,
所以 , ,
故 ,故得证.
(ⅱ)由二联表中的数据可得 , ,
所以 .
【解析】本题考查独立性检验,考查条件概率的概念与计算,属于较难题.
根据的计算即可与临界值比较求解,
根据条件概率的计算公式,即可结合 的定义进行求证,进而求解.
22.【答案】解: 定义域为 ,
且 ,
当 时, 恒成立,所以 在 上单调递减;
当 时,令 得 ,
当 时, ;当 时, ,
所以 在 上单调递减,在 上单调递增.
综上可得:当 时 在 上单调递减;
当 时 在 上单调递减,在 上单调递增.
因为 ,所以 ,
所以 , ,
所以 ,
所以 ,
令 ,因为 ,所以 ,即 ,
所以 , ,
令 , ,
则 ,
令 , ,
则 ,
所以 在 上单调递增,又 ,所以 ,
即 ,所以 在 上单调递减,
所以 ,
所以 ,即 ,即 ,
当且仅当 ,即 时等号成立,
所以 的最小值为 .
【解析】本题考查利用导函数判断函数的单调性以及利用函数零点等已知求解最值,属于综合题.
导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极最值问题处理.
求出函数的导函数,再分 、 两种情况讨论,分别求出函数的单调性;
依题意可得 ,即可得到 ,从而得到 ,令 , ,令 , ,利用导数求出 的最小值,即可求出 的最小值.
第1页,共1页
同课章节目录
