2023-2024学年湖北省十堰市区县普通高中联合体高二(上)联考数学模拟试卷(12月份)(含解析)
文档属性
| 名称 | 2023-2024学年湖北省十堰市区县普通高中联合体高二(上)联考数学模拟试卷(12月份)(含解析) |  | |
| 格式 | Docx | ||
| 文件大小 | 178.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-14 23:05:07 | ||
图片预览




文档简介
2023-2024学年湖北省十堰市区县普通高中联合体高二(上)联考数学
模拟试卷(12月份)
一.选择题(共8小题,满分40分,每小题5分。在每小题所给出的四个选项中,只有一个选项符合题目要求。)
1.(5分)某居民小区有两个相互独立的安全防范系统A和B,系统A和系统B在任意时刻发生故障的概率分别为和p,已知两个系统至少有一个能正常运作,小区就处于安全防范状态若要求小区在任意时刻均处于安全防范状态的概率不低于,则p的最大值为( )
A. B. C. D.
2.(5分)若直线l的方向向量,平面β的法向量,则( )
A.l β B.l⊥β C.l∥β D.l β或l∥β
3.(5分)为弘扬传统文化,某校进行了书法大赛,同学们踊跃报名,在成绩公布之前,可以确定甲、乙、丙、丁、戊5名从小就练习书法的同学锁定了第1至5名.甲和乙去询问成绩,组委会对甲说:“很遗憾,你和乙都没有获得冠军.”对乙说:“你当然不会是五人中最差的.”则最终丙和丁获得前两名的概率为( )
A. B. C. D.
4.(5分)设直线l:3x+2y﹣6=0,P(m,n)为直线l上动点,则(m﹣1)2+n2的最小值为( )
A. B. C. D.
5.(5分)已知两条直线l1,l2的方向向量分别是(2,﹣3,1),(﹣1,1,5),则l1,l2的位置关系为( )
A.平行 B.垂直 C.相交 D.重合
6.(5分)已知双曲线与抛物线y2=8x的一个交点为P,F为抛物线的焦点,若|PF|=5,则双曲线的渐近线方程为( )
A.x±2y=0 B.2x±y=0 C. D.
7.(5分)平面直角坐标系中有两点O1(﹣1,0)和O2(1,0),以O1为圆心,正整数i为半径的圆记为Ai,以O2为圆心,正整数j为半径的圆记为Bj.对于正整数k(1≤k≤5),点Pk是圆Ak与圆Bk+1的交点,且P1,P2,P3,P4,P5都位于第二象限,则这5个点都在同一( )
A.直线上 B.椭圆上 C.抛物线上 D.双曲线上
8.(5分)设动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上,λ,当∠APC为锐角时,λ的取值范围是( )
A.[0,) B.[0,) C.(,1) D.(,1)
二.多选题(共4小题,满分20分,每小题5分)
(多选)9.(5分)某项科学素养测试规则为:系统随机抽取5道测试题目,规定:要求答题者达到等级评定要求或答完5道题方能结束测试.若答题者连续做对4道,则系统立即结束测试,并评定能力等级为A;若连续做错3道题目,则系统自动终止测试,评定能力等级为C;其它情形评定能力等级为B.已知小华同学做对每道题的概率均为,且他每道题是否答对相互独立,则以下说法正确的是( )
A.小华能力等级评定为A的概率为
B.小华能力等级评定为B的概率为
C.小华只做了4道题目的概率为
D.小华做完5道题目的概率为
(多选)10.(5分)以下四个命题表述正确的是( )
A.直线(3+m)x+4y﹣3+3m=0(m∈R)恒过定点(﹣3,﹣3)
B.圆x2+y2=4上有且仅有3个点到直线l:x﹣y0的距离都等于1
C.曲线C1:x2+y2+2x=0与曲线C2:x2+y2﹣4x﹣8y+m=0恰有三条公切线,则m=4
D.已知圆C:x2+y2=1,点P为直线x+2y=4上一动点,过点P向圆C引两条切线PA、PB,其中A、B为切点,则直线AB经过定点
(多选)11.(5分)正方体ABCD﹣A1B1C1D1的棱长为2,O为底面ABCD的中心,M为棱B1C1上的动点(不包含两个端点),则下列命题中错误的是( )
A.存在点M,使得A1D∥平面MOB
B.存在点M,使得A1D⊥平面MOB
C.存在点M,使得MO⊥BO
D.存在点M,使得A1D与BM所成角为
(多选)12.(5分)设抛物线C:y2=2px(p>0)的焦点为F,准线为l.过焦点F的直线交曲线C于P(x1,y1),Q(x2,y2)两点,则( )
A.以PF为直径的圆与准线l相切
B.以PQ为直径的圆与准线l相切
C.
D.
三.填空题(共4小题,满分20分,每小题5分)
13.(5分)某学校有教师150人,其中高级教师15人,中级教师45人,初级教师90人.现按职称分层抽样选出30名教师参加教工代表大会,则选出的高级教师的人数为
14.(5分)若直线 l1:ax+2y+6=0与直线 l2:x+(a﹣1)y+(a2﹣1)=0平行则实数 a= .
15.(5分)如图,⊙O1与⊙O2交于M、N两点,直线AE与这两个圆及MN依次交于A、B、C、D、E;且AD=19,BE=16,BC=4,则AE= .
16.(5分)已知双曲线C:(其中a>0,b>0)的焦距为,其中一条渐近线的斜率为2,则a= .
四.解答题(共6小题,满分70分)
17.(10分)在人寿保险事业中,很重视某一年龄段的投保人的死亡率.假如每个投保人能活到70岁的概率为0.6,求3个投保人中:
(1)全部活到70岁的概率;
(2)有2个活到70岁的概率;
(3)有1个活到70岁的概率.
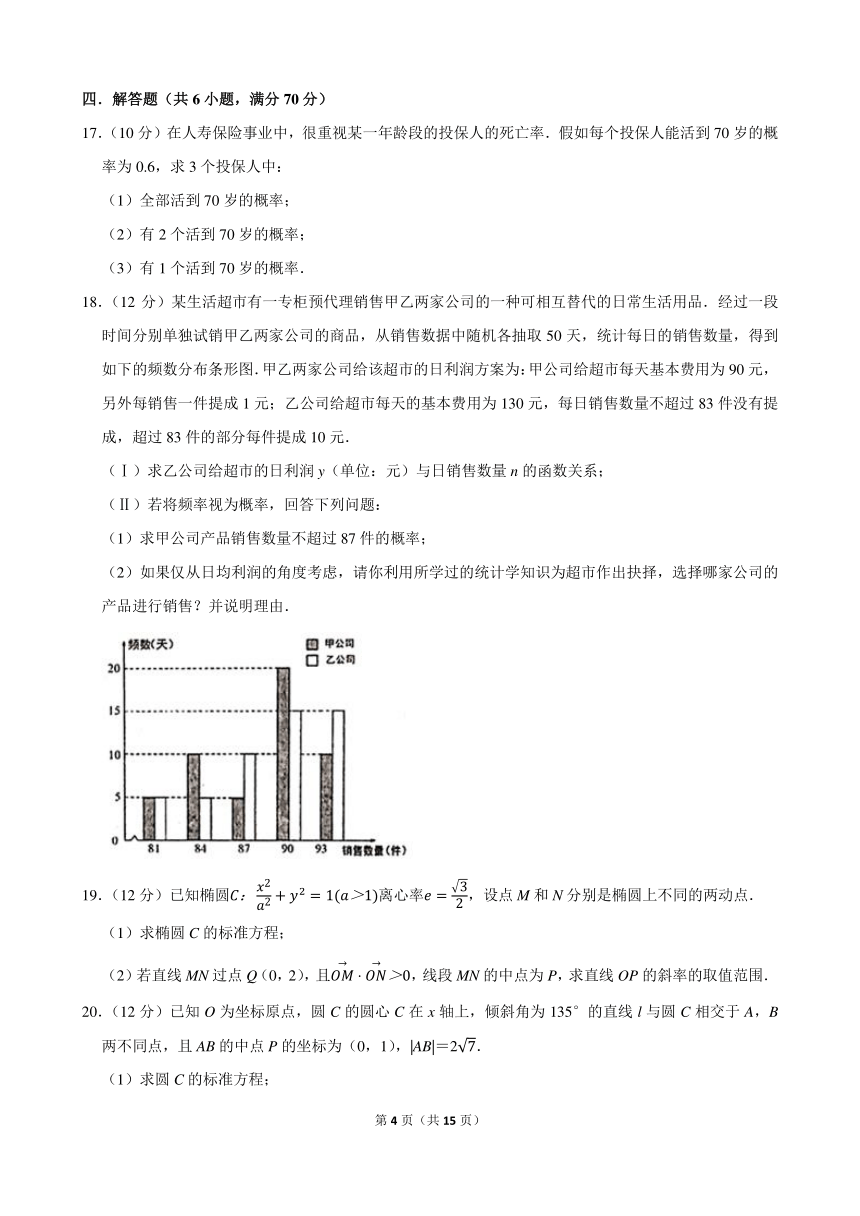
18.(12分)某生活超市有一专柜预代理销售甲乙两家公司的一种可相互替代的日常生活用品.经过一段时间分别单独试销甲乙两家公司的商品,从销售数据中随机各抽取50天,统计每日的销售数量,得到如下的频数分布条形图.甲乙两家公司给该超市的日利润方案为:甲公司给超市每天基本费用为90元,另外每销售一件提成1元;乙公司给超市每天的基本费用为130元,每日销售数量不超过83件没有提成,超过83件的部分每件提成10元.
(Ⅰ)求乙公司给超市的日利润y(单位:元)与日销售数量n的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
(1)求甲公司产品销售数量不超过87件的概率;
(2)如果仅从日均利润的角度考虑,请你利用所学过的统计学知识为超市作出抉择,选择哪家公司的产品进行销售?并说明理由.
19.(12分)已知椭圆离心率,设点M和N分别是椭圆上不同的两动点.
(1)求椭圆C的标准方程;
(2)若直线MN过点Q(0,2),且,线段MN的中点为P,求直线OP的斜率的取值范围.
20.(12分)已知O为坐标原点,圆C的圆心C在x轴上,倾斜角为135°的直线l与圆C相交于A,B两不同点,且AB的中点P的坐标为(0,1),|AB|=2.
(1)求圆C的标准方程;
(2)求过点Q(2,4)与圆C相切的直线的方程.
21.(12分)如图,在直三棱柱ABC﹣A1B1C1中、∠BAC=90°.AB=AC=AA1=2,E是BC中点.
(Ⅰ)求证:A1B∥平面AEC1;
(Ⅱ)在棱AA1存在一点M,满足B1M⊥C1E,求平面MEC1与平面ABB1A1夹角的余弦值.
22.(12分)已知椭圆C:(a>b>0)过点(0,1),离心率为.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过椭圆C上的点A(x0,y0)(x0y0≠0)的直线l与x,y轴的交点分别为M,N,且,过原点O的直线m与l平行,且与C交于B,D两点,求△ABD面积的最大值.
2023-2024学年湖北省十堰市区县普通高中联合体高二(上)联考数学模拟试卷(12月份)
答案与解析
一.选择题(共8小题,满分40分,每小题5分)
1.【解答】解:设系统A和系统B在任意时刻发生故障的事件分别为M和N,
则小区处于安全防范状态的概率为1﹣P(MN)=1,解得,
所以p的最大值为.
故选:A.
2.【解答】解:∵直线l的方向向量,
平面β的法向量,
1+0﹣1=0,
∴l β或l∥β.
故选:D.
3.【解答】解:由概率的相关性质,只需分析甲乙丙丁戊五人情况即可.
①若甲是最后一名,则乙可能是二、三、四名,剩下三人共有种情况,此时共有种情况;
②若甲不是最后一名,则甲乙需排在二、三、四名,有种情况,剩下三人共有种情况,此时有种情况.
则一共有36+18=54种不同的名次情况,
最终丙和丁获得前两名的情况有种,故丙和丁获得前两名的概率.
故选:D.
4.【解答】解:根据题意,(m﹣1)2+n2=(m﹣1)2+(n﹣0)2,其几何意义为点(m,n)与点(1,0)之间距离的平方,
而点(1,0)到直线l:3x+2y﹣6=0的距离d,
故(m﹣1)2+n2的最小值为,
故选:A.
5.【解答】解:∵(2,﹣3,1),(﹣1,1,5),
∴(﹣3)×1+1×5=0.
故l1,l2的位置关系为垂直.
故选:B.
6.【解答】解:∵点P在抛物线y2=8x上,|PF|=5,
∴P(x0,y0)满足x05,得x0=55﹣2=3
因此y02=8x0=24,得y0=±2
∴点P(3,±2)在双曲线上
可得91,解之得m=3
∴双曲线标准方程为,
得a=1,b,渐近线方程为y=±,即y=±x
故选:C.
7.【解答】解:根据题意,圆Ak是以O1(﹣1,0)为圆心,k为半径的圆,
圆Bk+1是以O2(1,0)为圆心,k+1为半径的圆,(1≤k≤5)
若点Pk是圆Ak与圆Bk+1的交点,则|PkO1|=k,|PkO2|=k+1,
则有|PkO2|﹣|PkO1|=1,而|O1O2|=2,(1≤k≤5),
则点Pk在以O1、O1为焦点,a的双曲线上,该双曲线的方程为1,
故P1,P2,P3,P4,P5都在同一个双曲线上,
故选:D.
8.【解答】解:建立如图所示的空间直角坐标系,
则A(1,0,0),C(0,1,0),B(1,1,0),D1(0,0,1),
由λ,可得P(λ,λ,1﹣λ),
则(1﹣λ,﹣λ,λ﹣1),(﹣λ,1﹣λ,λ﹣1),
因为∠APC为锐角,
所以(1﹣λ,﹣λ,λ﹣1) (﹣λ,1﹣λ,λ﹣1)=(λ﹣1)(3λ﹣1)>0,解得λ,或λ>1,
又因为动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上,
所以0,故λ的取值范围是[0,).
故选:A.
二.多选题(共4小题,满分20分,每小题5分)
9.【解答】解:小华能力等级评定为A,则需要连续做对4道题,所以,A正确;
小华能力等级评定为C,则他连续做错3道题目,有四种情况,
所以.
由题意小华能力等级评定为B的概率为,B正确;
小华做完3道题目结束测试的概率为,
小华做完5道题目的概率为,D不正确,
小华只做了4道题目有两种情况,一是4道题全对,二是第1题对了,后续3道题目全错,其概率为,C正确.
故选:ABC.
10.【解答】解:由(3+m)x+4y﹣3+3m=0(m∈R),得3x+4y﹣3+m(x+3)=0,
联立,解得,
∴直线(3+m)x+4y﹣3+3m=0(m∈R)恒过定点(﹣3,3),故A错误;
∵圆心(0,0)到直线l:x﹣y0的距离等于1,∴直线与圆相交,而圆的半径为2,
故到直线距离为1的两条直线,一条与圆相切,一条与圆相交,
因此圆上有三个点到直线l:x﹣y0的距离等于1,故B正确;
两圆有三条公切线,则两圆外切,曲线C1:x2+y2+2x=0化为标准式(x+1)2+y2=1,
曲线C2:x2+y2﹣4x﹣8y+m=0化为标准式(x﹣2)2+(y﹣4)2=20﹣m>0,
圆心距为5=1,解得m=4,故C正确;
设点P的坐标为(m,n),∴1,以OP为直径的圆的方程为x2+y2﹣mx﹣ny=0,
两圆的方程作差得直线AB的方程为:mx+ny=1,消去n得,m(x)+2y﹣1=0,
令x0,2y﹣1=0,解得x,y,故直线AB经过定点(,),故D正确.
故选:BCD.
11.【解答】解:如图,连接A1B,BD,建立如图所示的空间直角坐标系,则O(1,1,0),B(2,2,0),
A1(2,0,2),D(0,0,0),设M(t,2,2)(0<t<2),
选项A,易知BD 平面MOB,故A1D与平面MOB有交点D,所以不存在点M,使得A1D∥平面MOB,A错误;
对于B,在正方体中,易知A1D=A1B=BD,故△A1BD为等边三角形,
所以∠A1DB=60°,所以不存在点M,使得A1D⊥平面MOB,故选项B错误;
选项C,(1﹣t,﹣1,﹣2),(﹣1,﹣1,0),由0,得到t=0,
所以MO⊥BO时,点M与C1重合,由条件知,不存在点M,使得MO⊥BO,故选项C错误;
选项D,因为(﹣2,0,﹣2),(t﹣2,0,2),
由|cos,|cos,得到,
化简得到t2+4t﹣8=0,得到或,
因为,所以存在点M,使得 A1D与BM所成角为,故选项D正确;
故选:ABC.
12.【解答】解:抛物线C:y2=2px(p>0)的焦点为F(,0),准线为l:x,PF的中点M(,),直径|PF|=x1,
点M到准线的距离为dx1p|PF|,所以以PF为直径的圆与准线l不相切,故A错误;
焦点弦|PQ|=x1+x2+p,M(,)为PQ的中点,则M到准线l的距离d,
则以PQ为直径的圆与抛物线C的准线相切,故B正确;
易知直线PQ的斜率不为0,故可设直线PQ的方程为x=my,代入抛物线方程得y2﹣2mpy﹣p2=0,
由韦达定理有y1+y2=2mp,y1y2=﹣p2,所以x1x2,故C正确;
又x1+x2=my1my2m(y1+y2)+p=2mp2+p,
所以,故D正确.
故选:BCD.
三.填空题(共4小题,满分20分,每小题5分)
13.【解答】解:∵有教师150人,现按职称分层抽样选出30名教师参加教工代表大会,
∴每个个体被抽到的概率是,
∴高级教师被抽到的人数是3,
故答案为:3.
14.【解答】解:∵直线l1:ax+2y+6=0与直线l2:x+(a﹣1)y+(a2﹣1)=0平行,
∴a(a﹣1)﹣2×1=0,解得a=﹣1或 a=2,
经验证当a=2时,直线重合,a=﹣1符合题意.
故答案为:﹣1.
15.【解答】解:因为A,M,D,N四点共圆,所以AC CD=MC CN.同理,有BC CE=MC CN.
所以AC CD=BC CE,即(AB+BC) CD=BC (CD+CE),
所以AB CD=BC DE.
设CD=x,则AB=AD﹣BC﹣CD=19﹣4﹣x=15﹣x,DE=BE﹣BC﹣CD=16﹣4﹣x=12﹣x,
则(15﹣x)x=4(12﹣x),即x2﹣19x+48=0,解得x=3或x=16(舍).
AE=AB+DE﹣BD=19+16﹣7=28.
故答案为:28
16.【解答】解:由,得.
故答案为:2.
四.解答题(共6小题,满分70分)
17.【解答】解:每个投保人能活到70岁的概率为0.6,活到70岁以下的概率为,
(1)设“全部活到70岁”为事件A,
P(A);
(2)设“有2个活到70岁”为事件B,
P(B);
(3)设“有1个活到70岁”为事件C,
P(C).
18.【解答】解:(Ⅰ)由题意:当0≤n≤83时,y=130元;
当n>83时,y=130+(n﹣83)×10=10n﹣700.
∴乙公司给超市的日利润y(单位:元)与销售数量n的函数关系为:.
(Ⅱ)(1)记事件A:“甲公司产品的销售数量不超过87件”,
则甲公司产品销售数量不超过87件的概率为;
(2)甲公司的给超市的日利润为X(单位:元),
则X的所有可能取值为171,174,177,180,183,
(元),
设乙公司给超市的日利润为Y元,则Y的所有可能取值为130,140,170,200,230,
则(元),
由于,所以超市应代理销售乙公司的产品较为合适.
19.【解答】解:(1)易知,
所以,
解得a2=4,
则椭圆C的标准方程为;
(2)易知直线MN的斜率存在且不为0,
不妨设直线MN的方程为y=kx+2,M(x1,y1),N(x2,y2),
联立,消去y并整理得(1+4k2)x2+16kx+12=0,
此时Δ=(16k)2﹣4×(1+4k2)×12=16(4k2﹣3)>0,
解得,
由韦达定理得,
所以,
因为,
所以,
解得k2<4,
即﹣2<k或k<2,
不妨设直线OP的斜率为k′,
因为M,N两点都在椭圆上,
所以,
两式相减得,
即,
则,
故直线OP的斜率的取值范围为.
20.【解答】解:(1)设所求圆的圆心坐标为(a,0),
由倾斜角为135°的直线l与圆C相交于A,B两不同点,且AB的中点P的坐标为(0,1),
则,
即a=﹣1,
即C(﹣1,0),
则|CP|,
又|AB|=2,
则圆的半径为,
即圆C的标准方程为(x+1)2+y2=9;
(2)①当所求直线斜率存在时,
不妨设为y=k(x﹣2)+4,
则,
即k,
即所求直线为y(x﹣2)+4,
即7x﹣24y+82=0,
②当所求直线斜率不存在时,
显然直线x=2满足题意,
即过点Q(2,4)与圆C相切的直线的方程为7x﹣24y+82=0或x=2.
21.【解答】(Ⅰ)证明:连接A1C交AC1于D,
∵四边形ACC1A1是平行四边形,
∴D是A1C的中点,又E是BC的中点,
∴DE∥A1B,又A1B 平面AEC1,DE 平面AEC1,
∴A1B∥平面AEC1.
(Ⅱ)解:以A为原点,以AB,AC,AA1为坐标轴建立空间直角坐标系A﹣xyz,
设AM=h,则B1(2,0,2),M(0,0,h),C1(0,2,2),E(1,1,0),
∴(﹣2,0,h﹣2),(1,﹣1,﹣2),
∵B1M⊥C1E,∴0,即﹣2﹣2(h﹣2)=0,∴h=1,故M(0,0,1),∴(﹣1,﹣1,1),
设平面MEC1的法向量为(x,y,z),则,即,
令z=2可得(3,﹣1,2),
又(0,1,0)为平面ABB1A1的一个法向量,
∴cos,,
∴平面MEC1与平面ABB1A1夹角的余弦值为.
22.【解答】解:(Ⅰ)由题意得b=1,又
所以a=2
∴椭圆C的标准方程为.
(Ⅱ)∵点A在椭圆上,∴,即
由题意可得直线l的斜率存在且不为0,
设直线l的方程为y﹣y0=k(x﹣x0)(k≠0),
则,
则.
,即,
∴直线l的斜率
∵BD∥l,
∴直线BD的方程为,即y0x+2x0y=0.
联立,解得,∴,
∴,
又点A到直线BD的距离
,
∴,
又,
当且仅当,即时等号成立,
∴,
∴
∴0<S△ABD≤2.
∴△ABD面积的最大值为2.
第1页(共1页)
模拟试卷(12月份)
一.选择题(共8小题,满分40分,每小题5分。在每小题所给出的四个选项中,只有一个选项符合题目要求。)
1.(5分)某居民小区有两个相互独立的安全防范系统A和B,系统A和系统B在任意时刻发生故障的概率分别为和p,已知两个系统至少有一个能正常运作,小区就处于安全防范状态若要求小区在任意时刻均处于安全防范状态的概率不低于,则p的最大值为( )
A. B. C. D.
2.(5分)若直线l的方向向量,平面β的法向量,则( )
A.l β B.l⊥β C.l∥β D.l β或l∥β
3.(5分)为弘扬传统文化,某校进行了书法大赛,同学们踊跃报名,在成绩公布之前,可以确定甲、乙、丙、丁、戊5名从小就练习书法的同学锁定了第1至5名.甲和乙去询问成绩,组委会对甲说:“很遗憾,你和乙都没有获得冠军.”对乙说:“你当然不会是五人中最差的.”则最终丙和丁获得前两名的概率为( )
A. B. C. D.
4.(5分)设直线l:3x+2y﹣6=0,P(m,n)为直线l上动点,则(m﹣1)2+n2的最小值为( )
A. B. C. D.
5.(5分)已知两条直线l1,l2的方向向量分别是(2,﹣3,1),(﹣1,1,5),则l1,l2的位置关系为( )
A.平行 B.垂直 C.相交 D.重合
6.(5分)已知双曲线与抛物线y2=8x的一个交点为P,F为抛物线的焦点,若|PF|=5,则双曲线的渐近线方程为( )
A.x±2y=0 B.2x±y=0 C. D.
7.(5分)平面直角坐标系中有两点O1(﹣1,0)和O2(1,0),以O1为圆心,正整数i为半径的圆记为Ai,以O2为圆心,正整数j为半径的圆记为Bj.对于正整数k(1≤k≤5),点Pk是圆Ak与圆Bk+1的交点,且P1,P2,P3,P4,P5都位于第二象限,则这5个点都在同一( )
A.直线上 B.椭圆上 C.抛物线上 D.双曲线上
8.(5分)设动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上,λ,当∠APC为锐角时,λ的取值范围是( )
A.[0,) B.[0,) C.(,1) D.(,1)
二.多选题(共4小题,满分20分,每小题5分)
(多选)9.(5分)某项科学素养测试规则为:系统随机抽取5道测试题目,规定:要求答题者达到等级评定要求或答完5道题方能结束测试.若答题者连续做对4道,则系统立即结束测试,并评定能力等级为A;若连续做错3道题目,则系统自动终止测试,评定能力等级为C;其它情形评定能力等级为B.已知小华同学做对每道题的概率均为,且他每道题是否答对相互独立,则以下说法正确的是( )
A.小华能力等级评定为A的概率为
B.小华能力等级评定为B的概率为
C.小华只做了4道题目的概率为
D.小华做完5道题目的概率为
(多选)10.(5分)以下四个命题表述正确的是( )
A.直线(3+m)x+4y﹣3+3m=0(m∈R)恒过定点(﹣3,﹣3)
B.圆x2+y2=4上有且仅有3个点到直线l:x﹣y0的距离都等于1
C.曲线C1:x2+y2+2x=0与曲线C2:x2+y2﹣4x﹣8y+m=0恰有三条公切线,则m=4
D.已知圆C:x2+y2=1,点P为直线x+2y=4上一动点,过点P向圆C引两条切线PA、PB,其中A、B为切点,则直线AB经过定点
(多选)11.(5分)正方体ABCD﹣A1B1C1D1的棱长为2,O为底面ABCD的中心,M为棱B1C1上的动点(不包含两个端点),则下列命题中错误的是( )
A.存在点M,使得A1D∥平面MOB
B.存在点M,使得A1D⊥平面MOB
C.存在点M,使得MO⊥BO
D.存在点M,使得A1D与BM所成角为
(多选)12.(5分)设抛物线C:y2=2px(p>0)的焦点为F,准线为l.过焦点F的直线交曲线C于P(x1,y1),Q(x2,y2)两点,则( )
A.以PF为直径的圆与准线l相切
B.以PQ为直径的圆与准线l相切
C.
D.
三.填空题(共4小题,满分20分,每小题5分)
13.(5分)某学校有教师150人,其中高级教师15人,中级教师45人,初级教师90人.现按职称分层抽样选出30名教师参加教工代表大会,则选出的高级教师的人数为
14.(5分)若直线 l1:ax+2y+6=0与直线 l2:x+(a﹣1)y+(a2﹣1)=0平行则实数 a= .
15.(5分)如图,⊙O1与⊙O2交于M、N两点,直线AE与这两个圆及MN依次交于A、B、C、D、E;且AD=19,BE=16,BC=4,则AE= .
16.(5分)已知双曲线C:(其中a>0,b>0)的焦距为,其中一条渐近线的斜率为2,则a= .
四.解答题(共6小题,满分70分)
17.(10分)在人寿保险事业中,很重视某一年龄段的投保人的死亡率.假如每个投保人能活到70岁的概率为0.6,求3个投保人中:
(1)全部活到70岁的概率;
(2)有2个活到70岁的概率;
(3)有1个活到70岁的概率.
18.(12分)某生活超市有一专柜预代理销售甲乙两家公司的一种可相互替代的日常生活用品.经过一段时间分别单独试销甲乙两家公司的商品,从销售数据中随机各抽取50天,统计每日的销售数量,得到如下的频数分布条形图.甲乙两家公司给该超市的日利润方案为:甲公司给超市每天基本费用为90元,另外每销售一件提成1元;乙公司给超市每天的基本费用为130元,每日销售数量不超过83件没有提成,超过83件的部分每件提成10元.
(Ⅰ)求乙公司给超市的日利润y(单位:元)与日销售数量n的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
(1)求甲公司产品销售数量不超过87件的概率;
(2)如果仅从日均利润的角度考虑,请你利用所学过的统计学知识为超市作出抉择,选择哪家公司的产品进行销售?并说明理由.
19.(12分)已知椭圆离心率,设点M和N分别是椭圆上不同的两动点.
(1)求椭圆C的标准方程;
(2)若直线MN过点Q(0,2),且,线段MN的中点为P,求直线OP的斜率的取值范围.
20.(12分)已知O为坐标原点,圆C的圆心C在x轴上,倾斜角为135°的直线l与圆C相交于A,B两不同点,且AB的中点P的坐标为(0,1),|AB|=2.
(1)求圆C的标准方程;
(2)求过点Q(2,4)与圆C相切的直线的方程.
21.(12分)如图,在直三棱柱ABC﹣A1B1C1中、∠BAC=90°.AB=AC=AA1=2,E是BC中点.
(Ⅰ)求证:A1B∥平面AEC1;
(Ⅱ)在棱AA1存在一点M,满足B1M⊥C1E,求平面MEC1与平面ABB1A1夹角的余弦值.
22.(12分)已知椭圆C:(a>b>0)过点(0,1),离心率为.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过椭圆C上的点A(x0,y0)(x0y0≠0)的直线l与x,y轴的交点分别为M,N,且,过原点O的直线m与l平行,且与C交于B,D两点,求△ABD面积的最大值.
2023-2024学年湖北省十堰市区县普通高中联合体高二(上)联考数学模拟试卷(12月份)
答案与解析
一.选择题(共8小题,满分40分,每小题5分)
1.【解答】解:设系统A和系统B在任意时刻发生故障的事件分别为M和N,
则小区处于安全防范状态的概率为1﹣P(MN)=1,解得,
所以p的最大值为.
故选:A.
2.【解答】解:∵直线l的方向向量,
平面β的法向量,
1+0﹣1=0,
∴l β或l∥β.
故选:D.
3.【解答】解:由概率的相关性质,只需分析甲乙丙丁戊五人情况即可.
①若甲是最后一名,则乙可能是二、三、四名,剩下三人共有种情况,此时共有种情况;
②若甲不是最后一名,则甲乙需排在二、三、四名,有种情况,剩下三人共有种情况,此时有种情况.
则一共有36+18=54种不同的名次情况,
最终丙和丁获得前两名的情况有种,故丙和丁获得前两名的概率.
故选:D.
4.【解答】解:根据题意,(m﹣1)2+n2=(m﹣1)2+(n﹣0)2,其几何意义为点(m,n)与点(1,0)之间距离的平方,
而点(1,0)到直线l:3x+2y﹣6=0的距离d,
故(m﹣1)2+n2的最小值为,
故选:A.
5.【解答】解:∵(2,﹣3,1),(﹣1,1,5),
∴(﹣3)×1+1×5=0.
故l1,l2的位置关系为垂直.
故选:B.
6.【解答】解:∵点P在抛物线y2=8x上,|PF|=5,
∴P(x0,y0)满足x05,得x0=55﹣2=3
因此y02=8x0=24,得y0=±2
∴点P(3,±2)在双曲线上
可得91,解之得m=3
∴双曲线标准方程为,
得a=1,b,渐近线方程为y=±,即y=±x
故选:C.
7.【解答】解:根据题意,圆Ak是以O1(﹣1,0)为圆心,k为半径的圆,
圆Bk+1是以O2(1,0)为圆心,k+1为半径的圆,(1≤k≤5)
若点Pk是圆Ak与圆Bk+1的交点,则|PkO1|=k,|PkO2|=k+1,
则有|PkO2|﹣|PkO1|=1,而|O1O2|=2,(1≤k≤5),
则点Pk在以O1、O1为焦点,a的双曲线上,该双曲线的方程为1,
故P1,P2,P3,P4,P5都在同一个双曲线上,
故选:D.
8.【解答】解:建立如图所示的空间直角坐标系,
则A(1,0,0),C(0,1,0),B(1,1,0),D1(0,0,1),
由λ,可得P(λ,λ,1﹣λ),
则(1﹣λ,﹣λ,λ﹣1),(﹣λ,1﹣λ,λ﹣1),
因为∠APC为锐角,
所以(1﹣λ,﹣λ,λ﹣1) (﹣λ,1﹣λ,λ﹣1)=(λ﹣1)(3λ﹣1)>0,解得λ,或λ>1,
又因为动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上,
所以0,故λ的取值范围是[0,).
故选:A.
二.多选题(共4小题,满分20分,每小题5分)
9.【解答】解:小华能力等级评定为A,则需要连续做对4道题,所以,A正确;
小华能力等级评定为C,则他连续做错3道题目,有四种情况,
所以.
由题意小华能力等级评定为B的概率为,B正确;
小华做完3道题目结束测试的概率为,
小华做完5道题目的概率为,D不正确,
小华只做了4道题目有两种情况,一是4道题全对,二是第1题对了,后续3道题目全错,其概率为,C正确.
故选:ABC.
10.【解答】解:由(3+m)x+4y﹣3+3m=0(m∈R),得3x+4y﹣3+m(x+3)=0,
联立,解得,
∴直线(3+m)x+4y﹣3+3m=0(m∈R)恒过定点(﹣3,3),故A错误;
∵圆心(0,0)到直线l:x﹣y0的距离等于1,∴直线与圆相交,而圆的半径为2,
故到直线距离为1的两条直线,一条与圆相切,一条与圆相交,
因此圆上有三个点到直线l:x﹣y0的距离等于1,故B正确;
两圆有三条公切线,则两圆外切,曲线C1:x2+y2+2x=0化为标准式(x+1)2+y2=1,
曲线C2:x2+y2﹣4x﹣8y+m=0化为标准式(x﹣2)2+(y﹣4)2=20﹣m>0,
圆心距为5=1,解得m=4,故C正确;
设点P的坐标为(m,n),∴1,以OP为直径的圆的方程为x2+y2﹣mx﹣ny=0,
两圆的方程作差得直线AB的方程为:mx+ny=1,消去n得,m(x)+2y﹣1=0,
令x0,2y﹣1=0,解得x,y,故直线AB经过定点(,),故D正确.
故选:BCD.
11.【解答】解:如图,连接A1B,BD,建立如图所示的空间直角坐标系,则O(1,1,0),B(2,2,0),
A1(2,0,2),D(0,0,0),设M(t,2,2)(0<t<2),
选项A,易知BD 平面MOB,故A1D与平面MOB有交点D,所以不存在点M,使得A1D∥平面MOB,A错误;
对于B,在正方体中,易知A1D=A1B=BD,故△A1BD为等边三角形,
所以∠A1DB=60°,所以不存在点M,使得A1D⊥平面MOB,故选项B错误;
选项C,(1﹣t,﹣1,﹣2),(﹣1,﹣1,0),由0,得到t=0,
所以MO⊥BO时,点M与C1重合,由条件知,不存在点M,使得MO⊥BO,故选项C错误;
选项D,因为(﹣2,0,﹣2),(t﹣2,0,2),
由|cos,|cos,得到,
化简得到t2+4t﹣8=0,得到或,
因为,所以存在点M,使得 A1D与BM所成角为,故选项D正确;
故选:ABC.
12.【解答】解:抛物线C:y2=2px(p>0)的焦点为F(,0),准线为l:x,PF的中点M(,),直径|PF|=x1,
点M到准线的距离为dx1p|PF|,所以以PF为直径的圆与准线l不相切,故A错误;
焦点弦|PQ|=x1+x2+p,M(,)为PQ的中点,则M到准线l的距离d,
则以PQ为直径的圆与抛物线C的准线相切,故B正确;
易知直线PQ的斜率不为0,故可设直线PQ的方程为x=my,代入抛物线方程得y2﹣2mpy﹣p2=0,
由韦达定理有y1+y2=2mp,y1y2=﹣p2,所以x1x2,故C正确;
又x1+x2=my1my2m(y1+y2)+p=2mp2+p,
所以,故D正确.
故选:BCD.
三.填空题(共4小题,满分20分,每小题5分)
13.【解答】解:∵有教师150人,现按职称分层抽样选出30名教师参加教工代表大会,
∴每个个体被抽到的概率是,
∴高级教师被抽到的人数是3,
故答案为:3.
14.【解答】解:∵直线l1:ax+2y+6=0与直线l2:x+(a﹣1)y+(a2﹣1)=0平行,
∴a(a﹣1)﹣2×1=0,解得a=﹣1或 a=2,
经验证当a=2时,直线重合,a=﹣1符合题意.
故答案为:﹣1.
15.【解答】解:因为A,M,D,N四点共圆,所以AC CD=MC CN.同理,有BC CE=MC CN.
所以AC CD=BC CE,即(AB+BC) CD=BC (CD+CE),
所以AB CD=BC DE.
设CD=x,则AB=AD﹣BC﹣CD=19﹣4﹣x=15﹣x,DE=BE﹣BC﹣CD=16﹣4﹣x=12﹣x,
则(15﹣x)x=4(12﹣x),即x2﹣19x+48=0,解得x=3或x=16(舍).
AE=AB+DE﹣BD=19+16﹣7=28.
故答案为:28
16.【解答】解:由,得.
故答案为:2.
四.解答题(共6小题,满分70分)
17.【解答】解:每个投保人能活到70岁的概率为0.6,活到70岁以下的概率为,
(1)设“全部活到70岁”为事件A,
P(A);
(2)设“有2个活到70岁”为事件B,
P(B);
(3)设“有1个活到70岁”为事件C,
P(C).
18.【解答】解:(Ⅰ)由题意:当0≤n≤83时,y=130元;
当n>83时,y=130+(n﹣83)×10=10n﹣700.
∴乙公司给超市的日利润y(单位:元)与销售数量n的函数关系为:.
(Ⅱ)(1)记事件A:“甲公司产品的销售数量不超过87件”,
则甲公司产品销售数量不超过87件的概率为;
(2)甲公司的给超市的日利润为X(单位:元),
则X的所有可能取值为171,174,177,180,183,
(元),
设乙公司给超市的日利润为Y元,则Y的所有可能取值为130,140,170,200,230,
则(元),
由于,所以超市应代理销售乙公司的产品较为合适.
19.【解答】解:(1)易知,
所以,
解得a2=4,
则椭圆C的标准方程为;
(2)易知直线MN的斜率存在且不为0,
不妨设直线MN的方程为y=kx+2,M(x1,y1),N(x2,y2),
联立,消去y并整理得(1+4k2)x2+16kx+12=0,
此时Δ=(16k)2﹣4×(1+4k2)×12=16(4k2﹣3)>0,
解得,
由韦达定理得,
所以,
因为,
所以,
解得k2<4,
即﹣2<k或k<2,
不妨设直线OP的斜率为k′,
因为M,N两点都在椭圆上,
所以,
两式相减得,
即,
则,
故直线OP的斜率的取值范围为.
20.【解答】解:(1)设所求圆的圆心坐标为(a,0),
由倾斜角为135°的直线l与圆C相交于A,B两不同点,且AB的中点P的坐标为(0,1),
则,
即a=﹣1,
即C(﹣1,0),
则|CP|,
又|AB|=2,
则圆的半径为,
即圆C的标准方程为(x+1)2+y2=9;
(2)①当所求直线斜率存在时,
不妨设为y=k(x﹣2)+4,
则,
即k,
即所求直线为y(x﹣2)+4,
即7x﹣24y+82=0,
②当所求直线斜率不存在时,
显然直线x=2满足题意,
即过点Q(2,4)与圆C相切的直线的方程为7x﹣24y+82=0或x=2.
21.【解答】(Ⅰ)证明:连接A1C交AC1于D,
∵四边形ACC1A1是平行四边形,
∴D是A1C的中点,又E是BC的中点,
∴DE∥A1B,又A1B 平面AEC1,DE 平面AEC1,
∴A1B∥平面AEC1.
(Ⅱ)解:以A为原点,以AB,AC,AA1为坐标轴建立空间直角坐标系A﹣xyz,
设AM=h,则B1(2,0,2),M(0,0,h),C1(0,2,2),E(1,1,0),
∴(﹣2,0,h﹣2),(1,﹣1,﹣2),
∵B1M⊥C1E,∴0,即﹣2﹣2(h﹣2)=0,∴h=1,故M(0,0,1),∴(﹣1,﹣1,1),
设平面MEC1的法向量为(x,y,z),则,即,
令z=2可得(3,﹣1,2),
又(0,1,0)为平面ABB1A1的一个法向量,
∴cos,,
∴平面MEC1与平面ABB1A1夹角的余弦值为.
22.【解答】解:(Ⅰ)由题意得b=1,又
所以a=2
∴椭圆C的标准方程为.
(Ⅱ)∵点A在椭圆上,∴,即
由题意可得直线l的斜率存在且不为0,
设直线l的方程为y﹣y0=k(x﹣x0)(k≠0),
则,
则.
,即,
∴直线l的斜率
∵BD∥l,
∴直线BD的方程为,即y0x+2x0y=0.
联立,解得,∴,
∴,
又点A到直线BD的距离
,
∴,
又,
当且仅当,即时等号成立,
∴,
∴
∴0<S△ABD≤2.
∴△ABD面积的最大值为2.
第1页(共1页)
同课章节目录
