2024年九年级中考数学一轮复习专项练习题:相似(含答案)
文档属性
| 名称 | 2024年九年级中考数学一轮复习专项练习题:相似(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 141.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 10:39:33 | ||
图片预览

文档简介
2024年九年级中考数学一轮复习专项练习题:相似
一、单选题
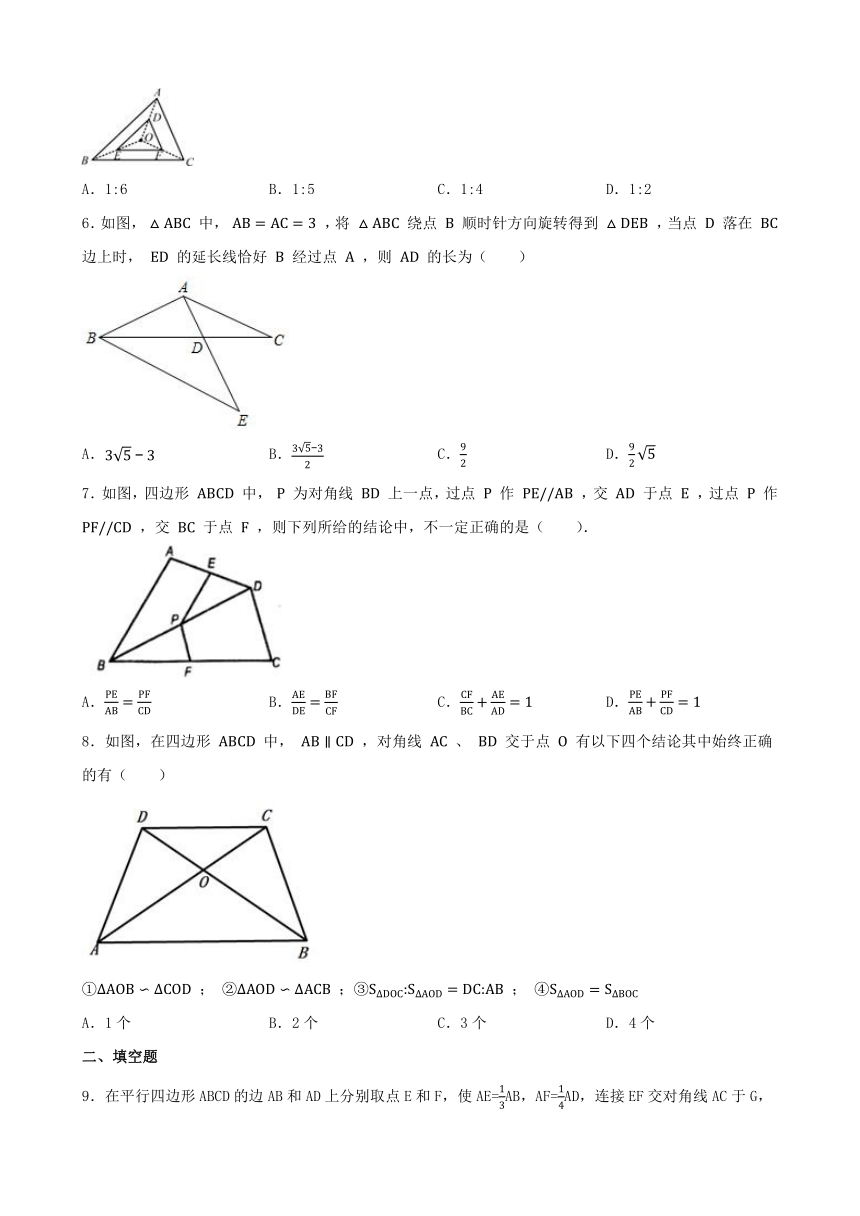
1.下列说法正确的是( )
A.各有一个角是70°的等腰三角形相似
B.各有一个角是95°的等腰三角形相似
C.所有的矩形相似
D.所有的菱形相似
2.如图,在 中, , , , ,则 的长为( )
A.1 B.2 C.4 D.6
3.如图,△ABC中,D、E分别为AC、BC边上的点,AB∥DE,CF为AB边上的中线,若AD=5,CD=3,DE=4,则BF的长为( )
A. B. C. D.
4.如图,在三角形ABC中,M,N分别是边AB,AC上的点,AM= AB,AN= AC,则三角形AMN的面积与四边形MBCN的面积比( )
A. B. C. D.
5.如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA, OB, OC的中点, 则△DEF与△ABC的面积比是( )
A.1:6 B.1:5 C.1:4 D.1:2
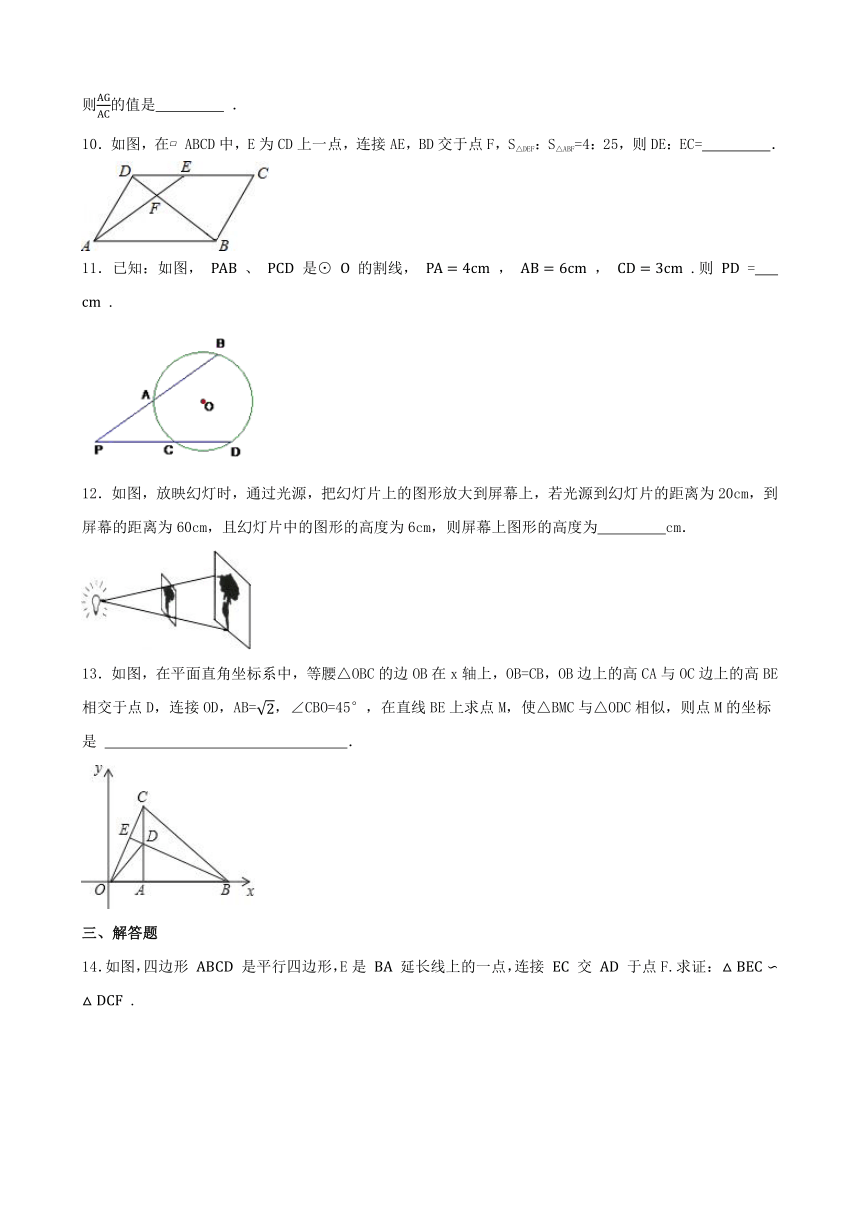
6.如图, 中, ,将 绕点 顺时针方向旋转得到 ,当点 落在 边上时, 的延长线恰好 经过点 ,则 的长为( )
A. B. C. D.
7.如图,四边形 中, 为对角线 上一点,过点 作 ,交 于点 ,过点 作 ,交 于点 ,则下列所给的结论中,不一定正确的是( ).
A. B. C. D.
8.如图,在四边形 中, ,对角线 、 交于点 有以下四个结论其中始终正确的有( )
① ; ② ;③ ; ④
A.1个 B.2个 C.3个 D.4个
二、填空题
9.在平行四边形ABCD的边AB和AD上分别取点E和F,使AE=AB,AF=AD,连接EF交对角线AC于G,则的值是 .
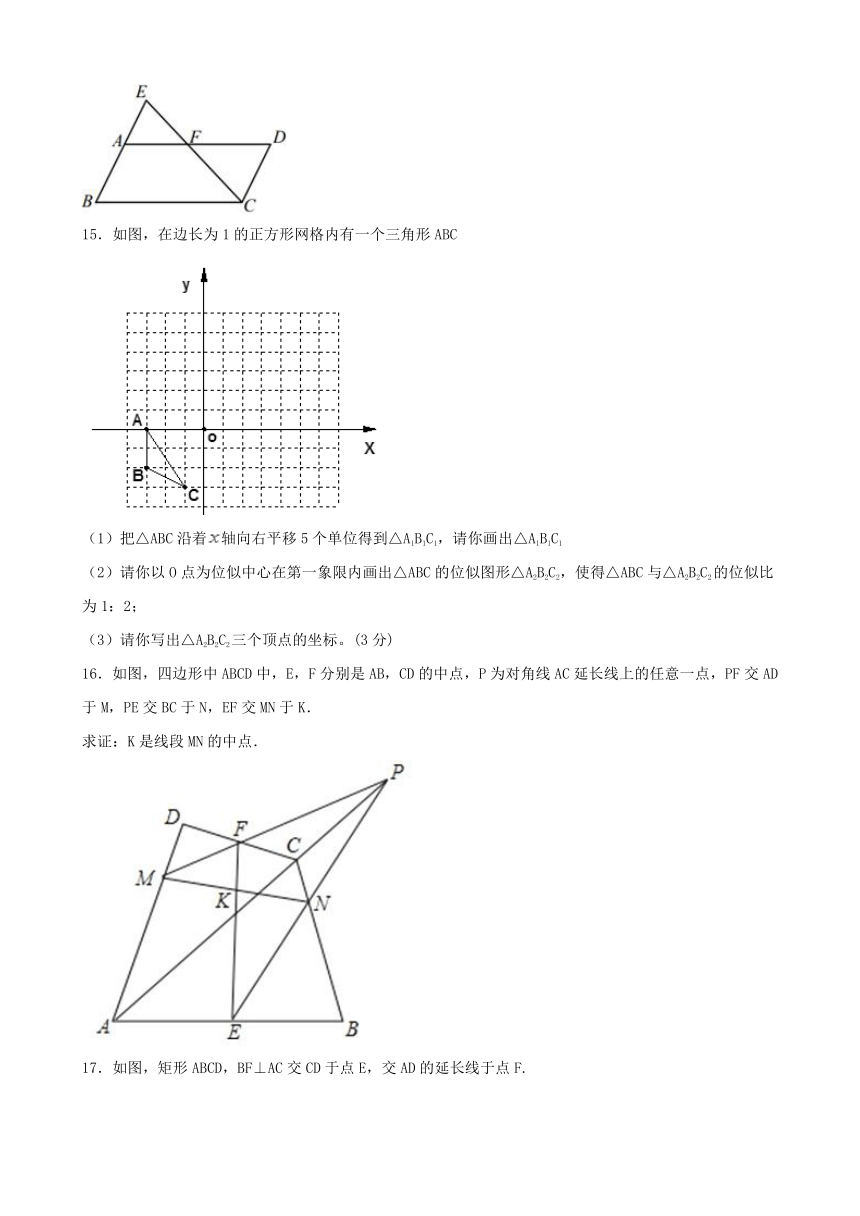
10.如图,在 ABCD中,E为CD上一点,连接AE,BD交于点F,S△DEF:S△ABF=4:25,则DE:EC= .
11.已知:如图, 、 是⊙ 的割线, , , .则 = .
12.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为 cm.
13.如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是 .
三、解答题
14.如图,四边形 是平行四边形,E是 延长线上的一点,连接 交 于点F.求证: .
15.如图,在边长为1的正方形网格内有一个三角形ABC
(1)把△ABC沿着轴向右平移5个单位得到△A1B1C1,请你画出△A1B1C1
(2)请你以O点为位似中心在第一象限内画出△ABC的位似图形△A2B2C2,使得△ABC与△A2B2C2的位似比为1:2;
(3)请你写出△A2B2C2三个顶点的坐标。(3分)
16.如图,四边形中ABCD中,E,F分别是AB,CD的中点,P为对角线AC延长线上的任意一点,PF交AD于M,PE交BC于N,EF交MN于K.
求证:K是线段MN的中点.
17.如图,矩形ABCD,BF⊥AC交CD于点E,交AD的延长线于点F.
(1)求证:AB2=BC·AF.
(2)当=,DF=5时,求AC的长.
18.如图, 是 的直径,点D在半径 上(D与O、A不重合), ,且 .连接 ,与 交于点F,在 上取一点E,使 .
(1)求证: 是 的切线;
(2)若D是 的中点, ,求 的长.
参考答案
1.B
2.D
3.B
4.B
5.C
6.B
7.A
8.C
9.
10.2:3
11.8
12.18
13.(1,)或(,)
14.证明:∵四边形 是平行四边形
∴ ,
∴
在 和 中
∵ ,
∴ .
15.解;(1)如图所示,△A1B1C1为所求的三角形;
(2)如图所示,△A2B2C2为所求的三角形;
(3)根据图形得:A2(6,0),B2(6,4),C2(2,6).
16.证明:∵EF截△PMN,
则(1)
∵BC截△PAE,
则(2),
∴即有,
所以(3),
∵CD截△PMA,
则,
即,∴(4)
因AP=AC+CP,得2CP+AC=2AP﹣AC,由(3),(4)得,
,
即 ,
所以由(1)得NK=KM,即K是线段MN的中点.
17.(1)证明:∵矩形ABCD
∴∠FAB=∠ABC=90°
∵BF⊥AC
∴∠ACB+∠CBE=∠CBE+∠FBA=90°
∴∠ACB=∠FBA
∴△ABF∽△BCA
∴
∴
(2)解:∵
∴设BC=2x,AB=3x
∵
∴
∴
∴BC=4, AB=6
∴
18.(1)证明:如图,连接 ,
∵ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∵ 为 的半径,
∴ 是 的切线;
(2)解:连接 ,如图,
∵ 是 的直径,
∴ ,
∵D是 的中点,
∴ ,
∴ ,
∵ , ,
∴ ,由勾股定理得: ,
∵ , ,
∴ ,
∴ ,
∴ ,
∴
一、单选题
1.下列说法正确的是( )
A.各有一个角是70°的等腰三角形相似
B.各有一个角是95°的等腰三角形相似
C.所有的矩形相似
D.所有的菱形相似
2.如图,在 中, , , , ,则 的长为( )
A.1 B.2 C.4 D.6
3.如图,△ABC中,D、E分别为AC、BC边上的点,AB∥DE,CF为AB边上的中线,若AD=5,CD=3,DE=4,则BF的长为( )
A. B. C. D.
4.如图,在三角形ABC中,M,N分别是边AB,AC上的点,AM= AB,AN= AC,则三角形AMN的面积与四边形MBCN的面积比( )
A. B. C. D.
5.如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA, OB, OC的中点, 则△DEF与△ABC的面积比是( )
A.1:6 B.1:5 C.1:4 D.1:2
6.如图, 中, ,将 绕点 顺时针方向旋转得到 ,当点 落在 边上时, 的延长线恰好 经过点 ,则 的长为( )
A. B. C. D.
7.如图,四边形 中, 为对角线 上一点,过点 作 ,交 于点 ,过点 作 ,交 于点 ,则下列所给的结论中,不一定正确的是( ).
A. B. C. D.
8.如图,在四边形 中, ,对角线 、 交于点 有以下四个结论其中始终正确的有( )
① ; ② ;③ ; ④
A.1个 B.2个 C.3个 D.4个
二、填空题
9.在平行四边形ABCD的边AB和AD上分别取点E和F,使AE=AB,AF=AD,连接EF交对角线AC于G,则的值是 .
10.如图,在 ABCD中,E为CD上一点,连接AE,BD交于点F,S△DEF:S△ABF=4:25,则DE:EC= .
11.已知:如图, 、 是⊙ 的割线, , , .则 = .
12.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为 cm.
13.如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是 .
三、解答题
14.如图,四边形 是平行四边形,E是 延长线上的一点,连接 交 于点F.求证: .
15.如图,在边长为1的正方形网格内有一个三角形ABC
(1)把△ABC沿着轴向右平移5个单位得到△A1B1C1,请你画出△A1B1C1
(2)请你以O点为位似中心在第一象限内画出△ABC的位似图形△A2B2C2,使得△ABC与△A2B2C2的位似比为1:2;
(3)请你写出△A2B2C2三个顶点的坐标。(3分)
16.如图,四边形中ABCD中,E,F分别是AB,CD的中点,P为对角线AC延长线上的任意一点,PF交AD于M,PE交BC于N,EF交MN于K.
求证:K是线段MN的中点.
17.如图,矩形ABCD,BF⊥AC交CD于点E,交AD的延长线于点F.
(1)求证:AB2=BC·AF.
(2)当=,DF=5时,求AC的长.
18.如图, 是 的直径,点D在半径 上(D与O、A不重合), ,且 .连接 ,与 交于点F,在 上取一点E,使 .
(1)求证: 是 的切线;
(2)若D是 的中点, ,求 的长.
参考答案
1.B
2.D
3.B
4.B
5.C
6.B
7.A
8.C
9.
10.2:3
11.8
12.18
13.(1,)或(,)
14.证明:∵四边形 是平行四边形
∴ ,
∴
在 和 中
∵ ,
∴ .
15.解;(1)如图所示,△A1B1C1为所求的三角形;
(2)如图所示,△A2B2C2为所求的三角形;
(3)根据图形得:A2(6,0),B2(6,4),C2(2,6).
16.证明:∵EF截△PMN,
则(1)
∵BC截△PAE,
则(2),
∴即有,
所以(3),
∵CD截△PMA,
则,
即,∴(4)
因AP=AC+CP,得2CP+AC=2AP﹣AC,由(3),(4)得,
,
即 ,
所以由(1)得NK=KM,即K是线段MN的中点.
17.(1)证明:∵矩形ABCD
∴∠FAB=∠ABC=90°
∵BF⊥AC
∴∠ACB+∠CBE=∠CBE+∠FBA=90°
∴∠ACB=∠FBA
∴△ABF∽△BCA
∴
∴
(2)解:∵
∴设BC=2x,AB=3x
∵
∴
∴
∴BC=4, AB=6
∴
18.(1)证明:如图,连接 ,
∵ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∵ 为 的半径,
∴ 是 的切线;
(2)解:连接 ,如图,
∵ 是 的直径,
∴ ,
∵D是 的中点,
∴ ,
∴ ,
∵ , ,
∴ ,由勾股定理得: ,
∵ , ,
∴ ,
∴ ,
∴ ,
∴
同课章节目录
