2024年九年级中考数学一轮复习考点突破练习-与圆有关的位置关系(含答案)
文档属性
| 名称 | 2024年九年级中考数学一轮复习考点突破练习-与圆有关的位置关系(含答案) | 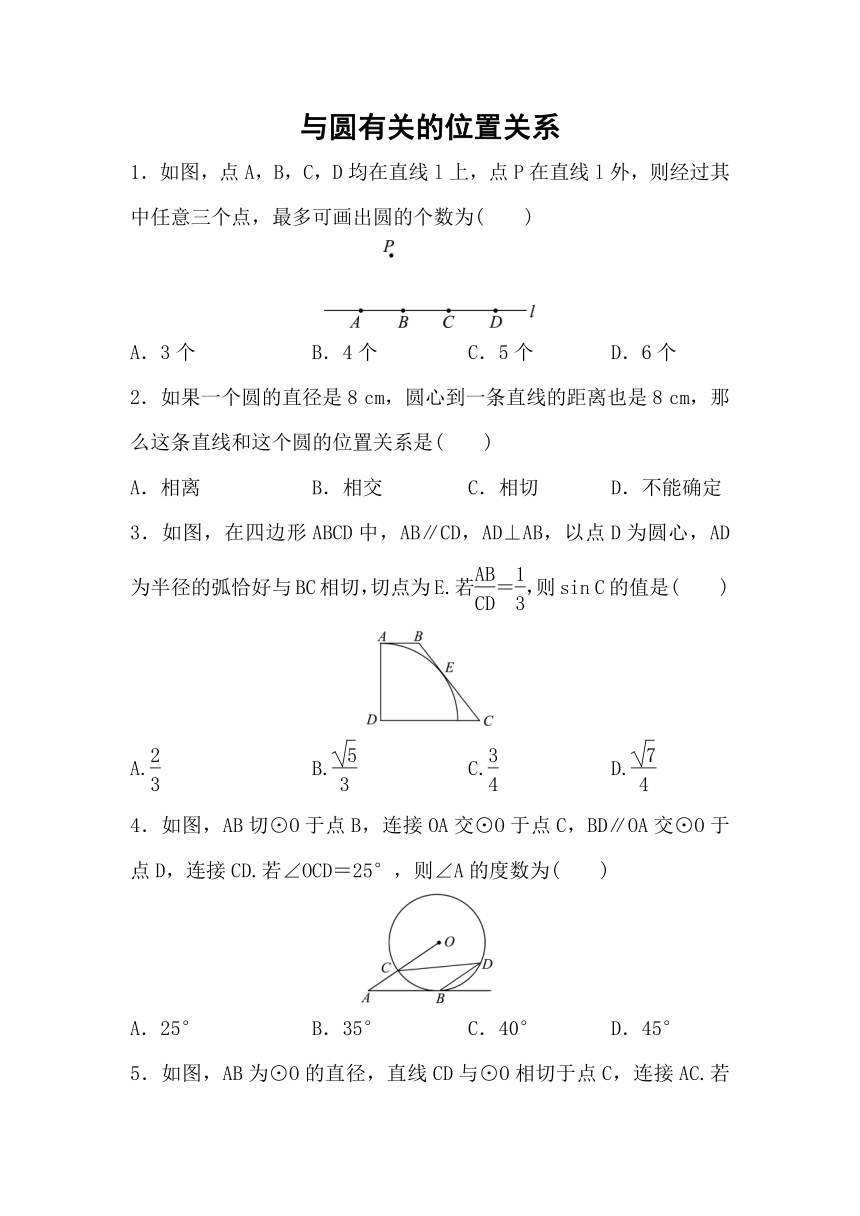 | |
| 格式 | docx | ||
| 文件大小 | 695.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 10:41:11 | ||
图片预览




文档简介
与圆有关的位置关系
1.如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为( )
A.3个 B.4个 C.5个 D.6个
2.如果一个圆的直径是8 cm,圆心到一条直线的距离也是8 cm,那么这条直线和这个圆的位置关系是( )
A.相离 B.相交 C.相切 D.不能确定
3.如图,在四边形ABCD中,AB∥CD,AD⊥AB,以点D为圆心,AD为半径的弧恰好与BC相切,切点为E.若=,则sin C的值是( )
A. B. C. D.
4.如图,AB切⊙O于点B,连接OA交⊙O于点C,BD∥OA交⊙O于点D,连接CD.若∠OCD=25°,则∠A的度数为( )
A.25° B.35° C.40° D.45°
5.如图,AB为⊙O的直径,直线CD与⊙O相切于点C,连接AC.若∠ACD=50°,则∠BAC的度数为( )
A.30° B.40° C.50° D.60°
6.在△ABC中,BC=3,AC=4,下列说法错误的是( )
A.1C.△ABC内切圆的半径r<1 D.当AB=时,△ABC是直角三角形
7.如图,点O是△ABC外接圆的圆心,点I是△ABC的内心,连接OB,IA.若∠CAI=35°,则∠OBC的度数为( )
A.15° B.17.5° C.20° D.25°
8.如图,在Rt△ABC中,∠C=90°,点D在斜边AB上,以AD为直径的半圆O与BC相切于点E,与AC相交于点F,连接DE.若AC=8,BC=6,则DE的长是( )
A. B. C. D.
9.如图,在平面直角坐标系xOy中,直线y=-x-2与x轴、y轴分别交于A,B两点,C,D是半径为1的⊙O上两动点,且CD=,点P为弦CD的中点.当C,D两点在圆上运动时,△PAB面积的最大值是( )
A.8 B.6 C.4 D.3
10.为了测量一个圆形光盘的半径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=4cm,则这张光盘的半径是______cm.(精确到 0.1 cm.参考数据:≈1.73)
11.如图,PA,PB是⊙O的切线,点A,B为切点,∠OAB=38°,则∠P=________°.
12.如图,在⊙O中,直径AB与弦CD交于点E. =2,连接AD,过点B的切线与AD的延长线交于点F.若∠AFB=68°,则∠DEB=________°.
13.如图,在△ABC中,∠ACB=90°,D是AB上一点,且∠BCD=∠A,点O在BC上,以点O为圆心的圆经过C,D两点.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若sin B=,⊙O的半径为3,求AC的长.
14.如图,在△ABC中,∠ACB=70°,△ABC的内切圆⊙O与AB,BC分别相切于点D,E,连接DE,AO的延长线交DE于点F,则∠AFD=________.
15.如图,已知AB是⊙O的直径,直线DC是⊙O的切线,切点为C,AE⊥DC,垂足为E.连接AC.
(1)求证:AC平分∠BAE;
(2)若AC=5,tan∠ACE=,求⊙O的半径.
16.筒车是我国古代利用水力驱动的灌溉工具,车轮缚以竹筒,旋转时低则舀水,高则泻水.如图,水力驱动筒车按逆时针方向转动,竹筒把水引至A处,水沿射线AD方向泻至水渠DE,水渠DE所在直线与水面PQ平行.设筒车为⊙O,⊙O与直线PQ交于P,Q两点,与直线DE交于B,C两点,恰有AD2=BD·CD,连接AB,AC.
(1)求证:AD为⊙O的切线;
(2)筒车的半径为3 m,AC=BC,∠C=30°.当水面上升,A,O,Q三点恰好共线时,求筒车在水面下的最大深度.(精确到0.1 m.参考数据:≈1.4,≈1.7)
1.D 2.A 3.B 4.C 5.B 6.C 7.C 8.B 9.D
10.6.9
11.76
12.66
13.解:(1)直线AB与⊙O相切.
理由如下:如图,连接OD.
∵OC=OD,
∴∠OCD=∠ODC,
∴∠DOB=∠OCD+∠ODC=2∠BCD,
∴∠BCD=∠BOD.
∵∠BCD=∠A,
∴∠BOD=∠A.
∵∠ACB=90°,∴∠A+∠B=90°,
∴∠BOD+∠B=90°,∴∠BDO=90°.
∵OD是⊙O的半径,∴直线AB与⊙O相切.
(2)∵sin B==,OD=3,
∴OB=5,∴BC=OB+OC=8.
在Rt△ACB中,sin B==,
∴设AC=3x,AB=5x,
∴BC==4x=8,
∴x=2,∴AC=3x=6.
14.35°
15.(1)证明:如图,连接OC.
∵直线DC是⊙O的切线,切点为C,∴OC⊥DC.
又∵AE⊥DC,∴OC∥AE,
∴∠EAC=∠ACO.
∵OC=OA,∴∠ACO=∠OAC,
∴∠EAC=∠OAC,
∴AC平分∠BAE.
(2)解:如图,连接BC.
∵AB是⊙O的直径,
∴∠ACB=90°.
又∵AE⊥DC,
由(1)得∠EAC=∠OAC,
∴∠ABC=∠ACE,
∴tan∠ABC=tan∠ACE=,
∴==,∴BC=.
在Rt△ABC中,AB==,
∴OA=.
16.(1)证明:如图,连接AO,并延长交⊙O于点G,连接BG,
∴∠ACB=∠AGB.
∵AG是直径,∴∠ABG=90°,∴∠BAG+∠AGB=90°.
∵AD2=BD·CD,∴=.
∵∠ADB=∠CDA,∴△DAB∽△DCA,
∴∠DAB=∠ACB,∴∠DAB=∠AGB,
∴∠DAB+∠BAG=90°,∴AD⊥AO.
又∵OA是⊙O的半径,∴AD为⊙O的切线.
(2)解:如图,当水面到KH时,A,O,Q三点共线,过点M作OM⊥KH于点M.
∵CA=CB,∠C=30°,∴∠AKB=30°,∠ABC=75°.
∵AK是直径,∴∠ABK=90°,∴∠CBK=15°.
∵BC∥KH,∴∠BKH=∠CBK=15°,
∴∠AKM=∠AKB+∠BKH=45°,∴OM=OK=,
∴筒车在水面下的最大深度为3-≈0.9(m).
1.如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为( )
A.3个 B.4个 C.5个 D.6个
2.如果一个圆的直径是8 cm,圆心到一条直线的距离也是8 cm,那么这条直线和这个圆的位置关系是( )
A.相离 B.相交 C.相切 D.不能确定
3.如图,在四边形ABCD中,AB∥CD,AD⊥AB,以点D为圆心,AD为半径的弧恰好与BC相切,切点为E.若=,则sin C的值是( )
A. B. C. D.
4.如图,AB切⊙O于点B,连接OA交⊙O于点C,BD∥OA交⊙O于点D,连接CD.若∠OCD=25°,则∠A的度数为( )
A.25° B.35° C.40° D.45°
5.如图,AB为⊙O的直径,直线CD与⊙O相切于点C,连接AC.若∠ACD=50°,则∠BAC的度数为( )
A.30° B.40° C.50° D.60°
6.在△ABC中,BC=3,AC=4,下列说法错误的是( )
A.1
7.如图,点O是△ABC外接圆的圆心,点I是△ABC的内心,连接OB,IA.若∠CAI=35°,则∠OBC的度数为( )
A.15° B.17.5° C.20° D.25°
8.如图,在Rt△ABC中,∠C=90°,点D在斜边AB上,以AD为直径的半圆O与BC相切于点E,与AC相交于点F,连接DE.若AC=8,BC=6,则DE的长是( )
A. B. C. D.
9.如图,在平面直角坐标系xOy中,直线y=-x-2与x轴、y轴分别交于A,B两点,C,D是半径为1的⊙O上两动点,且CD=,点P为弦CD的中点.当C,D两点在圆上运动时,△PAB面积的最大值是( )
A.8 B.6 C.4 D.3
10.为了测量一个圆形光盘的半径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=4cm,则这张光盘的半径是______cm.(精确到 0.1 cm.参考数据:≈1.73)
11.如图,PA,PB是⊙O的切线,点A,B为切点,∠OAB=38°,则∠P=________°.
12.如图,在⊙O中,直径AB与弦CD交于点E. =2,连接AD,过点B的切线与AD的延长线交于点F.若∠AFB=68°,则∠DEB=________°.
13.如图,在△ABC中,∠ACB=90°,D是AB上一点,且∠BCD=∠A,点O在BC上,以点O为圆心的圆经过C,D两点.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若sin B=,⊙O的半径为3,求AC的长.
14.如图,在△ABC中,∠ACB=70°,△ABC的内切圆⊙O与AB,BC分别相切于点D,E,连接DE,AO的延长线交DE于点F,则∠AFD=________.
15.如图,已知AB是⊙O的直径,直线DC是⊙O的切线,切点为C,AE⊥DC,垂足为E.连接AC.
(1)求证:AC平分∠BAE;
(2)若AC=5,tan∠ACE=,求⊙O的半径.
16.筒车是我国古代利用水力驱动的灌溉工具,车轮缚以竹筒,旋转时低则舀水,高则泻水.如图,水力驱动筒车按逆时针方向转动,竹筒把水引至A处,水沿射线AD方向泻至水渠DE,水渠DE所在直线与水面PQ平行.设筒车为⊙O,⊙O与直线PQ交于P,Q两点,与直线DE交于B,C两点,恰有AD2=BD·CD,连接AB,AC.
(1)求证:AD为⊙O的切线;
(2)筒车的半径为3 m,AC=BC,∠C=30°.当水面上升,A,O,Q三点恰好共线时,求筒车在水面下的最大深度.(精确到0.1 m.参考数据:≈1.4,≈1.7)
1.D 2.A 3.B 4.C 5.B 6.C 7.C 8.B 9.D
10.6.9
11.76
12.66
13.解:(1)直线AB与⊙O相切.
理由如下:如图,连接OD.
∵OC=OD,
∴∠OCD=∠ODC,
∴∠DOB=∠OCD+∠ODC=2∠BCD,
∴∠BCD=∠BOD.
∵∠BCD=∠A,
∴∠BOD=∠A.
∵∠ACB=90°,∴∠A+∠B=90°,
∴∠BOD+∠B=90°,∴∠BDO=90°.
∵OD是⊙O的半径,∴直线AB与⊙O相切.
(2)∵sin B==,OD=3,
∴OB=5,∴BC=OB+OC=8.
在Rt△ACB中,sin B==,
∴设AC=3x,AB=5x,
∴BC==4x=8,
∴x=2,∴AC=3x=6.
14.35°
15.(1)证明:如图,连接OC.
∵直线DC是⊙O的切线,切点为C,∴OC⊥DC.
又∵AE⊥DC,∴OC∥AE,
∴∠EAC=∠ACO.
∵OC=OA,∴∠ACO=∠OAC,
∴∠EAC=∠OAC,
∴AC平分∠BAE.
(2)解:如图,连接BC.
∵AB是⊙O的直径,
∴∠ACB=90°.
又∵AE⊥DC,
由(1)得∠EAC=∠OAC,
∴∠ABC=∠ACE,
∴tan∠ABC=tan∠ACE=,
∴==,∴BC=.
在Rt△ABC中,AB==,
∴OA=.
16.(1)证明:如图,连接AO,并延长交⊙O于点G,连接BG,
∴∠ACB=∠AGB.
∵AG是直径,∴∠ABG=90°,∴∠BAG+∠AGB=90°.
∵AD2=BD·CD,∴=.
∵∠ADB=∠CDA,∴△DAB∽△DCA,
∴∠DAB=∠ACB,∴∠DAB=∠AGB,
∴∠DAB+∠BAG=90°,∴AD⊥AO.
又∵OA是⊙O的半径,∴AD为⊙O的切线.
(2)解:如图,当水面到KH时,A,O,Q三点共线,过点M作OM⊥KH于点M.
∵CA=CB,∠C=30°,∴∠AKB=30°,∠ABC=75°.
∵AK是直径,∴∠ABK=90°,∴∠CBK=15°.
∵BC∥KH,∴∠BKH=∠CBK=15°,
∴∠AKM=∠AKB+∠BKH=45°,∴OM=OK=,
∴筒车在水面下的最大深度为3-≈0.9(m).
同课章节目录
