2024年鲁教版(五四制)中考数学一轮复习 一次函数专题复习---一次函数存在性问题之—次函数存在性之等腰三角形(无答案)
文档属性
| 名称 | 2024年鲁教版(五四制)中考数学一轮复习 一次函数专题复习---一次函数存在性问题之—次函数存在性之等腰三角形(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 179.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 11:12:10 | ||
图片预览


文档简介
鲁教版2023-2024一次函数专题复习---一次函数存在性问题之—次函数存在性之等腰三角形
知识点精讲
1.存在性问题:通常是在变化的过程中,根据已知条件,探索某种状态是否存在的题目,主要考查运动的结果.
2.存在性问题处理框架:
①研究背景图形.
②分析不变特征,确定分类标准.
③分析特殊状态的形成因素,画出符合题意的图形并求解.
④结果验证.
3.不变特征举例:
①等腰三角形
以定线段作为底边或者腰确定分类标准,利用两圆一线确定点的位置.
两个定点一动点构成等腰三角形的策略
方法一
①首先弄清题中是否规定了哪个点为等腰三角形的顶点.(若某边底,则只有一种情况;若某边为腰,有两种情况;若只说该三点构成等腰三角形,则有三种情况),先借助于动点所在图象的解析式,表示出动点的坐标(标横表纵),按分类的情况,分别利用相应类别下两腰相等,使用两点间的距离公式,建立方程.
解出此方程,即可求出动点的横坐标,再借助动点所在图象的函数关系式,可求出动点纵坐标,注意去掉不合题意的点(就是不能构成三角形这个题意).
方法二
①(两圆一线)或(两圆一垂)当定长为腰,找已知直线上满足条件的点时,以定长的某一端点为圆心,以定长为半径画弧,若所画弧与已知直线有交点且交点不是定长的另一端点时,交点即为所求的点,若所画弧与已知直线无交点或交点是定长的另一端点时,满足条件的点不存在,②当定长为底边时,作出定长的垂直平分线,若作出的垂直平分线与已知直线有交点,则交点即为所求的点,若作出的垂直平分线与已知直线无交点,则满足条件的点不存在,用以上方法即可找出所有符合条件的点.
特殊
①y=x+b与x轴所夹的锐角为45°;②y=±x+b与x轴所夹的锐角为60°;③y=±x+b与x轴所夹的锐角为30°.
注意:函数与坐标轴夹角为特殊角要进行简单的过程书写,不可以直接用.函数是一个工具,将几何与函数有机的结合,特殊三角形角的边长关系:
30°,60°,90°的直角三角形比例为1:2:.
120°的等腰三角形比例为1:1: .
45°,45°,90°比例为1:1:.
1. 如图,以矩形的相邻边建立直角坐标系,.点是边上一点,将沿着翻折,点恰好落在边上,记为.
求折痕所在直线的函数解析式;
若把翻折后的矩形沿轴正半轴向上平移个单位,连结,若是等腰三角形,求的值
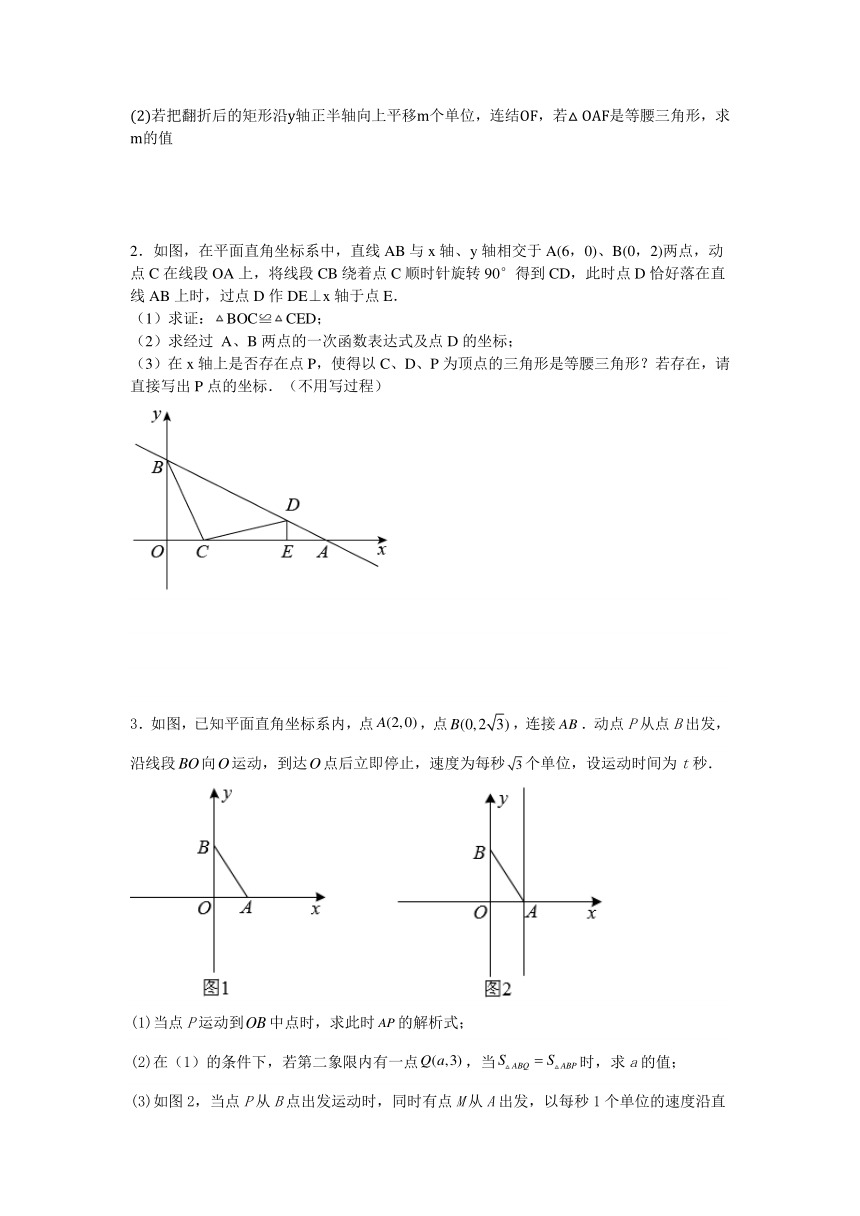
2.如图,在平面直角坐标系中,直线AB与x轴、y轴相交于A(6,0)、B(0,2)两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.
(1)求证:BOC≌CED;
(2)求经过 A、B两点的一次函数表达式及点D的坐标;
(3)在x轴上是否存在点P,使得以C、D、P为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标.(不用写过程)
3.如图,已知平面直角坐标系内,点,点,连接.动点P从点B出发,沿线段向运动,到达点后立即停止,速度为每秒个单位,设运动时间为t秒.
(1)当点P运动到中点时,求此时的解析式;
(2)在(1)的条件下,若第二象限内有一点,当时,求a的值;
(3)如图2,当点P从B点出发运动时,同时有点M从A出发,以每秒1个单位的速度沿直线向上运动,点P停止运动,点M也立即停止运动.过点P作轴交于点N.在运动过程中,是否存在t,使得为等腰三角形?若存在,求出此时的t值,若不存在,说明理由.
4如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B.与直线y=x相交于点A.
(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(3)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
5.如图,在平面直角坐标系中,一次函数y=﹣x+6的图象与x轴、y轴分别交于B、C两点,与正比例函数的图象交于点A.
(1)求A、B、C三点的坐标;
(2)若动点M在线段AC上运动,当OMC的面积是OAC的面积的时,求出此时点M的坐标.
(3)在y轴上是否存在点N,使NAC为等腰三角形,若存在,直接写出点N的坐标;若不存在.请说明理由.
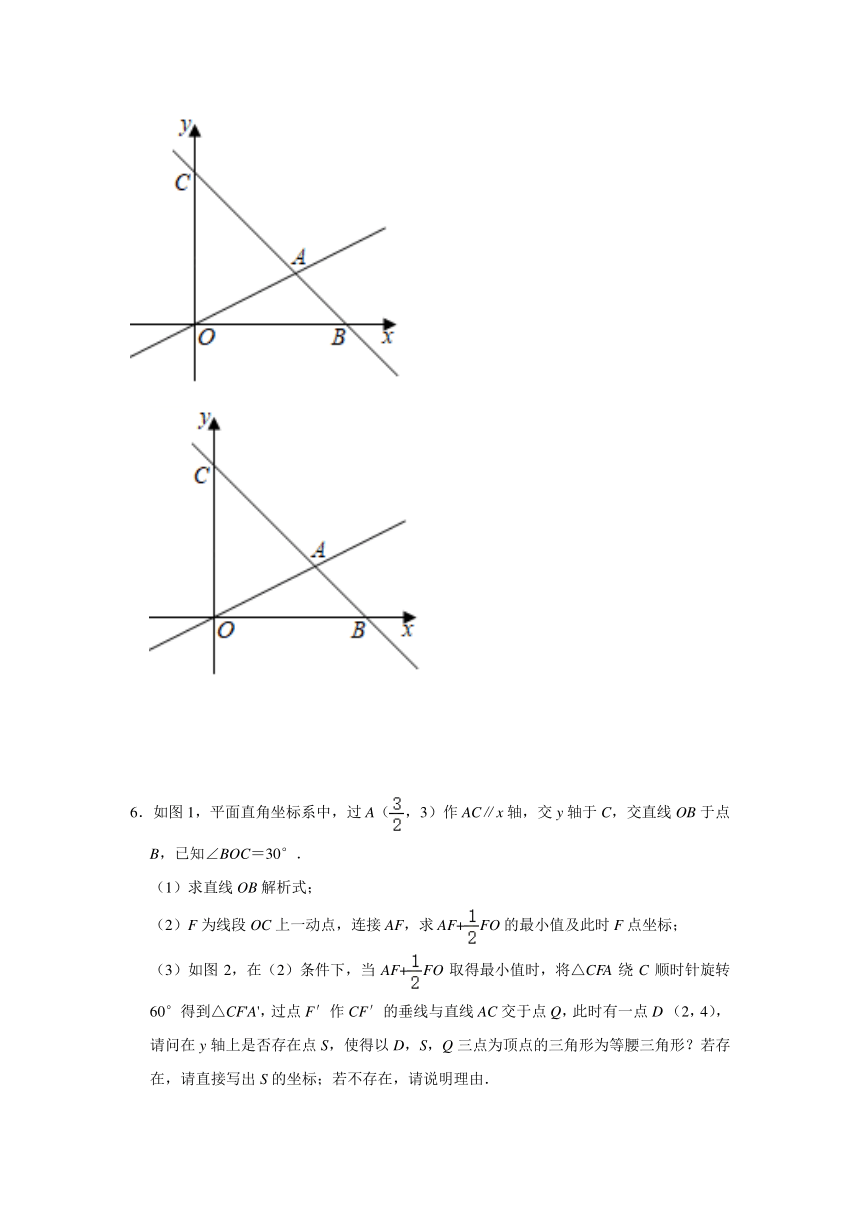
6.如图1,平面直角坐标系中,过A(,3)作AC∥x轴,交y轴于C,交直线OB于点B,已知∠BOC=30°.
(1)求直线OB解析式;
(2)F为线段OC上一动点,连接AF,求AF+FO的最小值及此时F点坐标;
(3)如图2,在(2)条件下,当AF+FO取得最小值时,将△CFA绕C顺时针旋转60°得到△CF'A',过点F′作CF′的垂线与直线AC交于点Q,此时有一点D (2,4),请问在y轴上是否存在点S,使得以D,S,Q三点为顶点的三角形为等腰三角形?若存在,请直接写出S的坐标;若不存在,请说明理由.
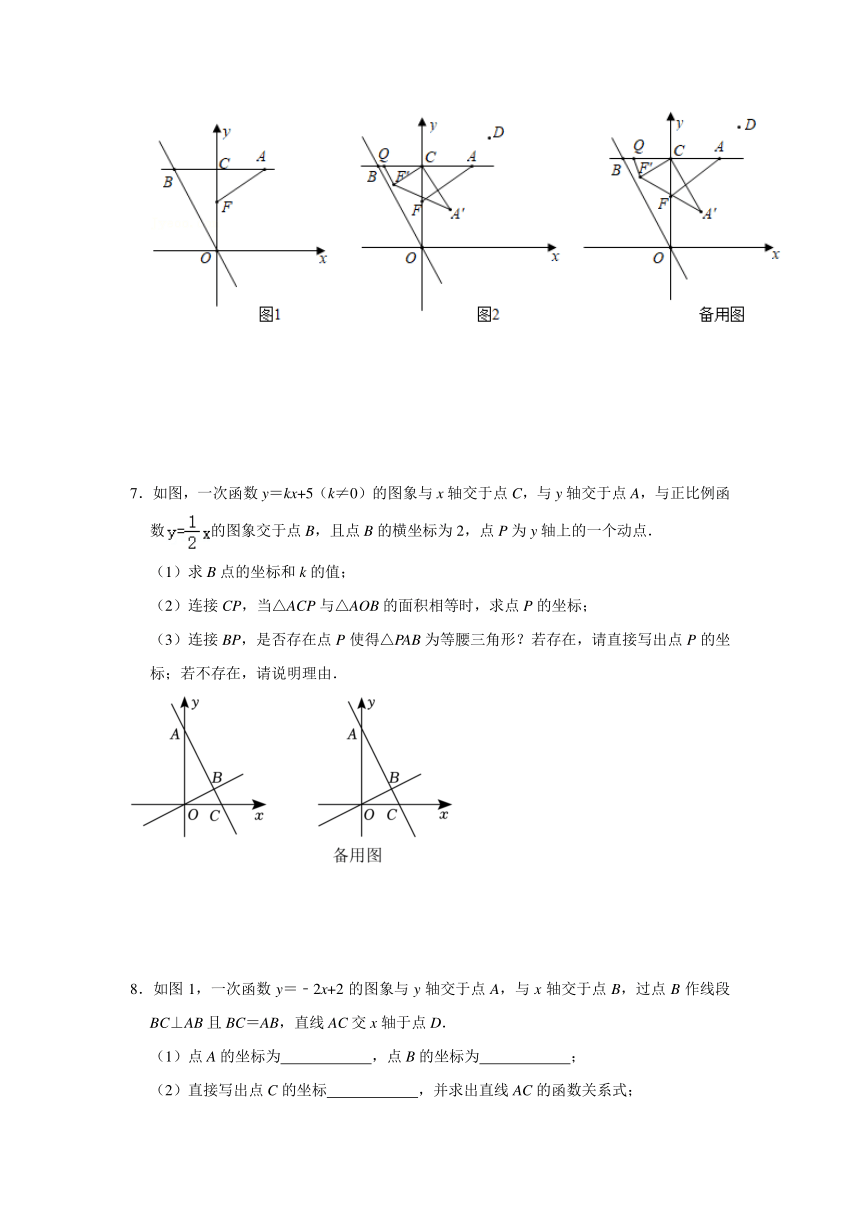
7.如图,一次函数y=kx+5(k≠0)的图象与x轴交于点C,与y轴交于点A,与正比例函数的图象交于点B,且点B的横坐标为2,点P为y轴上的一个动点.
(1)求B点的坐标和k的值;
(2)连接CP,当△ACP与△AOB的面积相等时,求点P的坐标;
(3)连接BP,是否存在点P使得△PAB为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
8.如图1,一次函数y=﹣2x+2的图象与y轴交于点A,与x轴交于点B,过点B作线段BC⊥AB且BC=AB,直线AC交x轴于点D.
(1)点A的坐标为 ,点B的坐标为 ;
(2)直接写出点C的坐标 ,并求出直线AC的函数关系式;
(3)若点P是图1中直线AC上的一点,连接OP,得到图2.当点P在第二象限,且到x轴,y轴的距离相等时,直接写出△AOP的面积;
(4)若点Q是图1中坐标平面内不同于点B、点C的一点,当以点C,D,Q为顶点的三角形与△BCD全等时,直接写出点Q的坐标.
9综合与探究:
如图,在平面直角坐标系中,一次函数的图象分别交x、y轴于点A、B,点C在y轴上,AC平分∠OAB.
(1)求点A、B的坐标;
(2)求线段BC的长;
(3)在平面直角坐标系中是否存在点D,使得△ABD是以AB为直角边的等腰直角三角形,若存在,请直接写出点D的坐标,若不存在,请说明理由.
10.如图,直线与x轴交于点A,与y轴交于点B,直线l2与x轴交于点C,与y轴交于D点,AC=8,OD=3OC.
(1)求直线CD的解析式;
(2)点Q为直线AB上一动点,若有,请求出Q点坐标;
(3)点M为直线AB上一动点,点N为y轴上一动点,是否存在以点M,N,C为顶点且以MN为直角边的三角形是等腰直角三角形,若存在,请直接写出点M的坐标,并写出其中一个点M的求解过程,若不存在,请说明理由.
11.如图,在平面直角坐标系中,直线y=x+3与x轴,y轴分别交于点A,C,经过点C的直线与x轴交于点B(3,0).
(1)求直线BC的解析式;
(2)点G是线段BC上一动点,若直线AG把△ABC的面积分成2:1的两部分,请求点G的坐标;
(3)已知D为AC的中点,点P是平面内一点,当△CDP是以CD为直角边的等腰直角三角形时,直接写出点P的坐标.
知识点精讲
1.存在性问题:通常是在变化的过程中,根据已知条件,探索某种状态是否存在的题目,主要考查运动的结果.
2.存在性问题处理框架:
①研究背景图形.
②分析不变特征,确定分类标准.
③分析特殊状态的形成因素,画出符合题意的图形并求解.
④结果验证.
3.不变特征举例:
①等腰三角形
以定线段作为底边或者腰确定分类标准,利用两圆一线确定点的位置.
两个定点一动点构成等腰三角形的策略
方法一
①首先弄清题中是否规定了哪个点为等腰三角形的顶点.(若某边底,则只有一种情况;若某边为腰,有两种情况;若只说该三点构成等腰三角形,则有三种情况),先借助于动点所在图象的解析式,表示出动点的坐标(标横表纵),按分类的情况,分别利用相应类别下两腰相等,使用两点间的距离公式,建立方程.
解出此方程,即可求出动点的横坐标,再借助动点所在图象的函数关系式,可求出动点纵坐标,注意去掉不合题意的点(就是不能构成三角形这个题意).
方法二
①(两圆一线)或(两圆一垂)当定长为腰,找已知直线上满足条件的点时,以定长的某一端点为圆心,以定长为半径画弧,若所画弧与已知直线有交点且交点不是定长的另一端点时,交点即为所求的点,若所画弧与已知直线无交点或交点是定长的另一端点时,满足条件的点不存在,②当定长为底边时,作出定长的垂直平分线,若作出的垂直平分线与已知直线有交点,则交点即为所求的点,若作出的垂直平分线与已知直线无交点,则满足条件的点不存在,用以上方法即可找出所有符合条件的点.
特殊
①y=x+b与x轴所夹的锐角为45°;②y=±x+b与x轴所夹的锐角为60°;③y=±x+b与x轴所夹的锐角为30°.
注意:函数与坐标轴夹角为特殊角要进行简单的过程书写,不可以直接用.函数是一个工具,将几何与函数有机的结合,特殊三角形角的边长关系:
30°,60°,90°的直角三角形比例为1:2:.
120°的等腰三角形比例为1:1: .
45°,45°,90°比例为1:1:.
1. 如图,以矩形的相邻边建立直角坐标系,.点是边上一点,将沿着翻折,点恰好落在边上,记为.
求折痕所在直线的函数解析式;
若把翻折后的矩形沿轴正半轴向上平移个单位,连结,若是等腰三角形,求的值
2.如图,在平面直角坐标系中,直线AB与x轴、y轴相交于A(6,0)、B(0,2)两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.
(1)求证:BOC≌CED;
(2)求经过 A、B两点的一次函数表达式及点D的坐标;
(3)在x轴上是否存在点P,使得以C、D、P为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标.(不用写过程)
3.如图,已知平面直角坐标系内,点,点,连接.动点P从点B出发,沿线段向运动,到达点后立即停止,速度为每秒个单位,设运动时间为t秒.
(1)当点P运动到中点时,求此时的解析式;
(2)在(1)的条件下,若第二象限内有一点,当时,求a的值;
(3)如图2,当点P从B点出发运动时,同时有点M从A出发,以每秒1个单位的速度沿直线向上运动,点P停止运动,点M也立即停止运动.过点P作轴交于点N.在运动过程中,是否存在t,使得为等腰三角形?若存在,求出此时的t值,若不存在,说明理由.
4如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B.与直线y=x相交于点A.
(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(3)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
5.如图,在平面直角坐标系中,一次函数y=﹣x+6的图象与x轴、y轴分别交于B、C两点,与正比例函数的图象交于点A.
(1)求A、B、C三点的坐标;
(2)若动点M在线段AC上运动,当OMC的面积是OAC的面积的时,求出此时点M的坐标.
(3)在y轴上是否存在点N,使NAC为等腰三角形,若存在,直接写出点N的坐标;若不存在.请说明理由.
6.如图1,平面直角坐标系中,过A(,3)作AC∥x轴,交y轴于C,交直线OB于点B,已知∠BOC=30°.
(1)求直线OB解析式;
(2)F为线段OC上一动点,连接AF,求AF+FO的最小值及此时F点坐标;
(3)如图2,在(2)条件下,当AF+FO取得最小值时,将△CFA绕C顺时针旋转60°得到△CF'A',过点F′作CF′的垂线与直线AC交于点Q,此时有一点D (2,4),请问在y轴上是否存在点S,使得以D,S,Q三点为顶点的三角形为等腰三角形?若存在,请直接写出S的坐标;若不存在,请说明理由.
7.如图,一次函数y=kx+5(k≠0)的图象与x轴交于点C,与y轴交于点A,与正比例函数的图象交于点B,且点B的横坐标为2,点P为y轴上的一个动点.
(1)求B点的坐标和k的值;
(2)连接CP,当△ACP与△AOB的面积相等时,求点P的坐标;
(3)连接BP,是否存在点P使得△PAB为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
8.如图1,一次函数y=﹣2x+2的图象与y轴交于点A,与x轴交于点B,过点B作线段BC⊥AB且BC=AB,直线AC交x轴于点D.
(1)点A的坐标为 ,点B的坐标为 ;
(2)直接写出点C的坐标 ,并求出直线AC的函数关系式;
(3)若点P是图1中直线AC上的一点,连接OP,得到图2.当点P在第二象限,且到x轴,y轴的距离相等时,直接写出△AOP的面积;
(4)若点Q是图1中坐标平面内不同于点B、点C的一点,当以点C,D,Q为顶点的三角形与△BCD全等时,直接写出点Q的坐标.
9综合与探究:
如图,在平面直角坐标系中,一次函数的图象分别交x、y轴于点A、B,点C在y轴上,AC平分∠OAB.
(1)求点A、B的坐标;
(2)求线段BC的长;
(3)在平面直角坐标系中是否存在点D,使得△ABD是以AB为直角边的等腰直角三角形,若存在,请直接写出点D的坐标,若不存在,请说明理由.
10.如图,直线与x轴交于点A,与y轴交于点B,直线l2与x轴交于点C,与y轴交于D点,AC=8,OD=3OC.
(1)求直线CD的解析式;
(2)点Q为直线AB上一动点,若有,请求出Q点坐标;
(3)点M为直线AB上一动点,点N为y轴上一动点,是否存在以点M,N,C为顶点且以MN为直角边的三角形是等腰直角三角形,若存在,请直接写出点M的坐标,并写出其中一个点M的求解过程,若不存在,请说明理由.
11.如图,在平面直角坐标系中,直线y=x+3与x轴,y轴分别交于点A,C,经过点C的直线与x轴交于点B(3,0).
(1)求直线BC的解析式;
(2)点G是线段BC上一动点,若直线AG把△ABC的面积分成2:1的两部分,请求点G的坐标;
(3)已知D为AC的中点,点P是平面内一点,当△CDP是以CD为直角边的等腰直角三角形时,直接写出点P的坐标.
同课章节目录
