2024年九年级中考数学选择题填空题练习(无答案)
文档属性
| 名称 | 2024年九年级中考数学选择题填空题练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 10:50:32 | ||
图片预览



文档简介
题组特训 一
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. 下列4个实数中,为无理数的是( )
A. - B. C. D. 3.14
2. 下列分别是山东、重庆、江苏、甘肃电视台的标志,其中是中心对称图形但不是轴对称图形的是( )
3. 下列运算结果是m8的是( )
A. m2·m4 B. (m4)2
C. m4+m4 D. m16÷m2
4. 如图是由一个长方体和一个圆锥组成的几何体,则它的俯视图是( )
5. 若正多边形的一个外角是72°,则该正多边形的内角和为( )
A. 900° B. 720°
C. 540° D. 360°
6. 在某市组织的物理实验操作考试中,考试所用实验室共有24个测试位,分成6组,同组4个测试位各有一道相同试题,各组的试题不同,分别标记为A,B,C,D,E,F,考生从中随机抽取一道试题,则某个考生抽到试题A的概率为( )
A. B. C. D.
7. 如图,在Rt△ABC中,∠C=90°,AF=EF,若∠B=54°,则∠CFE的度数为( )
第7题图
A. 72°
B. 76°
C. 82°
D. 86°
8. 关于x的方程(m-1)2x2+(2m-1)x+1=0没有实数根,则m的取值范围是( )
A. m<且m≠-1 B. m<
C. m> D. m≤且m≠-1
9. 我国南宋数学家杨辉所著的《详解九章算法》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.根据“杨辉三角”请计算(a+b)10的展开式中第三项的系数为( )
第9题图
A. 45 B. 50 C. 55 D. 60
10. 如图,抛物线y=ax2+bx+c的对称轴为直线x=2,下列结论:①abc>0;②4a-c>0;③9a-3b+c<0; ④若点(-0.5,y1), (-2,y2)均在抛物线上,则y1>y2. 其中正确的个数为( )
第10题图
A. 1个 B. 2个
C. 3个 D. 4个
二、填空题(本大题共6个小题,每小题3分,满分18分)
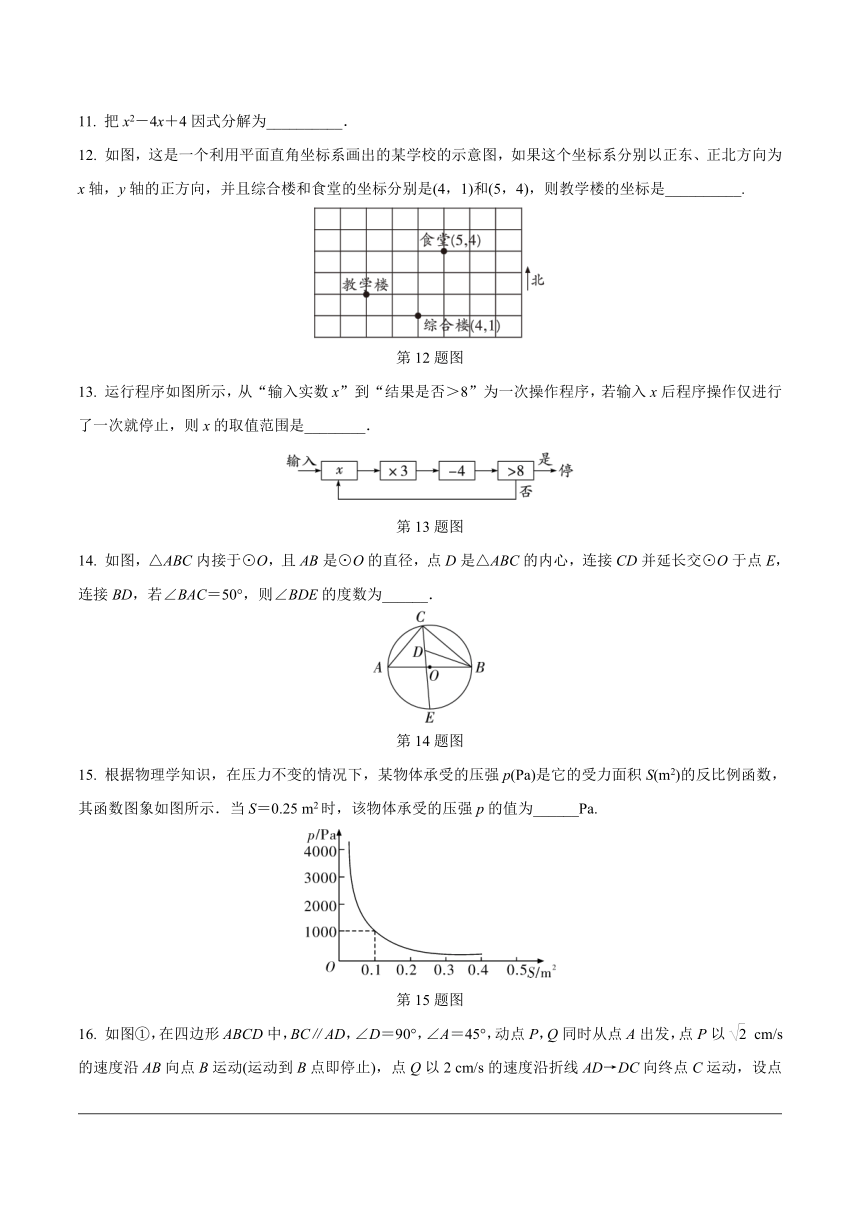
11. 把x2-4x+4因式分解为__________.
12. 如图,这是一个利用平面直角坐标系画出的某学校的示意图,如果这个坐标系分别以正东、正北方向为x轴,y轴的正方向,并且综合楼和食堂的坐标分别是(4,1)和(5,4),则教学楼的坐标是__________.
第12题图
13. 运行程序如图所示,从“输入实数x”到“结果是否>8”为一次操作程序,若输入x后程序操作仅进行了一次就停止,则x的取值范围是________.
第13题图
14. 如图,△ABC内接于⊙O,且AB是⊙O的直径,点D是△ABC的内心,连接CD并延长交⊙O于点E,连接BD,若∠BAC=50°,则∠BDE的度数为______.
第14题图
15. 根据物理学知识,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其函数图象如图所示.当S=0.25 m2时,该物体承受的压强p的值为______Pa.
第15题图
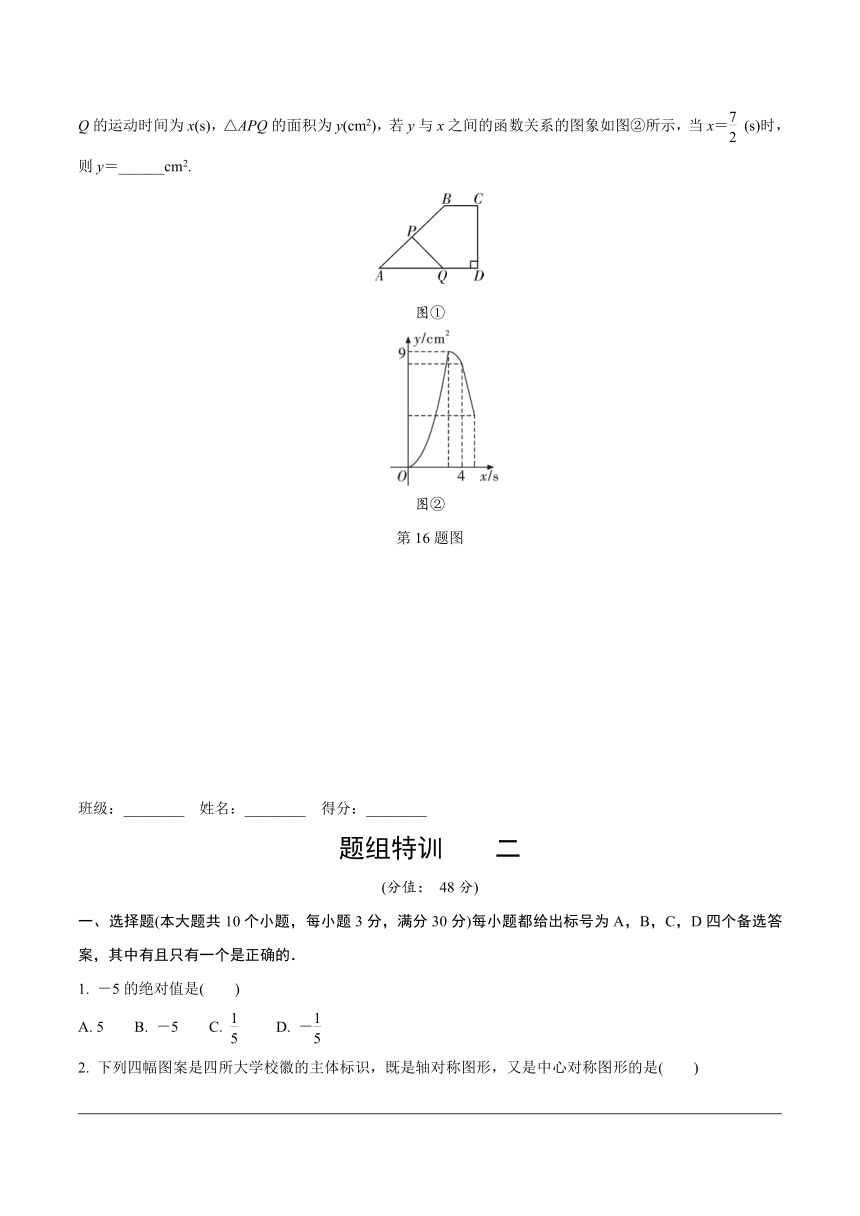
16. 如图①,在四边形ABCD中,BC∥AD,∠D=90°,∠A=45°,动点P,Q同时从点A出发,点P以cm/s的速度沿AB向点B运动(运动到B点即停止),点Q以2 cm/s的速度沿折线AD→DC向终点C运动,设点Q的运动时间为x(s),△APQ的面积为y(cm2),若y与x之间的函数关系的图象如图②所示,当x=(s)时,则y=______cm2.
图①
图②
第16题图
班级:________ 姓名:________ 得分:________
题组特训 二
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. -5的绝对值是( )
A. 5 B. -5 C. D. -
2. 下列四幅图案是四所大学校徽的主体标识,既是轴对称图形,又是中心对称图形的是( )
3. 下列运算正确的是( )
A. 6a2-5a2=1
B. a2·a4=a8
C. (a+b)(a-b)=a2-b2
D. (-3a4)2=-9a8
4. 如图①是由5个完全相同的小正方体组成的立体图形,将上层的小正方体平移后得到图 ②,则关于平移前后几何体的三视图发生改变的是( )
第4题图
A. 主视图
B. 俯视图
C. 左视图
D. 主视图、俯视图和左视图都发生改变
5. 直角三角板如图摆放在两条平行线上,若∠1=21°,则∠2的度数为( )
第5题图
A. 159° B. 146°
C. 114° D. 156°
6. 若用我们数学课本上采用的科学计算器进行计算,其按键顺序及结果如下:
下列判断正确的是( )
A. a>b B. a=b
C. a<b D. 无法确定
7. 函数y=kx+b的图象如图所示,则关于x的一元二次方程x2+kx+b-1=0的根的情况是( )
A. 没有实数根
B. 有两个相等的实数根
C. 有两个不相等的实数根
D. 无法确定
第7题图
8. 如图,在平行四边形ABCD中,E为BC的中点,BD,AE交于点O,若随机向平行四边形ABCD内投一粒米,则米粒落在图中阴影部分的概率为( )
A. B. C. D.
第8题图
9. 已知二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则下列结论中错误的是( )
第9题图
A. bc<0
B. 2a-b>0
C. b2>(a+c)2
D. 点(-3,y1),(1,y2)都在二次函数的图象上,则有y110. 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S11的值为( )
第10题图
A. ()7 B. ()8
C. ()7 D. ()8
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 若代数式在实数范围内有意义,则x的取值范围为________.
12. 《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步. 问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?设有x辆车,人数为y,根据题意可列方程组为______________.
13. 如图,A,B,C,D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=20°,则这个正多边形的边数为________.
第13题图
14. 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图①就是一个幻方.图②是一个未完成的幻方,则x与y的和是__________.
图①
图②
第14题图
15. 如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D是上任意一点,则cos ∠ADC=________.
第15题图
16. 如图①,一张矩形纸片ABCD,点E,F分别在AB,CD上,点G,H分别在AF,EC上,现将该纸片沿AF,GH,EC剪开,拼成如图②所示的矩形,已知DF∶AD=5∶12,GH=6,则AD的长是________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 三
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. -的相反数是( )
A. B. -
C. D. -
2. 下列垃圾分类图标中,其文字上方的图案是轴对称图形,但不是中心对称图形的是( )
3. 如图,在数轴上,点A,B分别表示的数为-4,2,点C是AB的中点,则点C表示的数为( )
第3题图
A. -1 B. 1
C. D. -
4. 如图是由正六棱柱和球体组合而成的几何体,其左视图是( )
5. 一组数据:2,5,5,5,8,若去掉一个数据5,则下列统计量中发生变化的是( )
A. 众数 B. 中位数
C. 平均数 D. 方差
6. 利用科学计算器进行计算,小明的按键顺序为,则计算器显示的结果最接近的一个数是( )
A. 3 B. 4 C. 5 D. 6
7. 如图,某链条每节长为2.8 cm,每两节链条相连接部分重叠的圆的直径为1 cm,按这种连接方式,50节链条总长度为( )
第7题图
A. 81 cm B. 80 cm
C. 91 cm D. 90 cm
8. 如图,在△ABC中,AC=BC,∠A=65°,分别以点B,C为圆心,大于BC的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,连接BD,则∠BDA的度数为( )
第8题图
A. 70° B. 80° C. 90° D. 100°
9. 已知关于x的一元二次方程(m-1)x2-x+1=0有两个不相等的实数根,则m可能的取值为( )
A. 3 B. 4
C. 5 D. 6
10. 如图,正比例函数y1=ax,一次函数y2=mx+n和反比例函数y3=的图象在同一平面直角坐标系中,若y3<y2<y1,则x的取值范围为( )
第10题图
A. x<-3 B. 0<x<1
C. x<-3 或0<x<1 D. -3<x<1
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 据山东省能源局消息,2022年山东省能源行业的发展目标是电力总装机达到180000000千瓦左右.将数据180000000用科学记数法表示为________.
12. 已知最简二次根式与是同类二次根式,那么a的值为________.
13. 两千多年前,古希腊数学家欧多克索斯发现了黄金分割,如图,点P是线段AB上一点(AP>BP),若满足=,则称点P是AB的黄金分割点.黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好. 若舞台长25米,主持人从舞台一侧进入,设他至少走x米时恰好站在舞台的黄金分割点上,则x满足的方程是____________ .
第13题图
14. 如图,在△ABC中,AB=AC=5,BC=6,点D在CA的延长线上,DE⊥BC于点E,若AD=2,则DE的长为________.
第14题图
15. 如图,将△ABC绕点P旋转180°得到△A′B′C′,则点P的坐标为________.
第15题图
16. 二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a>b;③(a+c)2<b2;④a-2b+4c>0,其中正确的是________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 四
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. 9的平方根是( )
A. 3 B. -3 C. ±3 D.
2. 下列由黑白棋子组成的图案中,是轴对称图形的是( )
3. 如图是沿圆柱体顶部圆的直径切去一部分之后所得到的几何体,则该几何体的主视图为( )
4. 2022年3月22日,中央一号文件《中共中央国务院关于做好2022年全面推进乡村振兴重点工作的意见》正式发布.文件中提出,要稳定全年粮食播种面积和产量,确保粮食产量保持在1.3万亿斤以上.将数据1.3万亿用科学记数法表示为 ( )
A. 0.13×1013 B. 1.3×1012
C. 1.3×108 D. 1.3×104
5. 将一枚飞镖任意投掷到如图所示的正六边形镖盘上,飞镖落在阴影区域的概率为 ( )
第5题图
A. B. C. D.
6. 如图,在 ABCD中,过点C作CE⊥BA交BA的延长线于点E,若∠EAD=52°,则∠ECB的度数为( )
第6题图
A. 52° B. 28° C. 38° D. 48°
7. 现有甲、乙、丙三种不同品种糖果的单价与千克数如下表所示:
甲种糖果 乙种糖果 丙种糖果
单价(元/千克) 14 10 8
千克数 2 3 5
将这2千克甲种糖果、3千克乙种糖果和5千克丙种糖果混合成10千克什锦糖果,若商家用加权平均数来确定什锦糖果的单价,则这10千克什锦糖果的单价为( )
A. 9.2 B. 8.9
C. 10 D. 9.8
8. 如图,∠MON=45°,在OM上截取OA1=1.过点A1作A1B1⊥OM,交ON于点B1,以点B1为圆心,B1O为半径画弧,交OM于点A2;过点A2作A2B2⊥OM,交ON于点B2,以点B2为圆心,B2O为半径画弧,交OM于点A3;…;按此规律,所得线段A22B22的长等于( )
第8题图
A. 220 B. 221
C. 222 D. 224
9. 如图,BE是△ABC的中线,点F在BE上,连接AF并延长交BC于点D.若BF=3FE,DC=2,则BD的长为( )
第9题图
A. 6 B. 5
C. 4 D. 3
10. 抛物线y=-x2+mx+n与x轴、y轴分别交于点A(-1,0),B(0,3).下列结论错误的是( )
A. 抛物线的对称轴为直线x=1
B. 抛物线与x轴的另一个交点为(3,0)
C. 方程x2-mx-n=p(p>4)无解
D. 若点(-2,y1)和(5,y2)在抛物线上,则y1>y2
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 把2x2-2因式分解为____________ .
12. 若(a+5)2+|2b-4|=0,则ab=______.
13. 关于x的一元二次方程(a+2)x2-3x+1=0有两个相等的实数根,则a的值为________.
14. 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,若点A的坐标为(0,1),点B坐标为(2,1),则这条圆弧所在圆的圆心坐标为________.
第14题图
15. 如图,在平面直角坐标系xOy中,一次函数y=-x+b的图象分别与x轴、y轴交于点C(4,0),B,与反比例函数y=(x<0)的图象交于点A,连接OA,BC=4AB.则k的值为________.
第15题图
16. 由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为2的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分). 则图中AB的长应是 __________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 五
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. -3的倒数是( )
A. - B. C. -3 D. 3
2. 下列交通标识中,既是轴对称图形,又是中心对称图形的是( )
3. 下列计算结果正确的是( )
A. 5a-3a=2
B. 6a÷2a=3a
C. a6÷a3=a2
D. (2a2b3)3=8a6b9
4. 用四个相同的小正方体搭成几何体,要求每个几何体的主视图、左视图、俯视图中至少有两种视图的形状是相同的,下列四种摆放方式中不符合要求的是( )
5. 将含30°角的三角板ABC和含45°角的三角板DEF按如图所示的位置摆放,AC交DE于点M,若BC∥EF,则∠DMC的度数为( )
第5题图
A. 85° B. 80° C. 75° D. 70°
6. 某学校准备挑选一名学生参加市级演讲比赛,在三轮学校预赛中得到甲、乙、丙、丁四名同学三轮预赛成绩的平均数x和方差s2如下表:
甲 乙 丙 丁
x 95 97 96 97
s2 0.6 1.2 1.2 0.6
根据表中数据,要从甲、乙、丙、丁四名同学中选择一名成绩好又发挥稳定的同学参赛,应该选择( )
A. 甲 B. 乙 C. 丙 D. 丁
7. 下面各图形是由大小相同的三角形摆放而成的,图①中有1个三角形,图②中有5个三角形,图③中有11个三角形,图④中有19个三角形,…,依此规律,则图 中三角形个数是( )
第7题图
A. 155 B. 156 C. 157 D. 144
8. 如图,一次函数y=kx+6(k≠0)的图象经过点A(3,0),与正比例函数y=mx的图象交于点B(a,4),则不等式kx+6>mx的解集为( )
第8题图
A. x<1 B. 1<x<3
C. x>3 D. x<1 或x>3
9. 如图,AC是⊙O的直径,弦BD⊥AC于点G,连接BC,CD,若OG=BD,则∠BCD的大小为( )
第9题图
A. 115° B. 125°
C. 135° D. 150°
10. 如图,在矩形ABCD中,AB=10,E为CD上一点,连接AE,BE,AE⊥BE,AE=6,点P从点A出发,沿A→E→B的路径匀速运动到点B停止,作PQ⊥CD于点Q,设点P运动的路程为x,PQ长为y,则y与x之间的函数图象大致为( )
第10题图
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 40-|-3|=________.
12. 若代数式在实数范围内有意义,则x的取值范围为__________.
13. 如图,在平面直角坐标系中,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至CD,则a+b的值为________.
第13题图
14. 如图,某学校“桃李餐厅”把WIFI密码做成了数学题.小红在餐厅就餐时,思索了一会儿,输入密码,顺利地连接到了“桃李餐厅”的网络.那么她输入的密码是__________.
第14题图
15. 如图①,分别沿矩形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图②所示的 KLMN,若中间空白部分四边形OPQR恰好是正方形,且 KLMN的面积为40,则正方形EFGH的面积为________.
第15题图
16. 已知抛物线y=ax2+bx+c(a,b,c是常数),a+b+c=0.下列四个结论:①若抛物线经过点(-3,0),则b=2a;②若b=c,则方程cx2+bx+a=0一定有根x=2;③抛物线与x轴一定有两个交点;④点A(x1,y1),B(x2,y2)在抛物线上,若0<a<c,则当x1<x2<1时,y1>y2.其中正确的是________(填写序号).
班级:________ 姓名:________ 得分:________
题组特训 六
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. 25的算术平方根是( )
A. -5 B. 5
C. ±5 D.
2. 下列图形既不是中心对称图形也不是轴对称图形的是( )
3. 如图,数轴(单位长度为1)上有三个点A,B,C,若点A,B表示的数互为相反数,则图中点C对应的数是( )
第3题图
A. 4 B. 1 C. 0 D. -2
4. 如图是一个六角螺栓,它的俯视图是( )
5. 在一次古诗词朗读比赛中,七位评委给小明打了互不相同的7个分数,若去掉一个最高分,平均分为a;若去掉一个最低分,平均分为b;若同时去掉一个最高分和一个最低分,平均分为c,则( )
A. a>b>c B. b>a>c
C. b>c>a D. c>a>b
6. 关于x的一元二次方程(a+1)x2+bx+1=0有两个相等的实数根,则代数式12a-3b2+4的值是( )
A. 8 B. -8
C. 4 D. -4
7. 如图,把量角器摆放在△AOC上,点A与点C恰在同一个半圆上,OC与130°的刻度线重合,射线OB与70°的刻度线重合,OB交AC于点D,则∠CDO的度数为( )
第7题图
A. 90° B. 95°
C. 100° D. 120°
8. 如图,在边长为1个单位的正方形网格中建立平面直角坐标系,已知点A,B,C,D均在网格格点上.将线段AB绕点P旋转一定角度后与线段CD重合(点A与点C重合,点B与点D重合),则旋转中心P的坐标是( )
第8题图
A. (-2,1) B. (-1,2)
C. (-2,-1) D. (-1,-2)
9. 如图,将平行四边形ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F,若∠B=80°,∠ACE=2∠ECD,FC=3,FD=1,则平行四边形ABCD的周长为( )
第9题图
A. 16 B. 14
C. 12 D. 10
10. 二次函数y=ax2+bx+c的图象如图所示,则下列结论:①抛物线与x轴的另一个交点的横坐标x>-3;②a=b+2;③b2-4ac<-8a;④当a=-1时,将抛物线先向下平移1个单位,再向左平移2个单位,得到的新抛物线与y轴的交点坐标为(0,-5).其中正确的是( )
第10题图
A. ①② B. ①③
C. ①④ D. ①②③④
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 2022年6月5日,神舟十四号载人飞船在酒泉卫星发射中心发射成功,飞船入轨后将按照预定程序与离地面约400000米的天宫空间站进行对接.请将400000米用科学记数法表示为____________米.
12. 分解因式:4a2+8a+4=____________.
13. 已知不等式组在同一条数轴上表示不等式①②的解集如图所示,则5a-3b的值为 ________.
第13题图
14. 在△ABC中,若|cos A-|+|tan B-1|=0,则∠C的度数为________.
15. 如图,在直角坐标系中,O为坐标原点,函数y=与y=在第一象限的图象分别为曲线l1,l2,点P为曲线l1上的任意一点,过点P作y轴的垂线交l2于点A,作x轴的垂线交l2于点B,则△AOB的面积是________.
第15题图
16. 如图,正方形ABCD的边长为4,分别以点B,C为圆心,BC长为半径作弧,两弧在正方形ABCD内部交于点F,以点B为圆心,BD为半径作弧,交BC的延长线于点E,则图中阴影部分的面积为________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 七
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. |-2022|的结果为( )
A. - B.
C. -2022 D. 2022
2. 下列4个数字中,是中心对称图形但不是轴对称图形的是( )
3. 下列几何体的主视图和俯视图完全相同的是( )
4. 下列说法正确的是( )
A. 经过有交通信号灯的十字路口,遇到绿灯是随机事件
B. 抛一枚质地均匀的硬币刚好正面朝上是必然事件
C. 购买一张彩票中奖是不可能事件
D. “清明时节雨纷纷”是必然事件
5. 微米是一种长度单位,它用来表示微小的长度,1微米=10-6米,一根头发丝的直径约为70微米,则一根头发丝的直径用科学记数法表示为( )
A. 70×10-6 B. 7×10-5
C. 7×10-4 D. 0.7×10-7
6. 如图,若 ABCD的顶点A,C,D的坐标分别是(-2,1),(5,0),(2,-2),则点B的坐标为( )
第6题图
A. (3,-1) B. (4,-1)
C. (1,4) D. (1,3)
7. 甲、乙两名同学本学期五次引体向上的测试成绩(个数)如图所示,下列判断错误的是( )
第7题图
A. 甲成绩的众数为8个
B. 甲成绩与乙成绩的平均数相同
C. 乙成绩的中位数为7个
D. 甲的成绩比乙的成绩稳定
8. 如图,点C,D在以AB为直径的半圆上,且∠ACD=110°,点E是上任意一点,连接BE,DE,则∠BED的度数为( )
第8题图
A. 15° B. 20° C. 25° D. 30°
9. 如图,抛物线y=ax2+bx+c(a,b,c为常数且a≠0)交x轴于点A(-2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论错误的是( )
第9题图
A. c=2b+2 B. a=
C. b=ac+1 D. <0
10. 如图,等边△ABC、等边△DEF的边长分别为3和2.开始时点A与点D重合,DE在AB上,DF在AC上,△DEF沿AB向右平移,当点D到达点B时停止.在此过程中,设△ABC,△DEF重合部分的面积为y,△DEF移动的距离为x,则y与x的函数图象大致为( )
第10题图
A B
C D
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 计算:-(-)-1=________.
12. 已知一个正多边形的内角和为1440°,则它的一个外角的度数为________.
13. 若关于x的一元二次方程x2-(2m-1)x+m2-2m=0有两个不相等的实数根,则m的取值范围是________.
14. 如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为6,则k的值为________.
第14题图
15. 如图,在正方形ABCD中,AB=9,M是AD边上的一点,AM∶AD=1∶3,连接BM,将△BMA沿BM对折至△BMN,连接DN,则DN的长是________ .
第15题图
16. 如图,从一块边长为4,∠A=120°的菱形铁片上剪出一个扇形,这个扇形在以A为圆心的圆上(阴影部分),且圆弧与BC,CD分别相切于点E,F,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径是________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 八
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. 下列实数中,为有理数的是( )
A. B. 0.010010001
C. D. π
2. 下列图形既是中心对称图形又是轴对称图形的是( )
3. 下列运算正确的是( )
A. x4·x=x4
B. (x2)3=x6
C. 6x6÷x2=6x3
D. x2+x3=x5
4. 一个几何体的三视图如图所示,则这个几何体是( )
5. 一个多边形的内角和是外角和的3倍,则这个多边形是( )
A. 八边形
B. 九边形
C. 十边形
D. 十二边形
6. 利用我们数学课本上的计算器计算sin 40°,正确的按键顺序是( )
A.
B.
C.
D.
7. 如图是一组有规律的图案,第1个图案由3个正方形组成,第2个图案由7个正方形组成,…,按此规律,第n个图案中正方形的个数为( )
第7题图
A. 3n-2 B. 4n+1
C. 4n-1 D. 3n+1
8. 如图,丽丽用边长为4的正方形做了一套七巧板,小组合作将这套七巧板拼成了“人”的形状,则这个“人”的两只脚的面积S1与七巧板总面积S的比值为( )
第8题图
A. B.
C. D.
9. 如图,CD是△ABC的角平分线,AE⊥CD于点E,BC=6,AC=4,△AEC的面积是3,则△ABC的面积为( )
第9题图
A. 9 B. 11
C. 12 D. 15
10. 如图,一次函数y=kx+b(k≠0)的图象与x轴交于点A,与y轴交于点B,与双曲线y=在第一象限交于点C,过点C作CD⊥x轴于点D,若AO=DO,△AOB的面积为1,则k的值为( )
第10题图
A. 8 B. 6
C. 4 D. 2
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 实数a,b在数轴上对应点的位置如图所示,则a+b的绝对值为________.
第11题图
12. 若关于x的一元二次方程x2-ax+6=0的一个根是3,则a的值为________.
13. 古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2米,它的影长FD是4米,同一时刻测得OA是268米,则金字塔的高度BO是__________米.
第13题图
14. 在一个不透明的口袋中装有6个大小相同的小球,其中白球有2个,红球有1个,黄球有3个,从口袋中随机摸出一个小球,摸到白球的概率为________.
15. 如图,在平面直角坐标系中,△ABC与△DEF是位似图形,则它们的位似中心的坐标为________.
第15题图
16. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2-4ac>0;②4a+c>2b;③若点A(-2,y1),点B(,y2),点C(,y3)在该函数图象上,则y1<y2<y3;④若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确结论的序号为________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 九
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. -27的立方根是( )
A. 3 B. -3
C. ±3 D. 3
2. 下面图形中,是中心对称图形的是( )
3. 实数a,b在数轴上的位置如图所示,则下列结论不正确的是( )
第3题图
A. <0 B. |b|>2
C. a+b>0 D. a>b
4. 如图是一个正方体中间挖出一个圆柱体后的剩余部分,则该几何体的左视图是( )
5. 按如图所示的程序计算函数y的值,若输入的x的值为1,则输出的y的值为-1,若输入的x的值为6,则输出的y的值为( )
第5题图
A. 9 B. 12
C. 15 D. 18
6. 已知关于x的一元二次方程x2+2x=a-2有两个相等的实数根,则实数a的值为( )
A. 0 B. 1
C. 3 D. 1或3
7. 如图是对边互相平行的六边形ABCDEF,若∠ABC=120°,∠AFE=108°,则∠CDE的度数为( )
第7题图
A. 132° B. 134°
C. 144° D. 128°
8. 在对一组样本数据进行分析时,小华列出了方差的计算公式:s2=[(6-x)2+(7-x)2+(8-x)2+(8-x)2+(9-x)2],由公式提供的信息,则下列说法错误的是( )
A. 样本的容量是5
B. 样本的中位数是8
C. 样本的众数是8
D. 样本的平均数是7
9. 如图,在菱形ABCD中,AB=8,∠A=60°,点M是边AD的中点,连接MC,将菱形ABCD沿MN翻折,使点A落在线段CM上的点E处,折痕交AB于点N,则线段EC的长为( )
第9题图
A. 4-4 B. 4
C. D. 2-2
10. 已知抛物线y=ax2+bx+c,其中x与y的部分对应值如下表:
x … -1 0 2 4 5 …
y … 0 -5 -9 -5 0 …
下列结论:①抛物线开口向上;②抛物线的顶点坐标为(2,-9);③若关于x的方程ax2+bx+c=0的两根为x1,x2,则x1+x2=4;④若点(,y1)和点(,y2)在抛物线上,则y1<y2. 其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. “戴口罩、勤洗手、常通风”能够有效地预防新冠病毒,保护自身健康安全,N95型口罩对空气动力学直径为0.000075 mm±0.000020 mm的颗粒的过滤效率达到95%以上.其中数据0.000075用科学记数法可表示为________.
12. 若关于x的分式方程-5=有增根,则a的值为________.
13. 如图,在平面直角坐标系中,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点A(-2,0)的对应点D的坐标为________.
第13题图
14. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠BAC,点P,Q分别是AD,AB的中点,若CP=,则PQ的长为 ________ .
第14题图
15. 如图,△OAB的边OB在x轴上,反比例函数y=(x>0)的图象经过点A,交AB于点C,且AC=2BC,则△OAB的面积为________.
第15题图
16. 如图,在扇形ABC中,∠ABC=120°,AB=2,将扇形ABC绕点A沿顺时针方向旋转到扇形ADE的位置,点B的对应点D落在上,则图中阴影部分的面积为________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 十
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. 若x的倒数为,则x的值为( )
A. - B.
C. -7 D. 7
2. 下列字母中,是轴对称图形但不是中心对称图形的是( )
3. 随着我国社保事业的快速发展,养老保险已经完成基本覆盖,截至2021年底,全国社保卡持卡人数达到13.52亿人,将数据13.52亿用科学记数法表示为( )
A. 0.1352×109 B. 1.352×109
C. 13.52×108 D. 1.352×107
4. 图中三视图所对应的几何体是( )
5. 如图,直线AB∥CD,EM⊥PM于点M,若∠CEF=120°,则∠APM的度数为( )
第5题图
A. 45° B. 40°
C. 35° D. 30°
6. 甲、乙、丙、丁四位同学在最近5次1 min跳绳练习中,平均成绩都是115次,方差分别是s=2.4,s=2.1,s=3.5,s=4.3,若从中选一名成绩好且发挥稳定的学生参加运动会,则应选( )
A. 甲 B. 乙
C. 丙 D. 丁
7. 如图,△ABC是边长为2的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B与点D1重合,折痕GH交BD1于点D2,…,依次折叠,则BD6的长为( )
第7题图
A. B.
C. D.
8. 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
第8题图
A. (-2,-1) B. (2,1)
C. (1,-1) D. (-1,-1)
9. 如图,AB,CD是⊙O的两条直径,E是劣弧BC的中点,连接BC,DE.若∠ABC=22°,则∠CDE的度数为( )
第9题图
A. 22° B. 32°
C. 34° D. 44°
10. 如图,二次函数y=ax2+bx+c(a,b,c为常数且a≠0)图象的对称轴为直线x=1,下列结论:①b2-4ac>0;②9a+3b+c<0;③(a+c)2<b2;④a+b<m(am+b)(其中m是不等于1的实数).其中正确的个数是( )
第10题图
A. 4个 B. 3个
C. 2个 D. 1个
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 化简:(-a2b3)2=________.
12. 若与(9+3n)2互为相反数,则m-n=________.
13. 如图,按以下步骤作图:①在数轴及其上方,作长为2,宽为1矩形的对角线OP;②以点O为圆心,OP长为半径顺时针作弧,交数轴于点Q,则点Q代表的实数为________.
第13题图
14. 关于x的一元二次方程kx2+5x-2=0有实数根,则k的取值范围是________.
15. 如图,一次函数y=kx+b(k>0)的图象过点(-1,0),则不等式k(x+1)+b<0的解集是________.
第15题图
16. 中国古代数学家刘徽在《九章算术注》中,给出了证明三角形面积公式的出入相补法. 如图所示,在△ABC中,分别取AB,AC的中点D,E,连接DE,过点A作AF⊥DE,垂足为F,将△ABC分割后拼接成矩形BCHG. 若DE=6,AF=4,则矩形BCHG的面积是________.
第16题图
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. 下列4个实数中,为无理数的是( )
A. - B. C. D. 3.14
2. 下列分别是山东、重庆、江苏、甘肃电视台的标志,其中是中心对称图形但不是轴对称图形的是( )
3. 下列运算结果是m8的是( )
A. m2·m4 B. (m4)2
C. m4+m4 D. m16÷m2
4. 如图是由一个长方体和一个圆锥组成的几何体,则它的俯视图是( )
5. 若正多边形的一个外角是72°,则该正多边形的内角和为( )
A. 900° B. 720°
C. 540° D. 360°
6. 在某市组织的物理实验操作考试中,考试所用实验室共有24个测试位,分成6组,同组4个测试位各有一道相同试题,各组的试题不同,分别标记为A,B,C,D,E,F,考生从中随机抽取一道试题,则某个考生抽到试题A的概率为( )
A. B. C. D.
7. 如图,在Rt△ABC中,∠C=90°,AF=EF,若∠B=54°,则∠CFE的度数为( )
第7题图
A. 72°
B. 76°
C. 82°
D. 86°
8. 关于x的方程(m-1)2x2+(2m-1)x+1=0没有实数根,则m的取值范围是( )
A. m<且m≠-1 B. m<
C. m> D. m≤且m≠-1
9. 我国南宋数学家杨辉所著的《详解九章算法》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.根据“杨辉三角”请计算(a+b)10的展开式中第三项的系数为( )
第9题图
A. 45 B. 50 C. 55 D. 60
10. 如图,抛物线y=ax2+bx+c的对称轴为直线x=2,下列结论:①abc>0;②4a-c>0;③9a-3b+c<0; ④若点(-0.5,y1), (-2,y2)均在抛物线上,则y1>y2. 其中正确的个数为( )
第10题图
A. 1个 B. 2个
C. 3个 D. 4个
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 把x2-4x+4因式分解为__________.
12. 如图,这是一个利用平面直角坐标系画出的某学校的示意图,如果这个坐标系分别以正东、正北方向为x轴,y轴的正方向,并且综合楼和食堂的坐标分别是(4,1)和(5,4),则教学楼的坐标是__________.
第12题图
13. 运行程序如图所示,从“输入实数x”到“结果是否>8”为一次操作程序,若输入x后程序操作仅进行了一次就停止,则x的取值范围是________.
第13题图
14. 如图,△ABC内接于⊙O,且AB是⊙O的直径,点D是△ABC的内心,连接CD并延长交⊙O于点E,连接BD,若∠BAC=50°,则∠BDE的度数为______.
第14题图
15. 根据物理学知识,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其函数图象如图所示.当S=0.25 m2时,该物体承受的压强p的值为______Pa.
第15题图
16. 如图①,在四边形ABCD中,BC∥AD,∠D=90°,∠A=45°,动点P,Q同时从点A出发,点P以cm/s的速度沿AB向点B运动(运动到B点即停止),点Q以2 cm/s的速度沿折线AD→DC向终点C运动,设点Q的运动时间为x(s),△APQ的面积为y(cm2),若y与x之间的函数关系的图象如图②所示,当x=(s)时,则y=______cm2.
图①
图②
第16题图
班级:________ 姓名:________ 得分:________
题组特训 二
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. -5的绝对值是( )
A. 5 B. -5 C. D. -
2. 下列四幅图案是四所大学校徽的主体标识,既是轴对称图形,又是中心对称图形的是( )
3. 下列运算正确的是( )
A. 6a2-5a2=1
B. a2·a4=a8
C. (a+b)(a-b)=a2-b2
D. (-3a4)2=-9a8
4. 如图①是由5个完全相同的小正方体组成的立体图形,将上层的小正方体平移后得到图 ②,则关于平移前后几何体的三视图发生改变的是( )
第4题图
A. 主视图
B. 俯视图
C. 左视图
D. 主视图、俯视图和左视图都发生改变
5. 直角三角板如图摆放在两条平行线上,若∠1=21°,则∠2的度数为( )
第5题图
A. 159° B. 146°
C. 114° D. 156°
6. 若用我们数学课本上采用的科学计算器进行计算,其按键顺序及结果如下:
下列判断正确的是( )
A. a>b B. a=b
C. a<b D. 无法确定
7. 函数y=kx+b的图象如图所示,则关于x的一元二次方程x2+kx+b-1=0的根的情况是( )
A. 没有实数根
B. 有两个相等的实数根
C. 有两个不相等的实数根
D. 无法确定
第7题图
8. 如图,在平行四边形ABCD中,E为BC的中点,BD,AE交于点O,若随机向平行四边形ABCD内投一粒米,则米粒落在图中阴影部分的概率为( )
A. B. C. D.
第8题图
9. 已知二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则下列结论中错误的是( )
第9题图
A. bc<0
B. 2a-b>0
C. b2>(a+c)2
D. 点(-3,y1),(1,y2)都在二次函数的图象上,则有y1
第10题图
A. ()7 B. ()8
C. ()7 D. ()8
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 若代数式在实数范围内有意义,则x的取值范围为________.
12. 《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步. 问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?设有x辆车,人数为y,根据题意可列方程组为______________.
13. 如图,A,B,C,D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=20°,则这个正多边形的边数为________.
第13题图
14. 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图①就是一个幻方.图②是一个未完成的幻方,则x与y的和是__________.
图①
图②
第14题图
15. 如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D是上任意一点,则cos ∠ADC=________.
第15题图
16. 如图①,一张矩形纸片ABCD,点E,F分别在AB,CD上,点G,H分别在AF,EC上,现将该纸片沿AF,GH,EC剪开,拼成如图②所示的矩形,已知DF∶AD=5∶12,GH=6,则AD的长是________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 三
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. -的相反数是( )
A. B. -
C. D. -
2. 下列垃圾分类图标中,其文字上方的图案是轴对称图形,但不是中心对称图形的是( )
3. 如图,在数轴上,点A,B分别表示的数为-4,2,点C是AB的中点,则点C表示的数为( )
第3题图
A. -1 B. 1
C. D. -
4. 如图是由正六棱柱和球体组合而成的几何体,其左视图是( )
5. 一组数据:2,5,5,5,8,若去掉一个数据5,则下列统计量中发生变化的是( )
A. 众数 B. 中位数
C. 平均数 D. 方差
6. 利用科学计算器进行计算,小明的按键顺序为,则计算器显示的结果最接近的一个数是( )
A. 3 B. 4 C. 5 D. 6
7. 如图,某链条每节长为2.8 cm,每两节链条相连接部分重叠的圆的直径为1 cm,按这种连接方式,50节链条总长度为( )
第7题图
A. 81 cm B. 80 cm
C. 91 cm D. 90 cm
8. 如图,在△ABC中,AC=BC,∠A=65°,分别以点B,C为圆心,大于BC的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,连接BD,则∠BDA的度数为( )
第8题图
A. 70° B. 80° C. 90° D. 100°
9. 已知关于x的一元二次方程(m-1)x2-x+1=0有两个不相等的实数根,则m可能的取值为( )
A. 3 B. 4
C. 5 D. 6
10. 如图,正比例函数y1=ax,一次函数y2=mx+n和反比例函数y3=的图象在同一平面直角坐标系中,若y3<y2<y1,则x的取值范围为( )
第10题图
A. x<-3 B. 0<x<1
C. x<-3 或0<x<1 D. -3<x<1
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 据山东省能源局消息,2022年山东省能源行业的发展目标是电力总装机达到180000000千瓦左右.将数据180000000用科学记数法表示为________.
12. 已知最简二次根式与是同类二次根式,那么a的值为________.
13. 两千多年前,古希腊数学家欧多克索斯发现了黄金分割,如图,点P是线段AB上一点(AP>BP),若满足=,则称点P是AB的黄金分割点.黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好. 若舞台长25米,主持人从舞台一侧进入,设他至少走x米时恰好站在舞台的黄金分割点上,则x满足的方程是____________ .
第13题图
14. 如图,在△ABC中,AB=AC=5,BC=6,点D在CA的延长线上,DE⊥BC于点E,若AD=2,则DE的长为________.
第14题图
15. 如图,将△ABC绕点P旋转180°得到△A′B′C′,则点P的坐标为________.
第15题图
16. 二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a>b;③(a+c)2<b2;④a-2b+4c>0,其中正确的是________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 四
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. 9的平方根是( )
A. 3 B. -3 C. ±3 D.
2. 下列由黑白棋子组成的图案中,是轴对称图形的是( )
3. 如图是沿圆柱体顶部圆的直径切去一部分之后所得到的几何体,则该几何体的主视图为( )
4. 2022年3月22日,中央一号文件《中共中央国务院关于做好2022年全面推进乡村振兴重点工作的意见》正式发布.文件中提出,要稳定全年粮食播种面积和产量,确保粮食产量保持在1.3万亿斤以上.将数据1.3万亿用科学记数法表示为 ( )
A. 0.13×1013 B. 1.3×1012
C. 1.3×108 D. 1.3×104
5. 将一枚飞镖任意投掷到如图所示的正六边形镖盘上,飞镖落在阴影区域的概率为 ( )
第5题图
A. B. C. D.
6. 如图,在 ABCD中,过点C作CE⊥BA交BA的延长线于点E,若∠EAD=52°,则∠ECB的度数为( )
第6题图
A. 52° B. 28° C. 38° D. 48°
7. 现有甲、乙、丙三种不同品种糖果的单价与千克数如下表所示:
甲种糖果 乙种糖果 丙种糖果
单价(元/千克) 14 10 8
千克数 2 3 5
将这2千克甲种糖果、3千克乙种糖果和5千克丙种糖果混合成10千克什锦糖果,若商家用加权平均数来确定什锦糖果的单价,则这10千克什锦糖果的单价为( )
A. 9.2 B. 8.9
C. 10 D. 9.8
8. 如图,∠MON=45°,在OM上截取OA1=1.过点A1作A1B1⊥OM,交ON于点B1,以点B1为圆心,B1O为半径画弧,交OM于点A2;过点A2作A2B2⊥OM,交ON于点B2,以点B2为圆心,B2O为半径画弧,交OM于点A3;…;按此规律,所得线段A22B22的长等于( )
第8题图
A. 220 B. 221
C. 222 D. 224
9. 如图,BE是△ABC的中线,点F在BE上,连接AF并延长交BC于点D.若BF=3FE,DC=2,则BD的长为( )
第9题图
A. 6 B. 5
C. 4 D. 3
10. 抛物线y=-x2+mx+n与x轴、y轴分别交于点A(-1,0),B(0,3).下列结论错误的是( )
A. 抛物线的对称轴为直线x=1
B. 抛物线与x轴的另一个交点为(3,0)
C. 方程x2-mx-n=p(p>4)无解
D. 若点(-2,y1)和(5,y2)在抛物线上,则y1>y2
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 把2x2-2因式分解为____________ .
12. 若(a+5)2+|2b-4|=0,则ab=______.
13. 关于x的一元二次方程(a+2)x2-3x+1=0有两个相等的实数根,则a的值为________.
14. 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,若点A的坐标为(0,1),点B坐标为(2,1),则这条圆弧所在圆的圆心坐标为________.
第14题图
15. 如图,在平面直角坐标系xOy中,一次函数y=-x+b的图象分别与x轴、y轴交于点C(4,0),B,与反比例函数y=(x<0)的图象交于点A,连接OA,BC=4AB.则k的值为________.
第15题图
16. 由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为2的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分). 则图中AB的长应是 __________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 五
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. -3的倒数是( )
A. - B. C. -3 D. 3
2. 下列交通标识中,既是轴对称图形,又是中心对称图形的是( )
3. 下列计算结果正确的是( )
A. 5a-3a=2
B. 6a÷2a=3a
C. a6÷a3=a2
D. (2a2b3)3=8a6b9
4. 用四个相同的小正方体搭成几何体,要求每个几何体的主视图、左视图、俯视图中至少有两种视图的形状是相同的,下列四种摆放方式中不符合要求的是( )
5. 将含30°角的三角板ABC和含45°角的三角板DEF按如图所示的位置摆放,AC交DE于点M,若BC∥EF,则∠DMC的度数为( )
第5题图
A. 85° B. 80° C. 75° D. 70°
6. 某学校准备挑选一名学生参加市级演讲比赛,在三轮学校预赛中得到甲、乙、丙、丁四名同学三轮预赛成绩的平均数x和方差s2如下表:
甲 乙 丙 丁
x 95 97 96 97
s2 0.6 1.2 1.2 0.6
根据表中数据,要从甲、乙、丙、丁四名同学中选择一名成绩好又发挥稳定的同学参赛,应该选择( )
A. 甲 B. 乙 C. 丙 D. 丁
7. 下面各图形是由大小相同的三角形摆放而成的,图①中有1个三角形,图②中有5个三角形,图③中有11个三角形,图④中有19个三角形,…,依此规律,则图 中三角形个数是( )
第7题图
A. 155 B. 156 C. 157 D. 144
8. 如图,一次函数y=kx+6(k≠0)的图象经过点A(3,0),与正比例函数y=mx的图象交于点B(a,4),则不等式kx+6>mx的解集为( )
第8题图
A. x<1 B. 1<x<3
C. x>3 D. x<1 或x>3
9. 如图,AC是⊙O的直径,弦BD⊥AC于点G,连接BC,CD,若OG=BD,则∠BCD的大小为( )
第9题图
A. 115° B. 125°
C. 135° D. 150°
10. 如图,在矩形ABCD中,AB=10,E为CD上一点,连接AE,BE,AE⊥BE,AE=6,点P从点A出发,沿A→E→B的路径匀速运动到点B停止,作PQ⊥CD于点Q,设点P运动的路程为x,PQ长为y,则y与x之间的函数图象大致为( )
第10题图
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 40-|-3|=________.
12. 若代数式在实数范围内有意义,则x的取值范围为__________.
13. 如图,在平面直角坐标系中,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至CD,则a+b的值为________.
第13题图
14. 如图,某学校“桃李餐厅”把WIFI密码做成了数学题.小红在餐厅就餐时,思索了一会儿,输入密码,顺利地连接到了“桃李餐厅”的网络.那么她输入的密码是__________.
第14题图
15. 如图①,分别沿矩形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图②所示的 KLMN,若中间空白部分四边形OPQR恰好是正方形,且 KLMN的面积为40,则正方形EFGH的面积为________.
第15题图
16. 已知抛物线y=ax2+bx+c(a,b,c是常数),a+b+c=0.下列四个结论:①若抛物线经过点(-3,0),则b=2a;②若b=c,则方程cx2+bx+a=0一定有根x=2;③抛物线与x轴一定有两个交点;④点A(x1,y1),B(x2,y2)在抛物线上,若0<a<c,则当x1<x2<1时,y1>y2.其中正确的是________(填写序号).
班级:________ 姓名:________ 得分:________
题组特训 六
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. 25的算术平方根是( )
A. -5 B. 5
C. ±5 D.
2. 下列图形既不是中心对称图形也不是轴对称图形的是( )
3. 如图,数轴(单位长度为1)上有三个点A,B,C,若点A,B表示的数互为相反数,则图中点C对应的数是( )
第3题图
A. 4 B. 1 C. 0 D. -2
4. 如图是一个六角螺栓,它的俯视图是( )
5. 在一次古诗词朗读比赛中,七位评委给小明打了互不相同的7个分数,若去掉一个最高分,平均分为a;若去掉一个最低分,平均分为b;若同时去掉一个最高分和一个最低分,平均分为c,则( )
A. a>b>c B. b>a>c
C. b>c>a D. c>a>b
6. 关于x的一元二次方程(a+1)x2+bx+1=0有两个相等的实数根,则代数式12a-3b2+4的值是( )
A. 8 B. -8
C. 4 D. -4
7. 如图,把量角器摆放在△AOC上,点A与点C恰在同一个半圆上,OC与130°的刻度线重合,射线OB与70°的刻度线重合,OB交AC于点D,则∠CDO的度数为( )
第7题图
A. 90° B. 95°
C. 100° D. 120°
8. 如图,在边长为1个单位的正方形网格中建立平面直角坐标系,已知点A,B,C,D均在网格格点上.将线段AB绕点P旋转一定角度后与线段CD重合(点A与点C重合,点B与点D重合),则旋转中心P的坐标是( )
第8题图
A. (-2,1) B. (-1,2)
C. (-2,-1) D. (-1,-2)
9. 如图,将平行四边形ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F,若∠B=80°,∠ACE=2∠ECD,FC=3,FD=1,则平行四边形ABCD的周长为( )
第9题图
A. 16 B. 14
C. 12 D. 10
10. 二次函数y=ax2+bx+c的图象如图所示,则下列结论:①抛物线与x轴的另一个交点的横坐标x>-3;②a=b+2;③b2-4ac<-8a;④当a=-1时,将抛物线先向下平移1个单位,再向左平移2个单位,得到的新抛物线与y轴的交点坐标为(0,-5).其中正确的是( )
第10题图
A. ①② B. ①③
C. ①④ D. ①②③④
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 2022年6月5日,神舟十四号载人飞船在酒泉卫星发射中心发射成功,飞船入轨后将按照预定程序与离地面约400000米的天宫空间站进行对接.请将400000米用科学记数法表示为____________米.
12. 分解因式:4a2+8a+4=____________.
13. 已知不等式组在同一条数轴上表示不等式①②的解集如图所示,则5a-3b的值为 ________.
第13题图
14. 在△ABC中,若|cos A-|+|tan B-1|=0,则∠C的度数为________.
15. 如图,在直角坐标系中,O为坐标原点,函数y=与y=在第一象限的图象分别为曲线l1,l2,点P为曲线l1上的任意一点,过点P作y轴的垂线交l2于点A,作x轴的垂线交l2于点B,则△AOB的面积是________.
第15题图
16. 如图,正方形ABCD的边长为4,分别以点B,C为圆心,BC长为半径作弧,两弧在正方形ABCD内部交于点F,以点B为圆心,BD为半径作弧,交BC的延长线于点E,则图中阴影部分的面积为________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 七
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. |-2022|的结果为( )
A. - B.
C. -2022 D. 2022
2. 下列4个数字中,是中心对称图形但不是轴对称图形的是( )
3. 下列几何体的主视图和俯视图完全相同的是( )
4. 下列说法正确的是( )
A. 经过有交通信号灯的十字路口,遇到绿灯是随机事件
B. 抛一枚质地均匀的硬币刚好正面朝上是必然事件
C. 购买一张彩票中奖是不可能事件
D. “清明时节雨纷纷”是必然事件
5. 微米是一种长度单位,它用来表示微小的长度,1微米=10-6米,一根头发丝的直径约为70微米,则一根头发丝的直径用科学记数法表示为( )
A. 70×10-6 B. 7×10-5
C. 7×10-4 D. 0.7×10-7
6. 如图,若 ABCD的顶点A,C,D的坐标分别是(-2,1),(5,0),(2,-2),则点B的坐标为( )
第6题图
A. (3,-1) B. (4,-1)
C. (1,4) D. (1,3)
7. 甲、乙两名同学本学期五次引体向上的测试成绩(个数)如图所示,下列判断错误的是( )
第7题图
A. 甲成绩的众数为8个
B. 甲成绩与乙成绩的平均数相同
C. 乙成绩的中位数为7个
D. 甲的成绩比乙的成绩稳定
8. 如图,点C,D在以AB为直径的半圆上,且∠ACD=110°,点E是上任意一点,连接BE,DE,则∠BED的度数为( )
第8题图
A. 15° B. 20° C. 25° D. 30°
9. 如图,抛物线y=ax2+bx+c(a,b,c为常数且a≠0)交x轴于点A(-2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论错误的是( )
第9题图
A. c=2b+2 B. a=
C. b=ac+1 D. <0
10. 如图,等边△ABC、等边△DEF的边长分别为3和2.开始时点A与点D重合,DE在AB上,DF在AC上,△DEF沿AB向右平移,当点D到达点B时停止.在此过程中,设△ABC,△DEF重合部分的面积为y,△DEF移动的距离为x,则y与x的函数图象大致为( )
第10题图
A B
C D
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 计算:-(-)-1=________.
12. 已知一个正多边形的内角和为1440°,则它的一个外角的度数为________.
13. 若关于x的一元二次方程x2-(2m-1)x+m2-2m=0有两个不相等的实数根,则m的取值范围是________.
14. 如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为6,则k的值为________.
第14题图
15. 如图,在正方形ABCD中,AB=9,M是AD边上的一点,AM∶AD=1∶3,连接BM,将△BMA沿BM对折至△BMN,连接DN,则DN的长是________ .
第15题图
16. 如图,从一块边长为4,∠A=120°的菱形铁片上剪出一个扇形,这个扇形在以A为圆心的圆上(阴影部分),且圆弧与BC,CD分别相切于点E,F,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径是________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 八
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. 下列实数中,为有理数的是( )
A. B. 0.010010001
C. D. π
2. 下列图形既是中心对称图形又是轴对称图形的是( )
3. 下列运算正确的是( )
A. x4·x=x4
B. (x2)3=x6
C. 6x6÷x2=6x3
D. x2+x3=x5
4. 一个几何体的三视图如图所示,则这个几何体是( )
5. 一个多边形的内角和是外角和的3倍,则这个多边形是( )
A. 八边形
B. 九边形
C. 十边形
D. 十二边形
6. 利用我们数学课本上的计算器计算sin 40°,正确的按键顺序是( )
A.
B.
C.
D.
7. 如图是一组有规律的图案,第1个图案由3个正方形组成,第2个图案由7个正方形组成,…,按此规律,第n个图案中正方形的个数为( )
第7题图
A. 3n-2 B. 4n+1
C. 4n-1 D. 3n+1
8. 如图,丽丽用边长为4的正方形做了一套七巧板,小组合作将这套七巧板拼成了“人”的形状,则这个“人”的两只脚的面积S1与七巧板总面积S的比值为( )
第8题图
A. B.
C. D.
9. 如图,CD是△ABC的角平分线,AE⊥CD于点E,BC=6,AC=4,△AEC的面积是3,则△ABC的面积为( )
第9题图
A. 9 B. 11
C. 12 D. 15
10. 如图,一次函数y=kx+b(k≠0)的图象与x轴交于点A,与y轴交于点B,与双曲线y=在第一象限交于点C,过点C作CD⊥x轴于点D,若AO=DO,△AOB的面积为1,则k的值为( )
第10题图
A. 8 B. 6
C. 4 D. 2
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 实数a,b在数轴上对应点的位置如图所示,则a+b的绝对值为________.
第11题图
12. 若关于x的一元二次方程x2-ax+6=0的一个根是3,则a的值为________.
13. 古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2米,它的影长FD是4米,同一时刻测得OA是268米,则金字塔的高度BO是__________米.
第13题图
14. 在一个不透明的口袋中装有6个大小相同的小球,其中白球有2个,红球有1个,黄球有3个,从口袋中随机摸出一个小球,摸到白球的概率为________.
15. 如图,在平面直角坐标系中,△ABC与△DEF是位似图形,则它们的位似中心的坐标为________.
第15题图
16. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2-4ac>0;②4a+c>2b;③若点A(-2,y1),点B(,y2),点C(,y3)在该函数图象上,则y1<y2<y3;④若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确结论的序号为________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 九
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. -27的立方根是( )
A. 3 B. -3
C. ±3 D. 3
2. 下面图形中,是中心对称图形的是( )
3. 实数a,b在数轴上的位置如图所示,则下列结论不正确的是( )
第3题图
A. <0 B. |b|>2
C. a+b>0 D. a>b
4. 如图是一个正方体中间挖出一个圆柱体后的剩余部分,则该几何体的左视图是( )
5. 按如图所示的程序计算函数y的值,若输入的x的值为1,则输出的y的值为-1,若输入的x的值为6,则输出的y的值为( )
第5题图
A. 9 B. 12
C. 15 D. 18
6. 已知关于x的一元二次方程x2+2x=a-2有两个相等的实数根,则实数a的值为( )
A. 0 B. 1
C. 3 D. 1或3
7. 如图是对边互相平行的六边形ABCDEF,若∠ABC=120°,∠AFE=108°,则∠CDE的度数为( )
第7题图
A. 132° B. 134°
C. 144° D. 128°
8. 在对一组样本数据进行分析时,小华列出了方差的计算公式:s2=[(6-x)2+(7-x)2+(8-x)2+(8-x)2+(9-x)2],由公式提供的信息,则下列说法错误的是( )
A. 样本的容量是5
B. 样本的中位数是8
C. 样本的众数是8
D. 样本的平均数是7
9. 如图,在菱形ABCD中,AB=8,∠A=60°,点M是边AD的中点,连接MC,将菱形ABCD沿MN翻折,使点A落在线段CM上的点E处,折痕交AB于点N,则线段EC的长为( )
第9题图
A. 4-4 B. 4
C. D. 2-2
10. 已知抛物线y=ax2+bx+c,其中x与y的部分对应值如下表:
x … -1 0 2 4 5 …
y … 0 -5 -9 -5 0 …
下列结论:①抛物线开口向上;②抛物线的顶点坐标为(2,-9);③若关于x的方程ax2+bx+c=0的两根为x1,x2,则x1+x2=4;④若点(,y1)和点(,y2)在抛物线上,则y1<y2. 其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. “戴口罩、勤洗手、常通风”能够有效地预防新冠病毒,保护自身健康安全,N95型口罩对空气动力学直径为0.000075 mm±0.000020 mm的颗粒的过滤效率达到95%以上.其中数据0.000075用科学记数法可表示为________.
12. 若关于x的分式方程-5=有增根,则a的值为________.
13. 如图,在平面直角坐标系中,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点A(-2,0)的对应点D的坐标为________.
第13题图
14. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠BAC,点P,Q分别是AD,AB的中点,若CP=,则PQ的长为 ________ .
第14题图
15. 如图,△OAB的边OB在x轴上,反比例函数y=(x>0)的图象经过点A,交AB于点C,且AC=2BC,则△OAB的面积为________.
第15题图
16. 如图,在扇形ABC中,∠ABC=120°,AB=2,将扇形ABC绕点A沿顺时针方向旋转到扇形ADE的位置,点B的对应点D落在上,则图中阴影部分的面积为________.
第16题图
班级:________ 姓名:________ 得分:________
题组特训 十
(分值: 48分)
一、选择题(本大题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. 若x的倒数为,则x的值为( )
A. - B.
C. -7 D. 7
2. 下列字母中,是轴对称图形但不是中心对称图形的是( )
3. 随着我国社保事业的快速发展,养老保险已经完成基本覆盖,截至2021年底,全国社保卡持卡人数达到13.52亿人,将数据13.52亿用科学记数法表示为( )
A. 0.1352×109 B. 1.352×109
C. 13.52×108 D. 1.352×107
4. 图中三视图所对应的几何体是( )
5. 如图,直线AB∥CD,EM⊥PM于点M,若∠CEF=120°,则∠APM的度数为( )
第5题图
A. 45° B. 40°
C. 35° D. 30°
6. 甲、乙、丙、丁四位同学在最近5次1 min跳绳练习中,平均成绩都是115次,方差分别是s=2.4,s=2.1,s=3.5,s=4.3,若从中选一名成绩好且发挥稳定的学生参加运动会,则应选( )
A. 甲 B. 乙
C. 丙 D. 丁
7. 如图,△ABC是边长为2的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B与点D1重合,折痕GH交BD1于点D2,…,依次折叠,则BD6的长为( )
第7题图
A. B.
C. D.
8. 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
第8题图
A. (-2,-1) B. (2,1)
C. (1,-1) D. (-1,-1)
9. 如图,AB,CD是⊙O的两条直径,E是劣弧BC的中点,连接BC,DE.若∠ABC=22°,则∠CDE的度数为( )
第9题图
A. 22° B. 32°
C. 34° D. 44°
10. 如图,二次函数y=ax2+bx+c(a,b,c为常数且a≠0)图象的对称轴为直线x=1,下列结论:①b2-4ac>0;②9a+3b+c<0;③(a+c)2<b2;④a+b<m(am+b)(其中m是不等于1的实数).其中正确的个数是( )
第10题图
A. 4个 B. 3个
C. 2个 D. 1个
二、填空题(本大题共6个小题,每小题3分,满分18分)
11. 化简:(-a2b3)2=________.
12. 若与(9+3n)2互为相反数,则m-n=________.
13. 如图,按以下步骤作图:①在数轴及其上方,作长为2,宽为1矩形的对角线OP;②以点O为圆心,OP长为半径顺时针作弧,交数轴于点Q,则点Q代表的实数为________.
第13题图
14. 关于x的一元二次方程kx2+5x-2=0有实数根,则k的取值范围是________.
15. 如图,一次函数y=kx+b(k>0)的图象过点(-1,0),则不等式k(x+1)+b<0的解集是________.
第15题图
16. 中国古代数学家刘徽在《九章算术注》中,给出了证明三角形面积公式的出入相补法. 如图所示,在△ABC中,分别取AB,AC的中点D,E,连接DE,过点A作AF⊥DE,垂足为F,将△ABC分割后拼接成矩形BCHG. 若DE=6,AF=4,则矩形BCHG的面积是________.
第16题图
同课章节目录
