2023-2024学年沪科版八年级上册数学期末复习试卷(无答案)
文档属性
| 名称 | 2023-2024学年沪科版八年级上册数学期末复习试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 247.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 11:39:09 | ||
图片预览


文档简介
2023-2024学年沪科新版八年级上册数学期末复习试卷
一.选择题(共10小题,满分40分,每小题4分)
1已知,,的面积是,那么中边上的高是( )
A. B. C. D.
2如图,平分,,点是上的动点若,则的长可以是( )
A. B. C. D.
3等腰三角形一边的长为,周长是,则底边的长是( )
A. B. C. 或 D. 或
4、如图,AB//DE,AC//DF,AC=DF,下列条件中,不能判定△ABC≌△DEF的是( )
A.AB=DE B.∠B=∠E C.EF=BC D.EF//BC
5.下列说法中,属于真命题的是( )
A.垂线最短
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角一定是对顶角
D.两直线相交,邻补角相等
6.已知直线y=mx+3(m≠0)经过点(1,0),则关于x的不等式mx+3>0的解集是( )
A.x<1 B.x>1 C.x<3 D.x>3
7.如图,在中,厘米,厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上,由C点向A点运动,为了使,点Q的运动速度应为( )
A.1厘米/秒 B.2厘米/秒 C.3厘米/秒 D.4厘米/秒
8.如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为( )
A.5 B.6 C.8 D.10
9如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )
A.2 B.3 C.4 D.无法确定
10 如图,已知,点、、…在射线ON上,点、、…在射线OM上,、、…均为等边三角形,若,则的边长为( )
A. 16 B. 64 C. 128 D. 256
二.填空题(共5小题,满分20分,每小题4分)
1.已有两根长度分别为4cm、7cm的木棒,请你再选取一根木棒,使得三根木棒首尾相接可以拼成一个三角形,你选取的木棒长度是 cm.
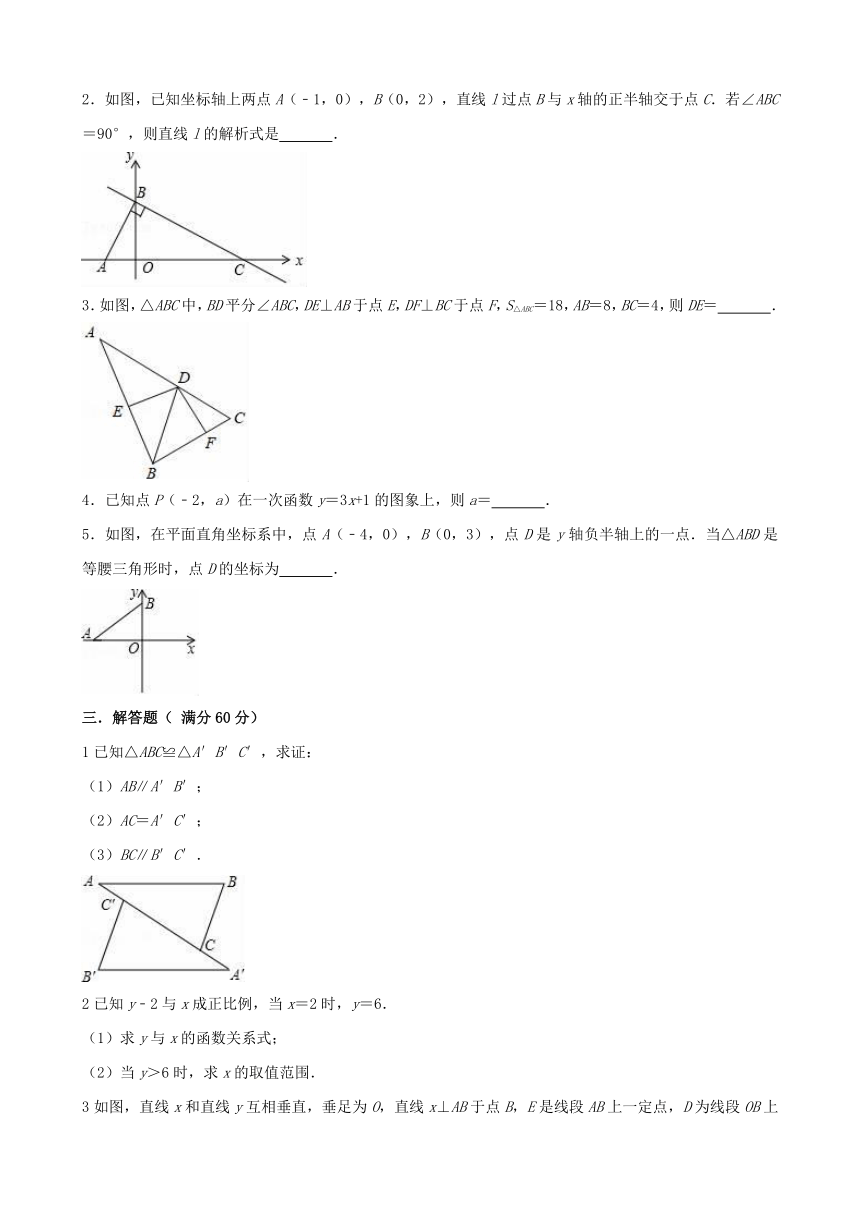
2.如图,已知坐标轴上两点A(﹣1,0),B(0,2),直线l过点B与x轴的正半轴交于点C.若∠ABC=90°,则直线l的解析式是 .
3.如图,△ABC中,BD平分∠ABC,DE⊥AB于点E,DF⊥BC于点F,S△ABC=18,AB=8,BC=4,则DE= .
4.已知点P(﹣2,a)在一次函数y=3x+1的图象上,则a= .
5.如图,在平面直角坐标系中,点A(﹣4,0),B(0,3),点D是y轴负半轴上的一点.当△ABD是等腰三角形时,点D的坐标为 .
三.解答题( 满分60分)
1已知△ABC≌△A′B′C′,求证:
(1)AB∥A′B′;
(2)AC=A′C′;
(3)BC∥B′C′.
2已知y﹣2与x成正比例,当x=2时,y=6.
(1)求y与x的函数关系式;
(2)当y>6时,求x的取值范围.
3如图,直线x和直线y互相垂直,垂足为O,直线x⊥AB于点B,E是线段AB上一定点,D为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC.
(1)当∠BED=50°,则∠OCD= °;
(2)当∠CDO=∠A时,请判断CD与AC的位置关系,并说明理由;
(3)若∠BED、∠DCO的角平分线的交点为P,当点D在线段OB上运动时,问∠P的大小是否会发生变化?若不变,求出∠P的大小,并说明理由;若变化,求其变化范围.
4如图,在平面直角坐标系中,△ABC的三个顶点的位置如图所示.
(1)若△ABC内有一点P(a,b)随着△ABC平移后到了点P′(a+4,b﹣1),直接写出A点平移后对应点A′的坐标.
(2)直接作出△ABC关于y轴对称的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点)
(3)求四边形ABC′C的面积.
5尺规作图(不写作法,但保留作图痕迹)
如图:在△ABC中,∠A=30°,∠B=40°
(1)作∠B的平分线交AC于点D;
(2)作BC边上的高AE;
(3)在完成作图后,图中∠CAE= °.
6A,B两个红十字会分别有100吨和120吨生活物资,准备直接运送给甲、乙
两个灾区,甲地需160吨,乙地需60吨,A,B两地到甲、乙两地的路程以及每吨每千米的运费如图所示.
(1)设A红十字会运往甲地物资x吨,完成如表,
运费 红十字会 灾区 运量(吨) 运费 (元)
红十字会A 红十字会B 红十字会A 红十字会B
甲地 x 160﹣x 1.3×30x 20×1.5(160﹣x)
乙地
(2)求总运费y关于x的函数表达式,并写出自变量x的取值范围.
(3)当A、B两红十字会各运往甲、乙两地多少吨物资时,总运费最省?最省运费是多少元?
7如图,△ABC和△DEF是两个等腰直角三角形,∠BAC=∠DFE=90°,AB=AC,FD=FE,△DEF的顶点E在边BC上移动,在移动过程中,线段DE与线段AB相交于点P,线段EF与线段CA相交于点Q.
(1)如图1,当E为BC中点,且BP=CQ时,求证:△BPE≌△CQE;
(2)如图2,当ED经过点A,且BE=CQ时,求∠EAQ的度数;
(3)如图3,当E为BC中点,连接AE、PQ,若AP=3,AQ=4,PQ=5,求AC的长.
一.选择题(共10小题,满分40分,每小题4分)
1已知,,的面积是,那么中边上的高是( )
A. B. C. D.
2如图,平分,,点是上的动点若,则的长可以是( )
A. B. C. D.
3等腰三角形一边的长为,周长是,则底边的长是( )
A. B. C. 或 D. 或
4、如图,AB//DE,AC//DF,AC=DF,下列条件中,不能判定△ABC≌△DEF的是( )
A.AB=DE B.∠B=∠E C.EF=BC D.EF//BC
5.下列说法中,属于真命题的是( )
A.垂线最短
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角一定是对顶角
D.两直线相交,邻补角相等
6.已知直线y=mx+3(m≠0)经过点(1,0),则关于x的不等式mx+3>0的解集是( )
A.x<1 B.x>1 C.x<3 D.x>3
7.如图,在中,厘米,厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上,由C点向A点运动,为了使,点Q的运动速度应为( )
A.1厘米/秒 B.2厘米/秒 C.3厘米/秒 D.4厘米/秒
8.如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为( )
A.5 B.6 C.8 D.10
9如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )
A.2 B.3 C.4 D.无法确定
10 如图,已知,点、、…在射线ON上,点、、…在射线OM上,、、…均为等边三角形,若,则的边长为( )
A. 16 B. 64 C. 128 D. 256
二.填空题(共5小题,满分20分,每小题4分)
1.已有两根长度分别为4cm、7cm的木棒,请你再选取一根木棒,使得三根木棒首尾相接可以拼成一个三角形,你选取的木棒长度是 cm.
2.如图,已知坐标轴上两点A(﹣1,0),B(0,2),直线l过点B与x轴的正半轴交于点C.若∠ABC=90°,则直线l的解析式是 .
3.如图,△ABC中,BD平分∠ABC,DE⊥AB于点E,DF⊥BC于点F,S△ABC=18,AB=8,BC=4,则DE= .
4.已知点P(﹣2,a)在一次函数y=3x+1的图象上,则a= .
5.如图,在平面直角坐标系中,点A(﹣4,0),B(0,3),点D是y轴负半轴上的一点.当△ABD是等腰三角形时,点D的坐标为 .
三.解答题( 满分60分)
1已知△ABC≌△A′B′C′,求证:
(1)AB∥A′B′;
(2)AC=A′C′;
(3)BC∥B′C′.
2已知y﹣2与x成正比例,当x=2时,y=6.
(1)求y与x的函数关系式;
(2)当y>6时,求x的取值范围.
3如图,直线x和直线y互相垂直,垂足为O,直线x⊥AB于点B,E是线段AB上一定点,D为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC.
(1)当∠BED=50°,则∠OCD= °;
(2)当∠CDO=∠A时,请判断CD与AC的位置关系,并说明理由;
(3)若∠BED、∠DCO的角平分线的交点为P,当点D在线段OB上运动时,问∠P的大小是否会发生变化?若不变,求出∠P的大小,并说明理由;若变化,求其变化范围.
4如图,在平面直角坐标系中,△ABC的三个顶点的位置如图所示.
(1)若△ABC内有一点P(a,b)随着△ABC平移后到了点P′(a+4,b﹣1),直接写出A点平移后对应点A′的坐标.
(2)直接作出△ABC关于y轴对称的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点)
(3)求四边形ABC′C的面积.
5尺规作图(不写作法,但保留作图痕迹)
如图:在△ABC中,∠A=30°,∠B=40°
(1)作∠B的平分线交AC于点D;
(2)作BC边上的高AE;
(3)在完成作图后,图中∠CAE= °.
6A,B两个红十字会分别有100吨和120吨生活物资,准备直接运送给甲、乙
两个灾区,甲地需160吨,乙地需60吨,A,B两地到甲、乙两地的路程以及每吨每千米的运费如图所示.
(1)设A红十字会运往甲地物资x吨,完成如表,
运费 红十字会 灾区 运量(吨) 运费 (元)
红十字会A 红十字会B 红十字会A 红十字会B
甲地 x 160﹣x 1.3×30x 20×1.5(160﹣x)
乙地
(2)求总运费y关于x的函数表达式,并写出自变量x的取值范围.
(3)当A、B两红十字会各运往甲、乙两地多少吨物资时,总运费最省?最省运费是多少元?
7如图,△ABC和△DEF是两个等腰直角三角形,∠BAC=∠DFE=90°,AB=AC,FD=FE,△DEF的顶点E在边BC上移动,在移动过程中,线段DE与线段AB相交于点P,线段EF与线段CA相交于点Q.
(1)如图1,当E为BC中点,且BP=CQ时,求证:△BPE≌△CQE;
(2)如图2,当ED经过点A,且BE=CQ时,求∠EAQ的度数;
(3)如图3,当E为BC中点,连接AE、PQ,若AP=3,AQ=4,PQ=5,求AC的长.
同课章节目录
