一次函数的图像2
图片预览



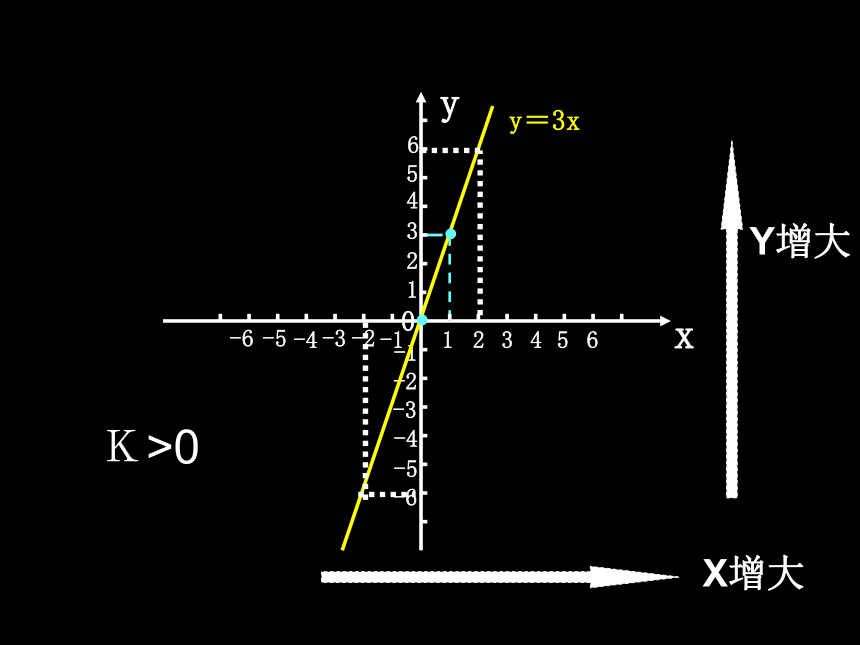
文档简介
课件27张PPT。2019年3月14日星期四深圳市福景外校
初二数学备课组 温故知新:1.作一次函数图象的步骤是什么?
列表,描点,连线。
2.一次函数y = kx + b(或y=kx)(k≠0)的图象是什么图形?
3:你至少通过确定几个点来作一次函数y=kx+b(或y=kx) (k≠0)的图象的呢?
图象是一条直线;两个点。
知识探究1:
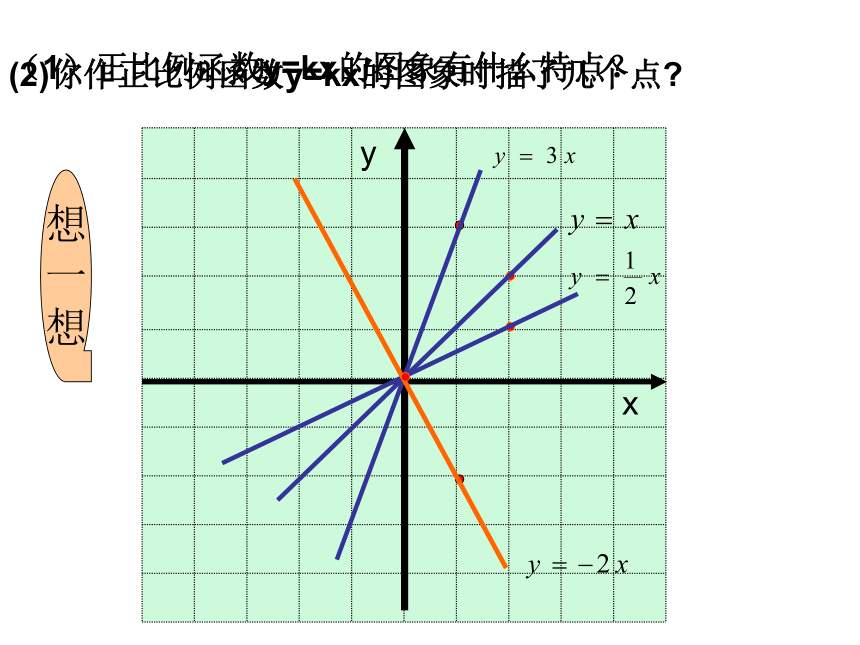
正比例函数的性质 在同一直角坐标系内作出正比例函数 的图象。做一做1(1)正比例函数y=kx的图象有什么特点?
(2)你作正比例函数y=kx的图象时描了几个点?想
一
想想
一
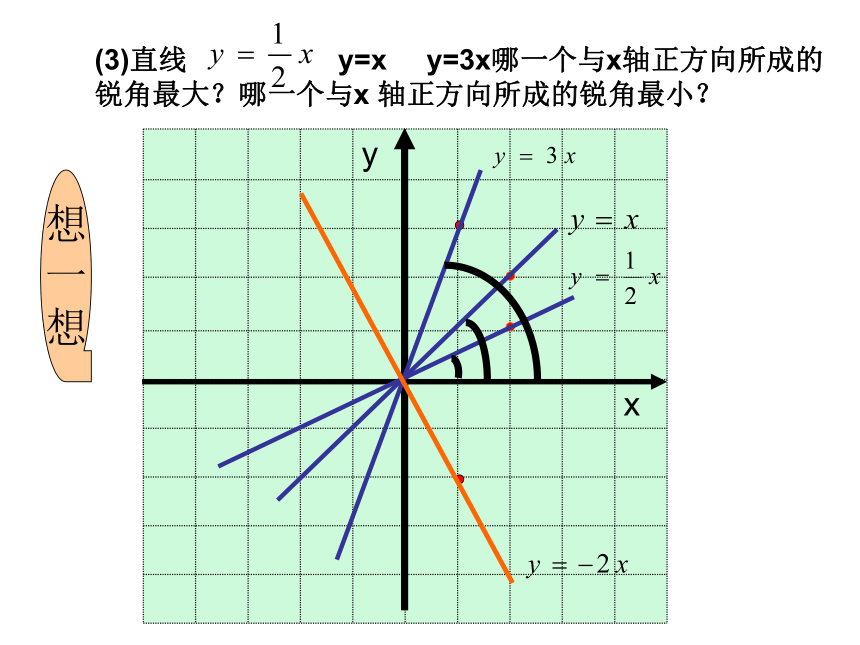
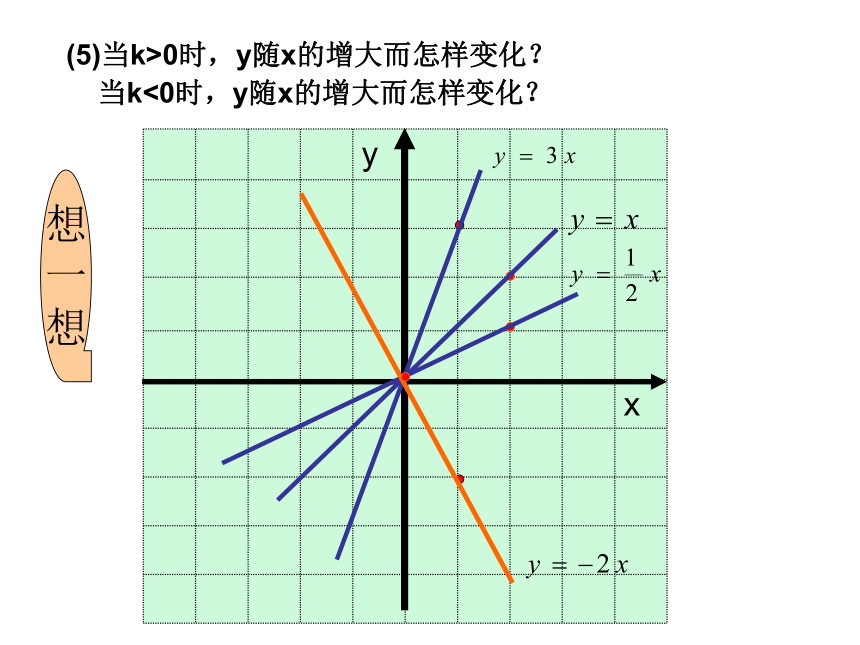
想(3)直线 y=x y=3x哪一个与x轴正方向所成的锐角最大?哪一个与x 轴正方向所成的锐角最小? 想
一
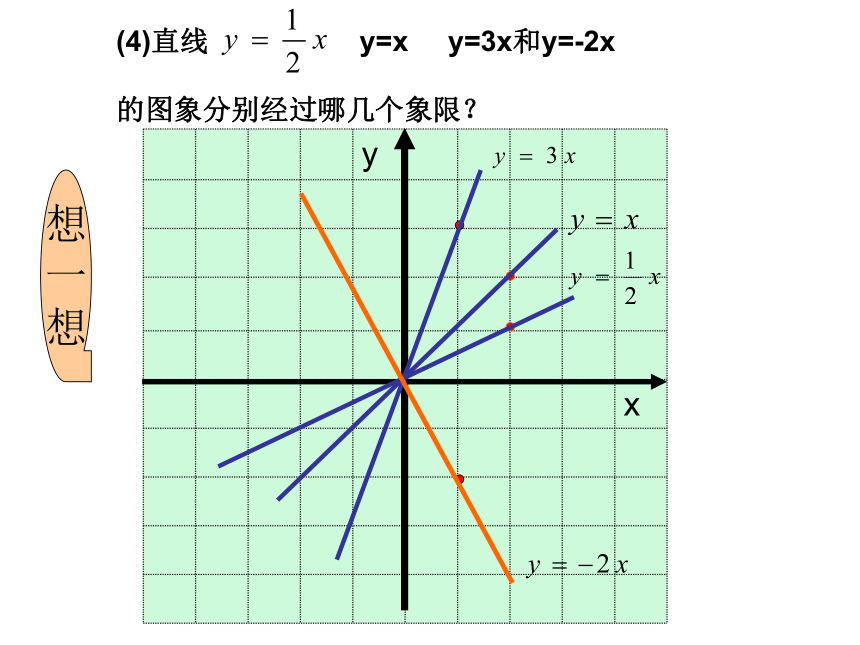
想(4)直线 y=x y=3x和y=-2x 的图象分别经过哪几个象限?想
一
想(5)当k>0时,y随x的增大而怎样变化?
当k<0时,y随x的增大而怎样变化?X增大Y增大K>0X增大Y减小1、正比例函数 y = kx 的图象都是经过坐标原点(0,0)的一条直线;
2.作正比例函数y=kx的图象时,除原点外,还需要找一点,一般找(1,k).
两点(0,0), (1, k) 确定直线y=kx.
3. 在正比例函数y=kx图象中,当k>0时,k的值越大,函数图象与x轴正方向所成的锐角越大
4. (1)当 k>0时,直线y=kx经过一、三象限,且y的值随x的值的增大而增大;
(2)当 k<0时,直线y=kx经过二、四象限,且y的值随x的值的增大而减小。
归纳总结:一、正比例函数y = kx (k≠0)图象的性质
知识探究2:
一次函数y=kx+b (k≠0)的图象的特点 在同一直角坐标系内分别作出一次函数y=x+4,y= -x,y= -x+4,y=5x的图象。做一做2议一议上述四个函数中,随着x值的增大,y的值分别如何变化?y=-x+4y=x+4y=5xy= - x0y-31y=x+41-222-13434155266377k>0图象呈上升趋势K>0时探索发现. . . . . . . . . . . . . . .. . . . . . . . . . . . . . .0yx-3y= - x+477-266-155441 33222311K<0时k<0图象呈下降趋势探索发现归纳总结:当k<0时,y的值随着x值的增大而减小,图象呈上升趋势;图象呈下降趋势。学 以 致 用1.下列函数,y的值随着x值的增大如何变化?增大减小增大减小想一想:(1)x从0开始逐渐增大时,y=2x+6和y=5x哪一个的值先达到20?这说明了什么?
(2)直线y=-x与y=-x+6的位置关系如何?
(3)直线y=2x+6与y=-x+6的位置关系如何?(1)x从0开始逐渐增大时,y=2x+6和y=5x哪一个的值先达到20?这说明了什么?y0x(5)当k的绝对值越大时,y随x的变化而变化得越快。反之也成立。(2)直线y=-x与y=-x+6的位置关系如何?y0x(3)直线y=2x+6与y=-x+6与的位置关系如何?
y0x想一想(1)x从0开始逐渐增大时,y=2x+6和y=5x哪一个的值先达到20?这说明了什么?
(2)直线y=-x和y=-x+6的位置关系如何?
(3)直线y=2x+6和y=-x+6的位置关系如何?答: y=5x的函数值先达到20,这说明随着x的增加,y=5x的函数值比y=2x+6的函数值增加得快。
答:平行(k相同,b不同)答:相交(k不相同),交点坐标是(0,6).(b=6相同)想一想!我的收获? y=kx
(k≠0) 一条直线
该直线经过(0,0),
(1,k)两点 当k<0时,图象经过第二、四象限,y随x的增大而减小y=kx+b
(k≠0) 该直线经过点(0,b),
当k>0时,y 随x 的增大而增大
当k<0时,y 随x 的增大而减小1.图象都经过原点2. 当k>0时,图象经过第一、三象限,y随x的增大而增大一条直线正比例
函数一次函数作业:P193 1.2.3.学习犹如采矿,你不动手,自然一无所获;
只要你动手就会采到晶莹的宝石。结束寄语
初二数学备课组 温故知新:1.作一次函数图象的步骤是什么?
列表,描点,连线。
2.一次函数y = kx + b(或y=kx)(k≠0)的图象是什么图形?
3:你至少通过确定几个点来作一次函数y=kx+b(或y=kx) (k≠0)的图象的呢?
图象是一条直线;两个点。
知识探究1:
正比例函数的性质 在同一直角坐标系内作出正比例函数 的图象。做一做1(1)正比例函数y=kx的图象有什么特点?
(2)你作正比例函数y=kx的图象时描了几个点?想
一
想想
一
想(3)直线 y=x y=3x哪一个与x轴正方向所成的锐角最大?哪一个与x 轴正方向所成的锐角最小? 想
一
想(4)直线 y=x y=3x和y=-2x 的图象分别经过哪几个象限?想
一
想(5)当k>0时,y随x的增大而怎样变化?
当k<0时,y随x的增大而怎样变化?X增大Y增大K>0X增大Y减小1、正比例函数 y = kx 的图象都是经过坐标原点(0,0)的一条直线;
2.作正比例函数y=kx的图象时,除原点外,还需要找一点,一般找(1,k).
两点(0,0), (1, k) 确定直线y=kx.
3. 在正比例函数y=kx图象中,当k>0时,k的值越大,函数图象与x轴正方向所成的锐角越大
4. (1)当 k>0时,直线y=kx经过一、三象限,且y的值随x的值的增大而增大;
(2)当 k<0时,直线y=kx经过二、四象限,且y的值随x的值的增大而减小。
归纳总结:一、正比例函数y = kx (k≠0)图象的性质
知识探究2:
一次函数y=kx+b (k≠0)的图象的特点 在同一直角坐标系内分别作出一次函数y=x+4,y= -x,y= -x+4,y=5x的图象。做一做2议一议上述四个函数中,随着x值的增大,y的值分别如何变化?y=-x+4y=x+4y=5xy= - x0y-31y=x+41-222-13434155266377k>0图象呈上升趋势K>0时探索发现. . . . . . . . . . . . . . .. . . . . . . . . . . . . . .0yx-3y= - x+477-266-155441 33222311K<0时k<0图象呈下降趋势探索发现归纳总结:当k<0时,y的值随着x值的增大而减小,图象呈上升趋势;图象呈下降趋势。学 以 致 用1.下列函数,y的值随着x值的增大如何变化?增大减小增大减小想一想:(1)x从0开始逐渐增大时,y=2x+6和y=5x哪一个的值先达到20?这说明了什么?
(2)直线y=-x与y=-x+6的位置关系如何?
(3)直线y=2x+6与y=-x+6的位置关系如何?(1)x从0开始逐渐增大时,y=2x+6和y=5x哪一个的值先达到20?这说明了什么?y0x(5)当k的绝对值越大时,y随x的变化而变化得越快。反之也成立。(2)直线y=-x与y=-x+6的位置关系如何?y0x(3)直线y=2x+6与y=-x+6与的位置关系如何?
y0x想一想(1)x从0开始逐渐增大时,y=2x+6和y=5x哪一个的值先达到20?这说明了什么?
(2)直线y=-x和y=-x+6的位置关系如何?
(3)直线y=2x+6和y=-x+6的位置关系如何?答: y=5x的函数值先达到20,这说明随着x的增加,y=5x的函数值比y=2x+6的函数值增加得快。
答:平行(k相同,b不同)答:相交(k不相同),交点坐标是(0,6).(b=6相同)想一想!我的收获? y=kx
(k≠0) 一条直线
该直线经过(0,0),
(1,k)两点 当k<0时,图象经过第二、四象限,y随x的增大而减小y=kx+b
(k≠0) 该直线经过点(0,b),
当k>0时,y 随x 的增大而增大
当k<0时,y 随x 的增大而减小1.图象都经过原点2. 当k>0时,图象经过第一、三象限,y随x的增大而增大一条直线正比例
函数一次函数作业:P193 1.2.3.学习犹如采矿,你不动手,自然一无所获;
只要你动手就会采到晶莹的宝石。结束寄语
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
