2.5.1直线与圆的位置关系 课件(共16张PPT)
文档属性
| 名称 | 2.5.1直线与圆的位置关系 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 12:21:05 | ||
图片预览






文档简介
(共16张PPT)
课时12 直线与圆的位置关系
新授课
1.能利用直线与圆位置关系解决实际问题.
导入:一个台风中心从A地以20km/h的速度向东北方向移动,离台风中心30km内的地区为危险区,城市B在A地正东40km处,则城市B处于危险区的时间为多长?
任务1:利用坐标法解决建筑的高度问题.
如图是某圆拱形桥一孔圆拱的示意图.圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m).
目标:能利用直线与圆位置关系解决实际问题.
解:建立如图所示的直角坐标系,使线段AB所在直线为x轴,O为坐标原点,圆心在y轴上.
由题意得,点P,B的坐标分别为(0,4),(10,0),设圆心坐标是(0,b),圆的半径是r,那么圆的方程是x2+(y-b)2=r2.
详解接下一页.
x
y
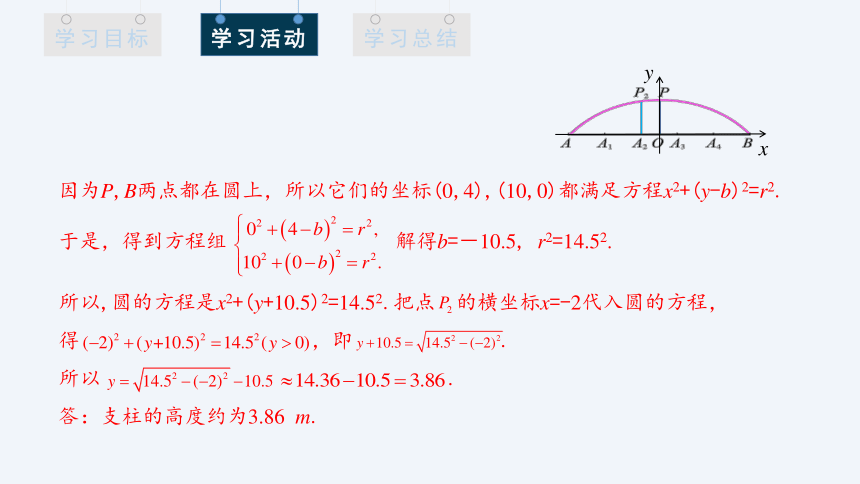
因为P,B两点都在圆上,所以它们的坐标(0,4),(10,0)都满足方程x2+(y-b)2=r2.于是,得到方程组 解得b=-10.5, r2=14.52.
所以,圆的方程是x2+(y+10.5)2=14.52.把点 的横坐标x=-2代入圆的方程,
得 ,即 .
所以 .
答:支柱的高度约为3.86 m.
x
y
思考1:结合上述的建系过程,讨论该如何建立合适的平面直角坐标系?
归纳总结
①若曲线是轴对称图形,则可选它的对称轴为坐标轴.
②常选特殊点作为直角坐标系的原点.
③尽量使已知点位于坐标轴上.
问题:如何利用综合法(几何法)求解该问题?
解:如图,过点 作 ,垂足为E,所以|OP|=4,
|OA|=10,点C为圆拱所在圆的圆心.
在Rt△AOC中,有 ,解得r=14.5.
在 中,有 ,因为 ,
所以 ,又因为OC=14.5-4=10.5,
于是 .
答:支柱的高度约为3.86 m.
思考2:比较上述两种方法,它们各自有什么特点?
坐标法:通过建立坐标系,将问题转化为代数问题,然后通过代数运算求解,方法具有普适性;
综合法(几何法):需要熟悉几何图形的性质,然后通过添加辅助线,运用垂径定理、勾股定理等有关性质定理计算求解,技巧性较高,不宜掌握.
任务2:利用直线与圆的位置关系判断航程安全问题.
一个小岛的周围有环岛暗礁,暗礁分布在以小岛中心为圆心,半径为20km的圆形区域内.已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处.如果轮船沿直线返港,那么它是否会有触礁危险?
问题1:结合已知,画出示意图,如何将其转化为数学问题?
如图, 根据题意,建立适当的平面直角坐标系,圆形区域表示暗礁所在区域,箭头表示轮船返港的路线,问题转化为利用方程判断直线与圆的位置关系,进而确定轮船是否有触礁危险.
问题2:轮船的航线与圆的位置关系是什么?
问题2:轮船的航线与圆的位置关系是什么?
解法1:以小岛的中心为原点O,东西方向为x轴,建立如图所示的直角坐标系,为了运算的简便,我们取10km为单位长度,则港口所在位置的坐标为(0,3),轮船所在位置的坐标为(4,0).
则暗礁所在圆形区域边缘对应圆O的方程为 ,其圆心坐标(0,0),半径为2;轮船航线所在直线l方程为 ,即 .联立直线与圆的方程,得 ,消去y,得 ,由 ,可知方程组无解.所以直线l与圆O相离,轮船沿直线返航不会有触礁危险.
解法2:在解法1的基础上,利用点到直线距求得圆形O到直线l的距离
,可知直线l与圆O相离,轮船沿直线返航不会有触礁危险.
解法3:如图过O做直线AB的垂线,设其长度为d.
由题可知AB=5,利用等面积法求得 ,因此直线l与圆O相离,轮船沿直线返航不会有触礁危险.
思考:结合任务1、任务2讨论如何利用坐标法解决平面几何问题?
归纳总结
坐标法解决平面几何问题基本步骤:
1.建立平面直角坐标系,用坐标和方程表示问题中的几何要素;
2.代数运算,得到相关代数结果;
3.把代数运算的结果“翻译”成几何结论.
练一练
一个台风中心从A地以20km/h的速度向东北方向移动,离台风中心30km内的地区为危险区,城市B在A地正东40km处,则城市B是否处于危险区,如果是,时长为多少?
以A地为坐标原点,AB所在直线为x轴,建立平面直角坐标系.
由题意可知,台风的轨迹为过A点,倾斜角为45°的直线l方程:y=x.以B(40,0)为圆心,30为半径的圆的方程为 ,所以圆心B到直线l的距离 ,所以城市B处于危险区,利用弦长公式可求得弦长为20,所以t=1.故城市B是否处于危险区,且时长为1h.
任务:回答下列问题,构建知识导图.
1.如何利用坐标法求解直线与圆的实际问题?
2.坐标法与综合法(几何法)在解决直线与圆的问题中的特点是什么?
课时12 直线与圆的位置关系
新授课
1.能利用直线与圆位置关系解决实际问题.
导入:一个台风中心从A地以20km/h的速度向东北方向移动,离台风中心30km内的地区为危险区,城市B在A地正东40km处,则城市B处于危险区的时间为多长?
任务1:利用坐标法解决建筑的高度问题.
如图是某圆拱形桥一孔圆拱的示意图.圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m).
目标:能利用直线与圆位置关系解决实际问题.
解:建立如图所示的直角坐标系,使线段AB所在直线为x轴,O为坐标原点,圆心在y轴上.
由题意得,点P,B的坐标分别为(0,4),(10,0),设圆心坐标是(0,b),圆的半径是r,那么圆的方程是x2+(y-b)2=r2.
详解接下一页.
x
y
因为P,B两点都在圆上,所以它们的坐标(0,4),(10,0)都满足方程x2+(y-b)2=r2.于是,得到方程组 解得b=-10.5, r2=14.52.
所以,圆的方程是x2+(y+10.5)2=14.52.把点 的横坐标x=-2代入圆的方程,
得 ,即 .
所以 .
答:支柱的高度约为3.86 m.
x
y
思考1:结合上述的建系过程,讨论该如何建立合适的平面直角坐标系?
归纳总结
①若曲线是轴对称图形,则可选它的对称轴为坐标轴.
②常选特殊点作为直角坐标系的原点.
③尽量使已知点位于坐标轴上.
问题:如何利用综合法(几何法)求解该问题?
解:如图,过点 作 ,垂足为E,所以|OP|=4,
|OA|=10,点C为圆拱所在圆的圆心.
在Rt△AOC中,有 ,解得r=14.5.
在 中,有 ,因为 ,
所以 ,又因为OC=14.5-4=10.5,
于是 .
答:支柱的高度约为3.86 m.
思考2:比较上述两种方法,它们各自有什么特点?
坐标法:通过建立坐标系,将问题转化为代数问题,然后通过代数运算求解,方法具有普适性;
综合法(几何法):需要熟悉几何图形的性质,然后通过添加辅助线,运用垂径定理、勾股定理等有关性质定理计算求解,技巧性较高,不宜掌握.
任务2:利用直线与圆的位置关系判断航程安全问题.
一个小岛的周围有环岛暗礁,暗礁分布在以小岛中心为圆心,半径为20km的圆形区域内.已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处.如果轮船沿直线返港,那么它是否会有触礁危险?
问题1:结合已知,画出示意图,如何将其转化为数学问题?
如图, 根据题意,建立适当的平面直角坐标系,圆形区域表示暗礁所在区域,箭头表示轮船返港的路线,问题转化为利用方程判断直线与圆的位置关系,进而确定轮船是否有触礁危险.
问题2:轮船的航线与圆的位置关系是什么?
问题2:轮船的航线与圆的位置关系是什么?
解法1:以小岛的中心为原点O,东西方向为x轴,建立如图所示的直角坐标系,为了运算的简便,我们取10km为单位长度,则港口所在位置的坐标为(0,3),轮船所在位置的坐标为(4,0).
则暗礁所在圆形区域边缘对应圆O的方程为 ,其圆心坐标(0,0),半径为2;轮船航线所在直线l方程为 ,即 .联立直线与圆的方程,得 ,消去y,得 ,由 ,可知方程组无解.所以直线l与圆O相离,轮船沿直线返航不会有触礁危险.
解法2:在解法1的基础上,利用点到直线距求得圆形O到直线l的距离
,可知直线l与圆O相离,轮船沿直线返航不会有触礁危险.
解法3:如图过O做直线AB的垂线,设其长度为d.
由题可知AB=5,利用等面积法求得 ,因此直线l与圆O相离,轮船沿直线返航不会有触礁危险.
思考:结合任务1、任务2讨论如何利用坐标法解决平面几何问题?
归纳总结
坐标法解决平面几何问题基本步骤:
1.建立平面直角坐标系,用坐标和方程表示问题中的几何要素;
2.代数运算,得到相关代数结果;
3.把代数运算的结果“翻译”成几何结论.
练一练
一个台风中心从A地以20km/h的速度向东北方向移动,离台风中心30km内的地区为危险区,城市B在A地正东40km处,则城市B是否处于危险区,如果是,时长为多少?
以A地为坐标原点,AB所在直线为x轴,建立平面直角坐标系.
由题意可知,台风的轨迹为过A点,倾斜角为45°的直线l方程:y=x.以B(40,0)为圆心,30为半径的圆的方程为 ,所以圆心B到直线l的距离 ,所以城市B处于危险区,利用弦长公式可求得弦长为20,所以t=1.故城市B是否处于危险区,且时长为1h.
任务:回答下列问题,构建知识导图.
1.如何利用坐标法求解直线与圆的实际问题?
2.坐标法与综合法(几何法)在解决直线与圆的问题中的特点是什么?
