1.4.2 用空间向量研究距离、夹角问题 课件(共20张PPT)
文档属性
| 名称 | 1.4.2 用空间向量研究距离、夹角问题 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-15 12:23:15 | ||
图片预览







文档简介
(共20张PPT)
课时10 用空间向量研究距离、夹角问题
新授课
1. 能利用投影向量推导出点到直线和点到平面的距离公式.
2. 能用向量方法解决点到直线、平行线间、点到平面、直线到平面(直线与平面平行)、平行平面间的距离问题.
任务1:复习回顾平面向量的投影向量.
目标一:能利用投影向量得到点到直线和点到平面的距离公式.
如图,在空间中任取一点,作 , .
1.怎样表示向量b方向上的单位向量u?
2.如何作出向量a在向量b方向上的投影向量?
3.怎样用单位向量u表示向量a在向量b方向上的投影向量及投影向量的模?
2.过点M作MM1垂直于直线ON,垂足为M1,向量 即为a在b方向上的投影向量.
3. ,即 , .
M1
任务2:探究利用向量求解空间点到已知直线的距离的方法.
已知直线l 的单位方向向量为u,A是直线l 上的定点,P是直线l 外一点,如何利用这些条件求点P到直线l的距离?
P
Q
l
A
u
如图,设 ,则向量 在直线l 上的投影向量
在 中,由勾股定理得点P到直线l的距离
(1)若AP与直线l 垂直,点P到直线l 的距离还等于 吗?
(2)在立体几何图形中求解距离的问题时,已知条件中一般只会给出点P以及直线l ,那么点P应该如何确定?
(3)求解距离的过程中是否需要确定垂线段的垂足?
(1)若AP与l 垂直,则 , .
(2)点到直线的距离,即点到直线的垂线段的长度不会随着点A的变化而变化,故点A可以是直线l上的任意一点.
(3)到直线的距离为参考向量的平方与投影向量的平方差的算术平方根.
因此,求解点P到直线l 距离问题时,只需直线l 的方向向量及l 上任意
一点A,这样得到参考向量 或 ,
再求得直线的单位方向向量,带入公式即可,因此不需要确定垂线段的垂足.
(4)求点到直线距离的主要有哪些方法?
归纳总结
求点到直线距离的方法:
1.作点到直线的垂线,点到垂足的距离即为点到直线的距离;
2.在三角形中用等面积法求解;
3.向量法,即点到直线的距离为参考向量的平方与投影向量的平方差的算术平方根.
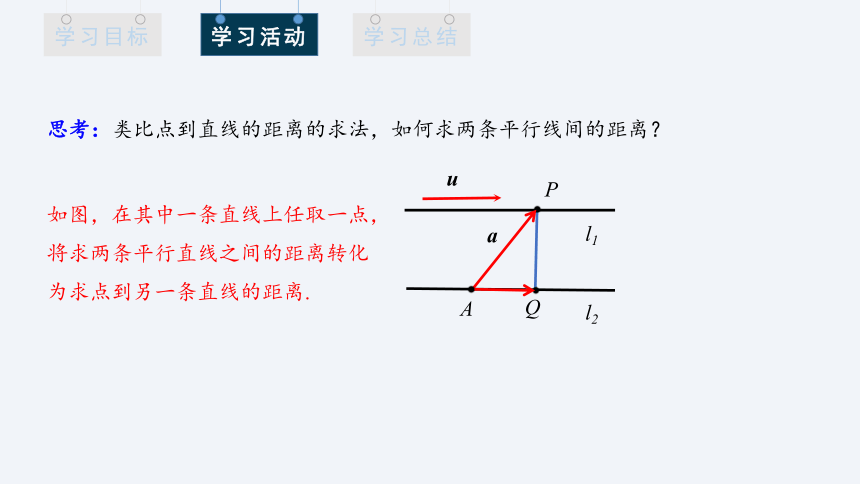
思考:类比点到直线的距离的求法,如何求两条平行线间的距离?
如图,在其中一条直线上任取一点,将求两条平行直线之间的距离转化为求点到另一条直线的距离.
l1
l2
u
A
P
Q
a
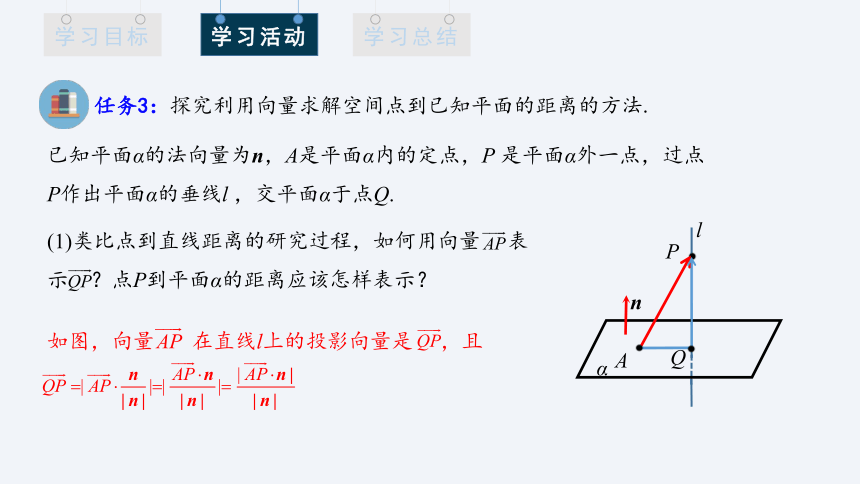
任务3:探究利用向量求解空间点到已知平面的距离的方法.
已知平面α的法向量为n,A是平面α内的定点,P 是平面α外一点,过点P作出平面α的垂线l ,交平面α于点Q.
(1)类比点到直线距离的研究过程,如何用向量 表示 ?点P到平面α的距离应该怎样表示?
如图,向量 在直线l上的投影向量是 ,且
l
P
Q
α
n
A
(2)在立体几何图形中求解距离的问题时,已知条件中一般只会给出点P及平面α,那点A该如何确定?求解距离的过程中是否需要找出点P在平面α内的投影及垂线段?
求解点P到平面α距离问题时,只需平面α的法向量及平面α内的任意一点A,这样得到“参考向量”,
明确点到平面的距离为参考向量与法向量数量积的绝对值与法向量的模之比,即参考向量与法向量方向上的单位向量的数量积取绝对值.
因此点A可以是平面α内任意一点,不需要找出点P在平面α内的投影及垂线段.
(3)求点到平面的距离主要有哪些方法?
归纳总结
求点到平面的距离的方法:
1.作点到平面的垂线,点与垂足的距离即为点到平面的距离.
2.在三棱锥中用等体积法求解.
3.向量法:点到平面的距离为参考向量与法向量数量积的绝对值与法向量的模之比.
思考:如果直线l与平面α平行,如何求直线与平面的距离?如何求两平行平面之间的距离?
证明直线与平面平行或面面平行,再转化为点到平面的距离.
目标二:能用向量方法解决点到直线、平行线间、点到平面、直线到平面(直线与平面平行)、平行平面间的距离问题.
任务:用向量方法求解空间中点到直线和平面的距离.
在棱长为1的正方体ABCD -A1B1C1D1 中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线 FC 到平面AEC1的距离.
解:以D1为原点,D1 A1,D1 C1,D1 D所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则A(1,0,1),B(1,1,1),C(0,1,1),C1(0,1,0),
所以
(1)取
则
所以,点B到直线AC1的距离为
设平面AEC1的法向量为n=(x,y,z),则
(2)因为 所以FC∥EC1,所以FC∥平面AEC1.
所以点F到平面AEC1的距离即为直线FC到平面AEC1的距离.
所以
取z=1,则x=1,y=2,所以n=(1,2,1)是平面AEC1的一个法向量.
,所以
又因为 所以点F到平面AEC1的距离为
即直线FC到平面AEC1的距离为
思考:上述过程中,求点到直线和点到平面两种距离的步骤是怎样的?
点P到直线l的距离:
1.建系,在直线l上任取一点A (注:选择特殊便于计算的点),求“参考向量 (或 )”的坐标.
2. 依据图形先求出直线l的单位方向向量u.
3.带入公式求解.
点P到平面α的距离:
1.建系,选择“参考向量” ;
2.确定平面α的法向量n;
3.带入公式求值.
归纳总结
1.建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
2.通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
3.把向量运算的结果“翻译”成相应的几何结论.
空间向量解决立体几何问题的 “三步曲”:
练一练
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,M为BB1的中点,N为BC的中点.
(1)求点M到直线AC1的距离;(2)求点N到平面MA1C1的距离.
解:(1)建立如图所示的空间直角坐标系,则A(0,0,0),A1(0,0,2),M(2,0,1),C1(0,2,2),
直线AC1的一个单位方向向量为 ,
故点M到直线AC1的距离为 .
(2)设平面MA1C1的一个法向量为 =(x,y,z),
则 ,即
取x=1,得z=2,
故 =(1,0,2)为平面MA1C1的一个法向量.
因为N(1,1,0),所以 =(-1,1,-1),
故N到平面MA1C1的距离
任务:回答下列问题,构建知识导图.
1.如何用向量法求空间中点到直线距离?
2.如何用向量法求空间中点到平面距离?
3.如何用空间向量解决立体几何问题?
课时10 用空间向量研究距离、夹角问题
新授课
1. 能利用投影向量推导出点到直线和点到平面的距离公式.
2. 能用向量方法解决点到直线、平行线间、点到平面、直线到平面(直线与平面平行)、平行平面间的距离问题.
任务1:复习回顾平面向量的投影向量.
目标一:能利用投影向量得到点到直线和点到平面的距离公式.
如图,在空间中任取一点,作 , .
1.怎样表示向量b方向上的单位向量u?
2.如何作出向量a在向量b方向上的投影向量?
3.怎样用单位向量u表示向量a在向量b方向上的投影向量及投影向量的模?
2.过点M作MM1垂直于直线ON,垂足为M1,向量 即为a在b方向上的投影向量.
3. ,即 , .
M1
任务2:探究利用向量求解空间点到已知直线的距离的方法.
已知直线l 的单位方向向量为u,A是直线l 上的定点,P是直线l 外一点,如何利用这些条件求点P到直线l的距离?
P
Q
l
A
u
如图,设 ,则向量 在直线l 上的投影向量
在 中,由勾股定理得点P到直线l的距离
(1)若AP与直线l 垂直,点P到直线l 的距离还等于 吗?
(2)在立体几何图形中求解距离的问题时,已知条件中一般只会给出点P以及直线l ,那么点P应该如何确定?
(3)求解距离的过程中是否需要确定垂线段的垂足?
(1)若AP与l 垂直,则 , .
(2)点到直线的距离,即点到直线的垂线段的长度不会随着点A的变化而变化,故点A可以是直线l上的任意一点.
(3)到直线的距离为参考向量的平方与投影向量的平方差的算术平方根.
因此,求解点P到直线l 距离问题时,只需直线l 的方向向量及l 上任意
一点A,这样得到参考向量 或 ,
再求得直线的单位方向向量,带入公式即可,因此不需要确定垂线段的垂足.
(4)求点到直线距离的主要有哪些方法?
归纳总结
求点到直线距离的方法:
1.作点到直线的垂线,点到垂足的距离即为点到直线的距离;
2.在三角形中用等面积法求解;
3.向量法,即点到直线的距离为参考向量的平方与投影向量的平方差的算术平方根.
思考:类比点到直线的距离的求法,如何求两条平行线间的距离?
如图,在其中一条直线上任取一点,将求两条平行直线之间的距离转化为求点到另一条直线的距离.
l1
l2
u
A
P
Q
a
任务3:探究利用向量求解空间点到已知平面的距离的方法.
已知平面α的法向量为n,A是平面α内的定点,P 是平面α外一点,过点P作出平面α的垂线l ,交平面α于点Q.
(1)类比点到直线距离的研究过程,如何用向量 表示 ?点P到平面α的距离应该怎样表示?
如图,向量 在直线l上的投影向量是 ,且
l
P
Q
α
n
A
(2)在立体几何图形中求解距离的问题时,已知条件中一般只会给出点P及平面α,那点A该如何确定?求解距离的过程中是否需要找出点P在平面α内的投影及垂线段?
求解点P到平面α距离问题时,只需平面α的法向量及平面α内的任意一点A,这样得到“参考向量”,
明确点到平面的距离为参考向量与法向量数量积的绝对值与法向量的模之比,即参考向量与法向量方向上的单位向量的数量积取绝对值.
因此点A可以是平面α内任意一点,不需要找出点P在平面α内的投影及垂线段.
(3)求点到平面的距离主要有哪些方法?
归纳总结
求点到平面的距离的方法:
1.作点到平面的垂线,点与垂足的距离即为点到平面的距离.
2.在三棱锥中用等体积法求解.
3.向量法:点到平面的距离为参考向量与法向量数量积的绝对值与法向量的模之比.
思考:如果直线l与平面α平行,如何求直线与平面的距离?如何求两平行平面之间的距离?
证明直线与平面平行或面面平行,再转化为点到平面的距离.
目标二:能用向量方法解决点到直线、平行线间、点到平面、直线到平面(直线与平面平行)、平行平面间的距离问题.
任务:用向量方法求解空间中点到直线和平面的距离.
在棱长为1的正方体ABCD -A1B1C1D1 中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线 FC 到平面AEC1的距离.
解:以D1为原点,D1 A1,D1 C1,D1 D所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则A(1,0,1),B(1,1,1),C(0,1,1),C1(0,1,0),
所以
(1)取
则
所以,点B到直线AC1的距离为
设平面AEC1的法向量为n=(x,y,z),则
(2)因为 所以FC∥EC1,所以FC∥平面AEC1.
所以点F到平面AEC1的距离即为直线FC到平面AEC1的距离.
所以
取z=1,则x=1,y=2,所以n=(1,2,1)是平面AEC1的一个法向量.
,所以
又因为 所以点F到平面AEC1的距离为
即直线FC到平面AEC1的距离为
思考:上述过程中,求点到直线和点到平面两种距离的步骤是怎样的?
点P到直线l的距离:
1.建系,在直线l上任取一点A (注:选择特殊便于计算的点),求“参考向量 (或 )”的坐标.
2. 依据图形先求出直线l的单位方向向量u.
3.带入公式求解.
点P到平面α的距离:
1.建系,选择“参考向量” ;
2.确定平面α的法向量n;
3.带入公式求值.
归纳总结
1.建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
2.通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
3.把向量运算的结果“翻译”成相应的几何结论.
空间向量解决立体几何问题的 “三步曲”:
练一练
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,M为BB1的中点,N为BC的中点.
(1)求点M到直线AC1的距离;(2)求点N到平面MA1C1的距离.
解:(1)建立如图所示的空间直角坐标系,则A(0,0,0),A1(0,0,2),M(2,0,1),C1(0,2,2),
直线AC1的一个单位方向向量为 ,
故点M到直线AC1的距离为 .
(2)设平面MA1C1的一个法向量为 =(x,y,z),
则 ,即
取x=1,得z=2,
故 =(1,0,2)为平面MA1C1的一个法向量.
因为N(1,1,0),所以 =(-1,1,-1),
故N到平面MA1C1的距离
任务:回答下列问题,构建知识导图.
1.如何用向量法求空间中点到直线距离?
2.如何用向量法求空间中点到平面距离?
3.如何用空间向量解决立体几何问题?
