2023—2024学年苏科版数学八年级上册期末模拟测试卷(无答案)
文档属性
| 名称 | 2023—2024学年苏科版数学八年级上册期末模拟测试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 289.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 13:36:23 | ||
图片预览



文档简介
2023-2024学年上学期八年级数学期末模拟测试卷(2)
一、选择题(本大题共10小题,每小题2分,共20分。在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是( )
A. B. C. D.
2.在平面直角坐标系中,点关于原点的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.用四舍五入法对数3465983取近似数精确到万位,结果是( )
A.347 B.3.46 C.3.47×106 D.3.46×107
4.如图,一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合,且与边AB、CD相交于G、H.将多边形OGBCH的面积记为S,三条线段GB、BC、CH的长度之和记为l,在大正六边形绕点O旋转过程中,下列说法正确的是( ).
A.S变化,l不变 B.S不变,l变化
C.S变化,l变化 D.S与l均不变
5.如图,直线和直线相交于点,则关于x,y的方程组,的解为( )
A. B.
C. D.
6.如图,直线y=kx+b与x轴交于点(﹣1,0),与y轴交于点(0,﹣2),则关于x的不等式kx+b<0的解集为( )
A.x>﹣1 B.x>﹣2 C.x<﹣1 D.x<﹣2
7.如图,△ABC中,AB=AC=8,BC=6,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是( )
A.7+ B.10 C.4+2 D.11
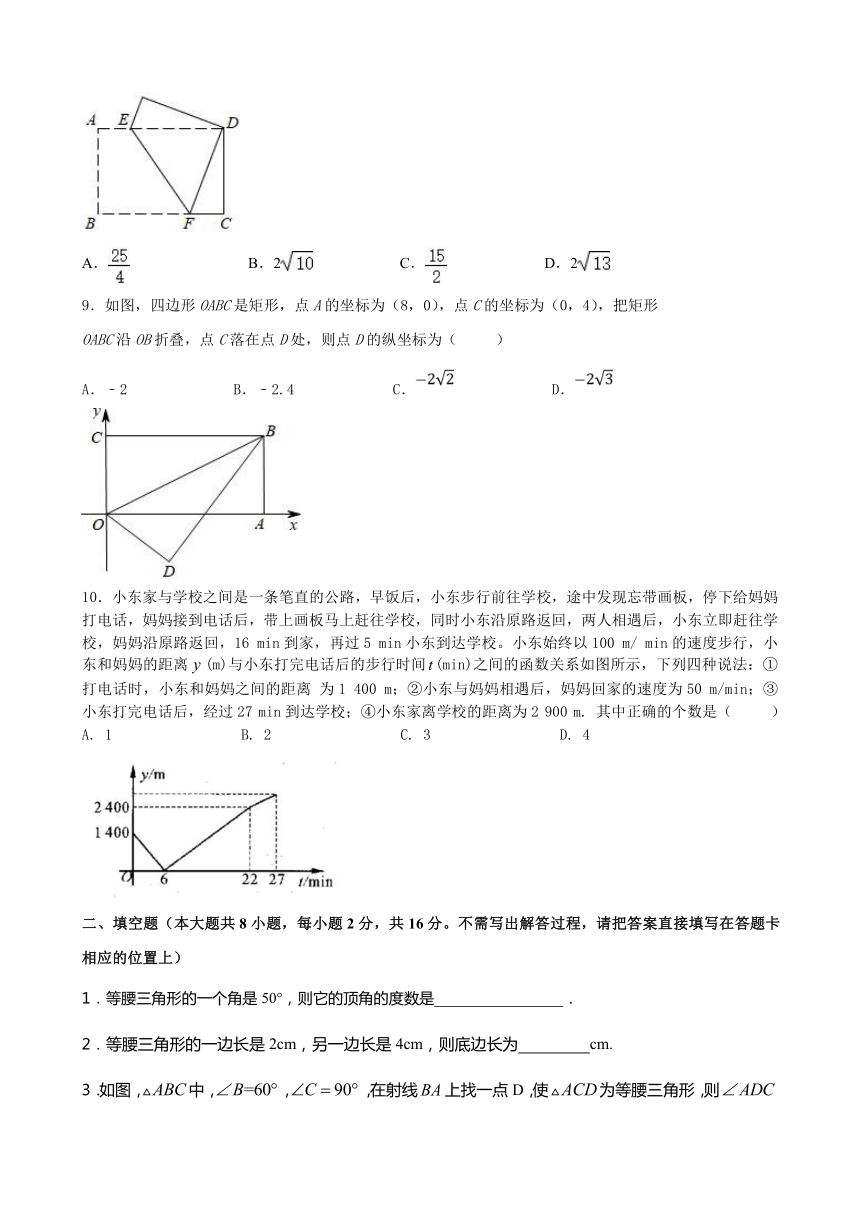
8.如图在矩形纸片ABCD中,AB=6,BC=8,将矩形纸片折叠,使点B与点D重合,则折痕EF的长是( )
A. B.2 C. D.2
9.如图,四边形OABC是矩形,点A的坐标为(8,0),点C的坐标为(0,4),把矩形
OABC沿OB折叠,点C落在点D处,则点D的纵坐标为( )
A.﹣2 B.﹣2.4 C. D.
10.小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回,16 min到家,再过5 min小东到达学校。小东始终以100 m/ min的速度步行,小东和妈妈的距离(m)与小东打完电话后的步行时间(min)之间的函数关系如图所示,下列四种说法:①打电话时,小东和妈妈之间的距离 为1 400 m;②小东与妈妈相遇后,妈妈回家的速度为50 m/min;③小东打完电话后,经过27 min到达学校;④小东家离学校的距离为2 900 m. 其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
二、填空题(本大题共8小题,每小题2分,共16分。不需写出解答过程,请把答案直接填写在答题卡相应的位置上)
1.等腰三角形的一个角是50°,则它的顶角的度数是 .
2.等腰三角形的一边长是2cm,另一边长是4cm,则底边长为 cm.
3.如图,中,,,在射线上找一点D,使为等腰三角形,则的度数为 .
4.如图,AD是△ABC的角平分线,若AB=2AC,则S△ABD∶S△ACD=
5.若直线不经过第一象限,则______(填“”、“”、“”)
6 如图,在中,,,是的角平分线,过点作,交的延长线于点若,则的长为 .
7. 在中,,,要使满足条件的唯一确定,那么边的长的取值范围是 .
8. 如图,在中,,,垂足为,若是的中点,则的长为 .
三、解答题(本大题共10小题,共64分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
1(1)求x的值:(x+1)2﹣25=0;
(2)计算:.
2 求下列各式中的值:
.
3在平面直角坐标系中,一次函数的图像平行于直线,且经过点,与轴交于点.
求这个一次函数的表达式
设点在轴上,当时,求点的坐标.
4如图,为的中点,直线、分别经过点、,且,以点为圆心,长为半径画弧交直线于点,连接求证,直线垂直平分;
如图,平面内直线,且相邻两直线间距离相等,点、分别在直线、上,连接用圆规和无刻度的直尺在直线上求作一点,使线段最短两种工具分别只限使用一次,并保留作图痕迹
5如图,D为△ABC外一点,∠DAB=∠B,CD⊥AD,∠1=∠2,若AC=7,BC=4,求AD的长.
6.在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,点F,点M都在直线l上,且点E和点F关于点M对称,直线EA与直线OF交于点P.
(Ⅰ)若点M的坐标为(1,﹣1),
①当点F的坐标为(1,1)时,如图,求点P的坐标;
②当点F为直线l上的动点时,记点P(x,y),求y关于x的函数解析式.
(Ⅱ)若点M(1,m),点F(1,t),其中t≠0,过点P作PQ⊥l于点Q,当OQ=PQ时,试用含t的式子表示m.
7如图1,平面直角坐标系中,直线与、轴分别交于点、,直线经过点,并与轴交于点.
(1)求,两点的坐标及的值;
(2)如图2,动点从原点出发,以每秒1个单位长度的速度沿轴正方向运动,过点作轴的垂线,分别交直线,于点,.设点运动的时间为.
①点的坐标为______,点的坐标为______;(均用含的式子表示)
②点是线段上一点.当点在射线上时,探究是否存在某一时刻,使,若存在,求出此时的值,并直接写出此时为等腰三角形时点的坐标;若不存在,说明理由.
9.某县实施“村村通”工程中,决定在A,B两村之间修筑一条公路,甲、乙两个工程队分别从A,B两村同时开始修筑,施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.如图是甲、乙两个工程队所修道路长度(m)与修筑时间(天)之间的函数图像,请根据图像所提供的信息,解答下列问题:
(1)求乙工程队所修道路的长度(m)与修筑时间(天)之间的函数表达式;
(2)甲工程队前8天所修道路长度为 m,该公路的总长度为 m;
(3)若乙工程队不提前离开,求甲、乙两队完成任务的天数;
(4)甲、乙两工程队第 天时所修道路的长度相差80 m.
10.如图所示,直线AB交x轴于点,交y轴于点,且a、b满足.
(1)若于点H,AH交OB于点P.
①如图1,求证:
②如图2,连接OH,求证:;
(2)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过D作交x轴于N点,当M点在y轴正半轴上运动的过程中,的值是否发生改变?如发生改变,直接写出该值的变化范围;若不改变,直接写出该值.
一、选择题(本大题共10小题,每小题2分,共20分。在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是( )
A. B. C. D.
2.在平面直角坐标系中,点关于原点的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.用四舍五入法对数3465983取近似数精确到万位,结果是( )
A.347 B.3.46 C.3.47×106 D.3.46×107
4.如图,一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合,且与边AB、CD相交于G、H.将多边形OGBCH的面积记为S,三条线段GB、BC、CH的长度之和记为l,在大正六边形绕点O旋转过程中,下列说法正确的是( ).
A.S变化,l不变 B.S不变,l变化
C.S变化,l变化 D.S与l均不变
5.如图,直线和直线相交于点,则关于x,y的方程组,的解为( )
A. B.
C. D.
6.如图,直线y=kx+b与x轴交于点(﹣1,0),与y轴交于点(0,﹣2),则关于x的不等式kx+b<0的解集为( )
A.x>﹣1 B.x>﹣2 C.x<﹣1 D.x<﹣2
7.如图,△ABC中,AB=AC=8,BC=6,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是( )
A.7+ B.10 C.4+2 D.11
8.如图在矩形纸片ABCD中,AB=6,BC=8,将矩形纸片折叠,使点B与点D重合,则折痕EF的长是( )
A. B.2 C. D.2
9.如图,四边形OABC是矩形,点A的坐标为(8,0),点C的坐标为(0,4),把矩形
OABC沿OB折叠,点C落在点D处,则点D的纵坐标为( )
A.﹣2 B.﹣2.4 C. D.
10.小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回,16 min到家,再过5 min小东到达学校。小东始终以100 m/ min的速度步行,小东和妈妈的距离(m)与小东打完电话后的步行时间(min)之间的函数关系如图所示,下列四种说法:①打电话时,小东和妈妈之间的距离 为1 400 m;②小东与妈妈相遇后,妈妈回家的速度为50 m/min;③小东打完电话后,经过27 min到达学校;④小东家离学校的距离为2 900 m. 其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
二、填空题(本大题共8小题,每小题2分,共16分。不需写出解答过程,请把答案直接填写在答题卡相应的位置上)
1.等腰三角形的一个角是50°,则它的顶角的度数是 .
2.等腰三角形的一边长是2cm,另一边长是4cm,则底边长为 cm.
3.如图,中,,,在射线上找一点D,使为等腰三角形,则的度数为 .
4.如图,AD是△ABC的角平分线,若AB=2AC,则S△ABD∶S△ACD=
5.若直线不经过第一象限,则______(填“”、“”、“”)
6 如图,在中,,,是的角平分线,过点作,交的延长线于点若,则的长为 .
7. 在中,,,要使满足条件的唯一确定,那么边的长的取值范围是 .
8. 如图,在中,,,垂足为,若是的中点,则的长为 .
三、解答题(本大题共10小题,共64分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
1(1)求x的值:(x+1)2﹣25=0;
(2)计算:.
2 求下列各式中的值:
.
3在平面直角坐标系中,一次函数的图像平行于直线,且经过点,与轴交于点.
求这个一次函数的表达式
设点在轴上,当时,求点的坐标.
4如图,为的中点,直线、分别经过点、,且,以点为圆心,长为半径画弧交直线于点,连接求证,直线垂直平分;
如图,平面内直线,且相邻两直线间距离相等,点、分别在直线、上,连接用圆规和无刻度的直尺在直线上求作一点,使线段最短两种工具分别只限使用一次,并保留作图痕迹
5如图,D为△ABC外一点,∠DAB=∠B,CD⊥AD,∠1=∠2,若AC=7,BC=4,求AD的长.
6.在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,点F,点M都在直线l上,且点E和点F关于点M对称,直线EA与直线OF交于点P.
(Ⅰ)若点M的坐标为(1,﹣1),
①当点F的坐标为(1,1)时,如图,求点P的坐标;
②当点F为直线l上的动点时,记点P(x,y),求y关于x的函数解析式.
(Ⅱ)若点M(1,m),点F(1,t),其中t≠0,过点P作PQ⊥l于点Q,当OQ=PQ时,试用含t的式子表示m.
7如图1,平面直角坐标系中,直线与、轴分别交于点、,直线经过点,并与轴交于点.
(1)求,两点的坐标及的值;
(2)如图2,动点从原点出发,以每秒1个单位长度的速度沿轴正方向运动,过点作轴的垂线,分别交直线,于点,.设点运动的时间为.
①点的坐标为______,点的坐标为______;(均用含的式子表示)
②点是线段上一点.当点在射线上时,探究是否存在某一时刻,使,若存在,求出此时的值,并直接写出此时为等腰三角形时点的坐标;若不存在,说明理由.
9.某县实施“村村通”工程中,决定在A,B两村之间修筑一条公路,甲、乙两个工程队分别从A,B两村同时开始修筑,施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.如图是甲、乙两个工程队所修道路长度(m)与修筑时间(天)之间的函数图像,请根据图像所提供的信息,解答下列问题:
(1)求乙工程队所修道路的长度(m)与修筑时间(天)之间的函数表达式;
(2)甲工程队前8天所修道路长度为 m,该公路的总长度为 m;
(3)若乙工程队不提前离开,求甲、乙两队完成任务的天数;
(4)甲、乙两工程队第 天时所修道路的长度相差80 m.
10.如图所示,直线AB交x轴于点,交y轴于点,且a、b满足.
(1)若于点H,AH交OB于点P.
①如图1,求证:
②如图2,连接OH,求证:;
(2)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过D作交x轴于N点,当M点在y轴正半轴上运动的过程中,的值是否发生改变?如发生改变,直接写出该值的变化范围;若不改变,直接写出该值.
同课章节目录
