第十三章 轴对称 三角形中的动点问题综合专题 教案 2023--2024学年人教版八年级数学上册
文档属性
| 名称 | 第十三章 轴对称 三角形中的动点问题综合专题 教案 2023--2024学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 461.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 13:39:20 | ||
图片预览

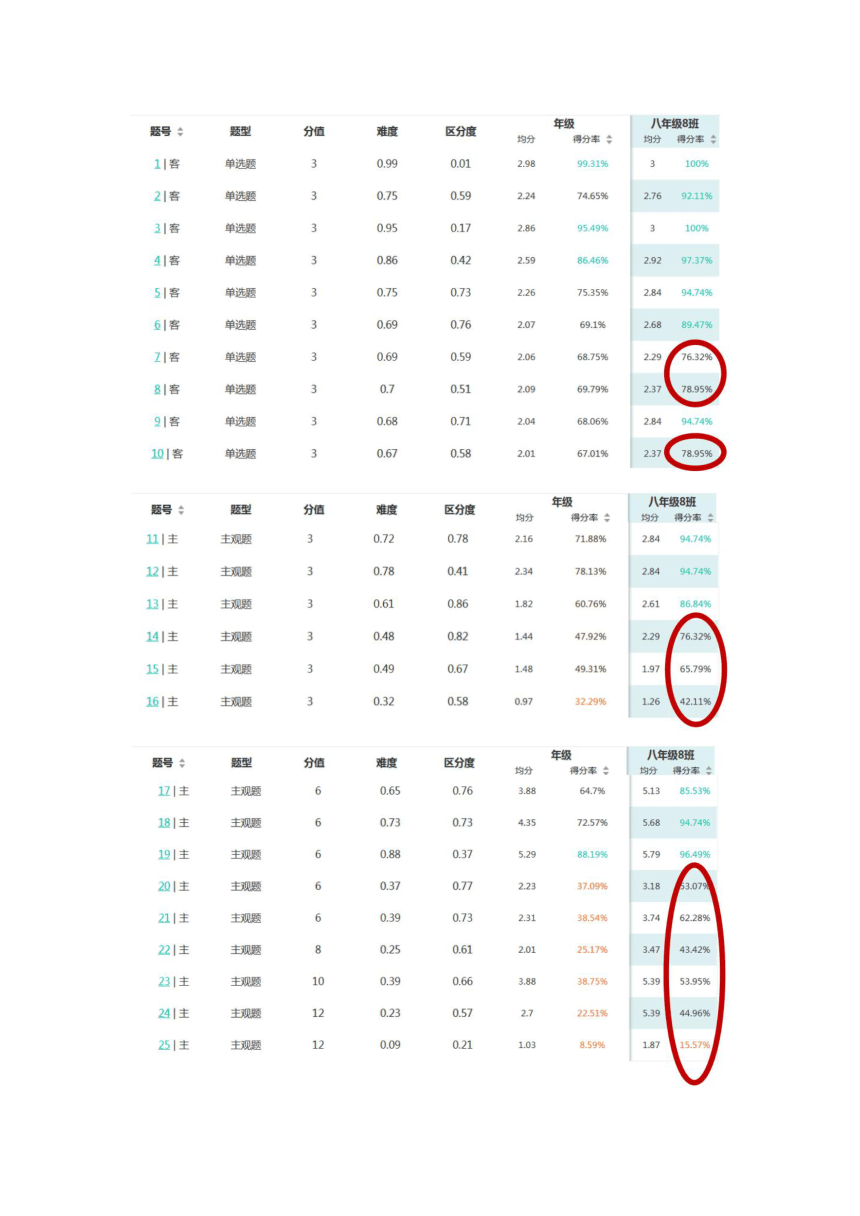
文档简介
三角形中的动点问题综合专题 教学设计
——综合练习讲评课
主讲老师:张艺 班级:初二(8)班 日期:2023年12月15日
学情分析
动点问题在初中数学中虽然没有编入课本,但却是习题中的常见形式,是数学试题的热点和命题的动向,也是初中学生学习数学中的一大难点。从数学思想的层面上讲,涉及以下思想:(1)运动观点;(2)方程思想;(3)数形结合思想;(4)分类思想:(5)转化思想等。
此次综合练习中,选择题、填空题和解答题这三大题型,都有涉及到三角形中的动点问题,因此,很有必要将此作为一个综合专题进行巩固,这样能够更好地帮助学生提升几何动态问题,扩展学生的思维。
教学目标
更正综合练习中的难题和高频错题,通过变式题目的练习,掌握同类型题目的解题思路和方法;
体验动点在三角形问题之中的运动和变化过程,分析这个过程中的数量关系、图形位置,结合三角形的性质和类型特点解决;
探究分类思想、数形结合思想和化归思想在动点问题中的运用,化动为静,提升学生的思维实力,激发思维踊跃性。
重难点
重点:分析动点运动改变过程中的数量关系、图形位置关系;
难点:将动点问题化动为静、数形结合、分类进行讨论。
教学过程
精准导向
分析此次综合练习的数据,将错误率较高的题目抽出来讲评,重点进行分析,类比变式题目来巩固,借此来总结方法。
合作探究
动点问题:由点运动产生的几何问题。
一般解决方法:1.研究背景图形, 标注 ;
2.分析 运动过程 ,画图; (目的:化动为静)
3.表达线段长,建 关系等式 .
深度攻坚
类型一.三角形中最短路径模型与动点问题
例题1.(对应于综合练习填空题第16题)如图,等腰△ABC的底边BC长为8,面积为24,腰AB的垂直平分线EF分别交AB,AC于点E,F,若点D为底边BC的中点,点M为线段EF上一动点,则BM+DM的最小值是 .
!小结:最短路径关键在于——找到两点( 两定点 )与“河”( 点运动的线段 ).
变式1.如图,在△ABC中,AB=AC,BC=4,△ABC的面积是16,AC的垂直平分线EF分别交AC,AB边于E,F两点.若D为BC边的中点,M为线段EF上一动点,求△CDM周长的最小值.
类型二.全等三角形与动点问题
例2.(对应于综合练习选择题第10题)如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,设运动时间为t(s),则当△ACP与△BPQ全等时,点Q的运动速度为( )
cm/s B.1cm/s或cm/s C.cm/s或2cm/s D.2cm/s
!小结:两三角形全等,先 找准 必定对应的对应点,再探讨不定对应点的情况( 分类讨论 ).
变式2.已知:如图,正方形ABCD的边长为10 cm,点E在边AB上,且AE=4 cm,点P在线段BC上以每秒2 cm的速度由点B向点C运动,同时点Q在线段CD上由点C向点D运动.设点P运动时间为t秒,若某一时刻△BPE与△CQP全等,求此时t的值及点Q的运动速度.
类型三.判断三角形类型与动点问题
例3.(对应于综合练习解答题第24题)如图,△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动.
(1)当点P的运动速度是1cm/s,点Q的运动速度是2cm/s,当Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),当t=2时,判断△BPQ的形状,并说明理由;
(2)当它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),则当t为何值时,△PBQ是直角三角形?
!小结:画出题中要求类型的三角形图形,用 整式 表示线段长度,根据三角形的特点列出 关系等式 ,解出后要 检验 .
变式3.如图,在△ABC中,AB=BC=AC=12 cm,现有两点M,N分别从点A,B同时出发,沿三角形的边顺时针运动,已知点M的速度为1 cm/s,点N的速度为2 cm/s.当点N回到点B时,M,N同时停止运动.
(1)点M,N运动几秒后,M,N两点重合?
(2)点M,N运动几秒后,可得到等边三角形AMN
(3)当点M,N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如果能,请求出此时M,N运动的时间.
增值评价
对于这节课,你还有什么疑问吗?
课后提升
1.如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,的度数是 .
2.如图,在长方形ABCD中,AB=DC=4,AD=BC=5.延长BC到E,使CE=2,连接DE.动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P运动时间为t秒.
(1)请用含t的式子表达△ABP的面积S.
(2)是否存在某个t值,使得△DCP和△DCE全等?若存在,请求出所有满足条件的t值;若不存在,请说明理由.
——综合练习讲评课
主讲老师:张艺 班级:初二(8)班 日期:2023年12月15日
学情分析
动点问题在初中数学中虽然没有编入课本,但却是习题中的常见形式,是数学试题的热点和命题的动向,也是初中学生学习数学中的一大难点。从数学思想的层面上讲,涉及以下思想:(1)运动观点;(2)方程思想;(3)数形结合思想;(4)分类思想:(5)转化思想等。
此次综合练习中,选择题、填空题和解答题这三大题型,都有涉及到三角形中的动点问题,因此,很有必要将此作为一个综合专题进行巩固,这样能够更好地帮助学生提升几何动态问题,扩展学生的思维。
教学目标
更正综合练习中的难题和高频错题,通过变式题目的练习,掌握同类型题目的解题思路和方法;
体验动点在三角形问题之中的运动和变化过程,分析这个过程中的数量关系、图形位置,结合三角形的性质和类型特点解决;
探究分类思想、数形结合思想和化归思想在动点问题中的运用,化动为静,提升学生的思维实力,激发思维踊跃性。
重难点
重点:分析动点运动改变过程中的数量关系、图形位置关系;
难点:将动点问题化动为静、数形结合、分类进行讨论。
教学过程
精准导向
分析此次综合练习的数据,将错误率较高的题目抽出来讲评,重点进行分析,类比变式题目来巩固,借此来总结方法。
合作探究
动点问题:由点运动产生的几何问题。
一般解决方法:1.研究背景图形, 标注 ;
2.分析 运动过程 ,画图; (目的:化动为静)
3.表达线段长,建 关系等式 .
深度攻坚
类型一.三角形中最短路径模型与动点问题
例题1.(对应于综合练习填空题第16题)如图,等腰△ABC的底边BC长为8,面积为24,腰AB的垂直平分线EF分别交AB,AC于点E,F,若点D为底边BC的中点,点M为线段EF上一动点,则BM+DM的最小值是 .
!小结:最短路径关键在于——找到两点( 两定点 )与“河”( 点运动的线段 ).
变式1.如图,在△ABC中,AB=AC,BC=4,△ABC的面积是16,AC的垂直平分线EF分别交AC,AB边于E,F两点.若D为BC边的中点,M为线段EF上一动点,求△CDM周长的最小值.
类型二.全等三角形与动点问题
例2.(对应于综合练习选择题第10题)如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,设运动时间为t(s),则当△ACP与△BPQ全等时,点Q的运动速度为( )
cm/s B.1cm/s或cm/s C.cm/s或2cm/s D.2cm/s
!小结:两三角形全等,先 找准 必定对应的对应点,再探讨不定对应点的情况( 分类讨论 ).
变式2.已知:如图,正方形ABCD的边长为10 cm,点E在边AB上,且AE=4 cm,点P在线段BC上以每秒2 cm的速度由点B向点C运动,同时点Q在线段CD上由点C向点D运动.设点P运动时间为t秒,若某一时刻△BPE与△CQP全等,求此时t的值及点Q的运动速度.
类型三.判断三角形类型与动点问题
例3.(对应于综合练习解答题第24题)如图,△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动.
(1)当点P的运动速度是1cm/s,点Q的运动速度是2cm/s,当Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),当t=2时,判断△BPQ的形状,并说明理由;
(2)当它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),则当t为何值时,△PBQ是直角三角形?
!小结:画出题中要求类型的三角形图形,用 整式 表示线段长度,根据三角形的特点列出 关系等式 ,解出后要 检验 .
变式3.如图,在△ABC中,AB=BC=AC=12 cm,现有两点M,N分别从点A,B同时出发,沿三角形的边顺时针运动,已知点M的速度为1 cm/s,点N的速度为2 cm/s.当点N回到点B时,M,N同时停止运动.
(1)点M,N运动几秒后,M,N两点重合?
(2)点M,N运动几秒后,可得到等边三角形AMN
(3)当点M,N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如果能,请求出此时M,N运动的时间.
增值评价
对于这节课,你还有什么疑问吗?
课后提升
1.如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,的度数是 .
2.如图,在长方形ABCD中,AB=DC=4,AD=BC=5.延长BC到E,使CE=2,连接DE.动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P运动时间为t秒.
(1)请用含t的式子表达△ABP的面积S.
(2)是否存在某个t值,使得△DCP和△DCE全等?若存在,请求出所有满足条件的t值;若不存在,请说明理由.
