2024年中考数学专题复习讲义—— 定义新运算题型之有理数(含答案)
文档属性
| 名称 | 2024年中考数学专题复习讲义—— 定义新运算题型之有理数(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 101.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 15:45:50 | ||
图片预览



文档简介
一(2) 定义新运算题型之有理数
★ 有理数 ★
【范例详解】
例1.(有理数)在古代,人们通过在绳子上打结来计数.即“结绳计数”.当时有位父亲为了准确记录孩子的出生天数,在粗细不同的绳子上打结(如图),由细到粗(右细左粗),满七进一,那么孩子已经出生了( )
A. 1335天 B. 516天 C. 435天 D. 54天
【解析】本题考查了有理数的混合运算,理解“满七进一”是解题的关键.根据题意以及图形分析,根据满七进一,即可求解.
解:绳结表示的数为,故选B
【巩固练习】
1.某校园学子餐厅把WIFI密码做成了数学题,小亮在餐厅就餐时,思索了一会,输入密码,顺利地连接到了学子餐厅的网络,那么他输入的密码是___________.
2算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大的贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字如图:
数字形式 1 2 3 4 5 6 7 8 9
纵式 | || ||| |||| |||||
横式
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空.示例如图:,则表示的数是_______________.
3.公元前2000年左右,古巴比伦人使用的楔形文字中有两个符号(如图所示),一个钉头形代表1,一个尖头形代表10.在古巴比伦的记数系统中,人们使用的标记方法和我们当今使用的方法相同,最右边的数字代表个位,然后是十位,百位.根据符号记数的方法,右下图符号表示一个两位数,则这个两位数是___________
4.一种新运算,规定以下两种变换:
①②
按照以上变换有那么________.
5.已知符号“f”表示一种运算,它对一些数的运算如下:f(1)=1+,f(2)=1+,f(3)=1+,f(4)=1+……,
(1)利用以上运算的规律写出f(n)=_________(n为正整数);
(2)计算f(1)f(2)f(3)f(100)的值;
(3)计算f(1)f(2)f(3)f(n)的值;
6.生活中常用的十进制是用0~9这十个数字来表示数,满十进一,例:12=1×10+2,212=2×10×10+1×10+2;
计算机也常用十六进制来表示字符代码,它是用0~F来表示0~15,满十六进一,它与十进制对应的数如表:
十进制 0 1 2 … 8 9 10 11 12 13 14 15 16 17 …
十六进制 0 1 2 … 8 9 A B C D E F 10 11 …
例:十六进制2B对应十进制的数为2×16+11=43,10C对应十进制的数为1×16×16+0×16+12=268,那么十六进制中14E对应十进制的数为( )
A.28 B.62 C.238 D.334
7.智慧的中国古代先民发明了抽象的符号来表达丰富的含义.例如,符号“”有刚毅的含义,符号“”有愉快的含义.符号中的“”表示“阴”,“”表示“阳”,类似这样自上而下排成的三行符号还有其他的含义.所有这些三行符号中,每一行只有一个阴或一个阳,且出现阴、阳的可能性相同.
(1)所有这些三行符号共有______种;
(2)若随机画一个这样的三行符号,求“画出含有一个阴和两个阳的三行符号”的概率.
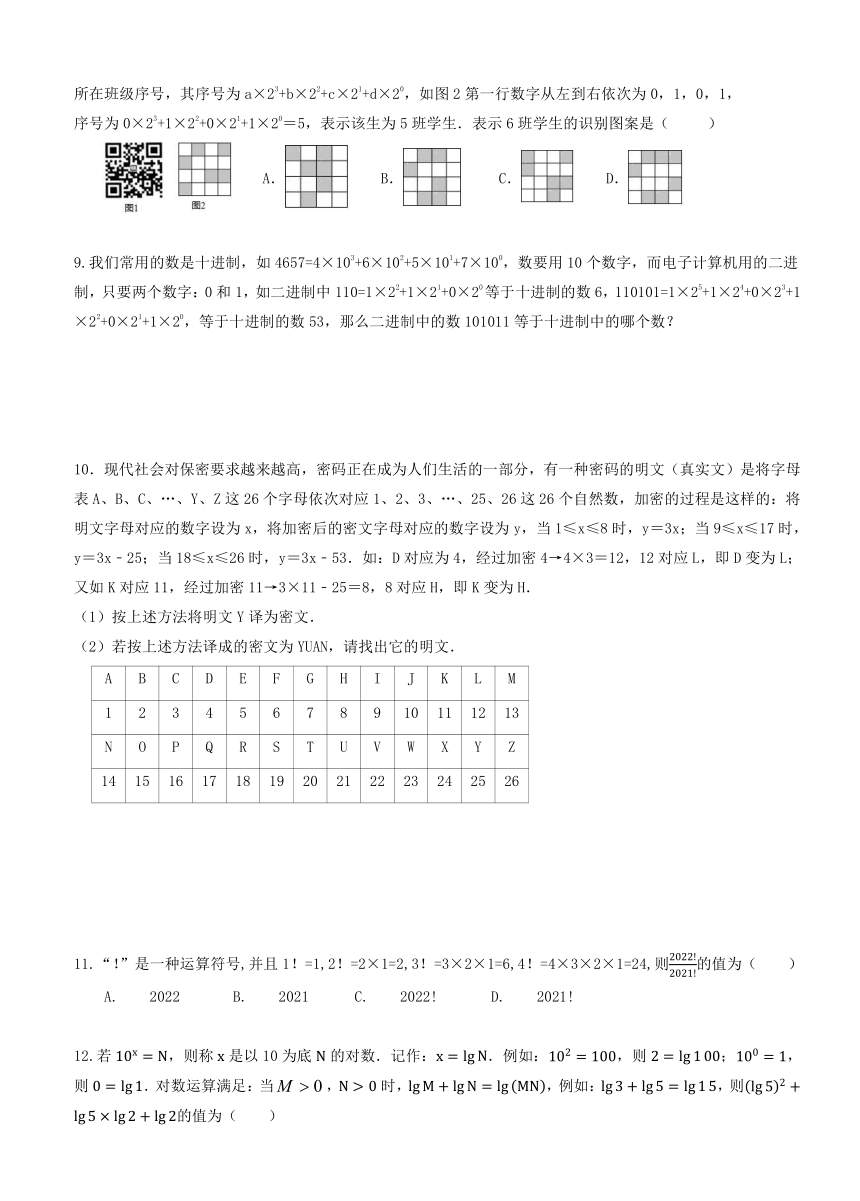
8.利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20,如图2第一行数字从左到右依次为0,1,0,1,
序号为0×23+1×22+0×21+1×20=5,表示该生为5班学生.表示6班学生的识别图案是( )
A. B. C. D.
9.我们常用的数是十进制,如4657=4×103+6×102+5×101+7×100,数要用10个数字,而电子计算机用的二进制,只要两个数字:0和1,如二进制中110=1×22+1×21+0×20等于十进制的数6,110101=1×25+1×24+0×23+1×22+0×21+1×20,等于十进制的数53,那么二进制中的数101011等于十进制中的哪个数?
10.现代社会对保密要求越来越高,密码正在成为人们生活的一部分,有一种密码的明文(真实文)是将字母
表A、B、C、…、Y、Z这26个字母依次对应1、2、3、…、25、26这26个自然数,加密的过程是这样的:将
明文字母对应的数字设为x,将加密后的密文字母对应的数字设为y,当1≤x≤8时,y=3x;当9≤x≤17时,
y=3x﹣25;当18≤x≤26时,y=3x﹣53.如:D对应为4,经过加密4→4×3=12,12对应L,即D变为L;
又如K对应11,经过加密11→3×11﹣25=8,8对应H,即K变为H.
(1)按上述方法将明文Y译为密文.
(2)若按上述方法译成的密文为YUAN,请找出它的明文.
A B C D E F G H I J K L M
1 2 3 4 5 6 7 8 9 10 11 12 13
N O P Q R S T U V W X Y Z
14 15 16 17 18 19 20 21 22 23 24 25 26
11.“!”是一种运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,则的值为( )
A. 2022 B. 2021 C. 2022! D. 2021!
12.若,则称是以10为底的对数.记作:.例如:,则;,则.对数运算满足:当,时,,例如:,则的值为( )
A. 5 B. 2 C. 1 D. 0
13.用符号M表示一种运算,它对整数和分数的运算结果分别如下:M(1)=-2,M(2)=-1,M(3)=0,M(4)=1……,M()=- ,M()=- ,M()=-……利用以上规律计算:(1)M(28)×M();(2)-1÷M(39)÷[-M()]
14.记Sn=a1,+a2+…an,令Tn=,则称Tn为a1,a2,…,an这列数的“凯森和”,已知a1,a2,…a500的“凯森和”为2004,那么1,a1,a2,…a500的“凯森和”为___________.
15.若正整数a,b,c(a<b<c)满足a2+b2=c2,则称(a,b,c)为一组“勾股数”.观察下列两类“勾股数”:
第一类(a是奇数):(3,4,5);(5,12,13);(7,24,25);…
第二类(a是偶数):(6,8,10);(8,15,17);(10,24,26);…
(1)请再写出两组勾股数,每类各写一组;
(2)分别就a为奇数、偶数两种情形,用a表示b和c,并选择其中一种情形证明(a,b,c)是“勾股数”.
16.定义:若10x=N,则x=log10N,x称为以10为底的N的对数,简记为lgN,其满足运算法则:
lgM+lgN=lg(M N)(M>0,N>0).例如:因为102=100,所以2=lg100,亦即lg100=2;lg4+lg3=lg12.
根据上述定义和运算法则,计算(lg2)2+lg2 lg5+lg5的结果为( )
A. 5 B. 2 C. 1 D. 0
17.我们根据对数的定义可得到对数的一个性质:,理由如下:设,则..由对数的定义得,又∵m+n=,∴ .
根据上述材料,结合你所学的知识,解答下列问题:
(1)填空:①___________;②____________,③=___________;
(2)求证:;
(3)拓展运用:计算.
18.定义一种运算,可以使a b=n(n为常数)时,得(a+1) b=n+3,a (b+1)=n-2,已知1 1=2,则2021 2022=___
19.规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2等,类比有理数的乘方,我们把2÷2÷2记作,读作“2的圈3次方”,又如(-3)÷(-3)÷(-3)÷(-3)记作,读作“-3的圈4次方”。请你阅读以上材料并完成下列问题:
(1)直接写出计算结果:=________;;
(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?仔细思考,将下列运算结果直接写成幂的形式. =________;=________;;
(3)计算:
20.已知x,y为有理数,现规定一种新运算“*”,满足x * y=x2y2-5.例如:1*2=12×22-5=-1.
(1)请计算下列各题:① 2 *(-3);②[(4*5)+5]*(- ).
(2)任意选择两个有理数,分别填入下列□和○中进行运算,并比较它们的运算结果的大小,则□*○________○*□(用“>”“<”或“=”填空).
【参考答案】
1.【解析】根据题中密码规律确定所求即可. 根据题意得出规律并熟练掌握运算法则是解题关键.
解:532=5×3×10000+5×2×100+5×(2+3)=151025
924=9×2×10000+9×4×100+9×(2+4)=183654,
863=8×6×10000+8×3×100+8×(3+6)=482472,
∴725=7×2×10000+7×5×100+7×(2+5)=143549.
2 【解析】理解算筹计数法,根据题中的新定义将所求的方程化为普通方程,整理后即可求出方程的解,即为x的值.解:根据算筹计数法,表示的数是:9167
3.【解析】理解题中的符号表示的意义是解题关键。
解:由题可知:十位上表示2个10,个位上表示5个1,所以这个两位数是25.
4.【解析】g[f(5,-6)]=g(5,6)=(-5,-6)
5.【解析】(1)f(n)= 1+;(2)原式=;
(3)原式=;
6.【解析】由题意得14E=1×16×16+4×16+14=334.故选:D.
7.【解析】(1)用列举法举出所有等可能的结果数即可;
(2)根据(1)列举的结果数和概率公式即可得出答案.
解:(1)共有8种等可能的情况数,分别是:阴,阴,阴;阴,阳,阴;阴,阴,阳;阳,阴,阴;阳,阳,阴;阳,阴,阳;阴,阳,阳;阳、阳、阳;故答案为:8;
(2)根据第(1)问一个阴、两个阳的共有3种,则有一个阴和两个阳的三行符号”的概率是.
8.【解析】根据规定的运算法则分别计算出每个选项第一行的数即可作出判断.
解:A、第一行数字从左到右依次为1、0、1、0,序号为1×23+0×22+1×21+0×20=10,不符合题意;
B、第一行数字从左到右依次为0,1,1,0,序号为0×23+1×22+1×21+0×20=6,符合题意;
C、第一行数字从左到右依次为1,0,0,1,序号为1×23+0×22+0×21+1×20=9,不符合题意;
D、第一行数字从左到右依次为0,1,1,1,序号为0×23+1×22+1×21+1×20=7,不符合题意;故选:B.
9.【解析】101011=1×25+0×24+1×23+0×22+1×21+1×20=32+0+8+0+2+1=43
10.【解析】(1)由表知“Y”对应的数字x=25,将其代入y=3x﹣53计算,再由表可得对应字母;
(2)先根据表格找到字母对应的数字,即y的值,找到合适的解析式求出对应的x的值,从而得出其对应的明文字母,据此可得.
解:(1)“Y”对应的数字x=25,则y=3×25﹣53=22,所以明文Y对应密文是V;
(2)Y对应数字为25,当3x﹣53=25时,x=26,对应明文为Z;
U对应数字为21,当2x=21时,x=7,对应明文为G;
A对应数字为1,当3x﹣53=1时,x=18,对应明文为R;
N对应数字为14,当3x﹣25=14时,x=13,对应明文为M;
所以密文为YUAN的对应明文为ZGRM.
11.【解析】,故选B.
12.【解析】通过阅读自定义运算规则:,再得到 再通过提取公因式后逐步进行运算即可得到答案.
解:,
故选C
13.【解析】(1)原式=(28-3)×[-()2]=25×(-)=-1
(2)原式=-1÷(39-3)÷{-[-()2]}=-1××36=-1
14.【解析】先根据已知求出T500的值,再设出新的凯森和Tx,列出式子,把得数代入,即可求出结果.
解:∵Tn=,∴T500=2004,设新的“凯森和”为Tx,501×Tx=1×501+500×T500,
Tx=(1×501+500×T500)÷501=(1×501+500×2004)÷501=1+500×4=2001.
15.【解析】本题考查了勾股数,读懂表格,从表格中获取有用信息进而发现规律是解题的关键.
(1)根据勾股数的定义即可得到结论;
(2)当a为奇数时,当a为偶数时,根据勾股数的定义即可得到结论.
解:(1)第一组(a是奇数):9,40,41(答案不唯一);第二组(a是偶数):12,35,37(答案不唯一);
(2)当a为奇数时,b=,c=;当a为偶数时,b=,c=;,;
证明:当a为奇数时,a2+b2=,∴(a,b,c)是“勾股数”.
当a为偶数时,a2+b2=,∴(a,b,c)是“勾股数“.”
16.【解答】(lg2)2+lg2 lg5+lg5=lg2(lg2+lg5)+lg5=lg2+lg5=1g10=1.故选:C.
17.【解析】(1)①∵,∴5,②∵,∴,③∵,∴=0;
(2)设logaM=m,logaN=n,∴,,∴,∴,
∴;
(3)=2
18.【解析】由定义可得2 1=2+3=5,2 2=5-2=3,3 2=3+3=6,3 3=6-2=4,4 4=5,5 5=6,∴2021 2021=2022,∴2021 2022=2022-2=2020
19.【解析】(1) =3÷3÷3÷3÷3÷3÷3÷3=;
(2) =5÷5÷5÷5÷5÷5÷5=;
=
(3)原式=
20.【解析】(1)①根据题中的新运算,得2*(-3)=22×(-3)2-5=36-5=31.
②根据题中的新运算,得
[(4*5 )+5]*(- )=(42×52-5+5)*(- )=400*(- )=4002×(- )2-5=- 5=
(2)可选0与1,则0*1=02×12-5=-5,1*0=12×02-5=-5,故答案是“=”
★ 有理数 ★
【范例详解】
例1.(有理数)在古代,人们通过在绳子上打结来计数.即“结绳计数”.当时有位父亲为了准确记录孩子的出生天数,在粗细不同的绳子上打结(如图),由细到粗(右细左粗),满七进一,那么孩子已经出生了( )
A. 1335天 B. 516天 C. 435天 D. 54天
【解析】本题考查了有理数的混合运算,理解“满七进一”是解题的关键.根据题意以及图形分析,根据满七进一,即可求解.
解:绳结表示的数为,故选B
【巩固练习】
1.某校园学子餐厅把WIFI密码做成了数学题,小亮在餐厅就餐时,思索了一会,输入密码,顺利地连接到了学子餐厅的网络,那么他输入的密码是___________.
2算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大的贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字如图:
数字形式 1 2 3 4 5 6 7 8 9
纵式 | || ||| |||| |||||
横式
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空.示例如图:,则表示的数是_______________.
3.公元前2000年左右,古巴比伦人使用的楔形文字中有两个符号(如图所示),一个钉头形代表1,一个尖头形代表10.在古巴比伦的记数系统中,人们使用的标记方法和我们当今使用的方法相同,最右边的数字代表个位,然后是十位,百位.根据符号记数的方法,右下图符号表示一个两位数,则这个两位数是___________
4.一种新运算,规定以下两种变换:
①②
按照以上变换有那么________.
5.已知符号“f”表示一种运算,它对一些数的运算如下:f(1)=1+,f(2)=1+,f(3)=1+,f(4)=1+……,
(1)利用以上运算的规律写出f(n)=_________(n为正整数);
(2)计算f(1)f(2)f(3)f(100)的值;
(3)计算f(1)f(2)f(3)f(n)的值;
6.生活中常用的十进制是用0~9这十个数字来表示数,满十进一,例:12=1×10+2,212=2×10×10+1×10+2;
计算机也常用十六进制来表示字符代码,它是用0~F来表示0~15,满十六进一,它与十进制对应的数如表:
十进制 0 1 2 … 8 9 10 11 12 13 14 15 16 17 …
十六进制 0 1 2 … 8 9 A B C D E F 10 11 …
例:十六进制2B对应十进制的数为2×16+11=43,10C对应十进制的数为1×16×16+0×16+12=268,那么十六进制中14E对应十进制的数为( )
A.28 B.62 C.238 D.334
7.智慧的中国古代先民发明了抽象的符号来表达丰富的含义.例如,符号“”有刚毅的含义,符号“”有愉快的含义.符号中的“”表示“阴”,“”表示“阳”,类似这样自上而下排成的三行符号还有其他的含义.所有这些三行符号中,每一行只有一个阴或一个阳,且出现阴、阳的可能性相同.
(1)所有这些三行符号共有______种;
(2)若随机画一个这样的三行符号,求“画出含有一个阴和两个阳的三行符号”的概率.
8.利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20,如图2第一行数字从左到右依次为0,1,0,1,
序号为0×23+1×22+0×21+1×20=5,表示该生为5班学生.表示6班学生的识别图案是( )
A. B. C. D.
9.我们常用的数是十进制,如4657=4×103+6×102+5×101+7×100,数要用10个数字,而电子计算机用的二进制,只要两个数字:0和1,如二进制中110=1×22+1×21+0×20等于十进制的数6,110101=1×25+1×24+0×23+1×22+0×21+1×20,等于十进制的数53,那么二进制中的数101011等于十进制中的哪个数?
10.现代社会对保密要求越来越高,密码正在成为人们生活的一部分,有一种密码的明文(真实文)是将字母
表A、B、C、…、Y、Z这26个字母依次对应1、2、3、…、25、26这26个自然数,加密的过程是这样的:将
明文字母对应的数字设为x,将加密后的密文字母对应的数字设为y,当1≤x≤8时,y=3x;当9≤x≤17时,
y=3x﹣25;当18≤x≤26时,y=3x﹣53.如:D对应为4,经过加密4→4×3=12,12对应L,即D变为L;
又如K对应11,经过加密11→3×11﹣25=8,8对应H,即K变为H.
(1)按上述方法将明文Y译为密文.
(2)若按上述方法译成的密文为YUAN,请找出它的明文.
A B C D E F G H I J K L M
1 2 3 4 5 6 7 8 9 10 11 12 13
N O P Q R S T U V W X Y Z
14 15 16 17 18 19 20 21 22 23 24 25 26
11.“!”是一种运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,则的值为( )
A. 2022 B. 2021 C. 2022! D. 2021!
12.若,则称是以10为底的对数.记作:.例如:,则;,则.对数运算满足:当,时,,例如:,则的值为( )
A. 5 B. 2 C. 1 D. 0
13.用符号M表示一种运算,它对整数和分数的运算结果分别如下:M(1)=-2,M(2)=-1,M(3)=0,M(4)=1……,M()=- ,M()=- ,M()=-……利用以上规律计算:(1)M(28)×M();(2)-1÷M(39)÷[-M()]
14.记Sn=a1,+a2+…an,令Tn=,则称Tn为a1,a2,…,an这列数的“凯森和”,已知a1,a2,…a500的“凯森和”为2004,那么1,a1,a2,…a500的“凯森和”为___________.
15.若正整数a,b,c(a<b<c)满足a2+b2=c2,则称(a,b,c)为一组“勾股数”.观察下列两类“勾股数”:
第一类(a是奇数):(3,4,5);(5,12,13);(7,24,25);…
第二类(a是偶数):(6,8,10);(8,15,17);(10,24,26);…
(1)请再写出两组勾股数,每类各写一组;
(2)分别就a为奇数、偶数两种情形,用a表示b和c,并选择其中一种情形证明(a,b,c)是“勾股数”.
16.定义:若10x=N,则x=log10N,x称为以10为底的N的对数,简记为lgN,其满足运算法则:
lgM+lgN=lg(M N)(M>0,N>0).例如:因为102=100,所以2=lg100,亦即lg100=2;lg4+lg3=lg12.
根据上述定义和运算法则,计算(lg2)2+lg2 lg5+lg5的结果为( )
A. 5 B. 2 C. 1 D. 0
17.我们根据对数的定义可得到对数的一个性质:,理由如下:设,则..由对数的定义得,又∵m+n=,∴ .
根据上述材料,结合你所学的知识,解答下列问题:
(1)填空:①___________;②____________,③=___________;
(2)求证:;
(3)拓展运用:计算.
18.定义一种运算,可以使a b=n(n为常数)时,得(a+1) b=n+3,a (b+1)=n-2,已知1 1=2,则2021 2022=___
19.规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2等,类比有理数的乘方,我们把2÷2÷2记作,读作“2的圈3次方”,又如(-3)÷(-3)÷(-3)÷(-3)记作,读作“-3的圈4次方”。请你阅读以上材料并完成下列问题:
(1)直接写出计算结果:=________;;
(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?仔细思考,将下列运算结果直接写成幂的形式. =________;=________;;
(3)计算:
20.已知x,y为有理数,现规定一种新运算“*”,满足x * y=x2y2-5.例如:1*2=12×22-5=-1.
(1)请计算下列各题:① 2 *(-3);②[(4*5)+5]*(- ).
(2)任意选择两个有理数,分别填入下列□和○中进行运算,并比较它们的运算结果的大小,则□*○________○*□(用“>”“<”或“=”填空).
【参考答案】
1.【解析】根据题中密码规律确定所求即可. 根据题意得出规律并熟练掌握运算法则是解题关键.
解:532=5×3×10000+5×2×100+5×(2+3)=151025
924=9×2×10000+9×4×100+9×(2+4)=183654,
863=8×6×10000+8×3×100+8×(3+6)=482472,
∴725=7×2×10000+7×5×100+7×(2+5)=143549.
2 【解析】理解算筹计数法,根据题中的新定义将所求的方程化为普通方程,整理后即可求出方程的解,即为x的值.解:根据算筹计数法,表示的数是:9167
3.【解析】理解题中的符号表示的意义是解题关键。
解:由题可知:十位上表示2个10,个位上表示5个1,所以这个两位数是25.
4.【解析】g[f(5,-6)]=g(5,6)=(-5,-6)
5.【解析】(1)f(n)= 1+;(2)原式=;
(3)原式=;
6.【解析】由题意得14E=1×16×16+4×16+14=334.故选:D.
7.【解析】(1)用列举法举出所有等可能的结果数即可;
(2)根据(1)列举的结果数和概率公式即可得出答案.
解:(1)共有8种等可能的情况数,分别是:阴,阴,阴;阴,阳,阴;阴,阴,阳;阳,阴,阴;阳,阳,阴;阳,阴,阳;阴,阳,阳;阳、阳、阳;故答案为:8;
(2)根据第(1)问一个阴、两个阳的共有3种,则有一个阴和两个阳的三行符号”的概率是.
8.【解析】根据规定的运算法则分别计算出每个选项第一行的数即可作出判断.
解:A、第一行数字从左到右依次为1、0、1、0,序号为1×23+0×22+1×21+0×20=10,不符合题意;
B、第一行数字从左到右依次为0,1,1,0,序号为0×23+1×22+1×21+0×20=6,符合题意;
C、第一行数字从左到右依次为1,0,0,1,序号为1×23+0×22+0×21+1×20=9,不符合题意;
D、第一行数字从左到右依次为0,1,1,1,序号为0×23+1×22+1×21+1×20=7,不符合题意;故选:B.
9.【解析】101011=1×25+0×24+1×23+0×22+1×21+1×20=32+0+8+0+2+1=43
10.【解析】(1)由表知“Y”对应的数字x=25,将其代入y=3x﹣53计算,再由表可得对应字母;
(2)先根据表格找到字母对应的数字,即y的值,找到合适的解析式求出对应的x的值,从而得出其对应的明文字母,据此可得.
解:(1)“Y”对应的数字x=25,则y=3×25﹣53=22,所以明文Y对应密文是V;
(2)Y对应数字为25,当3x﹣53=25时,x=26,对应明文为Z;
U对应数字为21,当2x=21时,x=7,对应明文为G;
A对应数字为1,当3x﹣53=1时,x=18,对应明文为R;
N对应数字为14,当3x﹣25=14时,x=13,对应明文为M;
所以密文为YUAN的对应明文为ZGRM.
11.【解析】,故选B.
12.【解析】通过阅读自定义运算规则:,再得到 再通过提取公因式后逐步进行运算即可得到答案.
解:,
故选C
13.【解析】(1)原式=(28-3)×[-()2]=25×(-)=-1
(2)原式=-1÷(39-3)÷{-[-()2]}=-1××36=-1
14.【解析】先根据已知求出T500的值,再设出新的凯森和Tx,列出式子,把得数代入,即可求出结果.
解:∵Tn=,∴T500=2004,设新的“凯森和”为Tx,501×Tx=1×501+500×T500,
Tx=(1×501+500×T500)÷501=(1×501+500×2004)÷501=1+500×4=2001.
15.【解析】本题考查了勾股数,读懂表格,从表格中获取有用信息进而发现规律是解题的关键.
(1)根据勾股数的定义即可得到结论;
(2)当a为奇数时,当a为偶数时,根据勾股数的定义即可得到结论.
解:(1)第一组(a是奇数):9,40,41(答案不唯一);第二组(a是偶数):12,35,37(答案不唯一);
(2)当a为奇数时,b=,c=;当a为偶数时,b=,c=;,;
证明:当a为奇数时,a2+b2=,∴(a,b,c)是“勾股数”.
当a为偶数时,a2+b2=,∴(a,b,c)是“勾股数“.”
16.【解答】(lg2)2+lg2 lg5+lg5=lg2(lg2+lg5)+lg5=lg2+lg5=1g10=1.故选:C.
17.【解析】(1)①∵,∴5,②∵,∴,③∵,∴=0;
(2)设logaM=m,logaN=n,∴,,∴,∴,
∴;
(3)=2
18.【解析】由定义可得2 1=2+3=5,2 2=5-2=3,3 2=3+3=6,3 3=6-2=4,4 4=5,5 5=6,∴2021 2021=2022,∴2021 2022=2022-2=2020
19.【解析】(1) =3÷3÷3÷3÷3÷3÷3÷3=;
(2) =5÷5÷5÷5÷5÷5÷5=;
=
(3)原式=
20.【解析】(1)①根据题中的新运算,得2*(-3)=22×(-3)2-5=36-5=31.
②根据题中的新运算,得
[(4*5 )+5]*(- )=(42×52-5+5)*(- )=400*(- )=4002×(- )2-5=- 5=
(2)可选0与1,则0*1=02×12-5=-5,1*0=12×02-5=-5,故答案是“=”
同课章节目录
