2023-2024学年江苏省九年级数学期末突击模拟卷04(含解析)
文档属性
| 名称 | 2023-2024学年江苏省九年级数学期末突击模拟卷04(含解析) |  | |
| 格式 | Doc | ||
| 文件大小 | 380.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 16:06:05 | ||
图片预览




文档简介
2023-2024学年江苏省九年级数学期末突击模拟卷04
一.选择题(共6小题)
1.若(m+4)x|m|﹣2﹣x﹣5=0是关于x的一元二次方程,则m的值为( )
A.4 B.﹣4 C.±4 D.±2
2.已知⊙O的直径为5,若PO=3,则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法判断
3.某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行综合考核(考核的满分均为100分),三个方面的重要性之比依次为3:5:2.小王经过考核后所得的各项分数依次为90、88、85分,那么小王的最后综合得分是( )
A.87 B.87.5 C.87.6 D.88
4.已知A(x1,y1)、B(x2,y2)为二次函数y=﹣(x﹣1)2+k图象上两点,且x1<x2<1,则下列说法正确的是( )
A.y1+y2>0 B.y1+y2<0 C.y1﹣y2>0 D.y1﹣y2<0
5.二次函数y=(x﹣1)2﹣2,若y随x的增大而增大,则x的取值范围是( )
A.x>1 B.x<1 C.x>﹣1 D.x<﹣1
6.如图,AB是⊙O的直径,CD是⊙O的切线,D为切点,AC⊥CD,垂足为C,连接BD.若AB=8,且∠B=30°,则CD的长为( )
A.2 B.2 C.4 D.4
二.填空题(共12小题)
7.已知某校学生“科技创新社团”成员的年龄与人数情况如下表所示:那么“科技创新社团”成员年龄的中位数是 岁.
年龄(岁) 11 12 13 14 15
人数 5 5 16 15 12
8.将抛物线y=2(x+4)2向右平移3个单位,得到新抛物线的表达式是 .
9.在一个不透明的袋中装有7个红球和3个白球,这些球除颜色外无其他差别,随机从袋中摸出一个球,这个球是白球的概率是 .
10.某店8月份利润为16万元,要使10月份利润达到25万元,设月平均增长率为x,根据题意可列方程 .
11.甲、乙两名同学5次数学考试的平均成绩都是102分,方差分别为S甲2=38,S乙2=10,则 同学的数学成绩更稳定.
12.弧长为8π半径为12的扇形,它的圆心角的度数是 .
13.抛物线y=x2+x不经过第 象限.
14.如图,AB是⊙O的弦,连接BO,作AC⊥BO交BO的延长线于点C,已知OC=,BO=2,点D是的中点,连接CD,则CD的长为 .
15.若m是方程2x2﹣3x﹣1=0的一个根,则6m2﹣9m+2023的值为 .
16.测量7名学生的体温(单位:℃)如下:36.5,36.3,36.8,36.3,36.5,36.7,36.5,这组数据的众数是 ℃.
17.抛物线y=ax2+bx+c(a≠0)的图象如图所示,抛物线经过点(﹣1,0),则下列结论:①abc<0;②2a﹣b>0;③3a+c>0;④a+b>am2+bm(m为一切实数);⑤b2>4ac;正确的是 (填写序号).
18.小球在如图所示的地板上自由地滚动,并最终随机地停留在某块方砖上(每块方砖除颜色外完全相同),则小球停留在黑色区域的概率是 .
三.解答题(共8小题)
19.用适当的方法解方程:
(1)x2+4x﹣2=0;
(2)2x2﹣3x+1=0.
20.为了缅怀先烈,向中国人民志愿军致敬,近两年涌现了很多抗美援朝的电影作品,《长津湖》和《狙击手》正是其中优秀的代表.为了解学生对这两部作品的评价,某调查小组从该学校观看过这两部电影的学生中各随机抽取了20名学生对这两部作品分别进行评分,并通过整理和分析,给出了部分信息.
抽取的学生对两部作品分别评分的平均数,众数和中位数:
平均数 众数 中位数
《长津湖》 8.2 9 b
《狙击手》 ﹣﹣﹣﹣ c 8
根据以上信息,解答下列问题:
(1)上述图表中的a= ,b= ,c= .
(2)求《狙击手》评分的平均数;
(3)若该校有1000名学生观看过这两部影片,若他们都对这两部作品进行评分,你认为这两部作品一共可得到多少个满分?
21.(1)解方程:3(x﹣2)2=2(x﹣2);
(2)将二次函数y=﹣x2﹣x+化为y=a(x﹣h)2+k的形式.
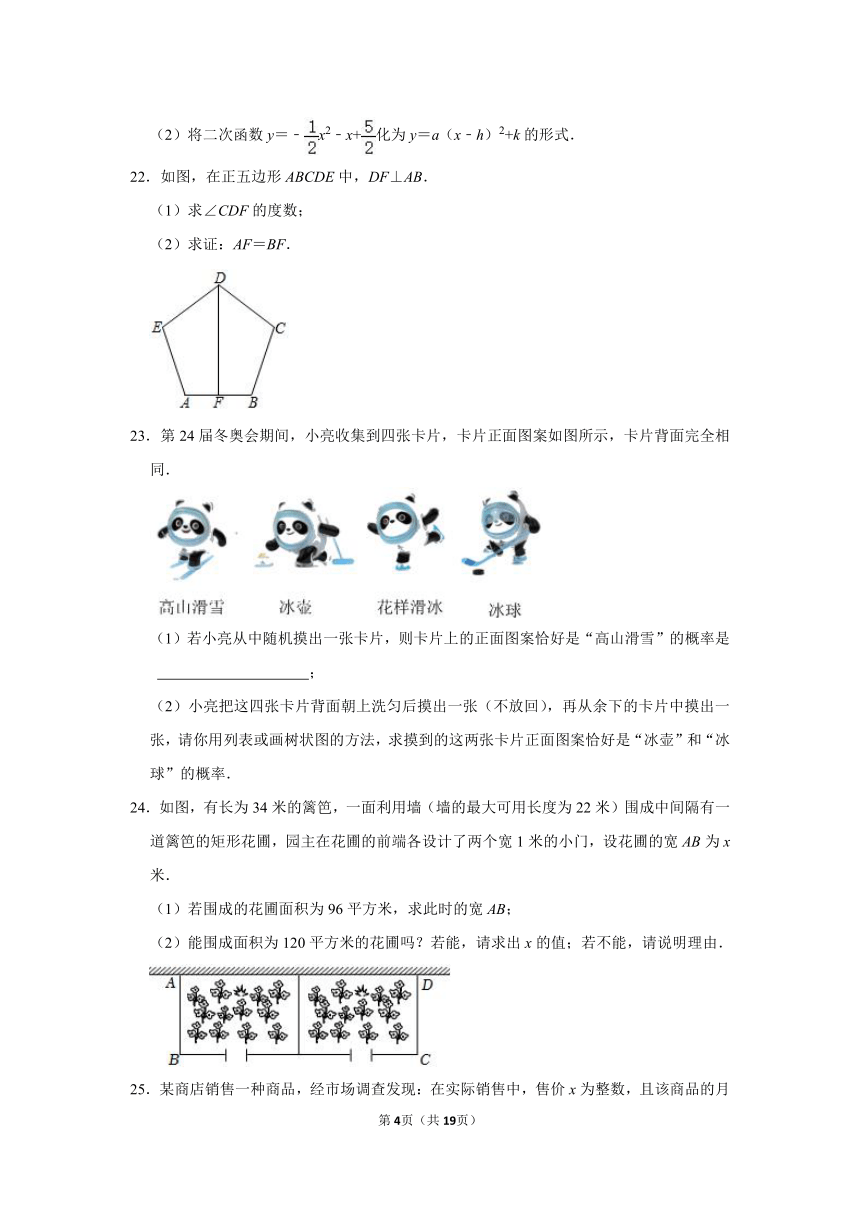
22.如图,在正五边形ABCDE中,DF⊥AB.
(1)求∠CDF的度数;
(2)求证:AF=BF.
23.第24届冬奥会期间,小亮收集到四张卡片,卡片正面图案如图所示,卡片背面完全相同.
(1)若小亮从中随机摸出一张卡片,则卡片上的正面图案恰好是“高山滑雪”的概率是 ;
(2)小亮把这四张卡片背面朝上洗匀后摸出一张(不放回),再从余下的卡片中摸出一张,请你用列表或画树状图的方法,求摸到的这两张卡片正面图案恰好是“冰壶”和“冰球”的概率.
24.如图,有长为34米的篱笆,一面利用墙(墙的最大可用长度为22米)围成中间隔有一道篱笆的矩形花圃,园主在花圃的前端各设计了两个宽1米的小门,设花圃的宽AB为x米.
(1)若围成的花圃面积为96平方米,求此时的宽AB;
(2)能围成面积为120平方米的花圃吗?若能,请求出x的值;若不能,请说明理由.
25.某商店销售一种商品,经市场调查发现:在实际销售中,售价x为整数,且该商品的月销售量y(件)是售价x(元/件)的一次函数,其售价x(元/件)、月销售量y(件)、月销售利润w(元)的部分对应值如表:
售价x(元/件) 40 45
月销售量y(件) 300 250
月销售利润w(元) 3000 3750
注:月销售利润=月销售量×(售价﹣进价)
(1)求y关于x的函数表达式;
(2)当该商品的售价是多少元时,月销售利润最大?并求出最大利润;
(3)现公司决定每销售1件商品就捐赠m元利润(m≤6)给“精准扶贫”对象,要求:在售价不超过52元时,每月扣除捐赠后的月销售利润随售价x的增大而增大,求m的取值范围.
26.如图,点A、B在⊙O上,请你仅用无刻度的直尺,根据下列条件分别画出图①和图②中∠A的一个余角(保留画图痕迹,不写作法)
(1)在图①中,点C在⊙O上;
(2)在图②中,点C在⊙O内.
参考答案
一.选择题(共6小题)
1.若(m+4)x|m|﹣2﹣x﹣5=0是关于x的一元二次方程,则m的值为( )
A.4 B.﹣4 C.±4 D.±2
【答案】A
【解答】解:∵(m+4)x|m|﹣2﹣x﹣5=0是关于x的一元二次方程,
∴,
∴,
解得m=4.
故选:A.
2.已知⊙O的直径为5,若PO=3,则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法判断
【答案】C
【解答】解:圆的半径r=×5=2.5,点P到O的距离d=PO=3,
∴d>r,
∴点P在圆外,
故选:C.
3.某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行综合考核(考核的满分均为100分),三个方面的重要性之比依次为3:5:2.小王经过考核后所得的各项分数依次为90、88、85分,那么小王的最后综合得分是( )
A.87 B.87.5 C.87.6 D.88
【答案】D
【解答】解:由题意可得,
小王的最后综合得分是:=88(分),
故选:D.
4.已知A(x1,y1)、B(x2,y2)为二次函数y=﹣(x﹣1)2+k图象上两点,且x1<x2<1,则下列说法正确的是( )
A.y1+y2>0 B.y1+y2<0 C.y1﹣y2>0 D.y1﹣y2<0
【答案】D
【解答】解:∵二次函数y=﹣(x﹣1)2+k图象的对称轴为直线x=1,
开口向下,而x1<x2<1,
∴y1<y2,
即y1﹣y2<0.
故选:D.
5.二次函数y=(x﹣1)2﹣2,若y随x的增大而增大,则x的取值范围是( )
A.x>1 B.x<1 C.x>﹣1 D.x<﹣1
【答案】A
【解答】解:∵二次函数y=(x﹣1)2+2,
∴当x>1时,y随x的增大而增大,当x<1时,y随x的增大而减小,
故选:A.
6.如图,AB是⊙O的直径,CD是⊙O的切线,D为切点,AC⊥CD,垂足为C,连接BD.若AB=8,且∠B=30°,则CD的长为( )
A.2 B.2 C.4 D.4
【答案】B
【解答】解:如图,连接OD,AD,
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠ODC=90°,
∵AB是⊙O的直径,AB=8,
∴OA=OB=OD=4,
∴∠ODB=∠ABC=30°,
∴∠BAD=∠AOD=60°,
∴△OAD是等边三角形,
∴∠DO=60°,
∴∠ADC=30°,
∴AC=AD=OA=2,
∴CD=AC=2,
故选:B.
二.填空题(共12小题)
7.已知某校学生“科技创新社团”成员的年龄与人数情况如下表所示:那么“科技创新社团”成员年龄的中位数是 14 岁.
年龄(岁) 11 12 13 14 15
人数 5 5 16 15 12
【答案】14.
【解答】解:该校学生“科技创新社团”的人数为5+5+16+15+12=53(人),
将这53人的年龄从小到大排列后,处在中间位置的一个数为14岁,因此中位数是14岁,
故答案为:14.
8.将抛物线y=2(x+4)2向右平移3个单位,得到新抛物线的表达式是 y=2(x+1)2 .
【答案】y=2(x+1)2.
【解答】解:y=2(x+4)2的顶点坐标为(﹣4,0),
∵向右平移3个单位,
∴平移后的抛物线的顶点坐标为(﹣1,0),
∴所得到的新抛物线的表达式是y=2(x+1)2.
故答案为:y=2(x+1)2.
9.在一个不透明的袋中装有7个红球和3个白球,这些球除颜色外无其他差别,随机从袋中摸出一个球,这个球是白球的概率是 .
【答案】见试题解答内容
【解答】解:P(这个球是白球)==.
故答案为:.
10.某店8月份利润为16万元,要使10月份利润达到25万元,设月平均增长率为x,根据题意可列方程 16(1+x)2=25 .
【答案】16(1+x)2=25.
【解答】解:平均每月增长的百分率是x,依题意得16(1+x)2=25.
故答案为:16(1+x)2=25.
11.甲、乙两名同学5次数学考试的平均成绩都是102分,方差分别为S甲2=38,S乙2=10,则 乙 同学的数学成绩更稳定.
【答案】乙.
【解答】解:由题干可知,甲的方差比乙的方差大,根据方差越小越稳定可判断,乙同学成绩更加稳定.
故答案:乙.
12.弧长为8π半径为12的扇形,它的圆心角的度数是 120° .
【答案】见试题解答内容
【解答】解:∵扇形的弧长为8π,半径为12,
∴设它的圆心角的度数是n°,则l==8π,
解得:n=120°.
故答案为:120°.
13.抛物线y=x2+x不经过第 四 象限.
【答案】四.
【解答】解:令x=0,y=x2+x=0,则抛物线过原点(0,0),
抛物线y=x2+x化为顶点式y=,
故可知其顶点为(﹣,)位于第三象限,且开口向上,则其不经过第四象限,
故答案为:四.
14.如图,AB是⊙O的弦,连接BO,作AC⊥BO交BO的延长线于点C,已知OC=,BO=2,点D是的中点,连接CD,则CD的长为 .
【答案】.
【解答】解:如图,连接OA、OD、AD,
∵OA=0B=2,OC=,AC⊥BO,
∴∠OAC=30°,∠AOC=60°,
∴∠OAB=∠OBA=30°,
在Rt△ABC中,
AC=,
∵点D是,
∴∠AOD=∠BOD=60°,
∴△AOD为等边三角形,
∴AD=AO=2,
在Rt△ACD中,
CD==.
故答案为:.
15.若m是方程2x2﹣3x﹣1=0的一个根,则6m2﹣9m+2023的值为 2026 .
【答案】2026.
【解答】解:∵m是方程2x2﹣3x﹣1=0的一个根,
∴2m2﹣3m﹣1=0,2m2﹣3m=1,
则6m2﹣9m+2023=3(2m2﹣3m)+2023=3+2023=2026,
故答案为:2026.
16.测量7名学生的体温(单位:℃)如下:36.5,36.3,36.8,36.3,36.5,36.7,36.5,这组数据的众数是 36.5 ℃.
【答案】36.5.
【解答】解:这七个数据中出现次数最多的是36.5,共出现3次,因此众数是36.5,
故答案为:36.5.
17.抛物线y=ax2+bx+c(a≠0)的图象如图所示,抛物线经过点(﹣1,0),则下列结论:①abc<0;②2a﹣b>0;③3a+c>0;④a+b>am2+bm(m为一切实数);⑤b2>4ac;正确的是 ①⑤ (填写序号).
【答案】①⑤.
【解答】解:①∵图象开口向下,与y轴交于正半轴,对称轴在y轴右侧,
∴a<0,c>0,﹣>0,
∴b>0,
∴abc<0,故正确;
②∵a<0,b>0,
∴2a﹣b<0,故错误;
③∵对称轴x=﹣=1,
∴b=﹣2a,
∵当x=﹣1时,y=0,即a﹣b+c=0,
∴3a+c=0.故错误;
④x=1函数有最大值,故a+b+c≥am2+bm+c,则a+b≥am2+bm(m为一切实数),
故错误.
⑤抛物线与x轴有2个交点,则b2﹣4ac>0,即b2>4ac.
故正确;
综上所述,正确的结论是①⑤.
故答案为:①⑤.
18.小球在如图所示的地板上自由地滚动,并最终随机地停留在某块方砖上(每块方砖除颜色外完全相同),则小球停留在黑色区域的概率是 .
【答案】.
【解答】解:由图可知,黑色方砖5块,共有9块方砖,
∴黑色方砖在整个地板中所占的比值=,
∴它停在黑色区域的概率是.
故答案为:.
三.解答题(共8小题)
19.用适当的方法解方程:
(1)x2+4x﹣2=0;
(2)2x2﹣3x+1=0.
【答案】(1)x1=﹣2+,x2=﹣2﹣;
(2)x1=,x2=1.
【解答】解:(1)x2+4x﹣2=0,
移项,得x2+4x=2,
配方,得x2+4x+4=2+4,
(x+2)2=6,
开方,得x+2=,
解得:x1=﹣2+,x2=﹣2﹣;
(2)2x2﹣3x+1=0,
(2x﹣1)(x﹣1)=0,
2x﹣1=0或x﹣1=0,
解得:x1=,x2=1.
20.为了缅怀先烈,向中国人民志愿军致敬,近两年涌现了很多抗美援朝的电影作品,《长津湖》和《狙击手》正是其中优秀的代表.为了解学生对这两部作品的评价,某调查小组从该学校观看过这两部电影的学生中各随机抽取了20名学生对这两部作品分别进行评分,并通过整理和分析,给出了部分信息.
抽取的学生对两部作品分别评分的平均数,众数和中位数:
平均数 众数 中位数
《长津湖》 8.2 9 b
《狙击手》 ﹣﹣﹣﹣ c 8
根据以上信息,解答下列问题:
(1)上述图表中的a= 15 ,b= 8.5 ,c= 8 .
(2)求《狙击手》评分的平均数;
(3)若该校有1000名学生观看过这两部影片,若他们都对这两部作品进行评分,你认为这两部作品一共可得到多少个满分?
【答案】(1)15,8.5,8;
(2)7.8;
(3)350个.
【解答】解:(1)《狙击手》得分为“10分”所占的百分比为:1﹣10%﹣20%﹣20%﹣=15%,即a=15,
《长津湖》得分从小到大排列处在中间位置的两个数的平均数为=8.5,因此中位数是8.5,即b=8.5,
《狙击手》得分出现次数最多的是8分,共出现×20=7(次),因此众数是8,即c=8.
故答案为:15,8.5,8;
(2)《狙击手》评分的平均数为10×15%+9×10%+8×+7×20%+6×20%=7.8;
(3)1000×(+15%)=350(个).
答:这两部作品一共大约可得到350个满分.
21.(1)解方程:3(x﹣2)2=2(x﹣2);
(2)将二次函数y=﹣x2﹣x+化为y=a(x﹣h)2+k的形式.
【答案】(1)x1=2,x2=;
(2)y=﹣(x+1)2+3.
【解答】解:(1)3(x﹣2)2=2(x﹣2),
3(x﹣2)2﹣2(x﹣2)=0,
(x﹣2)(3x﹣6﹣2)=0,
则x﹣2=0或3x﹣8=0,
解得:x1=2,x2=;
(2)y=﹣x2﹣x+
=﹣(x2+2x+1﹣1)+
=﹣(x+1)2+3.
22.如图,在正五边形ABCDE中,DF⊥AB.
(1)求∠CDF的度数;
(2)求证:AF=BF.
【答案】(1)54°;
(2)证明过程见解答.
【解答】(1)解:在正五边形中,∠ABC=∠C=540°÷5=108°,
∵DF⊥AB,
∴∠DFB=90°,
在四边形BCDF中,
∵∠ABC+∠C+∠DFB+∠CDF=360°,
∴∠CDF=360°﹣∠ABC﹣∠C﹣∠DFB=360°﹣108°﹣108°﹣90°=54°;
(2)证明:如图,连接DB、AD,
∵五边形ABCDE是正五边形,
∴∠E=∠C,DE=AE=DC=BC,
在△AED和△BCD中,
,
∴△AED≌△BCD(SAS),
∴AD=BD,
∵DF⊥AB,
∴∠DFA=∠DFB=90°,
Rt△DAF和Rt△DFB,
,
∴Rt△DAF≌Rt△DFB(HL),
∴AF=BF.
23.第24届冬奥会期间,小亮收集到四张卡片,卡片正面图案如图所示,卡片背面完全相同.
(1)若小亮从中随机摸出一张卡片,则卡片上的正面图案恰好是“高山滑雪”的概率是 ;
(2)小亮把这四张卡片背面朝上洗匀后摸出一张(不放回),再从余下的卡片中摸出一张,请你用列表或画树状图的方法,求摸到的这两张卡片正面图案恰好是“冰壶”和“冰球”的概率.
【答案】(1);
(2).
【解答】解:(1)若小亮从中随机摸出一张卡片,则卡片上的正面图案恰好是“高山滑雪”的概率是,
故答案为:;
(2)把这四张卡片分别记为A,B,C,D,画树状图如下,
共有12种等可能的结果,其中两张卡片正面图案恰好是“冰壶”和“冰球”的结果有2种,
∴摸到的这两张卡片正面图案恰好是“冰壶”和“冰球”的概率为.
24.如图,有长为34米的篱笆,一面利用墙(墙的最大可用长度为22米)围成中间隔有一道篱笆的矩形花圃,园主在花圃的前端各设计了两个宽1米的小门,设花圃的宽AB为x米.
(1)若围成的花圃面积为96平方米,求此时的宽AB;
(2)能围成面积为120平方米的花圃吗?若能,请求出x的值;若不能,请说明理由.
【答案】(1)此时宽AB为8米;
(2)不能围成面积为120平方米的花圃.理由见解答.
【解答】解:(1)∵花圃的宽AB为x米,
∴花圃的长AD为(34+2﹣3x)米.
依题意得:x(34+2﹣3x)=96,
解得:x1=4,x2=8.
当x=4时,34+2﹣3x=24>22,不合题意,舍去;
当x=8时,34+2﹣3x=12<22,符合题意.
答:此时宽AB为8米;
(2)不能围成面积为120平方米的花圃,理由如下:
依题意得:x(34+2﹣3x)=120,
整理得:x2﹣12x+40=0,
∵Δ=(﹣12)2﹣4×1×40=﹣16<0,
∴该方程无实数根,
即不能围成面积为120平方米的花圃.
25.某商店销售一种商品,经市场调查发现:在实际销售中,售价x为整数,且该商品的月销售量y(件)是售价x(元/件)的一次函数,其售价x(元/件)、月销售量y(件)、月销售利润w(元)的部分对应值如表:
售价x(元/件) 40 45
月销售量y(件) 300 250
月销售利润w(元) 3000 3750
注:月销售利润=月销售量×(售价﹣进价)
(1)求y关于x的函数表达式;
(2)当该商品的售价是多少元时,月销售利润最大?并求出最大利润;
(3)现公司决定每销售1件商品就捐赠m元利润(m≤6)给“精准扶贫”对象,要求:在售价不超过52元时,每月扣除捐赠后的月销售利润随售价x的增大而增大,求m的取值范围.
【答案】(1)y与x的函数表达式为y=﹣10x+700;(2)当该商品的售价是50元时,月销售利润最大,最大利润为4000元;(3)m的取值范围为3<m≤6.
【解答】解:(1)设一次函数解析式为y=kx+b,
根据题意,得
,
解得:,
所以y与x的函数表达式为y=﹣10x+700;
(2)由表中数据知,每件商品进价为=30(元),
设该商品的月销售利润为w元,
则w=(x﹣30)y=(x﹣30)(﹣10x+700)=﹣10x2+1000x﹣21000=﹣10(x﹣50)2+4000,
∵﹣10<0,
∴当x=50时,w最大,最大值为4000,
∴当该商品的售价是50元时,月销售利润最大,最大利润为4000元;
(3)根据题意得:w=(x﹣30﹣m)(﹣10x+700)=﹣10x2+(1000+10m)x﹣21000﹣700m,
对称轴为直线x=﹣=50+,
∵﹣10<0,
∴当x≤50+时,w随x的增大而增大,
∵x≤52时,每月扣除捐赠后的月销售利润随售价x的增大而增大,
∴50+>51.5,
解得:m>3,
∵3<m≤6,
∴m的取值范围为3<m≤6.
26.如图,点A、B在⊙O上,请你仅用无刻度的直尺,根据下列条件分别画出图①和图②中∠A的一个余角(保留画图痕迹,不写作法)
(1)在图①中,点C在⊙O上;
(2)在图②中,点C在⊙O内.
【答案】见试题解答内容
【解答】解:(1)如图①,∠DBC就是所求的角;
(2)如图②,∠FBE就是所求的角.
第1页(共1页)
一.选择题(共6小题)
1.若(m+4)x|m|﹣2﹣x﹣5=0是关于x的一元二次方程,则m的值为( )
A.4 B.﹣4 C.±4 D.±2
2.已知⊙O的直径为5,若PO=3,则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法判断
3.某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行综合考核(考核的满分均为100分),三个方面的重要性之比依次为3:5:2.小王经过考核后所得的各项分数依次为90、88、85分,那么小王的最后综合得分是( )
A.87 B.87.5 C.87.6 D.88
4.已知A(x1,y1)、B(x2,y2)为二次函数y=﹣(x﹣1)2+k图象上两点,且x1<x2<1,则下列说法正确的是( )
A.y1+y2>0 B.y1+y2<0 C.y1﹣y2>0 D.y1﹣y2<0
5.二次函数y=(x﹣1)2﹣2,若y随x的增大而增大,则x的取值范围是( )
A.x>1 B.x<1 C.x>﹣1 D.x<﹣1
6.如图,AB是⊙O的直径,CD是⊙O的切线,D为切点,AC⊥CD,垂足为C,连接BD.若AB=8,且∠B=30°,则CD的长为( )
A.2 B.2 C.4 D.4
二.填空题(共12小题)
7.已知某校学生“科技创新社团”成员的年龄与人数情况如下表所示:那么“科技创新社团”成员年龄的中位数是 岁.
年龄(岁) 11 12 13 14 15
人数 5 5 16 15 12
8.将抛物线y=2(x+4)2向右平移3个单位,得到新抛物线的表达式是 .
9.在一个不透明的袋中装有7个红球和3个白球,这些球除颜色外无其他差别,随机从袋中摸出一个球,这个球是白球的概率是 .
10.某店8月份利润为16万元,要使10月份利润达到25万元,设月平均增长率为x,根据题意可列方程 .
11.甲、乙两名同学5次数学考试的平均成绩都是102分,方差分别为S甲2=38,S乙2=10,则 同学的数学成绩更稳定.
12.弧长为8π半径为12的扇形,它的圆心角的度数是 .
13.抛物线y=x2+x不经过第 象限.
14.如图,AB是⊙O的弦,连接BO,作AC⊥BO交BO的延长线于点C,已知OC=,BO=2,点D是的中点,连接CD,则CD的长为 .
15.若m是方程2x2﹣3x﹣1=0的一个根,则6m2﹣9m+2023的值为 .
16.测量7名学生的体温(单位:℃)如下:36.5,36.3,36.8,36.3,36.5,36.7,36.5,这组数据的众数是 ℃.
17.抛物线y=ax2+bx+c(a≠0)的图象如图所示,抛物线经过点(﹣1,0),则下列结论:①abc<0;②2a﹣b>0;③3a+c>0;④a+b>am2+bm(m为一切实数);⑤b2>4ac;正确的是 (填写序号).
18.小球在如图所示的地板上自由地滚动,并最终随机地停留在某块方砖上(每块方砖除颜色外完全相同),则小球停留在黑色区域的概率是 .
三.解答题(共8小题)
19.用适当的方法解方程:
(1)x2+4x﹣2=0;
(2)2x2﹣3x+1=0.
20.为了缅怀先烈,向中国人民志愿军致敬,近两年涌现了很多抗美援朝的电影作品,《长津湖》和《狙击手》正是其中优秀的代表.为了解学生对这两部作品的评价,某调查小组从该学校观看过这两部电影的学生中各随机抽取了20名学生对这两部作品分别进行评分,并通过整理和分析,给出了部分信息.
抽取的学生对两部作品分别评分的平均数,众数和中位数:
平均数 众数 中位数
《长津湖》 8.2 9 b
《狙击手》 ﹣﹣﹣﹣ c 8
根据以上信息,解答下列问题:
(1)上述图表中的a= ,b= ,c= .
(2)求《狙击手》评分的平均数;
(3)若该校有1000名学生观看过这两部影片,若他们都对这两部作品进行评分,你认为这两部作品一共可得到多少个满分?
21.(1)解方程:3(x﹣2)2=2(x﹣2);
(2)将二次函数y=﹣x2﹣x+化为y=a(x﹣h)2+k的形式.
22.如图,在正五边形ABCDE中,DF⊥AB.
(1)求∠CDF的度数;
(2)求证:AF=BF.
23.第24届冬奥会期间,小亮收集到四张卡片,卡片正面图案如图所示,卡片背面完全相同.
(1)若小亮从中随机摸出一张卡片,则卡片上的正面图案恰好是“高山滑雪”的概率是 ;
(2)小亮把这四张卡片背面朝上洗匀后摸出一张(不放回),再从余下的卡片中摸出一张,请你用列表或画树状图的方法,求摸到的这两张卡片正面图案恰好是“冰壶”和“冰球”的概率.
24.如图,有长为34米的篱笆,一面利用墙(墙的最大可用长度为22米)围成中间隔有一道篱笆的矩形花圃,园主在花圃的前端各设计了两个宽1米的小门,设花圃的宽AB为x米.
(1)若围成的花圃面积为96平方米,求此时的宽AB;
(2)能围成面积为120平方米的花圃吗?若能,请求出x的值;若不能,请说明理由.
25.某商店销售一种商品,经市场调查发现:在实际销售中,售价x为整数,且该商品的月销售量y(件)是售价x(元/件)的一次函数,其售价x(元/件)、月销售量y(件)、月销售利润w(元)的部分对应值如表:
售价x(元/件) 40 45
月销售量y(件) 300 250
月销售利润w(元) 3000 3750
注:月销售利润=月销售量×(售价﹣进价)
(1)求y关于x的函数表达式;
(2)当该商品的售价是多少元时,月销售利润最大?并求出最大利润;
(3)现公司决定每销售1件商品就捐赠m元利润(m≤6)给“精准扶贫”对象,要求:在售价不超过52元时,每月扣除捐赠后的月销售利润随售价x的增大而增大,求m的取值范围.
26.如图,点A、B在⊙O上,请你仅用无刻度的直尺,根据下列条件分别画出图①和图②中∠A的一个余角(保留画图痕迹,不写作法)
(1)在图①中,点C在⊙O上;
(2)在图②中,点C在⊙O内.
参考答案
一.选择题(共6小题)
1.若(m+4)x|m|﹣2﹣x﹣5=0是关于x的一元二次方程,则m的值为( )
A.4 B.﹣4 C.±4 D.±2
【答案】A
【解答】解:∵(m+4)x|m|﹣2﹣x﹣5=0是关于x的一元二次方程,
∴,
∴,
解得m=4.
故选:A.
2.已知⊙O的直径为5,若PO=3,则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法判断
【答案】C
【解答】解:圆的半径r=×5=2.5,点P到O的距离d=PO=3,
∴d>r,
∴点P在圆外,
故选:C.
3.某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行综合考核(考核的满分均为100分),三个方面的重要性之比依次为3:5:2.小王经过考核后所得的各项分数依次为90、88、85分,那么小王的最后综合得分是( )
A.87 B.87.5 C.87.6 D.88
【答案】D
【解答】解:由题意可得,
小王的最后综合得分是:=88(分),
故选:D.
4.已知A(x1,y1)、B(x2,y2)为二次函数y=﹣(x﹣1)2+k图象上两点,且x1<x2<1,则下列说法正确的是( )
A.y1+y2>0 B.y1+y2<0 C.y1﹣y2>0 D.y1﹣y2<0
【答案】D
【解答】解:∵二次函数y=﹣(x﹣1)2+k图象的对称轴为直线x=1,
开口向下,而x1<x2<1,
∴y1<y2,
即y1﹣y2<0.
故选:D.
5.二次函数y=(x﹣1)2﹣2,若y随x的增大而增大,则x的取值范围是( )
A.x>1 B.x<1 C.x>﹣1 D.x<﹣1
【答案】A
【解答】解:∵二次函数y=(x﹣1)2+2,
∴当x>1时,y随x的增大而增大,当x<1时,y随x的增大而减小,
故选:A.
6.如图,AB是⊙O的直径,CD是⊙O的切线,D为切点,AC⊥CD,垂足为C,连接BD.若AB=8,且∠B=30°,则CD的长为( )
A.2 B.2 C.4 D.4
【答案】B
【解答】解:如图,连接OD,AD,
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠ODC=90°,
∵AB是⊙O的直径,AB=8,
∴OA=OB=OD=4,
∴∠ODB=∠ABC=30°,
∴∠BAD=∠AOD=60°,
∴△OAD是等边三角形,
∴∠DO=60°,
∴∠ADC=30°,
∴AC=AD=OA=2,
∴CD=AC=2,
故选:B.
二.填空题(共12小题)
7.已知某校学生“科技创新社团”成员的年龄与人数情况如下表所示:那么“科技创新社团”成员年龄的中位数是 14 岁.
年龄(岁) 11 12 13 14 15
人数 5 5 16 15 12
【答案】14.
【解答】解:该校学生“科技创新社团”的人数为5+5+16+15+12=53(人),
将这53人的年龄从小到大排列后,处在中间位置的一个数为14岁,因此中位数是14岁,
故答案为:14.
8.将抛物线y=2(x+4)2向右平移3个单位,得到新抛物线的表达式是 y=2(x+1)2 .
【答案】y=2(x+1)2.
【解答】解:y=2(x+4)2的顶点坐标为(﹣4,0),
∵向右平移3个单位,
∴平移后的抛物线的顶点坐标为(﹣1,0),
∴所得到的新抛物线的表达式是y=2(x+1)2.
故答案为:y=2(x+1)2.
9.在一个不透明的袋中装有7个红球和3个白球,这些球除颜色外无其他差别,随机从袋中摸出一个球,这个球是白球的概率是 .
【答案】见试题解答内容
【解答】解:P(这个球是白球)==.
故答案为:.
10.某店8月份利润为16万元,要使10月份利润达到25万元,设月平均增长率为x,根据题意可列方程 16(1+x)2=25 .
【答案】16(1+x)2=25.
【解答】解:平均每月增长的百分率是x,依题意得16(1+x)2=25.
故答案为:16(1+x)2=25.
11.甲、乙两名同学5次数学考试的平均成绩都是102分,方差分别为S甲2=38,S乙2=10,则 乙 同学的数学成绩更稳定.
【答案】乙.
【解答】解:由题干可知,甲的方差比乙的方差大,根据方差越小越稳定可判断,乙同学成绩更加稳定.
故答案:乙.
12.弧长为8π半径为12的扇形,它的圆心角的度数是 120° .
【答案】见试题解答内容
【解答】解:∵扇形的弧长为8π,半径为12,
∴设它的圆心角的度数是n°,则l==8π,
解得:n=120°.
故答案为:120°.
13.抛物线y=x2+x不经过第 四 象限.
【答案】四.
【解答】解:令x=0,y=x2+x=0,则抛物线过原点(0,0),
抛物线y=x2+x化为顶点式y=,
故可知其顶点为(﹣,)位于第三象限,且开口向上,则其不经过第四象限,
故答案为:四.
14.如图,AB是⊙O的弦,连接BO,作AC⊥BO交BO的延长线于点C,已知OC=,BO=2,点D是的中点,连接CD,则CD的长为 .
【答案】.
【解答】解:如图,连接OA、OD、AD,
∵OA=0B=2,OC=,AC⊥BO,
∴∠OAC=30°,∠AOC=60°,
∴∠OAB=∠OBA=30°,
在Rt△ABC中,
AC=,
∵点D是,
∴∠AOD=∠BOD=60°,
∴△AOD为等边三角形,
∴AD=AO=2,
在Rt△ACD中,
CD==.
故答案为:.
15.若m是方程2x2﹣3x﹣1=0的一个根,则6m2﹣9m+2023的值为 2026 .
【答案】2026.
【解答】解:∵m是方程2x2﹣3x﹣1=0的一个根,
∴2m2﹣3m﹣1=0,2m2﹣3m=1,
则6m2﹣9m+2023=3(2m2﹣3m)+2023=3+2023=2026,
故答案为:2026.
16.测量7名学生的体温(单位:℃)如下:36.5,36.3,36.8,36.3,36.5,36.7,36.5,这组数据的众数是 36.5 ℃.
【答案】36.5.
【解答】解:这七个数据中出现次数最多的是36.5,共出现3次,因此众数是36.5,
故答案为:36.5.
17.抛物线y=ax2+bx+c(a≠0)的图象如图所示,抛物线经过点(﹣1,0),则下列结论:①abc<0;②2a﹣b>0;③3a+c>0;④a+b>am2+bm(m为一切实数);⑤b2>4ac;正确的是 ①⑤ (填写序号).
【答案】①⑤.
【解答】解:①∵图象开口向下,与y轴交于正半轴,对称轴在y轴右侧,
∴a<0,c>0,﹣>0,
∴b>0,
∴abc<0,故正确;
②∵a<0,b>0,
∴2a﹣b<0,故错误;
③∵对称轴x=﹣=1,
∴b=﹣2a,
∵当x=﹣1时,y=0,即a﹣b+c=0,
∴3a+c=0.故错误;
④x=1函数有最大值,故a+b+c≥am2+bm+c,则a+b≥am2+bm(m为一切实数),
故错误.
⑤抛物线与x轴有2个交点,则b2﹣4ac>0,即b2>4ac.
故正确;
综上所述,正确的结论是①⑤.
故答案为:①⑤.
18.小球在如图所示的地板上自由地滚动,并最终随机地停留在某块方砖上(每块方砖除颜色外完全相同),则小球停留在黑色区域的概率是 .
【答案】.
【解答】解:由图可知,黑色方砖5块,共有9块方砖,
∴黑色方砖在整个地板中所占的比值=,
∴它停在黑色区域的概率是.
故答案为:.
三.解答题(共8小题)
19.用适当的方法解方程:
(1)x2+4x﹣2=0;
(2)2x2﹣3x+1=0.
【答案】(1)x1=﹣2+,x2=﹣2﹣;
(2)x1=,x2=1.
【解答】解:(1)x2+4x﹣2=0,
移项,得x2+4x=2,
配方,得x2+4x+4=2+4,
(x+2)2=6,
开方,得x+2=,
解得:x1=﹣2+,x2=﹣2﹣;
(2)2x2﹣3x+1=0,
(2x﹣1)(x﹣1)=0,
2x﹣1=0或x﹣1=0,
解得:x1=,x2=1.
20.为了缅怀先烈,向中国人民志愿军致敬,近两年涌现了很多抗美援朝的电影作品,《长津湖》和《狙击手》正是其中优秀的代表.为了解学生对这两部作品的评价,某调查小组从该学校观看过这两部电影的学生中各随机抽取了20名学生对这两部作品分别进行评分,并通过整理和分析,给出了部分信息.
抽取的学生对两部作品分别评分的平均数,众数和中位数:
平均数 众数 中位数
《长津湖》 8.2 9 b
《狙击手》 ﹣﹣﹣﹣ c 8
根据以上信息,解答下列问题:
(1)上述图表中的a= 15 ,b= 8.5 ,c= 8 .
(2)求《狙击手》评分的平均数;
(3)若该校有1000名学生观看过这两部影片,若他们都对这两部作品进行评分,你认为这两部作品一共可得到多少个满分?
【答案】(1)15,8.5,8;
(2)7.8;
(3)350个.
【解答】解:(1)《狙击手》得分为“10分”所占的百分比为:1﹣10%﹣20%﹣20%﹣=15%,即a=15,
《长津湖》得分从小到大排列处在中间位置的两个数的平均数为=8.5,因此中位数是8.5,即b=8.5,
《狙击手》得分出现次数最多的是8分,共出现×20=7(次),因此众数是8,即c=8.
故答案为:15,8.5,8;
(2)《狙击手》评分的平均数为10×15%+9×10%+8×+7×20%+6×20%=7.8;
(3)1000×(+15%)=350(个).
答:这两部作品一共大约可得到350个满分.
21.(1)解方程:3(x﹣2)2=2(x﹣2);
(2)将二次函数y=﹣x2﹣x+化为y=a(x﹣h)2+k的形式.
【答案】(1)x1=2,x2=;
(2)y=﹣(x+1)2+3.
【解答】解:(1)3(x﹣2)2=2(x﹣2),
3(x﹣2)2﹣2(x﹣2)=0,
(x﹣2)(3x﹣6﹣2)=0,
则x﹣2=0或3x﹣8=0,
解得:x1=2,x2=;
(2)y=﹣x2﹣x+
=﹣(x2+2x+1﹣1)+
=﹣(x+1)2+3.
22.如图,在正五边形ABCDE中,DF⊥AB.
(1)求∠CDF的度数;
(2)求证:AF=BF.
【答案】(1)54°;
(2)证明过程见解答.
【解答】(1)解:在正五边形中,∠ABC=∠C=540°÷5=108°,
∵DF⊥AB,
∴∠DFB=90°,
在四边形BCDF中,
∵∠ABC+∠C+∠DFB+∠CDF=360°,
∴∠CDF=360°﹣∠ABC﹣∠C﹣∠DFB=360°﹣108°﹣108°﹣90°=54°;
(2)证明:如图,连接DB、AD,
∵五边形ABCDE是正五边形,
∴∠E=∠C,DE=AE=DC=BC,
在△AED和△BCD中,
,
∴△AED≌△BCD(SAS),
∴AD=BD,
∵DF⊥AB,
∴∠DFA=∠DFB=90°,
Rt△DAF和Rt△DFB,
,
∴Rt△DAF≌Rt△DFB(HL),
∴AF=BF.
23.第24届冬奥会期间,小亮收集到四张卡片,卡片正面图案如图所示,卡片背面完全相同.
(1)若小亮从中随机摸出一张卡片,则卡片上的正面图案恰好是“高山滑雪”的概率是 ;
(2)小亮把这四张卡片背面朝上洗匀后摸出一张(不放回),再从余下的卡片中摸出一张,请你用列表或画树状图的方法,求摸到的这两张卡片正面图案恰好是“冰壶”和“冰球”的概率.
【答案】(1);
(2).
【解答】解:(1)若小亮从中随机摸出一张卡片,则卡片上的正面图案恰好是“高山滑雪”的概率是,
故答案为:;
(2)把这四张卡片分别记为A,B,C,D,画树状图如下,
共有12种等可能的结果,其中两张卡片正面图案恰好是“冰壶”和“冰球”的结果有2种,
∴摸到的这两张卡片正面图案恰好是“冰壶”和“冰球”的概率为.
24.如图,有长为34米的篱笆,一面利用墙(墙的最大可用长度为22米)围成中间隔有一道篱笆的矩形花圃,园主在花圃的前端各设计了两个宽1米的小门,设花圃的宽AB为x米.
(1)若围成的花圃面积为96平方米,求此时的宽AB;
(2)能围成面积为120平方米的花圃吗?若能,请求出x的值;若不能,请说明理由.
【答案】(1)此时宽AB为8米;
(2)不能围成面积为120平方米的花圃.理由见解答.
【解答】解:(1)∵花圃的宽AB为x米,
∴花圃的长AD为(34+2﹣3x)米.
依题意得:x(34+2﹣3x)=96,
解得:x1=4,x2=8.
当x=4时,34+2﹣3x=24>22,不合题意,舍去;
当x=8时,34+2﹣3x=12<22,符合题意.
答:此时宽AB为8米;
(2)不能围成面积为120平方米的花圃,理由如下:
依题意得:x(34+2﹣3x)=120,
整理得:x2﹣12x+40=0,
∵Δ=(﹣12)2﹣4×1×40=﹣16<0,
∴该方程无实数根,
即不能围成面积为120平方米的花圃.
25.某商店销售一种商品,经市场调查发现:在实际销售中,售价x为整数,且该商品的月销售量y(件)是售价x(元/件)的一次函数,其售价x(元/件)、月销售量y(件)、月销售利润w(元)的部分对应值如表:
售价x(元/件) 40 45
月销售量y(件) 300 250
月销售利润w(元) 3000 3750
注:月销售利润=月销售量×(售价﹣进价)
(1)求y关于x的函数表达式;
(2)当该商品的售价是多少元时,月销售利润最大?并求出最大利润;
(3)现公司决定每销售1件商品就捐赠m元利润(m≤6)给“精准扶贫”对象,要求:在售价不超过52元时,每月扣除捐赠后的月销售利润随售价x的增大而增大,求m的取值范围.
【答案】(1)y与x的函数表达式为y=﹣10x+700;(2)当该商品的售价是50元时,月销售利润最大,最大利润为4000元;(3)m的取值范围为3<m≤6.
【解答】解:(1)设一次函数解析式为y=kx+b,
根据题意,得
,
解得:,
所以y与x的函数表达式为y=﹣10x+700;
(2)由表中数据知,每件商品进价为=30(元),
设该商品的月销售利润为w元,
则w=(x﹣30)y=(x﹣30)(﹣10x+700)=﹣10x2+1000x﹣21000=﹣10(x﹣50)2+4000,
∵﹣10<0,
∴当x=50时,w最大,最大值为4000,
∴当该商品的售价是50元时,月销售利润最大,最大利润为4000元;
(3)根据题意得:w=(x﹣30﹣m)(﹣10x+700)=﹣10x2+(1000+10m)x﹣21000﹣700m,
对称轴为直线x=﹣=50+,
∵﹣10<0,
∴当x≤50+时,w随x的增大而增大,
∵x≤52时,每月扣除捐赠后的月销售利润随售价x的增大而增大,
∴50+>51.5,
解得:m>3,
∵3<m≤6,
∴m的取值范围为3<m≤6.
26.如图,点A、B在⊙O上,请你仅用无刻度的直尺,根据下列条件分别画出图①和图②中∠A的一个余角(保留画图痕迹,不写作法)
(1)在图①中,点C在⊙O上;
(2)在图②中,点C在⊙O内.
【答案】见试题解答内容
【解答】解:(1)如图①,∠DBC就是所求的角;
(2)如图②,∠FBE就是所求的角.
第1页(共1页)
同课章节目录
