2023-2024学年江苏省九年级数学期末突击模拟卷05(含解析)
文档属性
| 名称 | 2023-2024学年江苏省九年级数学期末突击模拟卷05(含解析) |  | |
| 格式 | Doc | ||
| 文件大小 | 940.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 16:33:58 | ||
图片预览


文档简介
2023-2024学年江苏省九年级数学期末突击模拟卷05
一.选择题(共8小题)
1.如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
A. B. C. D.
2.等腰三角形的腰长为2,底边长是方程x2﹣8x+15=0的根,则三角形的周长为( )
A.7 B.9 C.10 D.7或9
3.某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示,则该班学生一周读书时间的中位数和众数分别是( )
读书时间(小时) 7 8 9 10 11
学生人数 6 6 8 12 8
A.9.5,10 B.9.5,12 C.9,10 D.9,12
4.如图,△OAB∽△OCD,OA:OC=5:3,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A. B. C. D.
5.某快递公司今年一月份完成投递的快递总件数为10万件,二月份、三月份每月投递的件数逐月增加,第一季度总投递件数为33.1万件,问:二、三月份平均每月的增长率是多少?设平均每月增长的百分率为x,根据题意得方程( )
A.10(1+x)2=33.1
B.10(1+x)+10(1+x)2=33.1
C.10+10(1+x)2=33.1
D.10+10(1+x)+10(1+x)2=33.1
6.如图,将Rt△ABC平移到△A'B'C'的位置,其中∠C=90°使得点C'与△ABC的内心重合,已知AC=4,BC=3,则阴影部分的面积为( )
A. B. C. D.
7.下列说法正确的是( )
A.若甲、乙两组数据的平均数相同,S甲2=0.1,S乙2=0.04,则乙组数据较稳定
B.如果明天降水的概率是50%,那么明天有半天都在降雨
C.了解全国中学生的节水意识应选用普查方式
D.早上的太阳从西方升起是必然事件
8.如图,菱形ABCD中,∠B=60°,AB=4,以AD为直径的⊙O交CD于点E,则劣弧的长为( )
A. B. C. D.
二.填空题(共8小题)
9.若3x=4y且xy≠0,则的值等于 .
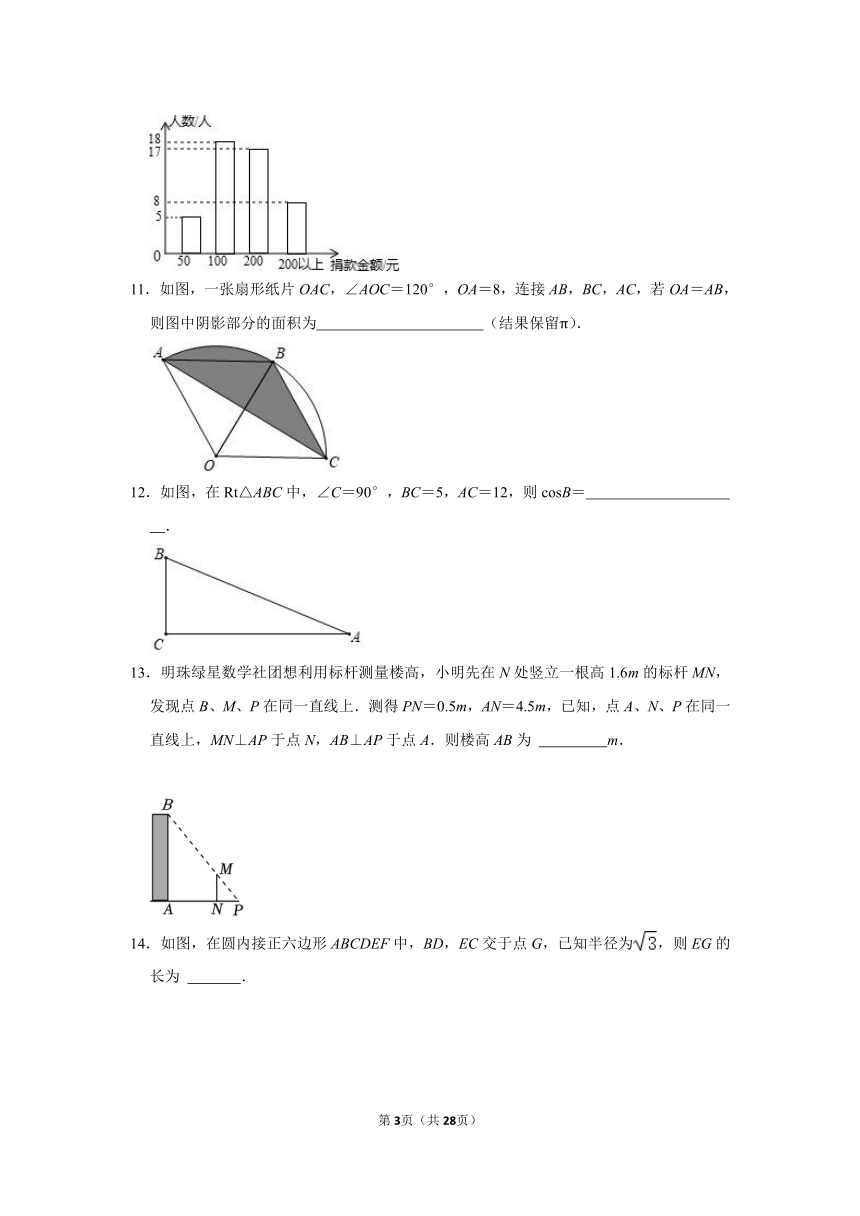
10.在某公益活动中,某社区对本社区的捐款情况进行了统计,如图是该社区捐款情况的条形统计图,则本次捐款金额的中位数是 元.
11.如图,一张扇形纸片OAC,∠AOC=120°,OA=8,连接AB,BC,AC,若OA=AB,则图中阴影部分的面积为 (结果保留π).
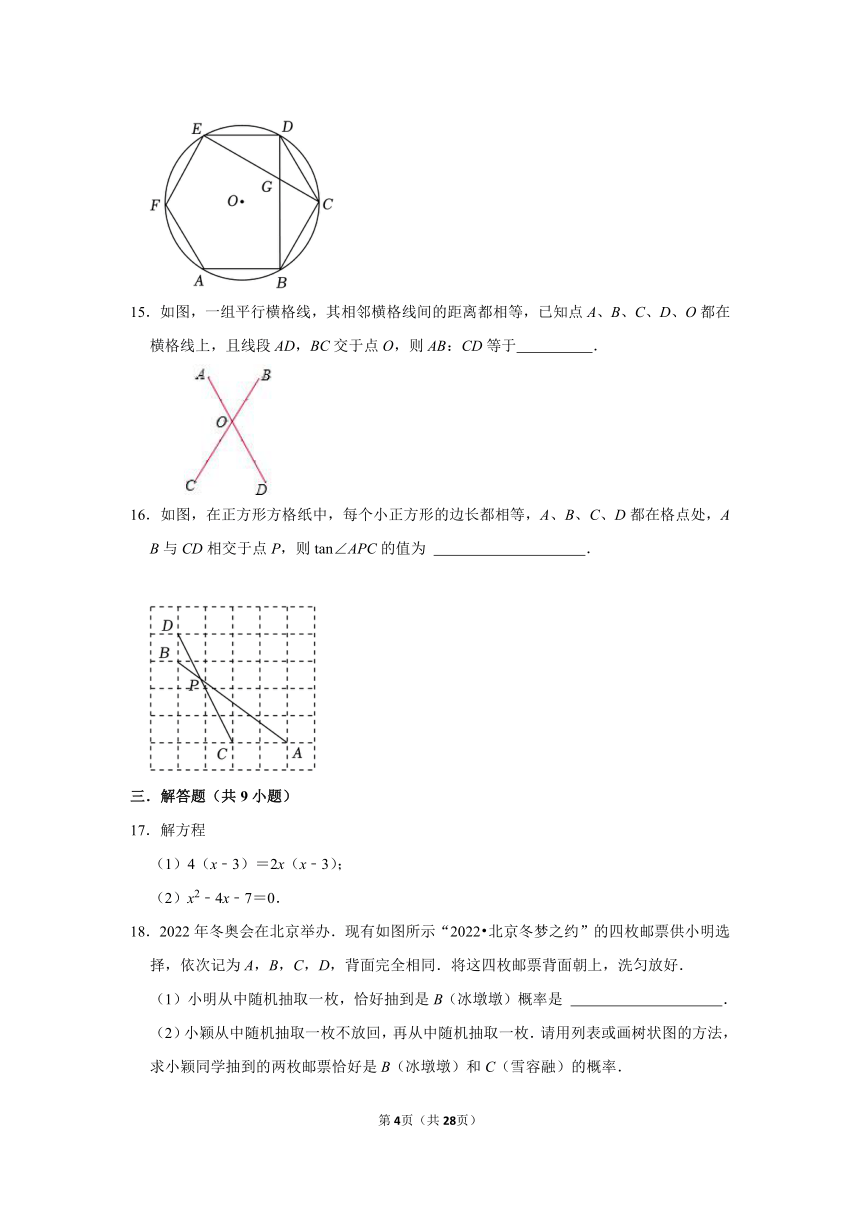
12.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,则cosB= .
13.明珠绿星数学社团想利用标杆测量楼高,小明先在N处竖立一根高1.6m的标杆MN,发现点B、M、P在同一直线上.测得PN=0.5m,AN=4.5m,已知,点A、N、P在同一直线上,MN⊥AP于点N,AB⊥AP于点A.则楼高AB为 m.
14.如图,在圆内接正六边形ABCDEF中,BD,EC交于点G,已知半径为,则EG的长为 .
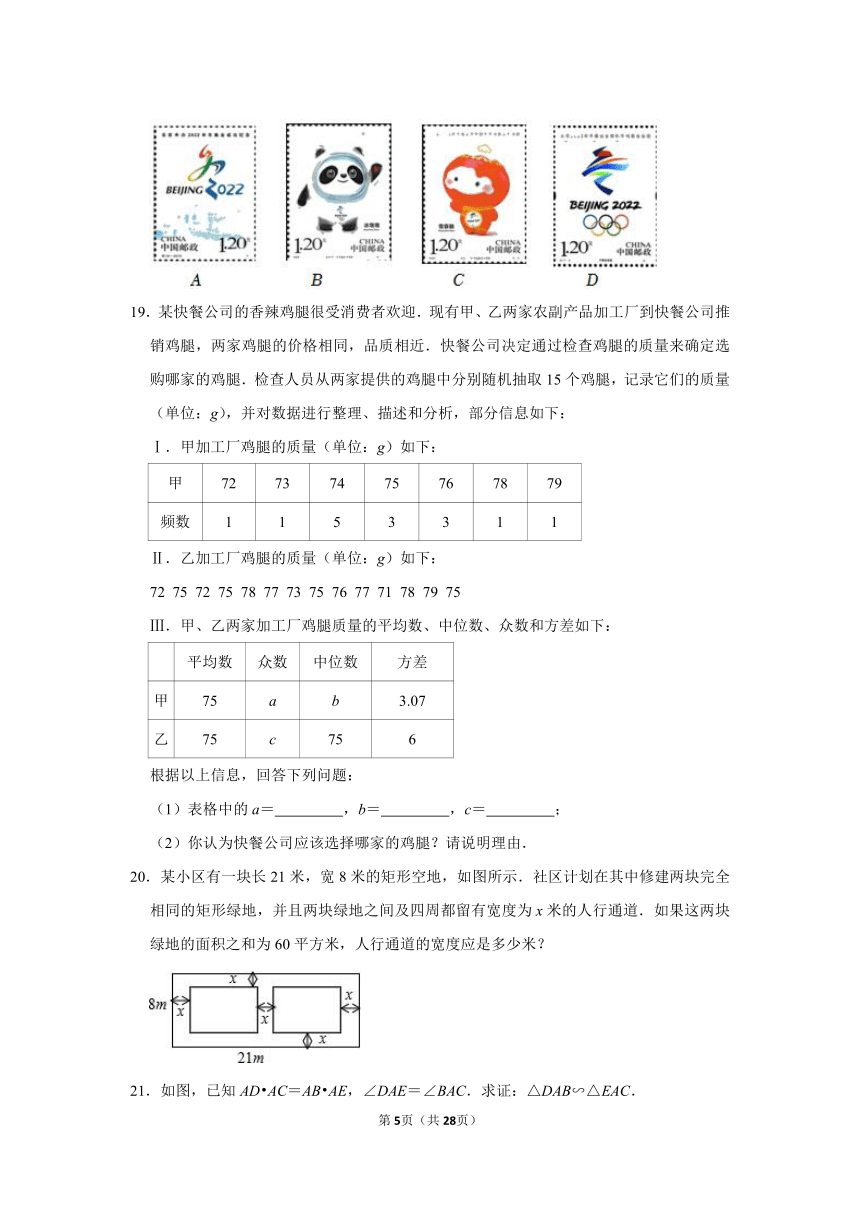
15.如图,一组平行横格线,其相邻横格线间的距离都相等,已知点A、B、C、D、O都在横格线上,且线段AD,BC交于点O,则AB:CD等于 .
16.如图,在正方形方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB与CD相交于点P,则tan∠APC的值为 .
三.解答题(共9小题)
17.解方程
(1)4(x﹣3)=2x(x﹣3);
(2)x2﹣4x﹣7=0.
18.2022年冬奥会在北京举办.现有如图所示“2022 北京冬梦之约”的四枚邮票供小明选择,依次记为A,B,C,D,背面完全相同.将这四枚邮票背面朝上,洗匀放好.
(1)小明从中随机抽取一枚,恰好抽到是B(冰墩墩)概率是 .
(2)小颖从中随机抽取一枚不放回,再从中随机抽取一枚.请用列表或画树状图的方法,求小颖同学抽到的两枚邮票恰好是B(冰墩墩)和C(雪容融)的概率.
19.某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家提供的鸡腿中分别随机抽取15个鸡腿,记录它们的质量(单位:g),并对数据进行整理、描述和分析,部分信息如下:
Ⅰ.甲加工厂鸡腿的质量(单位:g)如下:
甲 72 73 74 75 76 78 79
频数 1 1 5 3 3 1 1
Ⅱ.乙加工厂鸡腿的质量(单位:g)如下:
72 75 72 75 78 77 73 75 76 77 71 78 79 75
Ⅲ.甲、乙两家加工厂鸡腿质量的平均数、中位数、众数和方差如下:
平均数 众数 中位数 方差
甲 75 a b 3.07
乙 75 c 75 6
根据以上信息,回答下列问题:
(1)表格中的a= ,b= ,c= ;
(2)你认为快餐公司应该选择哪家的鸡腿?请说明理由.
20.某小区有一块长21米,宽8米的矩形空地,如图所示.社区计划在其中修建两块完全相同的矩形绿地,并且两块绿地之间及四周都留有宽度为x米的人行通道.如果这两块绿地的面积之和为60平方米,人行通道的宽度应是多少米?
21.如图,已知AD AC=AB AE,∠DAE=∠BAC.求证:△DAB∽△EAC.
22.洛阳市栾川县老君山景区的老子铜像,是目前世界上最高的老子铜像.某数学活动小组用学到的锐角三角函数的知识去测量老子铜像的高度.如图,铜像底座CE的高度为21m,他们在测量点A(与C在同一水平线上)测得底座最高点E的仰角为20°,沿AC方向前进24m到达测量点B,测得老子铜像顶部D的仰角为60°.求老子铜像DE的高度(结果精确到0.1m.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,≈1.73)
23.如图,AB为⊙O的直径,CD为弦,CD⊥AB于点E,连接DO并延长交⊙O于点F,连接AF交CD于点G,CG=AG,连接AC.
(1)求证:AC∥DF;
(2)若AB=12,求AC和GD的长.
24.如图,在平行四边形ABCD中,AC、BD交于点O,又M、N分别是OA、OC的中点.
(1)求证:BM=DN;
(2)若AO=BD,试判断四边形MBND的形状,并证明你的结论.
25.如图,在等边△ABC中,D,E分别为AB,BC边上的点,DE=EF,∠DEF=60°.
(1)如图1,若点F在AC边上,求证:AD=CF;
(2)如图2,连CF.若∠FCB=30°,求证:AD=2BE;
(3)如图3,O是BC的中点,点H在△ABC内,∠BHC=120°,点M,N分别在CH,BH上,MO⊥NO,若∠CAM=α,直接写出∠BAN的度数(用含有α的式子表示).
参考答案
一.选择题(共8小题)
1.如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
A. B. C. D.
【答案】D
【解答】解:连接BC,
由题意可得:OB=OC=BC,
则△OBC是等边三角形,
故sin∠AOC=sin60°=.
故选:D.
2.等腰三角形的腰长为2,底边长是方程x2﹣8x+15=0的根,则三角形的周长为( )
A.7 B.9 C.10 D.7或9
【答案】A
【解答】解:∵x2﹣8x+15=0,
∴(x﹣3)(x﹣5)=0,
则x﹣3=0或x﹣5=0,
解得x1=3,x2=5,
当底边长为3,此时三边长度为2、2、3,能够成三角形,周长为7;
若底边长为5,此时三边长度为2、2、5,不能构成三角形;
故选:A.
3.某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示,则该班学生一周读书时间的中位数和众数分别是( )
读书时间(小时) 7 8 9 10 11
学生人数 6 6 8 12 8
A.9.5,10 B.9.5,12 C.9,10 D.9,12
【答案】A
【解答】解:由表格可得,
学生一共有:6+6+8+12+8=40(人),
故这组数据的中位数是(9+10)÷2=9.5,众数是10,
故选:A.
4.如图,△OAB∽△OCD,OA:OC=5:3,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A. B. C. D.
【答案】A
【解答】解:∵△OAB∽△OCD,OA:OC=5:3,
∴=,A正确;
∴=,B错误;
∴=,C错误;
∴OA:OC=5:2,D错误;
故选:A.
5.某快递公司今年一月份完成投递的快递总件数为10万件,二月份、三月份每月投递的件数逐月增加,第一季度总投递件数为33.1万件,问:二、三月份平均每月的增长率是多少?设平均每月增长的百分率为x,根据题意得方程( )
A.10(1+x)2=33.1
B.10(1+x)+10(1+x)2=33.1
C.10+10(1+x)2=33.1
D.10+10(1+x)+10(1+x)2=33.1
【答案】D
【解答】解:依题意,得:10+10(1+x)+10(1+x)2=33.1.
故选:D.
6.如图,将Rt△ABC平移到△A'B'C'的位置,其中∠C=90°使得点C'与△ABC的内心重合,已知AC=4,BC=3,则阴影部分的面积为( )
A. B. C. D.
【答案】D
【解答】解:如图,过点C'作C'E⊥AB,C'G⊥AC,C'H⊥BC,并延长C'E交A'B'于点F,连接AC',BC',CC',
∵点C'与△ABC的内心重合,C'E⊥AB,C'G⊥AC,C'H⊥BC,
∴C'E=C'G'=C'H,
∵S△ABC=S△AC'C+S△AC'B+S△BC'C,
∴AC×BC=AC×CC'+BA×C'E+BC×C'H
∴C'E=1,
∵将Rt△ABC平移到△A'B'C'的位置,
∴AB∥A'B',AB=A'B',A'C'=AC=4,B'C'=BC=3
∴C'F⊥A'B',A'B'=5
∴A'C'×B'C'=A'B'×C'F
∴C'F=
∵AB∥A'B'
∴△C'MN∽△C'A'B',
∴S阴影部分=S△C'A'B'×()2,
∴S阴影部分=×4×3×=
故选:D.
7.下列说法正确的是( )
A.若甲、乙两组数据的平均数相同,S甲2=0.1,S乙2=0.04,则乙组数据较稳定
B.如果明天降水的概率是50%,那么明天有半天都在降雨
C.了解全国中学生的节水意识应选用普查方式
D.早上的太阳从西方升起是必然事件
【答案】A
【解答】解:A、∵S甲2=0.1,S乙2=0.04,∴S甲2>S乙2,∴乙组数据较稳定,故本选项正确;
B、明天降雨的概率是50%表示降雨的可能性,故此选项错误;
C、了解全国中学生的节水意识应选用抽样调查方式,故本选项错误;
D、早上的太阳从西方升起是不可能事件,故本选项错误;
故选:A.
8.如图,菱形ABCD中,∠B=60°,AB=4,以AD为直径的⊙O交CD于点E,则劣弧的长为( )
A. B. C. D.
【答案】B
【解答】解:连接OE,如图所示:
∵四边形ABCD是菱形,
∴∠D=∠B=60°,AD=AB=4,
∴OA=OD=2,
∵OD=OE,
∴∠OED=∠D=60°,
∴∠DOE=180°﹣2×60°=60°,
∴劣弧的长==;
故选:B.
二.填空题(共8小题)
9.若3x=4y且xy≠0,则的值等于 .
【答案】.
【解答】解:∵3x=4y,
∴x=y,
当时,
,
故答案为:.
10.在某公益活动中,某社区对本社区的捐款情况进行了统计,如图是该社区捐款情况的条形统计图,则本次捐款金额的中位数是 200 元.
【答案】见试题解答内容
【解答】解:共有5+18+17+8=48人参加捐款,
将捐款金额从小到大排列,处在第24、25位的两个数都是200元,
因此中位数是200元,
故答案为:200.
11.如图,一张扇形纸片OAC,∠AOC=120°,OA=8,连接AB,BC,AC,若OA=AB,则图中阴影部分的面积为 (结果保留π).
【答案】.
【解答】解:∵OA=AB,OA=OB,
∴OA=OB=AB,
∴△AOB是等边三角形,
∴∠AOB=∠ABO=60°,
∵∠AOC=120°,
∴∠BOC=120°﹣60°=60°,
∴∠ABO=∠BOC=60°,
∴AB∥OC,
∴S△ABC=S△ABO,
∴S阴=S扇形AOB==.
故答案为.
12.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,则cosB= .
【答案】见试题解答内容
【解答】解:在Rt△ABC中,∠C=90°,
而BC=5,AC=12,
∴AB==13
而cosB==
故答案为.
13.明珠绿星数学社团想利用标杆测量楼高,小明先在N处竖立一根高1.6m的标杆MN,发现点B、M、P在同一直线上.测得PN=0.5m,AN=4.5m,已知,点A、N、P在同一直线上,MN⊥AP于点N,AB⊥AP于点A.则楼高AB为 16 m.
【答案】16.
【解答】解:∵MN⊥AP,AB⊥AP,
∴∠BAP=∠MNP=90°,
∵∠P=∠P,
∴△BAP∽△MNP,
∴=,
∴=,
解得:AB=16,
∴楼高AB为16m,
故答案为:16.
14.如图,在圆内接正六边形ABCDEF中,BD,EC交于点G,已知半径为,则EG的长为 2 .
【答案】2.
【解答】解:如图,连接BE、GO,
∵六边形ABCDEF为正六边形,
∴BE经过O点,且O是BE的中点,∠EDC==120°,∠EOG=90°,
∵DE=EC,
∴∠DEC=30°,
∵BC=CD,
∴=,
∴∠GEO=∠DEC=30°,
∴OG=EG,
由勾股定理得:OG2+OE2=EG2,即(EG)2+()2=EG2,
解得:EG=2.
故答案:2.
15.如图,一组平行横格线,其相邻横格线间的距离都相等,已知点A、B、C、D、O都在横格线上,且线段AD,BC交于点O,则AB:CD等于 2:3 .
【答案】见试题解答内容
【解答】解:如图,过点O作OE⊥AB于点E,OF⊥CD于点F,则E、O、F三点共线,
∵练习本中的横格线都平行,且相邻两条横格线间的距离都相等,
∴,
故答案为:2:3.
16.如图,在正方形方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB与CD相交于点P,则tan∠APC的值为 .
【答案】.
【解答】解:作AE∥CD交DE于点E,连接BE,如图所示,
∵CD∥AE,
∴∠APC=∠BAE,
设每个小正方形的边长为a,
由图可知:BE==a,
AE==2a,
AB==5a,
∴BE2+AE2=AB2,
∴△AEB是直角三角形,
∴tan∠BAE===,
∴tan∠APC=,
故答案为:.
三.解答题(共9小题)
17.解方程
(1)4(x﹣3)=2x(x﹣3);
(2)x2﹣4x﹣7=0.
【答案】(1)x1=3,x2=2;
(2)x1=2+,x2=2﹣.
【解答】解:(1)∵4(x﹣3)=2x(x﹣3),
∴4(x﹣3)﹣2x(x﹣3)=0,
则(x﹣3)(4﹣2x)=0,
∴x﹣3=0或4﹣2x=0,
解得x1=3,x2=2;
(2)∵x2﹣4x﹣7=0,
∴x2﹣4x=7,
则x2﹣4x+4=7+4,即(x﹣2)2=11,
∴x﹣2=±,
∴x1=2+,x2=2﹣.
18.2022年冬奥会在北京举办.现有如图所示“2022 北京冬梦之约”的四枚邮票供小明选择,依次记为A,B,C,D,背面完全相同.将这四枚邮票背面朝上,洗匀放好.
(1)小明从中随机抽取一枚,恰好抽到是B(冰墩墩)概率是 .
(2)小颖从中随机抽取一枚不放回,再从中随机抽取一枚.请用列表或画树状图的方法,求小颖同学抽到的两枚邮票恰好是B(冰墩墩)和C(雪容融)的概率.
【答案】(1).
(2).
【解答】解:(1)由题意可知,共有四种等可能的情况,
∴P(抽到是B)=.
故答案为:.
(2)根据题意画树状图,如图所示,
从上图可以看出,共有12种等可能的情况,其中小颖同学抽到的两枚邮票恰好是B(冰墩墩)和C(雪容融)的情况有2种.
∴小颖同学抽到的两枚邮票恰好是B(冰墩墩)和C(雪容融)的概率为:P==.
19.某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家提供的鸡腿中分别随机抽取15个鸡腿,记录它们的质量(单位:g),并对数据进行整理、描述和分析,部分信息如下:
Ⅰ.甲加工厂鸡腿的质量(单位:g)如下:
甲 72 73 74 75 76 78 79
频数 1 1 5 3 3 1 1
Ⅱ.乙加工厂鸡腿的质量(单位:g)如下:
72 75 72 75 78 77 73 75 76 77 71 78 79 75
Ⅲ.甲、乙两家加工厂鸡腿质量的平均数、中位数、众数和方差如下:
平均数 众数 中位数 方差
甲 75 a b 3.07
乙 75 c 75 6
根据以上信息,回答下列问题:
(1)表格中的a= 74 ,b= 75 ,c= 75 ;
(2)你认为快餐公司应该选择哪家的鸡腿?请说明理由.
【答案】(1)74;75;75;
(2)选甲加工厂的鸡腿,理由见解答.
【解答】解:(1)由题意可知,甲加工厂15个鸡腿的质量中74g出现的次数最多,故众数a=74;
把甲加工厂15个鸡腿的质量从小到大排列.排在中间的数是75g,故中位数b=75;
乙加工厂15个鸡腿的质量中75g出现的次数最多,故众数c=75.
故答案为:74;75;75;
(2)选甲加工厂的鸡腿,理由如下:
∵甲、乙平均值一样,乙的方差比甲的大,甲更稳定,
∴选甲加工厂的鸡腿.
20.某小区有一块长21米,宽8米的矩形空地,如图所示.社区计划在其中修建两块完全相同的矩形绿地,并且两块绿地之间及四周都留有宽度为x米的人行通道.如果这两块绿地的面积之和为60平方米,人行通道的宽度应是多少米?
【答案】见试题解答内容
【解答】解:设人行道的宽度为x米,
由题意得(21﹣3x)(8﹣2x)=60,
解得:x1=2,x2=9(不合题意,舍去).
答:人行道的宽度为2米.
21.如图,已知AD AC=AB AE,∠DAE=∠BAC.求证:△DAB∽△EAC.
【答案】证明过程请看解答.
【解答】证明:∵AD AC=AB AE,
∴=,
∵∠DAE=∠BAC.
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠DAB=∠EAC,
∴△DAB∽△EAC.
22.洛阳市栾川县老君山景区的老子铜像,是目前世界上最高的老子铜像.某数学活动小组用学到的锐角三角函数的知识去测量老子铜像的高度.如图,铜像底座CE的高度为21m,他们在测量点A(与C在同一水平线上)测得底座最高点E的仰角为20°,沿AC方向前进24m到达测量点B,测得老子铜像顶部D的仰角为60°.求老子铜像DE的高度(结果精确到0.1m.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,≈1.73)
【答案】38.4m.
【解答】解:在Rt△ACE中,
∵tanA=,CE=21m,∠A=20°,
∴AC=
≈
≈58.33(m).
∵AC=BC+AB,AB=24m,
∴BC=AC﹣AB
≈58.33﹣24
=34.33(m).
在Rt△CDB中,
∵tan∠CBD=,∠CBD=60°,
∴CD=tan∠CBD CB
≈tan60°×34.33
=×34.33
≈1.73×34.33
=59.3909
≈59.4(m).
∴DE=CD﹣CE
≈59.4﹣21
=38.4(m).
答:老子铜像DE的高度为38.4m.
23.如图,AB为⊙O的直径,CD为弦,CD⊥AB于点E,连接DO并延长交⊙O于点F,连接AF交CD于点G,CG=AG,连接AC.
(1)求证:AC∥DF;
(2)若AB=12,求AC和GD的长.
【答案】(1)见解析过程;
(2)AC=6,DG=4.
【解答】(1)证明:∵AG=CG,
∴∠DCA=∠CAF,
∵=,
∴∠CAF=∠CDF,
∴∠ACD=∠CDF,
∴AC∥DF;
(2)解:如图,连接CO,
∵AB⊥CD,
∴=,CE=DE,
∵∠DCA=∠CAF,
∴=,
∴==,
∴∠AOD=∠AOC=∠COF,
∵DF是直径,
∴∠AOD=∠AOC=∠COF=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴AC=AO=6,∠CAO=60°,
∵CE⊥AO,
∴AE=EO=3,∠ACD=30°,
∴CE=3=DE,
∵AG2=GE2+AE2,
∴AG2=(3﹣AG)2+9,
∴AG=2,
∴GE=,
∴DG=4.
24.如图,在平行四边形ABCD中,AC、BD交于点O,又M、N分别是OA、OC的中点.
(1)求证:BM=DN;
(2)若AO=BD,试判断四边形MBND的形状,并证明你的结论.
【答案】见试题解答内容
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵M、N分别是OA、OC的中点,
∴OM=OA,ON=OC,
∴OM=ON,
∵OB=OD,
∴四边形MBND是平行四边形,
∴BM=DN;
(2)若AO=BD,四边形MBND为矩形,
证明:∵OM=ON=OA,OB=OD=BD,AO=BD,
∴OM=ON=OB=OD,
∴BD=MN,
∴四边形MBND为矩形.
25.如图,在等边△ABC中,D,E分别为AB,BC边上的点,DE=EF,∠DEF=60°.
(1)如图1,若点F在AC边上,求证:AD=CF;
(2)如图2,连CF.若∠FCB=30°,求证:AD=2BE;
(3)如图3,O是BC的中点,点H在△ABC内,∠BHC=120°,点M,N分别在CH,BH上,MO⊥NO,若∠CAM=α,直接写出∠BAN的度数(用含有α的式子表示).
【答案】(1)证明略;
(2)证明略;
(3)∠BAN=30°﹣α.
【解答】(1)证明:如图,连接DF,
∵DE=EF,∠DEF=60°,
∴△DEF是等边三角形,
∴DF=EF,
∵△ABC是等边三角形,
∴∠A=∠C=60°,
∵∠AFE=∠AFD+∠DFE=60°+∠AFD,
∠AFE=∠C+∠EFC=60°+∠FEC,
∴∠AFD=∠FEC,
∵∠A=∠C,DF=EF,
∴△ADF≌△CFE(AAS),
∴AD=CF;
(2)证明:如图,过点F作JK∥AC交AB于点J,交BC于点K,过点F作PI∥AB交AC于P,交BC于点I,连接DF,
∴∠BJK=∠BAC=∠BKJ=∠ACB=60°=∠ABC,
∠CPI=∠BAC=∠B=∠CIP=60°=∠ACB,
∴△BJK和△CPI是等边三角形,
∵∠DEF=60°,DE=EF,
∴△DEF是等边三角形,
由(1)中结论可知,△BDE≌△JFD≌KEF,
∴DJ=BE=FK,
∵AB∥PI,FK∥AC,
∴四边形AJFP是平行四边形,
∴AJ=PF,
∵∠FIK=∠FKI=60°,
∴FI=FK,
∵△CPI为等边三角形,∠FCB=30°,
∴∠FCI=∠FCP=30°,
∴CF平分∠PCI,
∵△CPI是等边三角形,
∴FI=FP,
∵FP=AJ,
FK=BE=DJ,FI=FK,
∴AJ=DJ=BE,即AD=AJ+DJ=2BE;
(3)解:如图,延长MO到点G,使OG=OM,连接NG,BG,NM,作∠ACQ=∠ABN,且使CQ=BN,连接MQ,AQ,
∵MO⊥NO,OM=OG,
∴NG=MN,
∵MO=OG,BO=OC,∠MOC=∠BOG,
∴△BOG≌△COM(SAS),
∴BG=CM,∠GBO=∠OCM,
∴BG∥CM,
∴∠NBG=180°﹣∠BHC=60°,
∵BHC=120°,
∴∠HBC+∠HCB=60°,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,
∴∠ABH+∠HBC=∠ACH+∠HCB=60°,
∴∠ABH=∠HCB,∠HBC=∠ACH,
∵∠ACQ=∠ABN,AB=AC,BN=CQ,
∴△ACQ≌△ABN(SAS),
∴AN=AQ,∠BAN=∠CAQ,
∵∠ACB=∠ACH+∠BCH=60°,∠ABN=∠BCH=∠ACQ,
∴∠MCQ=∠ACM+∠ACQ=∠ACH+∠BCH=60°=∠NBG,
∵BN=CQ,BG=CM,
∴△BNG≌△CQM(SAS),
∴NG=MQ,
∵NG=NM,
∴MQ=MN,
∵AN=AQ,AM=AM,
∴△NAM≌△QAM(SSS),
∴∠NAM=∠MAQ=∠CAM+∠CAQ=∠CAM+∠BAN,
又∵∠NAM+∠CAM+∠BAN=60°,
∴∠CAM+∠BAN=30°,
∴∠CAM=α,
∴∠BAN=30°﹣α.
第1页(共1页)
一.选择题(共8小题)
1.如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
A. B. C. D.
2.等腰三角形的腰长为2,底边长是方程x2﹣8x+15=0的根,则三角形的周长为( )
A.7 B.9 C.10 D.7或9
3.某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示,则该班学生一周读书时间的中位数和众数分别是( )
读书时间(小时) 7 8 9 10 11
学生人数 6 6 8 12 8
A.9.5,10 B.9.5,12 C.9,10 D.9,12
4.如图,△OAB∽△OCD,OA:OC=5:3,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A. B. C. D.
5.某快递公司今年一月份完成投递的快递总件数为10万件,二月份、三月份每月投递的件数逐月增加,第一季度总投递件数为33.1万件,问:二、三月份平均每月的增长率是多少?设平均每月增长的百分率为x,根据题意得方程( )
A.10(1+x)2=33.1
B.10(1+x)+10(1+x)2=33.1
C.10+10(1+x)2=33.1
D.10+10(1+x)+10(1+x)2=33.1
6.如图,将Rt△ABC平移到△A'B'C'的位置,其中∠C=90°使得点C'与△ABC的内心重合,已知AC=4,BC=3,则阴影部分的面积为( )
A. B. C. D.
7.下列说法正确的是( )
A.若甲、乙两组数据的平均数相同,S甲2=0.1,S乙2=0.04,则乙组数据较稳定
B.如果明天降水的概率是50%,那么明天有半天都在降雨
C.了解全国中学生的节水意识应选用普查方式
D.早上的太阳从西方升起是必然事件
8.如图,菱形ABCD中,∠B=60°,AB=4,以AD为直径的⊙O交CD于点E,则劣弧的长为( )
A. B. C. D.
二.填空题(共8小题)
9.若3x=4y且xy≠0,则的值等于 .
10.在某公益活动中,某社区对本社区的捐款情况进行了统计,如图是该社区捐款情况的条形统计图,则本次捐款金额的中位数是 元.
11.如图,一张扇形纸片OAC,∠AOC=120°,OA=8,连接AB,BC,AC,若OA=AB,则图中阴影部分的面积为 (结果保留π).
12.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,则cosB= .
13.明珠绿星数学社团想利用标杆测量楼高,小明先在N处竖立一根高1.6m的标杆MN,发现点B、M、P在同一直线上.测得PN=0.5m,AN=4.5m,已知,点A、N、P在同一直线上,MN⊥AP于点N,AB⊥AP于点A.则楼高AB为 m.
14.如图,在圆内接正六边形ABCDEF中,BD,EC交于点G,已知半径为,则EG的长为 .
15.如图,一组平行横格线,其相邻横格线间的距离都相等,已知点A、B、C、D、O都在横格线上,且线段AD,BC交于点O,则AB:CD等于 .
16.如图,在正方形方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB与CD相交于点P,则tan∠APC的值为 .
三.解答题(共9小题)
17.解方程
(1)4(x﹣3)=2x(x﹣3);
(2)x2﹣4x﹣7=0.
18.2022年冬奥会在北京举办.现有如图所示“2022 北京冬梦之约”的四枚邮票供小明选择,依次记为A,B,C,D,背面完全相同.将这四枚邮票背面朝上,洗匀放好.
(1)小明从中随机抽取一枚,恰好抽到是B(冰墩墩)概率是 .
(2)小颖从中随机抽取一枚不放回,再从中随机抽取一枚.请用列表或画树状图的方法,求小颖同学抽到的两枚邮票恰好是B(冰墩墩)和C(雪容融)的概率.
19.某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家提供的鸡腿中分别随机抽取15个鸡腿,记录它们的质量(单位:g),并对数据进行整理、描述和分析,部分信息如下:
Ⅰ.甲加工厂鸡腿的质量(单位:g)如下:
甲 72 73 74 75 76 78 79
频数 1 1 5 3 3 1 1
Ⅱ.乙加工厂鸡腿的质量(单位:g)如下:
72 75 72 75 78 77 73 75 76 77 71 78 79 75
Ⅲ.甲、乙两家加工厂鸡腿质量的平均数、中位数、众数和方差如下:
平均数 众数 中位数 方差
甲 75 a b 3.07
乙 75 c 75 6
根据以上信息,回答下列问题:
(1)表格中的a= ,b= ,c= ;
(2)你认为快餐公司应该选择哪家的鸡腿?请说明理由.
20.某小区有一块长21米,宽8米的矩形空地,如图所示.社区计划在其中修建两块完全相同的矩形绿地,并且两块绿地之间及四周都留有宽度为x米的人行通道.如果这两块绿地的面积之和为60平方米,人行通道的宽度应是多少米?
21.如图,已知AD AC=AB AE,∠DAE=∠BAC.求证:△DAB∽△EAC.
22.洛阳市栾川县老君山景区的老子铜像,是目前世界上最高的老子铜像.某数学活动小组用学到的锐角三角函数的知识去测量老子铜像的高度.如图,铜像底座CE的高度为21m,他们在测量点A(与C在同一水平线上)测得底座最高点E的仰角为20°,沿AC方向前进24m到达测量点B,测得老子铜像顶部D的仰角为60°.求老子铜像DE的高度(结果精确到0.1m.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,≈1.73)
23.如图,AB为⊙O的直径,CD为弦,CD⊥AB于点E,连接DO并延长交⊙O于点F,连接AF交CD于点G,CG=AG,连接AC.
(1)求证:AC∥DF;
(2)若AB=12,求AC和GD的长.
24.如图,在平行四边形ABCD中,AC、BD交于点O,又M、N分别是OA、OC的中点.
(1)求证:BM=DN;
(2)若AO=BD,试判断四边形MBND的形状,并证明你的结论.
25.如图,在等边△ABC中,D,E分别为AB,BC边上的点,DE=EF,∠DEF=60°.
(1)如图1,若点F在AC边上,求证:AD=CF;
(2)如图2,连CF.若∠FCB=30°,求证:AD=2BE;
(3)如图3,O是BC的中点,点H在△ABC内,∠BHC=120°,点M,N分别在CH,BH上,MO⊥NO,若∠CAM=α,直接写出∠BAN的度数(用含有α的式子表示).
参考答案
一.选择题(共8小题)
1.如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
A. B. C. D.
【答案】D
【解答】解:连接BC,
由题意可得:OB=OC=BC,
则△OBC是等边三角形,
故sin∠AOC=sin60°=.
故选:D.
2.等腰三角形的腰长为2,底边长是方程x2﹣8x+15=0的根,则三角形的周长为( )
A.7 B.9 C.10 D.7或9
【答案】A
【解答】解:∵x2﹣8x+15=0,
∴(x﹣3)(x﹣5)=0,
则x﹣3=0或x﹣5=0,
解得x1=3,x2=5,
当底边长为3,此时三边长度为2、2、3,能够成三角形,周长为7;
若底边长为5,此时三边长度为2、2、5,不能构成三角形;
故选:A.
3.某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示,则该班学生一周读书时间的中位数和众数分别是( )
读书时间(小时) 7 8 9 10 11
学生人数 6 6 8 12 8
A.9.5,10 B.9.5,12 C.9,10 D.9,12
【答案】A
【解答】解:由表格可得,
学生一共有:6+6+8+12+8=40(人),
故这组数据的中位数是(9+10)÷2=9.5,众数是10,
故选:A.
4.如图,△OAB∽△OCD,OA:OC=5:3,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A. B. C. D.
【答案】A
【解答】解:∵△OAB∽△OCD,OA:OC=5:3,
∴=,A正确;
∴=,B错误;
∴=,C错误;
∴OA:OC=5:2,D错误;
故选:A.
5.某快递公司今年一月份完成投递的快递总件数为10万件,二月份、三月份每月投递的件数逐月增加,第一季度总投递件数为33.1万件,问:二、三月份平均每月的增长率是多少?设平均每月增长的百分率为x,根据题意得方程( )
A.10(1+x)2=33.1
B.10(1+x)+10(1+x)2=33.1
C.10+10(1+x)2=33.1
D.10+10(1+x)+10(1+x)2=33.1
【答案】D
【解答】解:依题意,得:10+10(1+x)+10(1+x)2=33.1.
故选:D.
6.如图,将Rt△ABC平移到△A'B'C'的位置,其中∠C=90°使得点C'与△ABC的内心重合,已知AC=4,BC=3,则阴影部分的面积为( )
A. B. C. D.
【答案】D
【解答】解:如图,过点C'作C'E⊥AB,C'G⊥AC,C'H⊥BC,并延长C'E交A'B'于点F,连接AC',BC',CC',
∵点C'与△ABC的内心重合,C'E⊥AB,C'G⊥AC,C'H⊥BC,
∴C'E=C'G'=C'H,
∵S△ABC=S△AC'C+S△AC'B+S△BC'C,
∴AC×BC=AC×CC'+BA×C'E+BC×C'H
∴C'E=1,
∵将Rt△ABC平移到△A'B'C'的位置,
∴AB∥A'B',AB=A'B',A'C'=AC=4,B'C'=BC=3
∴C'F⊥A'B',A'B'=5
∴A'C'×B'C'=A'B'×C'F
∴C'F=
∵AB∥A'B'
∴△C'MN∽△C'A'B',
∴S阴影部分=S△C'A'B'×()2,
∴S阴影部分=×4×3×=
故选:D.
7.下列说法正确的是( )
A.若甲、乙两组数据的平均数相同,S甲2=0.1,S乙2=0.04,则乙组数据较稳定
B.如果明天降水的概率是50%,那么明天有半天都在降雨
C.了解全国中学生的节水意识应选用普查方式
D.早上的太阳从西方升起是必然事件
【答案】A
【解答】解:A、∵S甲2=0.1,S乙2=0.04,∴S甲2>S乙2,∴乙组数据较稳定,故本选项正确;
B、明天降雨的概率是50%表示降雨的可能性,故此选项错误;
C、了解全国中学生的节水意识应选用抽样调查方式,故本选项错误;
D、早上的太阳从西方升起是不可能事件,故本选项错误;
故选:A.
8.如图,菱形ABCD中,∠B=60°,AB=4,以AD为直径的⊙O交CD于点E,则劣弧的长为( )
A. B. C. D.
【答案】B
【解答】解:连接OE,如图所示:
∵四边形ABCD是菱形,
∴∠D=∠B=60°,AD=AB=4,
∴OA=OD=2,
∵OD=OE,
∴∠OED=∠D=60°,
∴∠DOE=180°﹣2×60°=60°,
∴劣弧的长==;
故选:B.
二.填空题(共8小题)
9.若3x=4y且xy≠0,则的值等于 .
【答案】.
【解答】解:∵3x=4y,
∴x=y,
当时,
,
故答案为:.
10.在某公益活动中,某社区对本社区的捐款情况进行了统计,如图是该社区捐款情况的条形统计图,则本次捐款金额的中位数是 200 元.
【答案】见试题解答内容
【解答】解:共有5+18+17+8=48人参加捐款,
将捐款金额从小到大排列,处在第24、25位的两个数都是200元,
因此中位数是200元,
故答案为:200.
11.如图,一张扇形纸片OAC,∠AOC=120°,OA=8,连接AB,BC,AC,若OA=AB,则图中阴影部分的面积为 (结果保留π).
【答案】.
【解答】解:∵OA=AB,OA=OB,
∴OA=OB=AB,
∴△AOB是等边三角形,
∴∠AOB=∠ABO=60°,
∵∠AOC=120°,
∴∠BOC=120°﹣60°=60°,
∴∠ABO=∠BOC=60°,
∴AB∥OC,
∴S△ABC=S△ABO,
∴S阴=S扇形AOB==.
故答案为.
12.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,则cosB= .
【答案】见试题解答内容
【解答】解:在Rt△ABC中,∠C=90°,
而BC=5,AC=12,
∴AB==13
而cosB==
故答案为.
13.明珠绿星数学社团想利用标杆测量楼高,小明先在N处竖立一根高1.6m的标杆MN,发现点B、M、P在同一直线上.测得PN=0.5m,AN=4.5m,已知,点A、N、P在同一直线上,MN⊥AP于点N,AB⊥AP于点A.则楼高AB为 16 m.
【答案】16.
【解答】解:∵MN⊥AP,AB⊥AP,
∴∠BAP=∠MNP=90°,
∵∠P=∠P,
∴△BAP∽△MNP,
∴=,
∴=,
解得:AB=16,
∴楼高AB为16m,
故答案为:16.
14.如图,在圆内接正六边形ABCDEF中,BD,EC交于点G,已知半径为,则EG的长为 2 .
【答案】2.
【解答】解:如图,连接BE、GO,
∵六边形ABCDEF为正六边形,
∴BE经过O点,且O是BE的中点,∠EDC==120°,∠EOG=90°,
∵DE=EC,
∴∠DEC=30°,
∵BC=CD,
∴=,
∴∠GEO=∠DEC=30°,
∴OG=EG,
由勾股定理得:OG2+OE2=EG2,即(EG)2+()2=EG2,
解得:EG=2.
故答案:2.
15.如图,一组平行横格线,其相邻横格线间的距离都相等,已知点A、B、C、D、O都在横格线上,且线段AD,BC交于点O,则AB:CD等于 2:3 .
【答案】见试题解答内容
【解答】解:如图,过点O作OE⊥AB于点E,OF⊥CD于点F,则E、O、F三点共线,
∵练习本中的横格线都平行,且相邻两条横格线间的距离都相等,
∴,
故答案为:2:3.
16.如图,在正方形方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB与CD相交于点P,则tan∠APC的值为 .
【答案】.
【解答】解:作AE∥CD交DE于点E,连接BE,如图所示,
∵CD∥AE,
∴∠APC=∠BAE,
设每个小正方形的边长为a,
由图可知:BE==a,
AE==2a,
AB==5a,
∴BE2+AE2=AB2,
∴△AEB是直角三角形,
∴tan∠BAE===,
∴tan∠APC=,
故答案为:.
三.解答题(共9小题)
17.解方程
(1)4(x﹣3)=2x(x﹣3);
(2)x2﹣4x﹣7=0.
【答案】(1)x1=3,x2=2;
(2)x1=2+,x2=2﹣.
【解答】解:(1)∵4(x﹣3)=2x(x﹣3),
∴4(x﹣3)﹣2x(x﹣3)=0,
则(x﹣3)(4﹣2x)=0,
∴x﹣3=0或4﹣2x=0,
解得x1=3,x2=2;
(2)∵x2﹣4x﹣7=0,
∴x2﹣4x=7,
则x2﹣4x+4=7+4,即(x﹣2)2=11,
∴x﹣2=±,
∴x1=2+,x2=2﹣.
18.2022年冬奥会在北京举办.现有如图所示“2022 北京冬梦之约”的四枚邮票供小明选择,依次记为A,B,C,D,背面完全相同.将这四枚邮票背面朝上,洗匀放好.
(1)小明从中随机抽取一枚,恰好抽到是B(冰墩墩)概率是 .
(2)小颖从中随机抽取一枚不放回,再从中随机抽取一枚.请用列表或画树状图的方法,求小颖同学抽到的两枚邮票恰好是B(冰墩墩)和C(雪容融)的概率.
【答案】(1).
(2).
【解答】解:(1)由题意可知,共有四种等可能的情况,
∴P(抽到是B)=.
故答案为:.
(2)根据题意画树状图,如图所示,
从上图可以看出,共有12种等可能的情况,其中小颖同学抽到的两枚邮票恰好是B(冰墩墩)和C(雪容融)的情况有2种.
∴小颖同学抽到的两枚邮票恰好是B(冰墩墩)和C(雪容融)的概率为:P==.
19.某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家提供的鸡腿中分别随机抽取15个鸡腿,记录它们的质量(单位:g),并对数据进行整理、描述和分析,部分信息如下:
Ⅰ.甲加工厂鸡腿的质量(单位:g)如下:
甲 72 73 74 75 76 78 79
频数 1 1 5 3 3 1 1
Ⅱ.乙加工厂鸡腿的质量(单位:g)如下:
72 75 72 75 78 77 73 75 76 77 71 78 79 75
Ⅲ.甲、乙两家加工厂鸡腿质量的平均数、中位数、众数和方差如下:
平均数 众数 中位数 方差
甲 75 a b 3.07
乙 75 c 75 6
根据以上信息,回答下列问题:
(1)表格中的a= 74 ,b= 75 ,c= 75 ;
(2)你认为快餐公司应该选择哪家的鸡腿?请说明理由.
【答案】(1)74;75;75;
(2)选甲加工厂的鸡腿,理由见解答.
【解答】解:(1)由题意可知,甲加工厂15个鸡腿的质量中74g出现的次数最多,故众数a=74;
把甲加工厂15个鸡腿的质量从小到大排列.排在中间的数是75g,故中位数b=75;
乙加工厂15个鸡腿的质量中75g出现的次数最多,故众数c=75.
故答案为:74;75;75;
(2)选甲加工厂的鸡腿,理由如下:
∵甲、乙平均值一样,乙的方差比甲的大,甲更稳定,
∴选甲加工厂的鸡腿.
20.某小区有一块长21米,宽8米的矩形空地,如图所示.社区计划在其中修建两块完全相同的矩形绿地,并且两块绿地之间及四周都留有宽度为x米的人行通道.如果这两块绿地的面积之和为60平方米,人行通道的宽度应是多少米?
【答案】见试题解答内容
【解答】解:设人行道的宽度为x米,
由题意得(21﹣3x)(8﹣2x)=60,
解得:x1=2,x2=9(不合题意,舍去).
答:人行道的宽度为2米.
21.如图,已知AD AC=AB AE,∠DAE=∠BAC.求证:△DAB∽△EAC.
【答案】证明过程请看解答.
【解答】证明:∵AD AC=AB AE,
∴=,
∵∠DAE=∠BAC.
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠DAB=∠EAC,
∴△DAB∽△EAC.
22.洛阳市栾川县老君山景区的老子铜像,是目前世界上最高的老子铜像.某数学活动小组用学到的锐角三角函数的知识去测量老子铜像的高度.如图,铜像底座CE的高度为21m,他们在测量点A(与C在同一水平线上)测得底座最高点E的仰角为20°,沿AC方向前进24m到达测量点B,测得老子铜像顶部D的仰角为60°.求老子铜像DE的高度(结果精确到0.1m.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,≈1.73)
【答案】38.4m.
【解答】解:在Rt△ACE中,
∵tanA=,CE=21m,∠A=20°,
∴AC=
≈
≈58.33(m).
∵AC=BC+AB,AB=24m,
∴BC=AC﹣AB
≈58.33﹣24
=34.33(m).
在Rt△CDB中,
∵tan∠CBD=,∠CBD=60°,
∴CD=tan∠CBD CB
≈tan60°×34.33
=×34.33
≈1.73×34.33
=59.3909
≈59.4(m).
∴DE=CD﹣CE
≈59.4﹣21
=38.4(m).
答:老子铜像DE的高度为38.4m.
23.如图,AB为⊙O的直径,CD为弦,CD⊥AB于点E,连接DO并延长交⊙O于点F,连接AF交CD于点G,CG=AG,连接AC.
(1)求证:AC∥DF;
(2)若AB=12,求AC和GD的长.
【答案】(1)见解析过程;
(2)AC=6,DG=4.
【解答】(1)证明:∵AG=CG,
∴∠DCA=∠CAF,
∵=,
∴∠CAF=∠CDF,
∴∠ACD=∠CDF,
∴AC∥DF;
(2)解:如图,连接CO,
∵AB⊥CD,
∴=,CE=DE,
∵∠DCA=∠CAF,
∴=,
∴==,
∴∠AOD=∠AOC=∠COF,
∵DF是直径,
∴∠AOD=∠AOC=∠COF=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴AC=AO=6,∠CAO=60°,
∵CE⊥AO,
∴AE=EO=3,∠ACD=30°,
∴CE=3=DE,
∵AG2=GE2+AE2,
∴AG2=(3﹣AG)2+9,
∴AG=2,
∴GE=,
∴DG=4.
24.如图,在平行四边形ABCD中,AC、BD交于点O,又M、N分别是OA、OC的中点.
(1)求证:BM=DN;
(2)若AO=BD,试判断四边形MBND的形状,并证明你的结论.
【答案】见试题解答内容
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵M、N分别是OA、OC的中点,
∴OM=OA,ON=OC,
∴OM=ON,
∵OB=OD,
∴四边形MBND是平行四边形,
∴BM=DN;
(2)若AO=BD,四边形MBND为矩形,
证明:∵OM=ON=OA,OB=OD=BD,AO=BD,
∴OM=ON=OB=OD,
∴BD=MN,
∴四边形MBND为矩形.
25.如图,在等边△ABC中,D,E分别为AB,BC边上的点,DE=EF,∠DEF=60°.
(1)如图1,若点F在AC边上,求证:AD=CF;
(2)如图2,连CF.若∠FCB=30°,求证:AD=2BE;
(3)如图3,O是BC的中点,点H在△ABC内,∠BHC=120°,点M,N分别在CH,BH上,MO⊥NO,若∠CAM=α,直接写出∠BAN的度数(用含有α的式子表示).
【答案】(1)证明略;
(2)证明略;
(3)∠BAN=30°﹣α.
【解答】(1)证明:如图,连接DF,
∵DE=EF,∠DEF=60°,
∴△DEF是等边三角形,
∴DF=EF,
∵△ABC是等边三角形,
∴∠A=∠C=60°,
∵∠AFE=∠AFD+∠DFE=60°+∠AFD,
∠AFE=∠C+∠EFC=60°+∠FEC,
∴∠AFD=∠FEC,
∵∠A=∠C,DF=EF,
∴△ADF≌△CFE(AAS),
∴AD=CF;
(2)证明:如图,过点F作JK∥AC交AB于点J,交BC于点K,过点F作PI∥AB交AC于P,交BC于点I,连接DF,
∴∠BJK=∠BAC=∠BKJ=∠ACB=60°=∠ABC,
∠CPI=∠BAC=∠B=∠CIP=60°=∠ACB,
∴△BJK和△CPI是等边三角形,
∵∠DEF=60°,DE=EF,
∴△DEF是等边三角形,
由(1)中结论可知,△BDE≌△JFD≌KEF,
∴DJ=BE=FK,
∵AB∥PI,FK∥AC,
∴四边形AJFP是平行四边形,
∴AJ=PF,
∵∠FIK=∠FKI=60°,
∴FI=FK,
∵△CPI为等边三角形,∠FCB=30°,
∴∠FCI=∠FCP=30°,
∴CF平分∠PCI,
∵△CPI是等边三角形,
∴FI=FP,
∵FP=AJ,
FK=BE=DJ,FI=FK,
∴AJ=DJ=BE,即AD=AJ+DJ=2BE;
(3)解:如图,延长MO到点G,使OG=OM,连接NG,BG,NM,作∠ACQ=∠ABN,且使CQ=BN,连接MQ,AQ,
∵MO⊥NO,OM=OG,
∴NG=MN,
∵MO=OG,BO=OC,∠MOC=∠BOG,
∴△BOG≌△COM(SAS),
∴BG=CM,∠GBO=∠OCM,
∴BG∥CM,
∴∠NBG=180°﹣∠BHC=60°,
∵BHC=120°,
∴∠HBC+∠HCB=60°,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,
∴∠ABH+∠HBC=∠ACH+∠HCB=60°,
∴∠ABH=∠HCB,∠HBC=∠ACH,
∵∠ACQ=∠ABN,AB=AC,BN=CQ,
∴△ACQ≌△ABN(SAS),
∴AN=AQ,∠BAN=∠CAQ,
∵∠ACB=∠ACH+∠BCH=60°,∠ABN=∠BCH=∠ACQ,
∴∠MCQ=∠ACM+∠ACQ=∠ACH+∠BCH=60°=∠NBG,
∵BN=CQ,BG=CM,
∴△BNG≌△CQM(SAS),
∴NG=MQ,
∵NG=NM,
∴MQ=MN,
∵AN=AQ,AM=AM,
∴△NAM≌△QAM(SSS),
∴∠NAM=∠MAQ=∠CAM+∠CAQ=∠CAM+∠BAN,
又∵∠NAM+∠CAM+∠BAN=60°,
∴∠CAM+∠BAN=30°,
∴∠CAM=α,
∴∠BAN=30°﹣α.
第1页(共1页)
同课章节目录
