江苏省2023-2024学年上学期苏科版七年级数学第5章 走进图形世界(中考常考题)单元培优专题练习(含解析)
文档属性
| 名称 | 江苏省2023-2024学年上学期苏科版七年级数学第5章 走进图形世界(中考常考题)单元培优专题练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 709.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 16:45:41 | ||
图片预览



文档简介
第5章 走进图形世界(中考常考题)-江苏省2023-2024学年上学期七年级数学单元培优专题练习(苏科版)
一.选择题(共23小题)
1.(2023 盐城)由六块相同的小正方体搭成的几何体如图所示,则它的俯视图是( )
A. B. C. D.
2.(2023 扬州)下列图形是棱锥侧面展开图的是( )
A. B.
C. D.
3.(2023 淮安)如图是一个几何体的三视图,则该几何体的侧面积是( )
A.12π B.15π C.18π D.24π
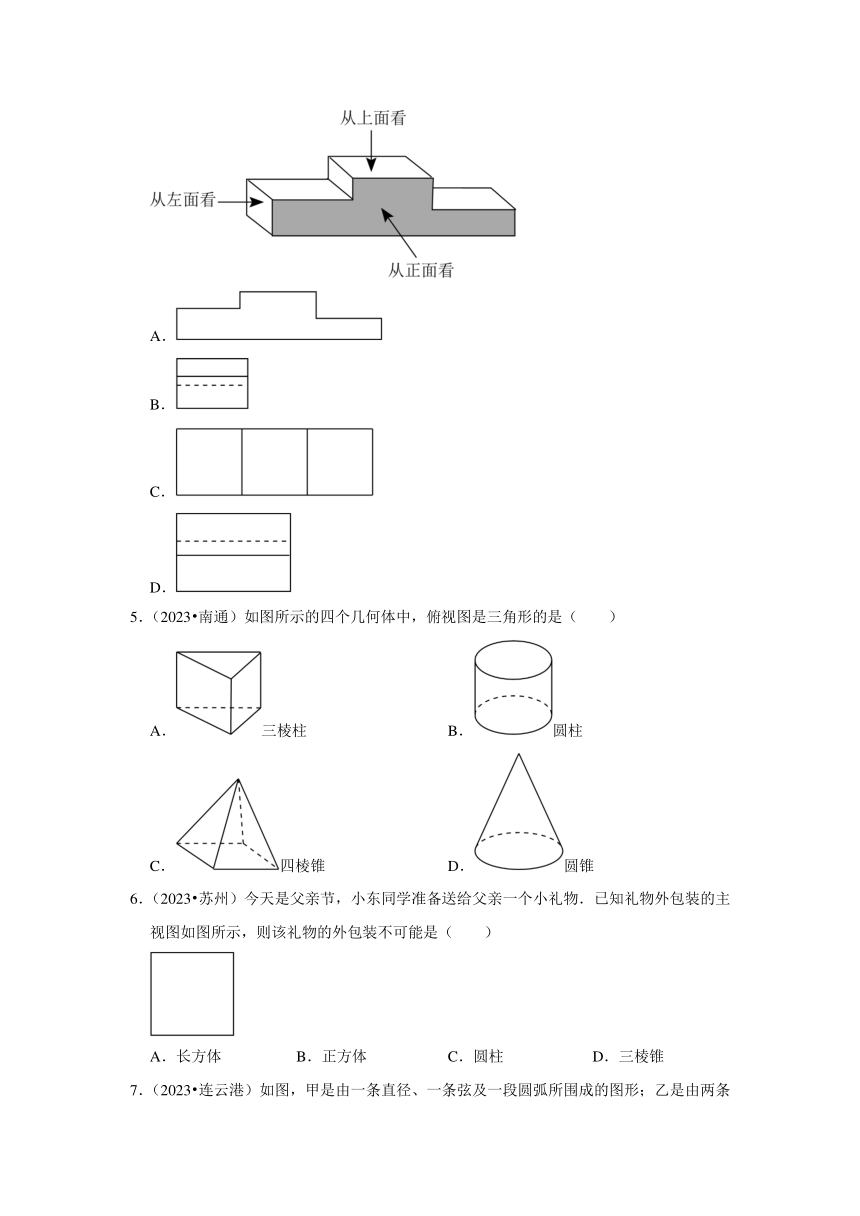
4.(2023 常州)运动场上的颁奖台如图所示,它的主视图是( )
A.
B.
C.
D.
5.(2023 南通)如图所示的四个几何体中,俯视图是三角形的是( )
A.三棱柱 B.圆柱
C.四棱锥 D.圆锥
6.(2023 苏州)今天是父亲节,小东同学准备送给父亲一个小礼物.已知礼物外包装的主视图如图所示,则该礼物的外包装不可能是( )
A.长方体 B.正方体 C.圆柱 D.三棱锥
7.(2023 连云港)如图,甲是由一条直径、一条弦及一段圆弧所围成的图形;乙是由两条半径与一段圆弧所围成的图形;丙是由不过圆心O的两条线段与一段圆弧所围成的图形.下列叙述正确的是( )
A.只有甲是扇形 B.只有乙是扇形
C.只有丙是扇形 D.只有乙、丙是扇形
8.(2023 连云港)下列水平放置的几何体中,主视图是圆形的是( )
A. B.
C. D.
9.(2022 泰州)如图为一个几何体的表面展开图,则该几何体是( )
A.三棱锥 B.四棱锥 C.四棱柱 D.圆锥
10.(2022 徐州)如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A. B.
C. D.
11.(2022 常州)下列图形中,为圆柱的侧面展开图的是( )
A. B.
C. D.
12.(2022 宿迁)下列展开图中,是正方体展开图的是( )
A. B.
C. D.
13.(2022 扬州)如图是某一几何体的主视图、左视图、俯视图,该几何体是( )
A.四棱柱 B.四棱锥 C.三棱柱 D.三棱锥
14.(2022 南通)如图是由5个相同的正方体搭成的立体图形,则它的主视图为( )
A. B. C. D.
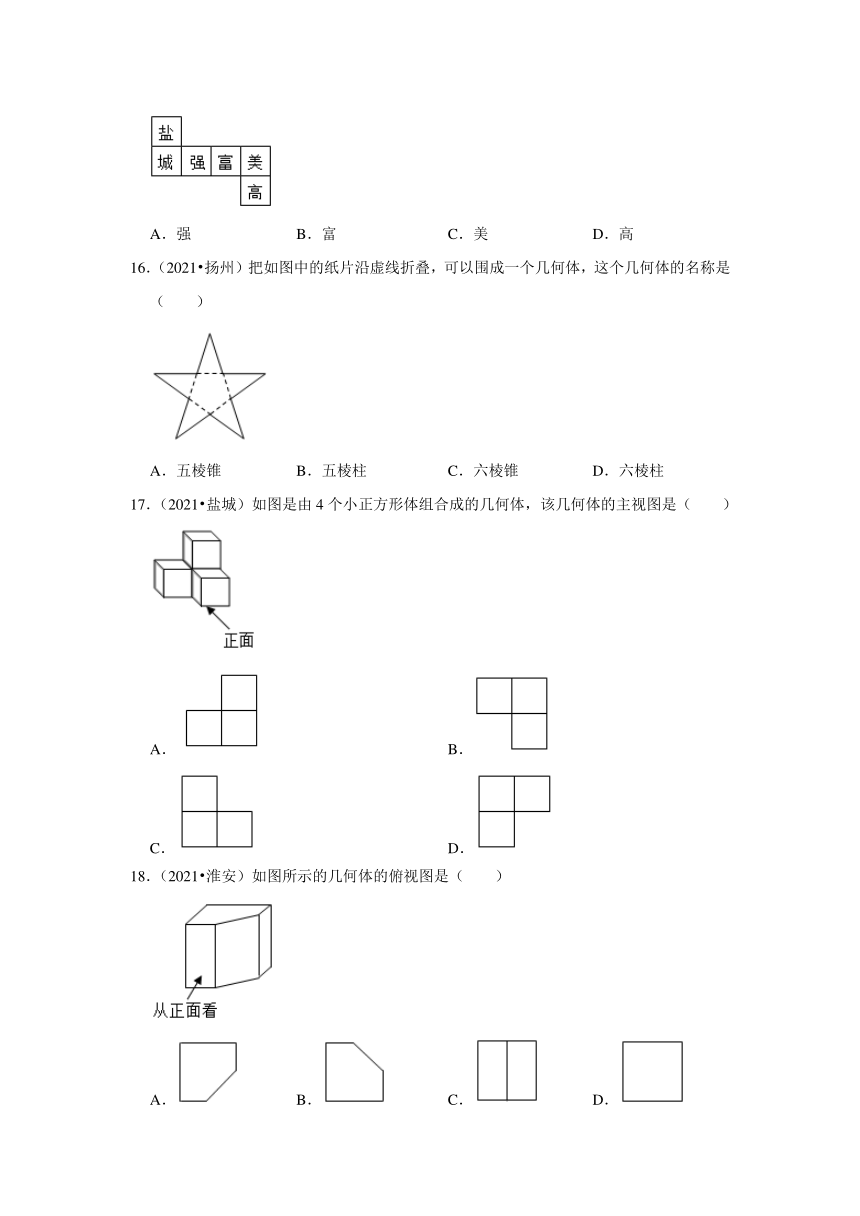
15.(2022 盐城)正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( )
A.强 B.富 C.美 D.高
16.(2021 扬州)把如图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )
A.五棱锥 B.五棱柱 C.六棱锥 D.六棱柱
17.(2021 盐城)如图是由4个小正方形体组合成的几何体,该几何体的主视图是( )
A. B.
C. D.
18.(2021 淮安)如图所示的几何体的俯视图是( )
A. B. C. D.
19.(2021 镇江)如图所示,该几何体的俯视图是( )
A.正方形 B.长方形 C.三角形 D.圆
20.(2021 泰州)如图所示几何体的左视图是( )
A. B.
C. D.
21.(2021 南通)如图,根据三视图,这个立体图形的名称是( )
A.三棱柱 B.圆柱 C.三棱锥 D.圆锥
22.(2021 苏州)如图,圆锥的主视图是( )
A. B.
C. D.
23.(2021 常州)如图是某几何体的三视图,该几何体是( )
A.正方体 B.圆锥 C.圆柱 D.球
二.填空题(共2小题)
24.(2023 常州)若圆柱的底面半径和高均为a,则它的体积是 (用含a的代数式表示).
25.(2023 无锡)若直三棱柱的上下底面为正三角形,侧面展开图是边长为6的正方形,则该直三棱柱的表面积为 .
三.解答题(共1小题)
26.(2023 徐州)两汉文化看徐州,桐桐在徐州博物馆“天工汉玉”展厅参观时了解到;玉壁,玉环为我国的传统玉器,通常为正中带圆孔的扁圆型器物,据《尔雅 释器》记载:“肉倍好,谓之璧;肉好若一,调之环.”如图1,“肉”指边(阴影部分),“好”指孔,其比例关系见图示,以考古发现来看,这两种玉器的“肉”与“好”未必符合该比例关系.
(1)若图1中两个大圆的直径相等,则璧与环的“肉”的面积之比为 ;
(2)利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法):
①图2为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图,试判断该件玉器的比例关系是否符合“肉好若一”?
②图3表示一件圆形玉坯,若将其加工成玉璧,且比例关系符合“肉倍好”,请画出内孔.
第5章 走进图形世界(中考常考题)-江苏省2023-2024学年上学期七年级数学单元培优专题练习(苏科版)
参考答案与试题解析
一.选择题(共23小题)
1.(2023 盐城)由六块相同的小正方体搭成的几何体如图所示,则它的俯视图是( )
A. B. C. D.
【答案】D
【解答】解:俯视图有3列,从左到右小正方形的个数是2,1,1,
故选:D.
2.(2023 扬州)下列图形是棱锥侧面展开图的是( )
A. B.
C. D.
【答案】D
【解答】解:四棱锥的侧面展开图是四个三角形.
故选:D.
3.(2023 淮安)如图是一个几何体的三视图,则该几何体的侧面积是( )
A.12π B.15π C.18π D.24π
【答案】B
【解答】解:由三视图可知此几何体为圆锥,
∵d=6,h=4,
∴圆锥的母线长为=5,
∴圆锥的侧面积为:×6π×5=15π,
故选:B.
4.(2023 常州)运动场上的颁奖台如图所示,它的主视图是( )
A.
B.
C.
D.
【答案】A
【解答】解:从正面看得到.
故选:A.
5.(2023 南通)如图所示的四个几何体中,俯视图是三角形的是( )
A.三棱柱 B.圆柱
C.四棱锥 D.圆锥
【答案】A
【解答】解:A.三棱柱的俯视图是三角形,故此选项符合题意;
B.圆柱体的俯视图是圆,故此选项不合题意;
C.四棱锥的俯视图是四边形(画有对角线),故此选项不合题意;
D.圆锥体的俯视图是圆(带圆心),故此选项不合题意.
故选:A.
6.(2023 苏州)今天是父亲节,小东同学准备送给父亲一个小礼物.已知礼物外包装的主视图如图所示,则该礼物的外包装不可能是( )
A.长方体 B.正方体 C.圆柱 D.三棱锥
【答案】D
【解答】解:根据主视图可知,只有D选项不可能.
故选:D.
7.(2023 连云港)如图,甲是由一条直径、一条弦及一段圆弧所围成的图形;乙是由两条半径与一段圆弧所围成的图形;丙是由不过圆心O的两条线段与一段圆弧所围成的图形.下列叙述正确的是( )
A.只有甲是扇形 B.只有乙是扇形
C.只有丙是扇形 D.只有乙、丙是扇形
【答案】B
【解答】解:由扇形的定义可知,只有乙是扇形,
故选:B.
8.(2023 连云港)下列水平放置的几何体中,主视图是圆形的是( )
A. B.
C. D.
【答案】C
【解答】解:A.主视图是三角形,故此选项不符合题意;
B.主视图是梯形,故此选项不合题意;
C.主视图是圆,故此选项符合题意;
D.主视图是矩形,故此选项不合题意;
故选:C.
9.(2022 泰州)如图为一个几何体的表面展开图,则该几何体是( )
A.三棱锥 B.四棱锥 C.四棱柱 D.圆锥
【答案】B
【解答】解:根据展开图可以得出是四棱锥的展开图,
故选:B.
10.(2022 徐州)如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A. B.
C. D.
【答案】D
【解答】解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,
A、1点6点是相对面,3点与5点是相对面,2点与4点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
B、4点与3点是相对面,2点与6点是相对面,1点与5点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
C、3点与4点是相对面,2点与6点是相对面,1点与5点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
D、2点与5点是相对面,3点与4点是相对面,1点与6点是相对面,所以可以折成符合规则的骰子,故本选项符合题意.
故选:D.
11.(2022 常州)下列图形中,为圆柱的侧面展开图的是( )
A. B.
C. D.
【答案】D
【解答】解:根据题意,把圆柱的侧面沿它的一条母线剪开展在一个平面上,
得到其侧面展开图是对边平行且相等的四边形;
又有母线垂直于上下底面,故可得是长方形.
故选:D.
12.(2022 宿迁)下列展开图中,是正方体展开图的是( )
A. B.
C. D.
【答案】C
【解答】解:由展开图的知识可知,四个小正方形绝对不可能展开成田字形,故A选项和D选项都不符合题意;
四个连成一排的小正方形可以围成前后左右四面,剩下的两面必须分在上下两面才能围成正方体,
故B选项不符合题意,C选项符合题意,
故选:C.
13.(2022 扬州)如图是某一几何体的主视图、左视图、俯视图,该几何体是( )
A.四棱柱 B.四棱锥 C.三棱柱 D.三棱锥
【答案】B
【解答】解:由于主视图与左视图是三角形,
俯视图是正方形,故该几何体是四棱锥,
故选:B.
14.(2022 南通)如图是由5个相同的正方体搭成的立体图形,则它的主视图为( )
A. B. C. D.
【答案】A
【解答】解:从正面看该组合体,所看到的图形与选项A中的图形相同,
故选:A.
15.(2022 盐城)正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( )
A.强 B.富 C.美 D.高
【答案】D
【解答】解:正方体的表面展开图相对的面之间一定相隔一个正方形,
“盐”与“高”是相对面,
“城”与“富”是相对面,
“强”与“美”是相对面,
故选:D.
16.(2021 扬州)把如图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )
A.五棱锥 B.五棱柱 C.六棱锥 D.六棱柱
【答案】A
【解答】解:由图可知:折叠后,该几何体的底面是五边形,
则该几何体为五棱锥,
故选:A.
17.(2021 盐城)如图是由4个小正方形体组合成的几何体,该几何体的主视图是( )
A. B.
C. D.
【答案】A
【解答】解:该组合体的主视图如下:
故选:A.
18.(2021 淮安)如图所示的几何体的俯视图是( )
A. B. C. D.
【答案】A
【解答】解:从上面看该几何体,所看到的图形如下:
故选:A.
19.(2021 镇江)如图所示,该几何体的俯视图是( )
A.正方形 B.长方形 C.三角形 D.圆
【答案】C
【解答】解:从上面看该几何体,所看到的图形是三角形.
故选:C.
20.(2021 泰州)如图所示几何体的左视图是( )
A. B.
C. D.
【答案】C
【解答】解:从左边看,是一列两个矩形.
故选:C.
21.(2021 南通)如图,根据三视图,这个立体图形的名称是( )
A.三棱柱 B.圆柱 C.三棱锥 D.圆锥
【答案】A
【解答】解:根据三视图可以得出立体图形是三棱柱,
故选:A.
22.(2021 苏州)如图,圆锥的主视图是( )
A. B.
C. D.
【答案】A
【解答】解:圆锥的主视图是一个等腰三角形,
故选:A.
23.(2021 常州)如图是某几何体的三视图,该几何体是( )
A.正方体 B.圆锥 C.圆柱 D.球
【答案】D
【解答】解:一个几何体的三视图都是圆,这个几何体是球.
故选:D.
二.填空题(共2小题)
24.(2023 常州)若圆柱的底面半径和高均为a,则它的体积是 πa3 (用含a的代数式表示).
【答案】πa3.
【解答】解:圆柱的底面半径和高均为a,则它的体积是πa2 a=πa3.
故答案为:πa3.
25.(2023 无锡)若直三棱柱的上下底面为正三角形,侧面展开图是边长为6的正方形,则该直三棱柱的表面积为 36+2 .
【答案】36.
【解答】解:依题意可知:直三棱柱的上下底面的正三角形的边长为2,
∴其2个底面积为=2.
∵侧面展开图是边长为6的正方形,
∴其侧面积为6×6=36,
∴该直三棱柱的表面积为36+2.
故答案为:36+2.
三.解答题(共1小题)
26.(2023 徐州)两汉文化看徐州,桐桐在徐州博物馆“天工汉玉”展厅参观时了解到;玉壁,玉环为我国的传统玉器,通常为正中带圆孔的扁圆型器物,据《尔雅 释器》记载:“肉倍好,谓之璧;肉好若一,调之环.”如图1,“肉”指边(阴影部分),“好”指孔,其比例关系见图示,以考古发现来看,这两种玉器的“肉”与“好”未必符合该比例关系.
(1)若图1中两个大圆的直径相等,则璧与环的“肉”的面积之比为 32:27 ;
(2)利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法):
①图2为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图,试判断该件玉器的比例关系是否符合“肉好若一”?
②图3表示一件圆形玉坯,若将其加工成玉璧,且比例关系符合“肉倍好”,请画出内孔.
【答案】(1)32:27;
(2)①见解析部分;
②见解析部分.
【解答】解:(1)由图1可知:璧的“肉”的面积为 π×(32﹣12)=8π;环的“肉”的面积为 π×(32﹣1.52)=6.75π,
∴它们的面积之比为 8 π:6.75 π=32:27;
故答案为32:27;
(2)①观察图象可知,不符合“肉好若一”关系;
②按照①中作出圆的圆心O,过圆心画一条直径AB,过点A作一条射线,然后以A为圆心,适当长为半 径画弧,把射线三等分,交点分别为C、D、E,连接BE,然后分别过点C、D作BE的平行线,交AB于 点F、G,进而以FG为直径画圆,则问题得解;如图所示:
一.选择题(共23小题)
1.(2023 盐城)由六块相同的小正方体搭成的几何体如图所示,则它的俯视图是( )
A. B. C. D.
2.(2023 扬州)下列图形是棱锥侧面展开图的是( )
A. B.
C. D.
3.(2023 淮安)如图是一个几何体的三视图,则该几何体的侧面积是( )
A.12π B.15π C.18π D.24π
4.(2023 常州)运动场上的颁奖台如图所示,它的主视图是( )
A.
B.
C.
D.
5.(2023 南通)如图所示的四个几何体中,俯视图是三角形的是( )
A.三棱柱 B.圆柱
C.四棱锥 D.圆锥
6.(2023 苏州)今天是父亲节,小东同学准备送给父亲一个小礼物.已知礼物外包装的主视图如图所示,则该礼物的外包装不可能是( )
A.长方体 B.正方体 C.圆柱 D.三棱锥
7.(2023 连云港)如图,甲是由一条直径、一条弦及一段圆弧所围成的图形;乙是由两条半径与一段圆弧所围成的图形;丙是由不过圆心O的两条线段与一段圆弧所围成的图形.下列叙述正确的是( )
A.只有甲是扇形 B.只有乙是扇形
C.只有丙是扇形 D.只有乙、丙是扇形
8.(2023 连云港)下列水平放置的几何体中,主视图是圆形的是( )
A. B.
C. D.
9.(2022 泰州)如图为一个几何体的表面展开图,则该几何体是( )
A.三棱锥 B.四棱锥 C.四棱柱 D.圆锥
10.(2022 徐州)如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A. B.
C. D.
11.(2022 常州)下列图形中,为圆柱的侧面展开图的是( )
A. B.
C. D.
12.(2022 宿迁)下列展开图中,是正方体展开图的是( )
A. B.
C. D.
13.(2022 扬州)如图是某一几何体的主视图、左视图、俯视图,该几何体是( )
A.四棱柱 B.四棱锥 C.三棱柱 D.三棱锥
14.(2022 南通)如图是由5个相同的正方体搭成的立体图形,则它的主视图为( )
A. B. C. D.
15.(2022 盐城)正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( )
A.强 B.富 C.美 D.高
16.(2021 扬州)把如图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )
A.五棱锥 B.五棱柱 C.六棱锥 D.六棱柱
17.(2021 盐城)如图是由4个小正方形体组合成的几何体,该几何体的主视图是( )
A. B.
C. D.
18.(2021 淮安)如图所示的几何体的俯视图是( )
A. B. C. D.
19.(2021 镇江)如图所示,该几何体的俯视图是( )
A.正方形 B.长方形 C.三角形 D.圆
20.(2021 泰州)如图所示几何体的左视图是( )
A. B.
C. D.
21.(2021 南通)如图,根据三视图,这个立体图形的名称是( )
A.三棱柱 B.圆柱 C.三棱锥 D.圆锥
22.(2021 苏州)如图,圆锥的主视图是( )
A. B.
C. D.
23.(2021 常州)如图是某几何体的三视图,该几何体是( )
A.正方体 B.圆锥 C.圆柱 D.球
二.填空题(共2小题)
24.(2023 常州)若圆柱的底面半径和高均为a,则它的体积是 (用含a的代数式表示).
25.(2023 无锡)若直三棱柱的上下底面为正三角形,侧面展开图是边长为6的正方形,则该直三棱柱的表面积为 .
三.解答题(共1小题)
26.(2023 徐州)两汉文化看徐州,桐桐在徐州博物馆“天工汉玉”展厅参观时了解到;玉壁,玉环为我国的传统玉器,通常为正中带圆孔的扁圆型器物,据《尔雅 释器》记载:“肉倍好,谓之璧;肉好若一,调之环.”如图1,“肉”指边(阴影部分),“好”指孔,其比例关系见图示,以考古发现来看,这两种玉器的“肉”与“好”未必符合该比例关系.
(1)若图1中两个大圆的直径相等,则璧与环的“肉”的面积之比为 ;
(2)利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法):
①图2为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图,试判断该件玉器的比例关系是否符合“肉好若一”?
②图3表示一件圆形玉坯,若将其加工成玉璧,且比例关系符合“肉倍好”,请画出内孔.
第5章 走进图形世界(中考常考题)-江苏省2023-2024学年上学期七年级数学单元培优专题练习(苏科版)
参考答案与试题解析
一.选择题(共23小题)
1.(2023 盐城)由六块相同的小正方体搭成的几何体如图所示,则它的俯视图是( )
A. B. C. D.
【答案】D
【解答】解:俯视图有3列,从左到右小正方形的个数是2,1,1,
故选:D.
2.(2023 扬州)下列图形是棱锥侧面展开图的是( )
A. B.
C. D.
【答案】D
【解答】解:四棱锥的侧面展开图是四个三角形.
故选:D.
3.(2023 淮安)如图是一个几何体的三视图,则该几何体的侧面积是( )
A.12π B.15π C.18π D.24π
【答案】B
【解答】解:由三视图可知此几何体为圆锥,
∵d=6,h=4,
∴圆锥的母线长为=5,
∴圆锥的侧面积为:×6π×5=15π,
故选:B.
4.(2023 常州)运动场上的颁奖台如图所示,它的主视图是( )
A.
B.
C.
D.
【答案】A
【解答】解:从正面看得到.
故选:A.
5.(2023 南通)如图所示的四个几何体中,俯视图是三角形的是( )
A.三棱柱 B.圆柱
C.四棱锥 D.圆锥
【答案】A
【解答】解:A.三棱柱的俯视图是三角形,故此选项符合题意;
B.圆柱体的俯视图是圆,故此选项不合题意;
C.四棱锥的俯视图是四边形(画有对角线),故此选项不合题意;
D.圆锥体的俯视图是圆(带圆心),故此选项不合题意.
故选:A.
6.(2023 苏州)今天是父亲节,小东同学准备送给父亲一个小礼物.已知礼物外包装的主视图如图所示,则该礼物的外包装不可能是( )
A.长方体 B.正方体 C.圆柱 D.三棱锥
【答案】D
【解答】解:根据主视图可知,只有D选项不可能.
故选:D.
7.(2023 连云港)如图,甲是由一条直径、一条弦及一段圆弧所围成的图形;乙是由两条半径与一段圆弧所围成的图形;丙是由不过圆心O的两条线段与一段圆弧所围成的图形.下列叙述正确的是( )
A.只有甲是扇形 B.只有乙是扇形
C.只有丙是扇形 D.只有乙、丙是扇形
【答案】B
【解答】解:由扇形的定义可知,只有乙是扇形,
故选:B.
8.(2023 连云港)下列水平放置的几何体中,主视图是圆形的是( )
A. B.
C. D.
【答案】C
【解答】解:A.主视图是三角形,故此选项不符合题意;
B.主视图是梯形,故此选项不合题意;
C.主视图是圆,故此选项符合题意;
D.主视图是矩形,故此选项不合题意;
故选:C.
9.(2022 泰州)如图为一个几何体的表面展开图,则该几何体是( )
A.三棱锥 B.四棱锥 C.四棱柱 D.圆锥
【答案】B
【解答】解:根据展开图可以得出是四棱锥的展开图,
故选:B.
10.(2022 徐州)如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A. B.
C. D.
【答案】D
【解答】解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,
A、1点6点是相对面,3点与5点是相对面,2点与4点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
B、4点与3点是相对面,2点与6点是相对面,1点与5点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
C、3点与4点是相对面,2点与6点是相对面,1点与5点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
D、2点与5点是相对面,3点与4点是相对面,1点与6点是相对面,所以可以折成符合规则的骰子,故本选项符合题意.
故选:D.
11.(2022 常州)下列图形中,为圆柱的侧面展开图的是( )
A. B.
C. D.
【答案】D
【解答】解:根据题意,把圆柱的侧面沿它的一条母线剪开展在一个平面上,
得到其侧面展开图是对边平行且相等的四边形;
又有母线垂直于上下底面,故可得是长方形.
故选:D.
12.(2022 宿迁)下列展开图中,是正方体展开图的是( )
A. B.
C. D.
【答案】C
【解答】解:由展开图的知识可知,四个小正方形绝对不可能展开成田字形,故A选项和D选项都不符合题意;
四个连成一排的小正方形可以围成前后左右四面,剩下的两面必须分在上下两面才能围成正方体,
故B选项不符合题意,C选项符合题意,
故选:C.
13.(2022 扬州)如图是某一几何体的主视图、左视图、俯视图,该几何体是( )
A.四棱柱 B.四棱锥 C.三棱柱 D.三棱锥
【答案】B
【解答】解:由于主视图与左视图是三角形,
俯视图是正方形,故该几何体是四棱锥,
故选:B.
14.(2022 南通)如图是由5个相同的正方体搭成的立体图形,则它的主视图为( )
A. B. C. D.
【答案】A
【解答】解:从正面看该组合体,所看到的图形与选项A中的图形相同,
故选:A.
15.(2022 盐城)正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( )
A.强 B.富 C.美 D.高
【答案】D
【解答】解:正方体的表面展开图相对的面之间一定相隔一个正方形,
“盐”与“高”是相对面,
“城”与“富”是相对面,
“强”与“美”是相对面,
故选:D.
16.(2021 扬州)把如图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )
A.五棱锥 B.五棱柱 C.六棱锥 D.六棱柱
【答案】A
【解答】解:由图可知:折叠后,该几何体的底面是五边形,
则该几何体为五棱锥,
故选:A.
17.(2021 盐城)如图是由4个小正方形体组合成的几何体,该几何体的主视图是( )
A. B.
C. D.
【答案】A
【解答】解:该组合体的主视图如下:
故选:A.
18.(2021 淮安)如图所示的几何体的俯视图是( )
A. B. C. D.
【答案】A
【解答】解:从上面看该几何体,所看到的图形如下:
故选:A.
19.(2021 镇江)如图所示,该几何体的俯视图是( )
A.正方形 B.长方形 C.三角形 D.圆
【答案】C
【解答】解:从上面看该几何体,所看到的图形是三角形.
故选:C.
20.(2021 泰州)如图所示几何体的左视图是( )
A. B.
C. D.
【答案】C
【解答】解:从左边看,是一列两个矩形.
故选:C.
21.(2021 南通)如图,根据三视图,这个立体图形的名称是( )
A.三棱柱 B.圆柱 C.三棱锥 D.圆锥
【答案】A
【解答】解:根据三视图可以得出立体图形是三棱柱,
故选:A.
22.(2021 苏州)如图,圆锥的主视图是( )
A. B.
C. D.
【答案】A
【解答】解:圆锥的主视图是一个等腰三角形,
故选:A.
23.(2021 常州)如图是某几何体的三视图,该几何体是( )
A.正方体 B.圆锥 C.圆柱 D.球
【答案】D
【解答】解:一个几何体的三视图都是圆,这个几何体是球.
故选:D.
二.填空题(共2小题)
24.(2023 常州)若圆柱的底面半径和高均为a,则它的体积是 πa3 (用含a的代数式表示).
【答案】πa3.
【解答】解:圆柱的底面半径和高均为a,则它的体积是πa2 a=πa3.
故答案为:πa3.
25.(2023 无锡)若直三棱柱的上下底面为正三角形,侧面展开图是边长为6的正方形,则该直三棱柱的表面积为 36+2 .
【答案】36.
【解答】解:依题意可知:直三棱柱的上下底面的正三角形的边长为2,
∴其2个底面积为=2.
∵侧面展开图是边长为6的正方形,
∴其侧面积为6×6=36,
∴该直三棱柱的表面积为36+2.
故答案为:36+2.
三.解答题(共1小题)
26.(2023 徐州)两汉文化看徐州,桐桐在徐州博物馆“天工汉玉”展厅参观时了解到;玉壁,玉环为我国的传统玉器,通常为正中带圆孔的扁圆型器物,据《尔雅 释器》记载:“肉倍好,谓之璧;肉好若一,调之环.”如图1,“肉”指边(阴影部分),“好”指孔,其比例关系见图示,以考古发现来看,这两种玉器的“肉”与“好”未必符合该比例关系.
(1)若图1中两个大圆的直径相等,则璧与环的“肉”的面积之比为 32:27 ;
(2)利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法):
①图2为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图,试判断该件玉器的比例关系是否符合“肉好若一”?
②图3表示一件圆形玉坯,若将其加工成玉璧,且比例关系符合“肉倍好”,请画出内孔.
【答案】(1)32:27;
(2)①见解析部分;
②见解析部分.
【解答】解:(1)由图1可知:璧的“肉”的面积为 π×(32﹣12)=8π;环的“肉”的面积为 π×(32﹣1.52)=6.75π,
∴它们的面积之比为 8 π:6.75 π=32:27;
故答案为32:27;
(2)①观察图象可知,不符合“肉好若一”关系;
②按照①中作出圆的圆心O,过圆心画一条直径AB,过点A作一条射线,然后以A为圆心,适当长为半 径画弧,把射线三等分,交点分别为C、D、E,连接BE,然后分别过点C、D作BE的平行线,交AB于 点F、G,进而以FG为直径画圆,则问题得解;如图所示:
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
