第6章 平面图形的认识(一)(中考常考题)江苏省2023-2024学年上学期苏科版七年级数学单元培优专题练习(含解析)
文档属性
| 名称 | 第6章 平面图形的认识(一)(中考常考题)江苏省2023-2024学年上学期苏科版七年级数学单元培优专题练习(含解析) | 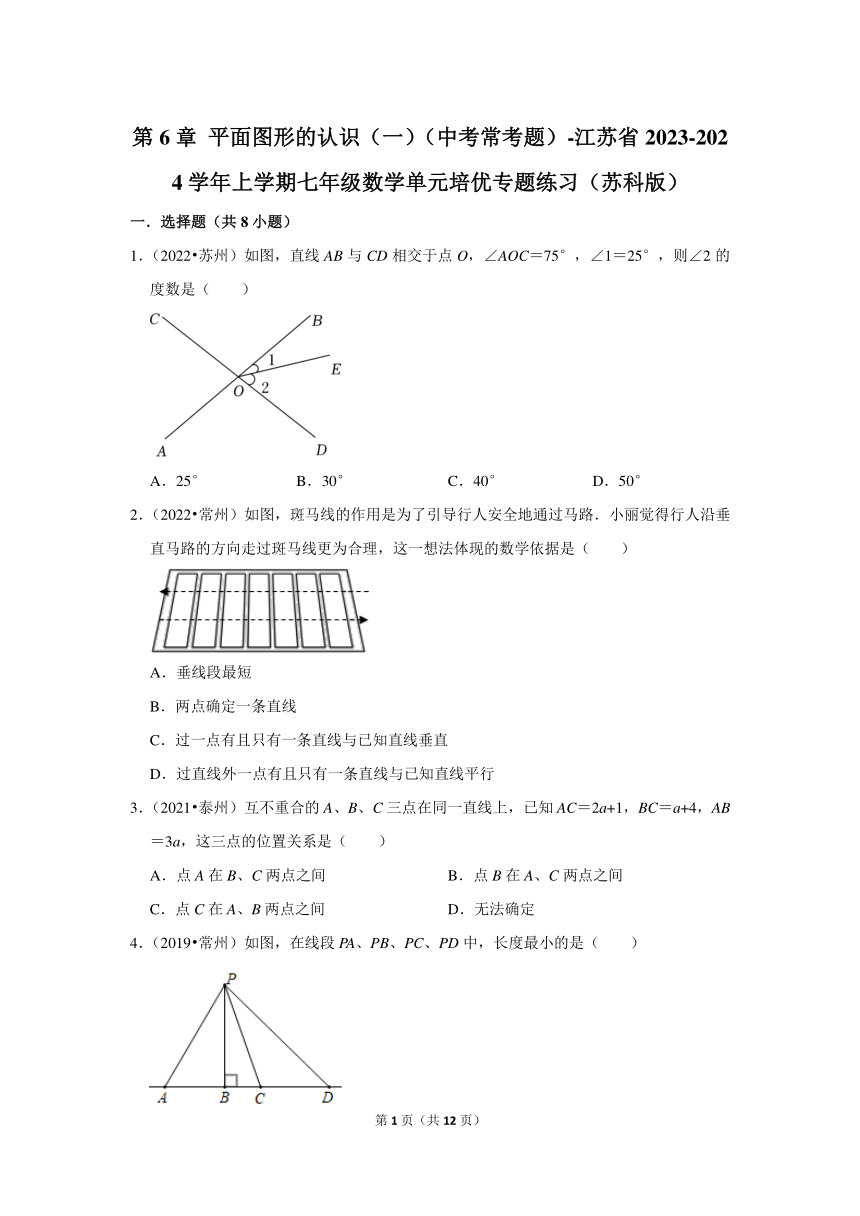 | |
| 格式 | Doc | ||
| 文件大小 | 157.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 16:47:19 | ||
图片预览




文档简介
第6章 平面图形的认识(一)(中考常考题)-江苏省2023-2024学年上学期七年级数学单元培优专题练习(苏科版)
一.选择题(共8小题)
1.(2022 苏州)如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是( )
A.25° B.30° C.40° D.50°
2.(2022 常州)如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
3.(2021 泰州)互不重合的A、B、C三点在同一直线上,已知AC=2a+1,BC=a+4,AB=3a,这三点的位置关系是( )
A.点A在B、C两点之间 B.点B在A、C两点之间
C.点C在A、B两点之间 D.无法确定
4.(2019 常州)如图,在线段PA、PB、PC、PD中,长度最小的是( )
A.线段PA B.线段PB C.线段PC D.线段PD
5.(2016 常州)已知△ABC中,BC=6,AC=3,CP⊥AB,垂足为P,则CP的长可能是( )
A.2 B.4 C.5 D.7
6.(2014 徐州)点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于( )
A.3 B.2 C.3或5 D.2或6
7.(2014 苏州)已知∠α和∠β是对顶角,若∠α=30°,则∠β的度数为( )
A.30° B.60° C.70° D.150°
8.(2012 南通)已知∠a=32°,则∠a的补角为( )
A.58° B.68° C.148° D.168°
二.填空题(共9小题)
9.(2022 连云港)已知∠A的补角为60°,则∠A= °.
10.(2019 常州)如果∠α=35°,那么∠α的余角等于 °.
11.(2016 南通)已知:如图直线AB与CD相交于点O,OE⊥AB,∠COE=60°,则∠BOD等于 度.
12.(2013 南通)如图,直线AB,CD相交于点O,OE⊥AB,∠BOD=20°,则∠COE等于 度.
13.(2013 徐州)若∠α=50°,则它的余角是 °.
14.(2013 淮安)如图,三角板的直角顶点在直线l上,若∠1=40°,则∠2的度数是 .
15.(2012 泰州)已知∠α的补角是130°,则∠α= 度.
16.(2012 扬州)一个锐角是38度,则它的余角是 度.
17.(2012 徐州)∠α=80°,则α的补角为 °.
三.解答题(共1小题)
18.(2016 南京)用两种方法证明“三角形的外角和等于360°”.
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证∠BAE+∠CBF+∠ACD=360°.
证法1:∵ ,
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵ ,
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.
第6章 平面图形的认识(一)(中考常考题)-江苏省2023-2024学年上学期七年级数学单元培优专题练习(苏科版)
参考答案与试题解析
一.选择题(共8小题)
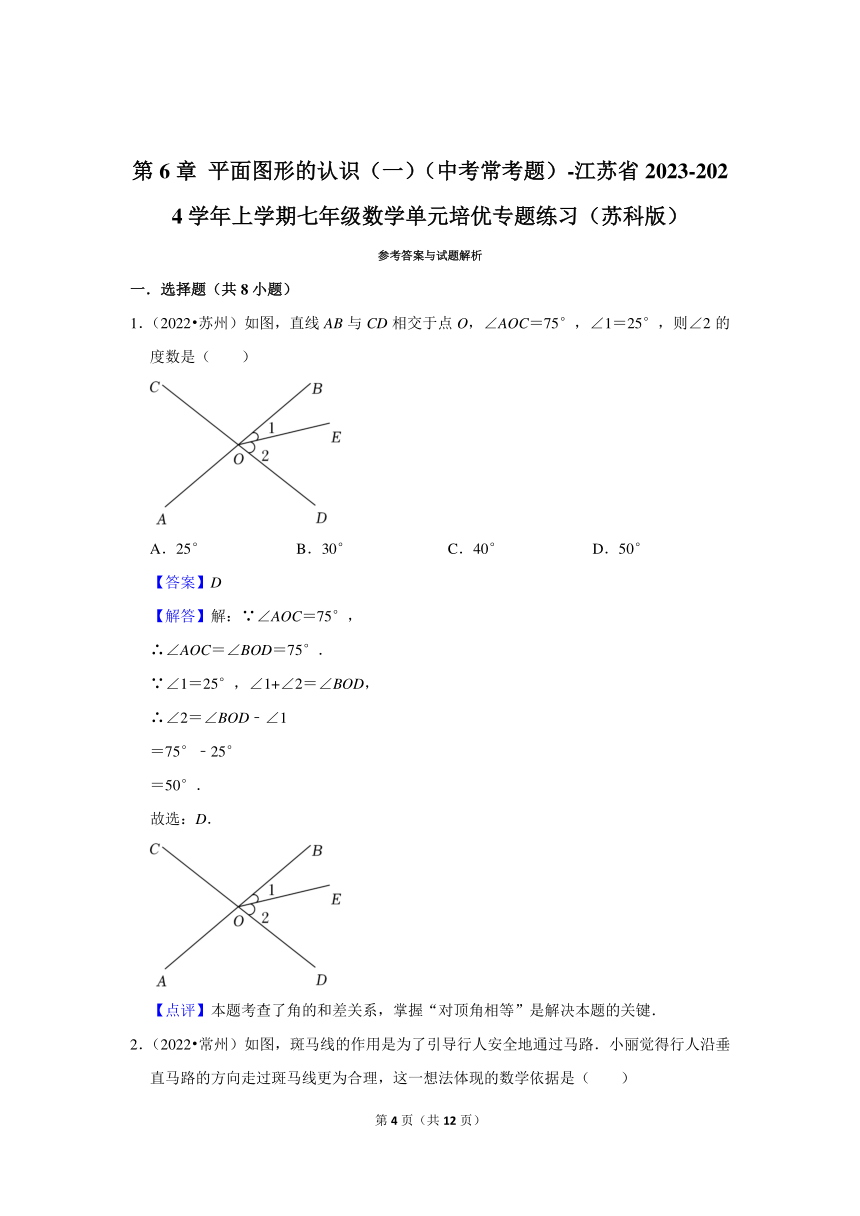
1.(2022 苏州)如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是( )
A.25° B.30° C.40° D.50°
【答案】D
【解答】解:∵∠AOC=75°,
∴∠AOC=∠BOD=75°.
∵∠1=25°,∠1+∠2=∠BOD,
∴∠2=∠BOD﹣∠1
=75°﹣25°
=50°.
故选:D.
【点评】本题考查了角的和差关系,掌握“对顶角相等”是解决本题的关键.
2.(2022 常州)如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
【答案】见试题解答内容
【解答】解:小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是垂线段最短,
故选:A.
【点评】本题主要考查了垂线段最短的性质,熟练掌握数学和生活密不可分的关系是解答本题的关键.
3.(2021 泰州)互不重合的A、B、C三点在同一直线上,已知AC=2a+1,BC=a+4,AB=3a,这三点的位置关系是( )
A.点A在B、C两点之间 B.点B在A、C两点之间
C.点C在A、B两点之间 D.无法确定
【答案】A
【解答】解:∵AC=2a+1,BC=a+4,AB=3a,A、B、C三点互不重合
∴a>0,
若点A在B、C之间,
则AB+AC=BC,
即2a+1+3a=a+4,
解得a=,
故A情况存在,
若点B在A、C之间,
则BC+AB=AC,
即a+4+3a=2a+1,
解得a=﹣,
故B情况不存在,
若点C在A、B之间,
则BC+AC=AB,
即a+4+2a+1=3a,
此时无解,
故C情况不存在,
∵互不重合的A、B、C三点在同一直线上,
故选:A.
【点评】本题主要考查两点间的距离及整式的加减,分类讨论和反证法的应用是解题的关键.
4.(2019 常州)如图,在线段PA、PB、PC、PD中,长度最小的是( )
A.线段PA B.线段PB C.线段PC D.线段PD
【答案】B
【解答】解:由直线外一点到直线上所有点的连线中,垂线段最短,可知答案为B.
故选:B.
【点评】本题考查的是直线外一点到直线上所有点的连线中,垂线段最短,这属于基本的性质定理,属于简单题.
5.(2016 常州)已知△ABC中,BC=6,AC=3,CP⊥AB,垂足为P,则CP的长可能是( )
A.2 B.4 C.5 D.7
【答案】A
【解答】解:如图,根据垂线段最短可知:PC≤3,
∴CP的长可能是2,
故选:A.
【点评】本题考查了垂线段最短的性质,正确理解此性质,垂线段最短,指的是从直线外一点到这条直线所作的垂线段最短;本题是指点C到直线AB连接的所有线段中,CP是垂线段,所以最短;在实际问题中涉及线路最短问题时,其理论依据应从“两点之间,线段最短”和“垂线段最短”这两个中去选择.
6.(2014 徐州)点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于( )
A.3 B.2 C.3或5 D.2或6
【答案】D
【解答】解:此题画图时会出现两种情况,即点C在线段AB内,点C在线段AB外,所以要分两种情况计算.
点A、B表示的数分别为﹣3、1,
AB=4.
第一种情况:在线段AB外,
AC=4+2=6;
第二种情况:在线段AB内,
AC=4﹣2=2.
故选:D.
【点评】在未画图类问题中,正确画图很重要.本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.
7.(2014 苏州)已知∠α和∠β是对顶角,若∠α=30°,则∠β的度数为( )
A.30° B.60° C.70° D.150°
【答案】A
【解答】解:∵∠α和∠β是对顶角,∠α=30°,
∴根据对顶角相等可得∠β=∠α=30°.
故选:A.
【点评】本题主要考查了对顶角相等的性质,比较简单.
8.(2012 南通)已知∠a=32°,则∠a的补角为( )
A.58° B.68° C.148° D.168°
【答案】C
【解答】解:∵∠a=32°,
∴∠a的补角为180°﹣32°=148°.
故选:C.
【点评】本题考查了余角与补角的定义,熟记互为补角的和等于180°是解题的关键.
二.填空题(共9小题)
9.(2022 连云港)已知∠A的补角为60°,则∠A= 120 °.
【答案】120.
【解答】解:∵∠A的补角为60°,
∴∠A=180°﹣60°=120°,
故答案为:120.
【点评】本题考查了余角和补角,掌握如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角是解题的关键.
10.(2019 常州)如果∠α=35°,那么∠α的余角等于 55 °.
【答案】见试题解答内容
【解答】解:∵∠α=35°,
∴∠α的余角等于90°﹣35°=55°
故答案为:55.
【点评】本题考查的两角互余的基本概念,题目属于基础概念题,比较简单.
11.(2016 南通)已知:如图直线AB与CD相交于点O,OE⊥AB,∠COE=60°,则∠BOD等于 30 度.
【答案】见试题解答内容
【解答】解:由垂线的定义,得
∠AOE=90°,
由余角的性质,得
∠AOC=∠AOE﹣∠COE=30°,
由对顶角相等,得
∠BOD=∠AOC=30°,
故答案为:30.
【点评】本题考查了垂线,利用了垂线的定义,余角的性质,对顶角的性质.
12.(2013 南通)如图,直线AB,CD相交于点O,OE⊥AB,∠BOD=20°,则∠COE等于 70 度.
【答案】见试题解答内容
【解答】解:∵∠BOD=20°,
∴∠AOC=∠BOD=20°,
∵OE⊥AB,
∴∠AOE=90°,
∴∠COE=90°﹣20°=70°,
故答案为:70.
【点评】本题考查了垂直定义,对顶角的应用,关键是求出∠AOE和∠AOC的大小.
13.(2013 徐州)若∠α=50°,则它的余角是 40 °.
【答案】见试题解答内容
【解答】解:∵∠α=50°,
∴它的余角是90°﹣50°=40°.
故答案为:40.
【点评】本题考查了余角的定义,是基础题,熟记互为余角的两个角的和等于90°是解题的关键.
14.(2013 淮安)如图,三角板的直角顶点在直线l上,若∠1=40°,则∠2的度数是 50° .
【答案】见试题解答内容
【解答】解:如图,三角板的直角顶点在直线l上,
则∠1+∠2=180°﹣90°=90°,
∵∠1=40°,
∴∠2=50°.
故答案为50°.
【点评】本题考查了余角及平角的定义,正确观察图形,得出∠1与∠2互余是解题的关键.
15.(2012 泰州)已知∠α的补角是130°,则∠α= 50 度.
【答案】见试题解答内容
【解答】解:∵∠α的补角是130°,
∴∠α=180°﹣130°=50°.
故答案为:50.
【点评】本题考查了余角与补角的定义,熟记补角的和等于180°是解题的关键.
16.(2012 扬州)一个锐角是38度,则它的余角是 52 度.
【答案】见试题解答内容
【解答】解:这个角的余角为:90°﹣38°=52°.
故答案为:52.
【点评】此题考查了余角的知识,掌握互为余角的两角之和为90°是解答本题的关键.
17.(2012 徐州)∠α=80°,则α的补角为 100 °.
【答案】见试题解答内容
【解答】解:∵∠α=80°,
∴∠α的补角的度数=180°﹣80°=100°.
故答案为:100.
【点评】本题考查了补角的定义,互补是反映了两个角之间的关系,即和是180°.
三.解答题(共1小题)
18.(2016 南京)用两种方法证明“三角形的外角和等于360°”.
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证∠BAE+∠CBF+∠ACD=360°.
证法1:∵ 平角等于180° ,
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵ ∠1+∠2+∠3=180° ,
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.
【答案】见试题解答内容
【解答】证明:证法1:∵平角等于180°,
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵∠1+∠2+∠3=180°,
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
证法2:∵∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2,
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3),
∵∠1+∠2+∠3=180°,
∴∠BAE+∠CBF+∠ACD=360°.
故答案为:平角等于180°,∠1+∠2+∠3=180°.
【点评】本题考查了多边形的外角和:n边形的外角和为360°.也考查了三角形内角和定理和外角性质,平行线的性质.
第1页(共1页)
一.选择题(共8小题)
1.(2022 苏州)如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是( )
A.25° B.30° C.40° D.50°
2.(2022 常州)如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
3.(2021 泰州)互不重合的A、B、C三点在同一直线上,已知AC=2a+1,BC=a+4,AB=3a,这三点的位置关系是( )
A.点A在B、C两点之间 B.点B在A、C两点之间
C.点C在A、B两点之间 D.无法确定
4.(2019 常州)如图,在线段PA、PB、PC、PD中,长度最小的是( )
A.线段PA B.线段PB C.线段PC D.线段PD
5.(2016 常州)已知△ABC中,BC=6,AC=3,CP⊥AB,垂足为P,则CP的长可能是( )
A.2 B.4 C.5 D.7
6.(2014 徐州)点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于( )
A.3 B.2 C.3或5 D.2或6
7.(2014 苏州)已知∠α和∠β是对顶角,若∠α=30°,则∠β的度数为( )
A.30° B.60° C.70° D.150°
8.(2012 南通)已知∠a=32°,则∠a的补角为( )
A.58° B.68° C.148° D.168°
二.填空题(共9小题)
9.(2022 连云港)已知∠A的补角为60°,则∠A= °.
10.(2019 常州)如果∠α=35°,那么∠α的余角等于 °.
11.(2016 南通)已知:如图直线AB与CD相交于点O,OE⊥AB,∠COE=60°,则∠BOD等于 度.
12.(2013 南通)如图,直线AB,CD相交于点O,OE⊥AB,∠BOD=20°,则∠COE等于 度.
13.(2013 徐州)若∠α=50°,则它的余角是 °.
14.(2013 淮安)如图,三角板的直角顶点在直线l上,若∠1=40°,则∠2的度数是 .
15.(2012 泰州)已知∠α的补角是130°,则∠α= 度.
16.(2012 扬州)一个锐角是38度,则它的余角是 度.
17.(2012 徐州)∠α=80°,则α的补角为 °.
三.解答题(共1小题)
18.(2016 南京)用两种方法证明“三角形的外角和等于360°”.
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证∠BAE+∠CBF+∠ACD=360°.
证法1:∵ ,
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵ ,
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.
第6章 平面图形的认识(一)(中考常考题)-江苏省2023-2024学年上学期七年级数学单元培优专题练习(苏科版)
参考答案与试题解析
一.选择题(共8小题)
1.(2022 苏州)如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是( )
A.25° B.30° C.40° D.50°
【答案】D
【解答】解:∵∠AOC=75°,
∴∠AOC=∠BOD=75°.
∵∠1=25°,∠1+∠2=∠BOD,
∴∠2=∠BOD﹣∠1
=75°﹣25°
=50°.
故选:D.
【点评】本题考查了角的和差关系,掌握“对顶角相等”是解决本题的关键.
2.(2022 常州)如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
【答案】见试题解答内容
【解答】解:小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是垂线段最短,
故选:A.
【点评】本题主要考查了垂线段最短的性质,熟练掌握数学和生活密不可分的关系是解答本题的关键.
3.(2021 泰州)互不重合的A、B、C三点在同一直线上,已知AC=2a+1,BC=a+4,AB=3a,这三点的位置关系是( )
A.点A在B、C两点之间 B.点B在A、C两点之间
C.点C在A、B两点之间 D.无法确定
【答案】A
【解答】解:∵AC=2a+1,BC=a+4,AB=3a,A、B、C三点互不重合
∴a>0,
若点A在B、C之间,
则AB+AC=BC,
即2a+1+3a=a+4,
解得a=,
故A情况存在,
若点B在A、C之间,
则BC+AB=AC,
即a+4+3a=2a+1,
解得a=﹣,
故B情况不存在,
若点C在A、B之间,
则BC+AC=AB,
即a+4+2a+1=3a,
此时无解,
故C情况不存在,
∵互不重合的A、B、C三点在同一直线上,
故选:A.
【点评】本题主要考查两点间的距离及整式的加减,分类讨论和反证法的应用是解题的关键.
4.(2019 常州)如图,在线段PA、PB、PC、PD中,长度最小的是( )
A.线段PA B.线段PB C.线段PC D.线段PD
【答案】B
【解答】解:由直线外一点到直线上所有点的连线中,垂线段最短,可知答案为B.
故选:B.
【点评】本题考查的是直线外一点到直线上所有点的连线中,垂线段最短,这属于基本的性质定理,属于简单题.
5.(2016 常州)已知△ABC中,BC=6,AC=3,CP⊥AB,垂足为P,则CP的长可能是( )
A.2 B.4 C.5 D.7
【答案】A
【解答】解:如图,根据垂线段最短可知:PC≤3,
∴CP的长可能是2,
故选:A.
【点评】本题考查了垂线段最短的性质,正确理解此性质,垂线段最短,指的是从直线外一点到这条直线所作的垂线段最短;本题是指点C到直线AB连接的所有线段中,CP是垂线段,所以最短;在实际问题中涉及线路最短问题时,其理论依据应从“两点之间,线段最短”和“垂线段最短”这两个中去选择.
6.(2014 徐州)点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于( )
A.3 B.2 C.3或5 D.2或6
【答案】D
【解答】解:此题画图时会出现两种情况,即点C在线段AB内,点C在线段AB外,所以要分两种情况计算.
点A、B表示的数分别为﹣3、1,
AB=4.
第一种情况:在线段AB外,
AC=4+2=6;
第二种情况:在线段AB内,
AC=4﹣2=2.
故选:D.
【点评】在未画图类问题中,正确画图很重要.本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.
7.(2014 苏州)已知∠α和∠β是对顶角,若∠α=30°,则∠β的度数为( )
A.30° B.60° C.70° D.150°
【答案】A
【解答】解:∵∠α和∠β是对顶角,∠α=30°,
∴根据对顶角相等可得∠β=∠α=30°.
故选:A.
【点评】本题主要考查了对顶角相等的性质,比较简单.
8.(2012 南通)已知∠a=32°,则∠a的补角为( )
A.58° B.68° C.148° D.168°
【答案】C
【解答】解:∵∠a=32°,
∴∠a的补角为180°﹣32°=148°.
故选:C.
【点评】本题考查了余角与补角的定义,熟记互为补角的和等于180°是解题的关键.
二.填空题(共9小题)
9.(2022 连云港)已知∠A的补角为60°,则∠A= 120 °.
【答案】120.
【解答】解:∵∠A的补角为60°,
∴∠A=180°﹣60°=120°,
故答案为:120.
【点评】本题考查了余角和补角,掌握如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角是解题的关键.
10.(2019 常州)如果∠α=35°,那么∠α的余角等于 55 °.
【答案】见试题解答内容
【解答】解:∵∠α=35°,
∴∠α的余角等于90°﹣35°=55°
故答案为:55.
【点评】本题考查的两角互余的基本概念,题目属于基础概念题,比较简单.
11.(2016 南通)已知:如图直线AB与CD相交于点O,OE⊥AB,∠COE=60°,则∠BOD等于 30 度.
【答案】见试题解答内容
【解答】解:由垂线的定义,得
∠AOE=90°,
由余角的性质,得
∠AOC=∠AOE﹣∠COE=30°,
由对顶角相等,得
∠BOD=∠AOC=30°,
故答案为:30.
【点评】本题考查了垂线,利用了垂线的定义,余角的性质,对顶角的性质.
12.(2013 南通)如图,直线AB,CD相交于点O,OE⊥AB,∠BOD=20°,则∠COE等于 70 度.
【答案】见试题解答内容
【解答】解:∵∠BOD=20°,
∴∠AOC=∠BOD=20°,
∵OE⊥AB,
∴∠AOE=90°,
∴∠COE=90°﹣20°=70°,
故答案为:70.
【点评】本题考查了垂直定义,对顶角的应用,关键是求出∠AOE和∠AOC的大小.
13.(2013 徐州)若∠α=50°,则它的余角是 40 °.
【答案】见试题解答内容
【解答】解:∵∠α=50°,
∴它的余角是90°﹣50°=40°.
故答案为:40.
【点评】本题考查了余角的定义,是基础题,熟记互为余角的两个角的和等于90°是解题的关键.
14.(2013 淮安)如图,三角板的直角顶点在直线l上,若∠1=40°,则∠2的度数是 50° .
【答案】见试题解答内容
【解答】解:如图,三角板的直角顶点在直线l上,
则∠1+∠2=180°﹣90°=90°,
∵∠1=40°,
∴∠2=50°.
故答案为50°.
【点评】本题考查了余角及平角的定义,正确观察图形,得出∠1与∠2互余是解题的关键.
15.(2012 泰州)已知∠α的补角是130°,则∠α= 50 度.
【答案】见试题解答内容
【解答】解:∵∠α的补角是130°,
∴∠α=180°﹣130°=50°.
故答案为:50.
【点评】本题考查了余角与补角的定义,熟记补角的和等于180°是解题的关键.
16.(2012 扬州)一个锐角是38度,则它的余角是 52 度.
【答案】见试题解答内容
【解答】解:这个角的余角为:90°﹣38°=52°.
故答案为:52.
【点评】此题考查了余角的知识,掌握互为余角的两角之和为90°是解答本题的关键.
17.(2012 徐州)∠α=80°,则α的补角为 100 °.
【答案】见试题解答内容
【解答】解:∵∠α=80°,
∴∠α的补角的度数=180°﹣80°=100°.
故答案为:100.
【点评】本题考查了补角的定义,互补是反映了两个角之间的关系,即和是180°.
三.解答题(共1小题)
18.(2016 南京)用两种方法证明“三角形的外角和等于360°”.
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证∠BAE+∠CBF+∠ACD=360°.
证法1:∵ 平角等于180° ,
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵ ∠1+∠2+∠3=180° ,
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.
【答案】见试题解答内容
【解答】证明:证法1:∵平角等于180°,
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵∠1+∠2+∠3=180°,
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
证法2:∵∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2,
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3),
∵∠1+∠2+∠3=180°,
∴∠BAE+∠CBF+∠ACD=360°.
故答案为:平角等于180°,∠1+∠2+∠3=180°.
【点评】本题考查了多边形的外角和:n边形的外角和为360°.也考查了三角形内角和定理和外角性质,平行线的性质.
第1页(共1页)
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
