2.9.2有理数的乘法

课件25张PPT。义务教育课程标准试验教科书七年级 上册华东师范大学出版社2.9有理数的乘法（第二课时）教学目标1．使学生掌握有理数乘法的运算律，并利用运算律简化乘法运算。
2．使学生掌握多个有理数相乘的积的符号法则。
3．培养学生观察、归纳、概括及运算能力。教学重点、难点重点：乘法的符号法则和乘法的运算
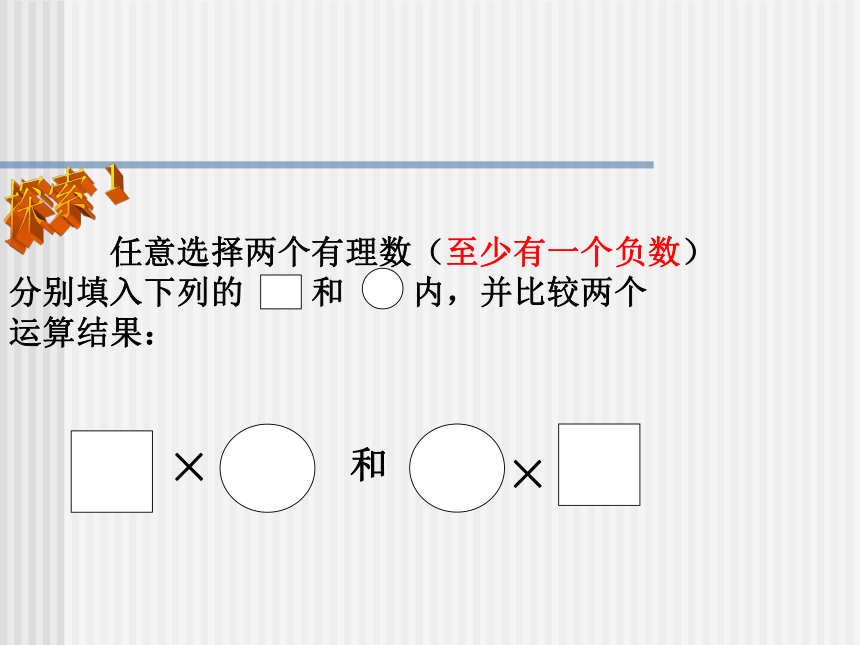
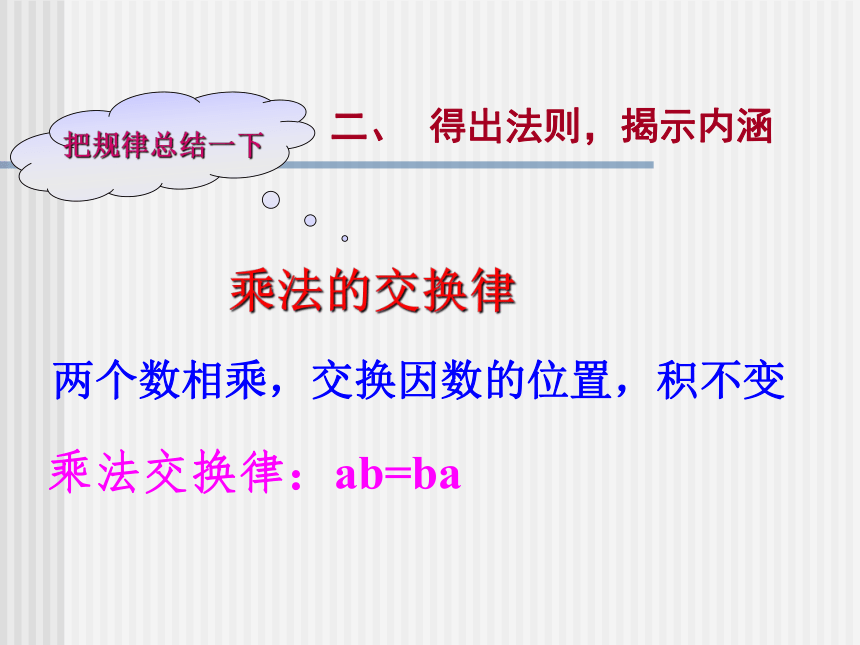
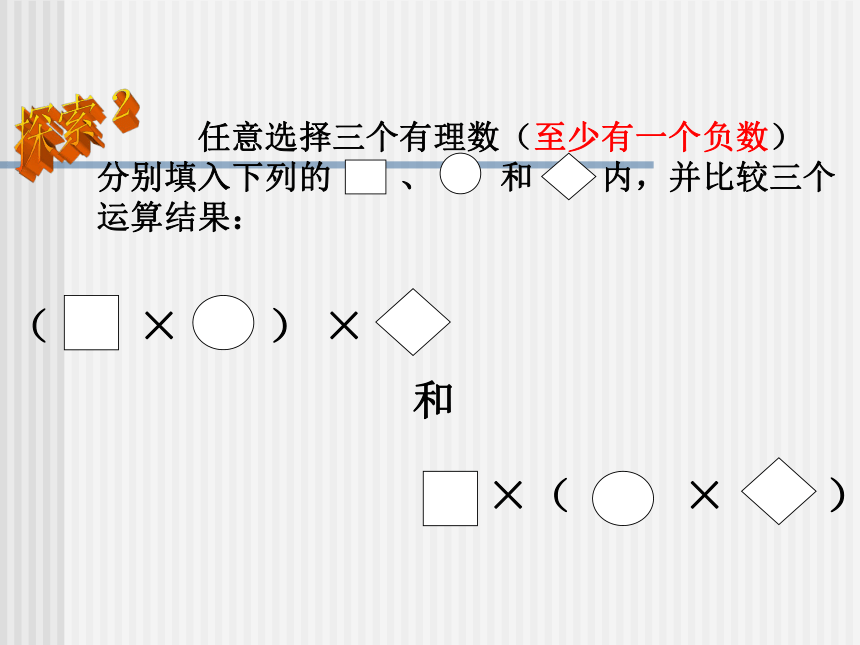
难点：积的符号的确定。 一、温故知新、引入课题叙述有理数乘法法则。?探索１?? (6)(-10)×(-16)；(1)(-6) ×5；(2)(-9)×(-4);(3)(-36)×(-1);(4) 3×(-11); (5)(-5) ×16; (7)100 ×(-0.001); (8)-30×0.2 ；-90-3336-80-0.1-616036通过计算发现了什么呢？两个数相乘，交换因数的位置，积不变乘法交换律：ab=ba乘法的交换律二、??得出法则，揭示内涵探索２　　　任意选择三个有理数（至少有一个负数）
分别填入下列的　　、　　和　　内，并比较三个
运算结果：（　　×　　） ×　　　×（ 　 　×　 　）和
(1)［3×(―4)］×(―5)；

(2) 3×［(―4)×(―5)］；=（-12）×（-5）
= 60=3×20
=60三个有理数相乘，先把前两个数相乘， 或者先把后两个数相乘，积不变。乘法结合律：（ab)c=a(bc)乘法的结合律根据乘法交换律和结合律可以推出：
三个以上有理数相乘，可以任意交换因数的位置，也可先把其中的几个数相乘三、强化法则，深入理解例1.计算分析：一、三和二、四项结合起来运算解：四 例题示范，初步运用试直接写出下列各式的结果：60-6060观察以上各式，能发现几个正数与负数相乘，积的符号与各因数的符号之间的关系：一般地，我们有:几个不等于0的数相乘，积的符号由负因数的个数决定，当负因数有
奇数个时，积为负；当负因数有偶数个时，积为正.
几个不等于0的数相乘，首先确定积的符号，然后把绝对值相乘.几个数相乘，有一个因数为0，积就为0.例2 计算四 例题示范，初步运用（1）＝８＋３＝１１解：原式解：原式＝０（2）（3）解：原式＝（一）下列各式中用了哪条运算律？如何用字母表示？
1、（-4）×8=8 ×（-4）
２、[29×（-5/6）] ×（-12）=29 ×[（-5/6） ×（-12）]
３、1.25×(-4)×(-25)×8= (1.25×8)×[(-4)×(-25)]乘法交换律：ab=ba乘法结合律：(ab)c=a(bc)根据乘法交换律和结合律可以推出：三个以上有理数相乘，可以任意交换因数的位置，也可先把其中的几个数
相乘（乘法交换律和结合律）五、分层练习，形成能力（二）、为使运算简便，如何把下列算式变形？
1、（-1/20）×1.25×(-8)
２、（-10）×（-8.24) ×(-0.1)
３、(-5/6)×2.4×(3/5)
４、12×25×（-1/3）×（-1/30）
(二、三项结合起来运算）
(一、三项结合起来运算）（一、三项结合起来运算）（一、三和二、四项结合起来运算）（三）、用“>”、“<”或“=”填空。
（1）（-3）×（-5） ×（-7） ×（-9）　　0
（2）（+8.36） ×（+2.9） ×（-7.89）　　0
（3）50 ×（-2） ×（-3） ×（-2） ×（-5）　　0
（4）（-3） ×（-2） ×（-1）　　0
（5）739 ×（-123） ×（-329） ×0　　0>＜>=＜（四）.细心算一算1.2.解：厡式解:厡式1.用“＜”或“＞”号填空
（1）如果a＜0 b＞0那么 ab ＿ 0
（2）如果a＜0 b＜0那么 ab ＿ 0＜＞2.判断下列方程的解是正数、负数还是0：
（1） 4X= -16 （2）-3X=18
（3）-9X=-36 （4）-5X=03.思考题: （1）当a ＞0时，a与 2a哪个大？
（2）当a ＜ 0时，a与2a哪个大？能力拓展这节课，我的收获是---六、回顾小结，
突出重点
1.乘法的交换律
2.乘法的结合律
3.几个不等于零的有理数相乘积的符号与负因数个数的关系
4.几个数和零相乘结果仍得零1.课本P57页，习题2.9 3
2.预习课本P55—P56七、布置作业，引导预习