1.2.2 加减消元法(第1课时) 课件(共28张PPT)
文档属性
| 名称 | 1.2.2 加减消元法(第1课时) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 08:42:05 | ||
图片预览







文档简介
(共28张PPT)
1.2 二元一次方程组的解法
1.2.2 加减消元法
第1课时 用加减法解系数较简单的方程组
1.会阐述用加减法解二元一次方程组的基本思路:通过“加减”达到“消元”的目的,从而把二元一次方程组转化为一元一次方程来求解;
2.会用加减法解简单的二元一次方程组.
3.在探究的过程中,获得用加减法解二元一次方程组的初步经验.
4.培养学生观察、归纳、类比、联想以及分析问题、解决问题的能力.
【教学重点】
学会用加减法解简单的二元一次方程组.
【教学难点】
准确灵活地选择和运用加减消元法解二元一次方程组.
解二元一次方程组的基本想法是:_________________________
___________________________________________________
消去一个未知数(简称为消元),
得到一个一元一次方程,
然后解这个一元一次方程.
关键
把其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入到另一个方程中,便得到一个一元一次方程.这种解方程组的方法
叫做代入消元法.简称代入法.
1、解二元一次方程组的基本思路是什么?
基本思路:
消元: 二元
一元
2、用代入法解方程的步骤是什么?
主要步骤:
变形
代入
求解
写解
用一个未知数的代数式
表示另一个未知数
消去一个元
分别求出两个未知数的值
写出方程组的解
3x + 5y = 21, ①
2x - 5y = -11. ②
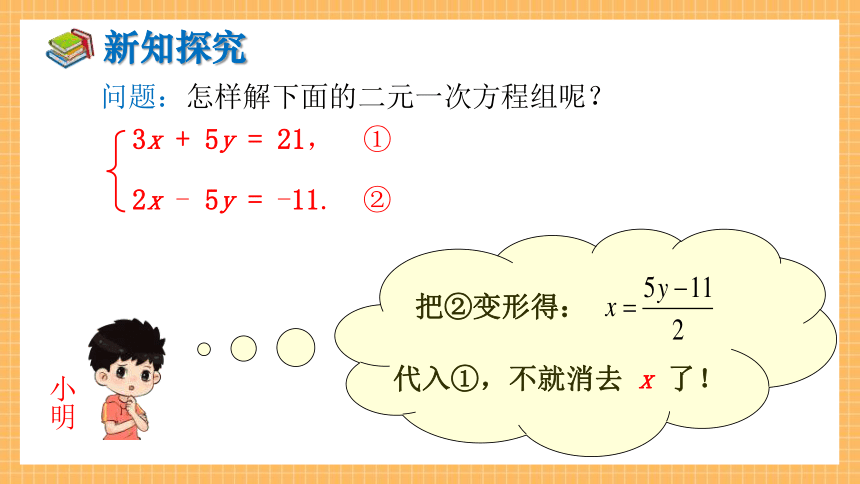
小明
把②变形得:
代入①,不就消去 x 了!
问题:怎样解下面的二元一次方程组呢?
3x + 5y = 21, ①
2x - 5y = -11. ②
问题:怎样解下面的二元一次方程组呢?
小亮
把②变形得
可以直接代入①呀!
3x + 5y = 21, ①
2x - 5y = -11. ②
问题:怎样解下面的二元一次方程组呢?
5y 和 -5y 互为相反数……
小丽
按照小丽的思路,你能消去一个未知数吗?
①
②
分析: ① + ②
①左边 + ②左边 = ①右边 + ②右边
3x + 5y + 2x-5y = 10
5x = 10
(3x + 5y)
+ (2x - 5y)
= 21
+ (-11)
小丽
5y 和-5y 互为相反数……
解方程组
解:
由 ① + ② 得
将 x = 2 代入①得
6 + 5y = 21,
解得 y = 3.
所以原方程组的解是
x = 2,
y = 3.
①
②
5x = 10,
解得 x = 2.
你学会了吗?
同一未知数的系数互为相反数时,
把两个方程的两边分别 .
相加
3x + 10y = 2.8, ①
15x - 10y = 8. ②
解:把 ① + ②得 18x = 10.8,
即 x = 0.6.
把 x = 0.6 代入 ①,得3×0.6 + 10y = 2.8.
解得 y = 0.1.
例1 解方程组
所以这个方程组的解是
x = 0.6,
y = 0.1.
例2 解下列二元一次方程组:
解:由②-①得
解得
把
代入①,得
解得
所以方程组的解为
方程①②中未知数 x 的系数相等,可以将两个方程相减消去未知数 x.
①
②
同一未知数的系数相等时,
把两个方程的两边分别 .
相减
像上面这种解二元一次方程组的方法,叫做加减消元法,简称加减法.
当方程组中两个方程的某个未知数的系数互为相反数或相等时,可以把方程的两边分别相加(系数互为相反数)或相减(系数相等)来消去这个未知数,得到一个一元一次方程,进而求得二元一次方程组的解.
例 3
解二元一次方程组:
2x+3y=﹣11, ①
6x-5y=9. ②
能直接相加减消掉一个未知数吗?
如何把同一未知数的系数变成一样呢?
②-③,得
-14y=42,
解得
y=﹣3.
把y=﹣3代入①式,得
2x+3×(﹣3)=﹣11,
解得
x=﹣1.
因此原方程组的解是
x=﹣1,
y=﹣3.
解:①×3,得
6x+9y=﹣33, ③
在例3中,如果先消去y应该如何解?会与上述结果一致吗?
2x+3y=﹣11, ①
6x-5y=9. ②
②+③,得
解得
x=﹣1.
把x=﹣1代入①式,得
2×(﹣1)+3y=﹣11,
解得
y=﹣3.
因此原方程组的解是
x=﹣1,
y=﹣3.
解:①× ,得
x+5y=﹣ ,③
x= ,
加减消元法
两个二元一次方程中
同一个未知数的系数相同 相减
同一个未知数的系数互为相反数 相加
注:若方程组中没有一个未知数的系数相同或相反,可使某个方程扩大一定的倍数,使得某个未知数的系数相同或相反,从而使用加减消元法求解。
找系数的最小公倍数
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元
加减消元:
消去一个元
分别求出两个未知数的值
写出原方程组的解
同一个未知数的系数相同或互为相反数
用加减法解二元一次方程组:
1、用加减法解二元一次方程组:
2x+y=﹣2, ①
﹣2x+3y=18;②
(1)
5a-2b=11, ①
5a+3b=﹣4;②
(2)
解:①+②,得
2x+y+(﹣2x+3y)=﹣2+18,
4y=16,
解得
y=4.
把y=4代入①式,得
2x+4=﹣2,
解得
x=﹣3.
因此原方程组的解是
x=﹣3,
y=4.
解:①-②,得
5a-2b-(5a+3b)=11-(﹣4),
﹣5b=15,
解得
b=﹣3.
把b=﹣3代入②式,得
5a+3×(﹣3)=﹣4,
解得
a=1.
因此原方程组的解是
a=1,
b=﹣3.
3m+2n=8, ①
6m-5n=﹣47; ②
(3)
2x-4y=34, ①
5x+2y=31; ②
(4)
③-②,得
9n=63,
解得
n=7.
把n=7代入①式,得
3m+2×7=8,
解得
m=﹣2.
因此原方程组的解是
m=﹣2,
n=7.
解:①×2,得
6m+4n=16, ③
③+②,得
12x=96,
解得
x=8.
把x=8代入①式,得
2×8-4y=34,
解得
因此原方程组的解是
解:②×2,得
10x+4y=62, ③
y=﹣ .
x=8,
y=﹣ .
[选自教材P10 练习]
B
2. 用加减法解方程组
6x + 7y = -19,①
6x - 5y = 17 ②
应用( )
A. ① - ② 消去 y
B. ① - ② 消去 x
C. ② - ① 消去常数项
D. 以上都不对
3.已知是二元一次方程组的解,的值
解:把代入原方程组中可以得到:
解得
∴
4. 已知 x、y 满足方程组 求代数式 x-y 的值.
解: ,
.
②-① 得 2x-2y=-1-5,
故 x-y=-3.
①
②
5、已知 则 a + b 等于____.
3
①
②
分析:方法一:直接解方程组,求出 a 与 b 的值,然后就可以求出 a + b.
方法二:① + ② 得 4a + 4b = 12,
故a + b = 3.
6.已知关于的二元一次方程组,的值。
解:得
因为关于的二元一次方程组 所以
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元
加减消元:
消去一个元
分别求出两个未知数的值
写出原方程组的解
同一个未知数的系数相同或互为相反数
用加减法解二元一次方程组:
1.教材第10页“练习”.
2.完成同步练习册中本课时的练习.
1.2 二元一次方程组的解法
1.2.2 加减消元法
第1课时 用加减法解系数较简单的方程组
1.会阐述用加减法解二元一次方程组的基本思路:通过“加减”达到“消元”的目的,从而把二元一次方程组转化为一元一次方程来求解;
2.会用加减法解简单的二元一次方程组.
3.在探究的过程中,获得用加减法解二元一次方程组的初步经验.
4.培养学生观察、归纳、类比、联想以及分析问题、解决问题的能力.
【教学重点】
学会用加减法解简单的二元一次方程组.
【教学难点】
准确灵活地选择和运用加减消元法解二元一次方程组.
解二元一次方程组的基本想法是:_________________________
___________________________________________________
消去一个未知数(简称为消元),
得到一个一元一次方程,
然后解这个一元一次方程.
关键
把其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入到另一个方程中,便得到一个一元一次方程.这种解方程组的方法
叫做代入消元法.简称代入法.
1、解二元一次方程组的基本思路是什么?
基本思路:
消元: 二元
一元
2、用代入法解方程的步骤是什么?
主要步骤:
变形
代入
求解
写解
用一个未知数的代数式
表示另一个未知数
消去一个元
分别求出两个未知数的值
写出方程组的解
3x + 5y = 21, ①
2x - 5y = -11. ②
小明
把②变形得:
代入①,不就消去 x 了!
问题:怎样解下面的二元一次方程组呢?
3x + 5y = 21, ①
2x - 5y = -11. ②
问题:怎样解下面的二元一次方程组呢?
小亮
把②变形得
可以直接代入①呀!
3x + 5y = 21, ①
2x - 5y = -11. ②
问题:怎样解下面的二元一次方程组呢?
5y 和 -5y 互为相反数……
小丽
按照小丽的思路,你能消去一个未知数吗?
①
②
分析: ① + ②
①左边 + ②左边 = ①右边 + ②右边
3x + 5y + 2x-5y = 10
5x = 10
(3x + 5y)
+ (2x - 5y)
= 21
+ (-11)
小丽
5y 和-5y 互为相反数……
解方程组
解:
由 ① + ② 得
将 x = 2 代入①得
6 + 5y = 21,
解得 y = 3.
所以原方程组的解是
x = 2,
y = 3.
①
②
5x = 10,
解得 x = 2.
你学会了吗?
同一未知数的系数互为相反数时,
把两个方程的两边分别 .
相加
3x + 10y = 2.8, ①
15x - 10y = 8. ②
解:把 ① + ②得 18x = 10.8,
即 x = 0.6.
把 x = 0.6 代入 ①,得3×0.6 + 10y = 2.8.
解得 y = 0.1.
例1 解方程组
所以这个方程组的解是
x = 0.6,
y = 0.1.
例2 解下列二元一次方程组:
解:由②-①得
解得
把
代入①,得
解得
所以方程组的解为
方程①②中未知数 x 的系数相等,可以将两个方程相减消去未知数 x.
①
②
同一未知数的系数相等时,
把两个方程的两边分别 .
相减
像上面这种解二元一次方程组的方法,叫做加减消元法,简称加减法.
当方程组中两个方程的某个未知数的系数互为相反数或相等时,可以把方程的两边分别相加(系数互为相反数)或相减(系数相等)来消去这个未知数,得到一个一元一次方程,进而求得二元一次方程组的解.
例 3
解二元一次方程组:
2x+3y=﹣11, ①
6x-5y=9. ②
能直接相加减消掉一个未知数吗?
如何把同一未知数的系数变成一样呢?
②-③,得
-14y=42,
解得
y=﹣3.
把y=﹣3代入①式,得
2x+3×(﹣3)=﹣11,
解得
x=﹣1.
因此原方程组的解是
x=﹣1,
y=﹣3.
解:①×3,得
6x+9y=﹣33, ③
在例3中,如果先消去y应该如何解?会与上述结果一致吗?
2x+3y=﹣11, ①
6x-5y=9. ②
②+③,得
解得
x=﹣1.
把x=﹣1代入①式,得
2×(﹣1)+3y=﹣11,
解得
y=﹣3.
因此原方程组的解是
x=﹣1,
y=﹣3.
解:①× ,得
x+5y=﹣ ,③
x= ,
加减消元法
两个二元一次方程中
同一个未知数的系数相同 相减
同一个未知数的系数互为相反数 相加
注:若方程组中没有一个未知数的系数相同或相反,可使某个方程扩大一定的倍数,使得某个未知数的系数相同或相反,从而使用加减消元法求解。
找系数的最小公倍数
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元
加减消元:
消去一个元
分别求出两个未知数的值
写出原方程组的解
同一个未知数的系数相同或互为相反数
用加减法解二元一次方程组:
1、用加减法解二元一次方程组:
2x+y=﹣2, ①
﹣2x+3y=18;②
(1)
5a-2b=11, ①
5a+3b=﹣4;②
(2)
解:①+②,得
2x+y+(﹣2x+3y)=﹣2+18,
4y=16,
解得
y=4.
把y=4代入①式,得
2x+4=﹣2,
解得
x=﹣3.
因此原方程组的解是
x=﹣3,
y=4.
解:①-②,得
5a-2b-(5a+3b)=11-(﹣4),
﹣5b=15,
解得
b=﹣3.
把b=﹣3代入②式,得
5a+3×(﹣3)=﹣4,
解得
a=1.
因此原方程组的解是
a=1,
b=﹣3.
3m+2n=8, ①
6m-5n=﹣47; ②
(3)
2x-4y=34, ①
5x+2y=31; ②
(4)
③-②,得
9n=63,
解得
n=7.
把n=7代入①式,得
3m+2×7=8,
解得
m=﹣2.
因此原方程组的解是
m=﹣2,
n=7.
解:①×2,得
6m+4n=16, ③
③+②,得
12x=96,
解得
x=8.
把x=8代入①式,得
2×8-4y=34,
解得
因此原方程组的解是
解:②×2,得
10x+4y=62, ③
y=﹣ .
x=8,
y=﹣ .
[选自教材P10 练习]
B
2. 用加减法解方程组
6x + 7y = -19,①
6x - 5y = 17 ②
应用( )
A. ① - ② 消去 y
B. ① - ② 消去 x
C. ② - ① 消去常数项
D. 以上都不对
3.已知是二元一次方程组的解,的值
解:把代入原方程组中可以得到:
解得
∴
4. 已知 x、y 满足方程组 求代数式 x-y 的值.
解: ,
.
②-① 得 2x-2y=-1-5,
故 x-y=-3.
①
②
5、已知 则 a + b 等于____.
3
①
②
分析:方法一:直接解方程组,求出 a 与 b 的值,然后就可以求出 a + b.
方法二:① + ② 得 4a + 4b = 12,
故a + b = 3.
6.已知关于的二元一次方程组,的值。
解:得
因为关于的二元一次方程组 所以
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元
加减消元:
消去一个元
分别求出两个未知数的值
写出原方程组的解
同一个未知数的系数相同或互为相反数
用加减法解二元一次方程组:
1.教材第10页“练习”.
2.完成同步练习册中本课时的练习.
